紫外非线性光学晶体分子设计

林哲帅,吴以成

(中国科学院理化技术研究所 中国科学院功能晶体与激光技术重点实验室，北京 100190)



紫外非线性光学晶体分子设计

林哲帅,吴以成

(中国科学院理化技术研究所 中国科学院功能晶体与激光技术重点实验室，北京 100190)

摘要：紫外非线性光学晶体对全固态激光器的发展起着举足轻重的作用,对性能优秀的紫外非线性光学晶体的探索是光电功能材料领域的研究热点。如何在种类繁多的晶体材料中高效地搜索并获得结构优化的紫外非线性光学晶体，是当前该领域研究的关键问题。对非线性光学材料构效关系研究的发展历史进行了回顾，重点介绍了阴离子基团理论以及第一性原理方法在新型紫外非线性光学材料探索中的重要应用。材料计算模拟方法不仅能够较准确地预测紫外非线性光学晶体的关键光学参数，并可以定量和直观地分析其与晶体结构特征之间的内在关系。通过将理论模拟与结构搜索、化学合成、粉末倍频效应测试、单晶生长等实验手段紧密结合，建立了快速高效的非线性光学材料分子设计专家系统。具体的科研数据及成果显示，发展和完善这一基于分子工程学基础的专家系统，将能加快非线性光学晶体的研究步伐，提升其自主创新水平。

关键词：紫外非线性光学晶体；分子设计；构效关系；阴离子基团理论与第一性原理方法

1前言

非线性光学晶体由于具有变换波长、增大振幅、开关、记忆等光电性能而成为一种重要的光电信息功能材料，被称为“光学半导体”、“激光技术的重要物质基础”。其中，性能优秀的紫外非线性光学晶体作为对当前高科技领域发展具有举足轻重作用的核心器件，成为近年来光电功能材料领域的研究热点之一[1-3]。这种光电功能晶体通过倍频或和频的方式，能够产生紫外乃至深紫外激光的输出，具有转换效率高、光束质量好、可调谐、小型化、易于操控等突出优点，已被广泛应用于全固态激光器中。在激光加工、精细能谱学、化学反应动力学、表面物理和半导体材料等科技及工业前沿领域发挥着至关重要的作用。

20世纪60年代初，随着激光技术的发展，Franken等[4]在石英晶体中发现了二阶非线性光学效应。在随后数年中，科学家仅仅认识到材料的非线性光学响应依赖于外加的光电场和材料的二阶非线性光学系数。在当时有限的实验设备条件下，面对已知的海量有机和无机化合物，利用“炒菜”式方法来盲目搜索二阶光学效应大的晶体材料，不但效率低，而且极其困难，犹如大海捞针。1964年，Miller提出了经典Miller规则[5]，为钙钛矿型和钨青铜矿型非线性光学材料的发现奠定了理论模型基础。从20世纪60年代中期到80年代初期，随着被研究的非线性光学材料数目的增加，通过大量的实验数据分析积累，研究人员认识到如果能够发展出阐明构效关系的理论模型，将能为实验人员在浩瀚的材料中进行优质非线性光学材料的选型提供有效的方向和启发。从1965年起到1969年，一系列简单的局域化键参数法被提出并运用于阐明结构与性能关系，包括Bloembergen等[6]提出的非简谐谐振子模型、Jeggo等[7]提出的键参数模型、以及Levine等[8-9]提出的键电荷模型等。这些理论模型成功地解释了sp3杂化四配位型(简单σ键型)非线性光学材料二阶效应的构效关系。到20世纪70年代初，科学家们发现二阶非线性光学效应实际上是由具有非局域化价电子轨道的多原子基本结构单元产生的，而不是主要由具有局域化价电子轨道的双原子单元(简单σ键型)所产生。据此，Davydov等[10]于1970年提出了具有施主-受主极性官能团的共轭有机分子的电荷转移模型，有利地推动了非线性光学材料，特别是有机非线性光学材料的发展。

1968年Kurtz等[11]提出了粉末倍频测试方法，可以不需要生长出单晶，只需要实验合成出粉末样品就能够快速地评估非线性光学材料的二阶倍频效应量级以及是否可以实现相位匹配。1981年Tang等[12]对粉末倍频方法作了改进，使之可以进一步获得材料的相位匹配范围。这些实验方法的发展，不仅能够高效准确地确定晶体材料的非线性光学效应量级，极大地加快非线性光学材料关键性能参数的获得和表征，而且能够有效地验证不同的理论模型方法计算和预测的正确性及有效性。理论模型和实验技术的不断发展和相互促进，大大提高了20世纪80年代以来新型紫外非线性光学材料的发展速度。

20世纪60年代末，陈创天研究组对钙钛矿型、钨青铜矿型、BaTiO3和LiNbO3等非线性光学材料的结构与倍频效应进行了深入研究，于1976年~1979年间陆续发表了系列文章[13-16]，提出了阴离子基团理论。这一理论的提出，为非线性光学材料特别是硼酸盐紫外非线性光学晶体探索提供了坚实的理论支持。结合实验工作，我国科学家率先在硼酸盐体系中开展了系统的新型非线性光学晶体探索研究，从20世纪80年代开始陆续发现了一批具有优秀性能的硼酸盐紫外非线性光学晶体，例如被誉为“中国牌”晶体的β-BaB2O4(BBO)和LiB3O5(LBO)等[3]。随后，在20世纪90年代陈创天研究组又发现了能输出迄今为止最短倍频波长的深紫外硼酸盐晶体KBe2BO3F2(KBBF)[18]。这些新型硼酸盐非线性光学晶体的发现和开发，极大地促进了紫外和深紫外全固态激光光源的发展，为激光相关科技领域的进步奠定了物质基础。

20世纪90年代末，陈创天研究组在阴离子基团理论的基础上，结合先进的分析手段以及实验探索方法，在分子设计的层面上进行材料研究，建立了适用于非线性光学晶体材料探索的分子设计专家系统[17]，对性能优秀、具有应用前景的紫外非线性光学晶体进行了系统研究，并总结了其应满足的性能指标。随着近年来计算机硬件和材料计算模拟软件的迅猛发展，第一性原理计算模拟及构效分析已成为新材料探索的一个重要手段。专业研究人员可以无任何经验参数地直接预测出材料性质，并定量分析获得结构与性能之间的本质联系[3]。这进一步完善了非线性光学晶体分子设计体系，并为提高非线性光学晶体的探索效率带来可能性。

从非线性光学材料探索的发展历程来看，基于分子工程学方法的理论模拟和实验合成紧密结合，是一条先进的、行之有效的探索新型、优质紫外非线性光学晶体的研究途径，也是大势所趋。在下面的章节中，将阐述阴离子基团理论和第一性原理方法及其在紫外非线性光学晶体探索中的应用；讨论在深入研究构效关系的基础上，如何建立以分子工程学为基础的专家系统；在紫外非线性光学晶体探索中进行分子设计；展望了非线性光学晶体探索的发展方向。

2阴离子基团理论

阴离子基团理论主要基于以下两点假设[19]：①晶体的宏观倍频系数是由阴离子基团的微观二阶极化张量的几何叠加，而与球形对称的A位阳离子无关；②阴离子基团的微观二阶极化率由对基团局域化轨道波函数的二级微扰获得,晶体的宏观倍频系数计算公式为：

阴离子理论模型的发展，对无机非线性光学晶体特别是紫外倍频材料的探索，提供了极为重要的结构选型支持。例如，在紫外硼酸盐非线性光学晶体中，通过大量的理论模拟工作，发现并证实了决定其倍频效应大小的基本因素(材料倍频基因)就是材料中阴离子基团——硼氧基团的构型和分布取向。表1列出了使用CNDO和Gaussian’92量子化学计算程序包得到的几种典型的硼氧基本结构单元的微观二阶极化率[20]。从表1中可以看出，在硼氧基团中具有共轭π轨道电子结构的(B3O6)3-阴离子基团具有很大的微观二阶极化率，(B3O7)5-和(BO3)3-基团次之，而具有四面体结构的(BO4)5-基团,由于各向异性不明显，其微观二阶极化率最小。

表1　硼氧基团的微观二阶极化率/10-31esu[20]

图1画出了两种具有代表性的硼酸盐非线性光学晶体BBO和LBO结构图。BBO晶体中的阴离子基团是(B3O6)3-基团，它们层状排列，而A位阳离子Ba2+位于层间；LBO晶体中的阴离子基团是(B3O7)5-基团，它们相互连接呈现螺旋结构，而A位阳离子Li+位于空隙中。表2列出了利用阴离子基团理论方法，通过阴离子基团微观二阶极化率的几何叠加，得到的BBO和LBO晶体的倍频系数，并与实验测量值进行了比较[20]。显然，理论计算值与实验值符合得很好，这充分证明了阴离子基团理论在紫外非线性光学晶体倍频效应预测中的合理性和有效性。这一理论模型阐明了此类材料非线性光学效应的内在构效关系。

图1　BBO (a)和 LBO (b)的晶体结构图。图中虚线圆圈分别标出了(B3O6)3-基团和(B3O7)5-基团。B、O、Ba和Li分别由、、和 表示Fig.1　Unit cell of BBO (a) and LBO (b). [B3O6]3- group and [B3O7]5- group are indicated by the dashed circles. B, O, Ba and Li ions are represented by ,, and balls, respectively

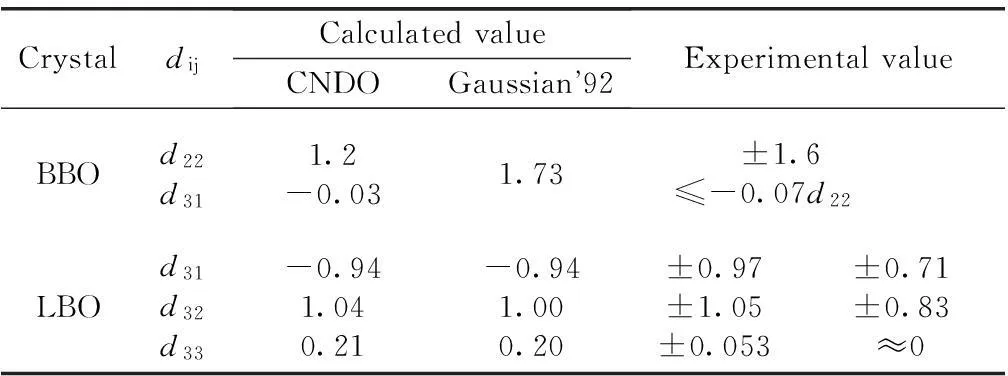
CrystaldijCalculatedvalueCNDOGaussian92ExperimentalvalueBBOd22d311.2-0.031.73 ±1.6 ≤-0.07d22LBOd31d32d33-0.941.040.21-0.941.000.20±0.97±1.05±0.053±0.71±0.83≈0

3第一性原理计算模拟

近年来密度泛函理论(DFT)[21]在研究材料物性方面取得了巨大的成功。伴随着超级计算硬件呈现的几何量级式的更新和发展，人们能够对具有复杂结构的晶体材料物化性质进行高精度的第一性原理计算、模拟和分析。目前常用DFT方法中的局域密度近似(LDA)[22]和广义梯度近似(GGA)[23]，虽然因为交换相关密度泛函的不连续性，在表征材料的激发态时还存在着问题，但是由于主要关心的双折射率和倍频效应本质是对材料基态波函数的微扰，因此这些光学性质在现有的DFT方法框架下可以得到很好的描述。另外，随着DFT交换相关函数的发展，紫外非线性光学材料的带隙预测问题正在逐步得到解决[24-26]。

作者团队在前人工作的基础上，使用基于密度泛函理论的平面波赝势方法[27]，通过计算非线性光学晶体的电子结构，考虑其在外界光场作用下的虚激发过程，计算模拟获得晶体的折射率、双折射率和倍频系数等关键光学性能参数[26]。同时，还发展了“实空间原子切割技术”[28]和“倍频电荷密度权重分析”[29]等一系列探索材料构效关系的分析工具，可以定量和直观地评估紫外非线性光学晶体中各个离子基团对于倍频效应的贡献，从而使得第一性原理方法适用于阐明非线性光学晶体结构与性能的内在联系。

表3列出了第一性原理方法计算得到的BBO和LBO晶体的带隙、折射率、双折射率以及倍频系数。这些理论结果与实验测量符合得很好，证明了第一性原理计算的可靠性和精确性[28, 30]。表4给出了BBO和LBO晶体中利用“实空间原子切割技术”得到的各个离子基团对于折射率、双折射率以及倍频系数的贡献[28, 30]。显然，虽然A位阳离子Li+或Ba2+对于折射率有一定的贡献，但是它们对于双折射率的贡献非常小，可以忽略不计。也就是说，双折射率是由硼氧基团所决定的。更重要的是，随着离子半径的增大，虽然A位阳离子(Ba2+)对倍频效应具有一定的贡献，但其贡献小于20%，即硼氧基团的贡献占80%以上。这充分证明了阴离子基团理论在紫外硼酸盐晶体中的正确性。

表3　第一性原理计算得到的BBO和LBO光学性质与实验值的比较[28, 30]

表4　BBO和LBO晶体中各个离子基团对于光学性质的贡献[28, 30]

以上结论也可以由“倍频电荷密度权重分析”直观地获得(见图2)[26，29]。虽然A位阳离子周围有很大的电子云分布，但是对微观二阶极化率有贡献的电子轨道都集中在硼氧基团上，其决定了晶体宏观倍频效应的大小。

图2　BBO晶体中总体电子分布图(a)；对倍频效应有贡献的电子云分布图(b)[26,29]Fig.2　Charge density (a) and SHG density (b) on the plane of the (B3O6) group in BBO[26,29]

基于第一性原理的材料模拟，不仅能够无经验参数地获得紫外非线性光学晶体中各个离子基团对于倍频效应的贡献，而且能够对于其它关键光学性能参数如晶体带隙、折射率、双折射率等进行准确的计算和预测[26]。阴离子基团理论和第一性原理模拟方法的有机结合，能够更加准确地评估非线性光学晶体的性能并阐明其结构与性能关系，从而为搜索和设计性能优秀的紫外非线性光学材料提供行之有效的理论支持。

4分子工程学方法探索

分子工程学是针对某种特定功能需求，在分子水平上实现结构设计和施工的新思路和新方法。在阐明微观结构起源的基础上，首先在光学功能材料体系中根据其功能需求设计原子结构，然后选择或创制基元，构筑结构，最后采用恰当的方式组装基元实现预定功能。这些研究内容的有机联系，皆以揭示和发展功能、结构和合成3个重要环节之间本质关联为基础。分子工程学在研究方法上从对象到内容皆与传统方法不同：①在研究对象上，它以功能为导向，在分子水平上进行结构设计，研究对象不再局限于单个化合物，而是着重在功能体系上。这一功能体系的结构比传统研究方法的结构更广泛，不仅指分子结构，还包括所有具有特定功能的结构层次，如电子结构、晶体缺陷及凝聚态多层次复合结构等；②在研究内容上，它更加重视了解功能的物理与化学基础，尤其是贯通功能、结构及合成3者之间关系的原理，从材料微观尺度上进行“量体裁衣”式的改进和调控。分子工程的3个环节通过不断反复，以实现基元的有效组合，构建理想结构，达到最佳功能。

从紫外和深紫外非线性光学应用的角度来看，以(B3O6)3-基团和(B3O7)5-基团为骨架的硼酸盐晶体还具有一定的结构局限性。(B3O6)3-基团在晶体结构中往往是孤立存在的，这造成终端氧离子上非成键电子轨道(悬挂键)的聚集，从而引起晶体的紫外截止边红移(带隙变小)，如BBO的紫外截止边仅为189 nm(带隙6.56 eV)[19]；而(B3O7)5-基团在空间相互连接形成的螺旋状网络结构，其双折射率较小，如LBO晶体的双折射率Δn< 0.05[19]。因此，为探索其它具有优秀光学性能的紫外非线性光学晶体，我国科学家通过大量的实验数据和计算模拟积累认识到，当(BO3)3-基团在晶体结构中满足平行同向的排布规律并且终端氧上没有非键轨道时，可以获得较为理想的紫外和深紫外非线性光学性能[19]。

自20世纪90年代以来，我国研究人员陆续发现了一系列具有优秀紫外光学性能的硼酸盐非线性光学晶体，如Sr2Be2B2O7[31]、KBBF[32]、K2Al2B2O7[33]、BaAl2B2O7[34]等。其中KBBF晶体的深紫外谐波转换性能最为优秀，其单胞结构如图3所示。KBBF的原子结构由相互平行并垂直于c轴的二维无限(Be2F2BO3)n→∞层和位于层间的K+离子组成。所有的(BO3)3-基团取向完全一致，而且所有的终端氧都与邻近的铍离子相连。这样的原子排布方式，导致KBBF不仅具有较大的双折射率(Δn~ 0.088 @ 532 nm)和倍频系数(d11=0.49 pm/V)，而且还具有非常大的带隙(8.30 eV)和紫外截止边(155 nm)[18]。KBBF晶体是目前唯一具有深紫外直接倍频能力的深紫外非线性光学晶体，利用棱镜耦合技术，获得了瓦级193 nm平均功率输出和超过30 mW的177.3 nm平均功率输出[18]，并在超高分辨率

图3　KBBF晶体结构:单胞结构(a)和(Be2F2BO3)n→∞层(b)[32]Fig.3　Structure of KBBF：unit cell(a) and (Be2F2BO3)n→∞layer (b) [32]

光电子能谱仪上得到了应用，为我国先进仪器设备的研制提供了关键核心材料，在全固态激光器应用中取得了重大突破。

我国研究人员在阴离子基团理论、第一性原理模拟以及丰富的实验数据积累相结合的基础上，通过数十年的艰辛努力，逐步建立和完善了一套以理论计算、结构搜索、化学合成、粉末倍频效应测试、单晶生长等实验和理论紧密相扣的、先进的非线性光学晶体探索分子工程学专家系统，其研究线路图如图4所示。首先从经验或半经验的模型(如阴离子基团理论)出发，在无机晶体结构数据库(Inorganic Crystal Structural Database, ICSD)中搜寻甚至设计新型化合物，然后通过第一性原理计算获得其关键光学参数(包括带隙、折射率、双折射率、倍频系数等)，确定符合紫外光学性能要求的候选化合物或结构类型，同时也可使用计算模拟进行候选化合物的结构稳定性、热学性质等物化性能评估，与实验快速合成和快速测量得到的结果相互印证。如果计算结果与实验结果不相符，将重新回到理论模型和计算模拟中，进行理论方法的改进以及结构与性能内在联系的再认识。对于两者相符的候选化合物，在充分确定材料构效关系的基础上，进行新型非线性光学材料的搜索和分子设计，对于具有优良性能的材料再进一步进行目标化合物的单晶生长和更精确的测试，确定其实用前景。

图4　紫外非线性光学晶体分子设计专家系统路线图Fig.4　Flow chart for the molecular design system of ultraviolet nonlinear optical crystals

5结语

先进全固态激光技术的发展对非线性光学晶体的性能，例如工作波段、转换效率、抗激光损伤阈值以及晶体生长特性等都提出了更高的要求。近10年来，随着国际上计算模拟软件和硬件的发展，在材料科学领域多学科交叉融合探索新材料的趋势影响下，我国对新材料的计算模拟探索和设计能力也在逐步提高，分析手段也越来越多元化，不少新的理论研究思路和技术手段已经开始应用在非线性光学晶体的理论模拟工作中。其中密度泛函理论等先进的第一性计算模拟手段在新材料探索的研究工作中起到了非常重要的作用，不仅可以较准确地预测材料的光学性质和物化性能，而且也可以与实验相结合获得详细的生长相图。另外，从头计算方法也可用于验证和改进半经验的阴离子基团理论模型，使之能够进一步推广到中远红外非线性光学材料的结构选型中。

中远红外相干光源在激光制导、红外干扰、通信、遥感、微量气体探测等军用和民用领域都有广泛的应用。但是，中远红外非线性光学晶体研究目前还处在国外主导阶段，已有的AgGaS2[35]、AgGaSe2[36]、ZnGeP2[37]等传统红外晶体因激光损伤阈值较低或双光子吸收等问题，限制了其在中高功率激光方面的应用。同时，由于激光核聚变及下一代聚变核能研究的需求，亟需开展特大尺寸的高质量非线性光学晶体生长特性的研究。因此，探索和开发综合性能(包括非线性光学性能、晶体物化性能、生长特性、加工性能等)更为优秀的新型晶体材料刻不容缓。

一种优质的非线性光学材料从发现到最后实用化，仍然需要10~20 a左右的时间。因此迫切需要研究人员在非线性光学材料探索时：①加强多学科协作，在分子工程学研究的基础上，利用高通量理论模拟平台，使用第一性原理计算工具，大规模从头计算材料的光学参数、物化性能、生长相图等，发展先进的高通量实验方法，进行大批次的材料合成和关键性能测定等;②在海量模拟和实验数据的基础上，建立全面详实的非线性光学材料“基因”数据库，通过数据的比较、分析和挖掘，阐明微观结构特征与宏观光学性能的本质联系，获得优质非线性光学材料的选型标准，进行结构设计优化，做到有的放矢;③建立起一套快速、低耗、创新型的非线性光学材料预测、设计、搜索和优化的研发系统。

参考文献References

[1]Cyranoski D. Materials Science: China’s Crystal Cache [J].Nature, 2009,457(7 232): 953-955.

[2]Jones-Bey H. Deep-UV Applications Await Improved Nonlinear Optics [J].LaserFocusWorld, 1998,34(8):127.

[3]Chen C T, Sasaki K, Li R K,etal.NonlinearOpticalBorateCrystals，PrinciplesandApplications[M].Weinheim-Germany: Wiley-VCH, 2012.

[4]Franken P A, Weinreich G, Peters C W,etal. Generation of Optical Harmonics [J].PhysicalReviewLetters,1961,7(4): 118-119.

[5]Miller R C. Optical Second Harmonic Generation in Piezoelectric Crystals[J].AppliedPhysicsLetters, 1964,5(1): 17-19.

[6]Bloembergen N.NonlinearOptics[M]. New York: Benjamin, 1965: 5-8.

[7]Jeggo C R, Boyd G D. Nonlinear Optical Polarizability of Niobium-Oxygen Bond [J].JournalofAppliedPhysics, 1970,41(6): 2 741-2 743.

[8]Levine B F. Electrodynamical Bond-Charge Calculation of Nonlinear Optical Susceptibilities [J].PhysicalReviewLetters, 1969,22(15): 787-789.

[9]Levine B F. A New Contribution to Nonlinear Optical Susceptibility Arising from Unequal Atomic Radii [J].PhysicalReviewLetters, 1970,25(7): 440-442.

[10]Davydov B L, Derkache L D, Dunina V V,etal. Connection Between Charge Transfer and Laser Second Harmonic Generation [J].JETPLetters, 1970,12(1): 24.

[11]Kurtz S K, Perry T T. A Powder Technique for Evaluation of Nonlinear Optical Materials [J].JournalofAppliedPhysics, 1968,39(8): 3 798-3 813.

[12]Halbout J M, Blit S, Tang C L.Evaluation of the Phase-Matching Properties of Nonlinear Optical Materials in the Powder Form [J].IEEEJournalofQuantumElectronics, 1981,17: 513.

[13]Chen Chuangtian(陈创天). 晶体电光和非线性光学效应的离子基团理论(Ⅰ)-利用氧八面体畸变模型计算BaTiO3晶体电光及倍频系数 [J].ActaPhysicaSinica(物理学报), 1976, 25(2): 56-71.

[14]Chen Chuangtian(陈创天). 晶体电光和非线性光学效应的离子基团理论(Ⅱ)-利用(IO3)1-离子基团的分子轨道计算α-LiIO3晶体的倍频系数 [J].ActaPhysicaSinica(物理学报), 1977, 26(2): 32-40.

[15]Chen Chuangtian(陈创天). 晶体电光和非线性光学效应的离子基团理论(Ⅲ)-利用畸变氧八面体的离子基团模型计算LiNbO3, LiTaO3, KNbO3, BNN晶体的电光和倍频系数 [J].ActaPhysicaSinica(物理学报), 1977, 26(6): 28-41.

[16]Chen Chuangtian(陈创天). 晶体电光和非线性光学效应的离子基团理论(IV)-钙钛矿、钨青铜型、LiNbO3型晶体线性极化率计算 [J].JournalofSyntheticCrystals,1978, 27(1): 41-45.

[17]Chen C T, Ye N, Lin J,etal. Computer-Assisted Search for Nonlinear Optical Crystals [J].AdvancedMaterials, 1999,11(13): 1 071-1 078.

[18]Chen C T, Wang G L, Wang X Y,etal. Deep-UV Nonlinear Optical Crystal KBe2BO3F2——Discovery, Growth, Optical Properties and Applications [J].AppliedPhysicsB-LasersandOptics, 2009,97(1): 9-25.

[19]Chen C T, Lin Z, Wang Z. The Development of New Borate-Based UV Nonlinear Optical Crystals [J].AppliedPhysicsB-LasersandOptics, 2005,80(1): 1-25.

[20]Lin Z S, Lin J, Wang Z Z,etal. Theoretical Calculations and Predictions of the Nonlinear Optical Coefficients of Borate Crystals [J].JournalofPhysics-CondensedMatter, 2001,13(23): R369-R384.

[21]Kohn W. Nobel Lecture: Electronic Structure of Matter——Wave Functions and Density Functionals [J].ReviewsofModernPhysics, 1999,71(5):1 253-1 266.

[22]Ceperley D M, Alder B J. Ground-State of the Electron-Gas by a Stochastic Method [J].PhysicalReviewLetters, 1980,45(7): 566-569.

[23]Perdew J P, Burke K, Ernzerhof M. Generalized Gradient Approximation Made Simple [J].PhysicalReviewLetters, 1996,77(10): 3 865-3 868.

[24]Lin Z S, Kang L, Zheng T,etal. Strategy for the Optical Property Studies in Ultraviolet Nonlinear Optical Crystals from Density Functional Theory [J].ComputationalMaterialsScience, 2012,60: 99-104.

[25]He R, Huang H W, Kang L,etal. Bandgaps in the Deep Ultraviolet Borate Crystals: Prediction and Improvement [J].AppliedPhysicsLetters, 2013,102(23): 231 904.

[26]Lin Z S, Jiang X X, Kang L,etal. First-Principles Materials Applications and Design of Nonlinear Optical Crystals [J].JournalofPhysicsD-AppliedPhysics, 2014,47(25):253 001.

[27]Payne M C, Teter M P, Allan D C,etal. Iterative Minimization Techniques for Ab Initio Total-Energy Calculations-Molecular-Dynamics and Conjugate Gradients [J].ReviewsofModernPhysics, 1992,64(4): 1 045-1 097.

[28]Lin J, Lee M H, Liu Z P,etal. Mechanism for Linear and Nonlinear Optical Effects in beta-BaB2O4Crystals [J].PhysicalReviewB, 1999,60(19): 13 380-13 389.

[29]He R, Lin Z S, Lee M H,etal. Ab Initio Studies on the Mechanism for Linear and Nonlinear Optical Effects in YAl3(BO3)4[J].JournalofAppliedPhysics, 2011,109(10):103 510.

[30]Lin Z S, Lin J, Wang Z Z,etal. Mechanism for Linear and Nonlinear Optical Effects in LiB3O5, CsB3O5, and CsLiB6O10Crystals [J].PhysicalReviewB, 2000,62(3): 1 757-1 764.

[31]Chen C T, Wang Y B, Wu B C,etal. Design and Synthesis of an Ultraviolet-Transparent Nonlinear-Optical Crystal Sr2Be2B2O7[J].Nature, 1995,373(6 512): 322-324.

[32]Chen C T, Xu Z Y, Deng D Q,etal. The Vacuum Ultraviolet Phase-Matching Characteristics of Nonlinear Optical KBe2BO3F2Crystal [J].AppliedPhysicsLetters, 1996,68(21): 2 930-2 932.

[33]Ye N, Zeng W R, Jiang J,etal. New Nonlinear Optical Crystal K2Al2B2O7[J].JournaloftheOpticalSocietyofAmericaB-OpticalPhysics, 2000,17(5): 764-768.

[34]Ye N, Zeng W R, Wu B C,etal. Crystal Structure of Barium Aluminium Borate, BaAl2B2O7[J].ZeitschriftFurKristallographie-NewCrystalStructures, 1998,213(3): 452-452.

[35]Boyd G D, Kasper H, Mcfee J H. Linear and Nonlinear Optical Properties of AgGaS2, CuGaS2, andCuInS2, and Theory of Wedge Technique for Measurement of Nonlinear Coefficients [J].IEEEJournalofQuantumElectronics, 1971,7(12): 563.

[36]Tell B, Kasper H M. Optical and Electrical Properties of AgGaS2and AgGaSe2[J].PhysicalReviewB, 1971,4(12): 4 455.

[37]Boyd G D, Buehler E, Storz F G. Linear and Nonlinear Optical Properties of ZnGeP2and CdSe [J].ApplPhysLett, 1971,18: 301-304.

(编辑王方)

特约专栏

Molecular Design for Ultraviolet Nonlinear Optical Crystals

LIN Zheshuai, WU Yicheng

(Key Laboratory of Functional Crystals and Laser Technology，Technical Institute of

Physics and Chemistry, Chinese Academy of Sciences, Beijing 100190, China)

Abstract：Ultraviolet (UV) nonlinear optical (NLO) crystals play crucial role in the applications of the all-solid-state lasers. Exploration on the UV NLO crystals with superior performance is a research hotspot in optoelectronic functional materials, so the key point is how to efficiently find the suitable candidates with optimized structural features. In this work, we review the research history of the structure-property relation in UV NLO crystals, especially focusing on the important roles of anionic group theory and first-principles theory in this topic. These materials calculation methods can not only accurately predict the key optical properties in UV NLO crystals, but also quantitatively and intuitively elucidate the intrinsic relation between property and structure. The strong synergies among materials simulations, target structure searching, compound synthesis, powder NLO test and single crystal growth result in the construction of a molecular design system for the UV NLO crystals. The development of this system may significantly improve the research efficiency and greatly prompt the innovation capability on the NLO crystals in China.

Key words：ultraviolet nonlinear optical crystals; molecular design; structure-property relation; anionic group theory and first-principles method

中图分类号：O561

文献标识码：A

文章编号：1674-3962(2015)04-0257-07

DOI:10.7502/j.issn.1674-3962.2015.04.01

通讯作者:第一作者及林哲帅，男，1974年生，研究员，博士生导师，Email:zslin@mail.ipc.ac.cn

基金项目：国家自然科学基金资助项目(51132008,11174297)

收稿日期：2014-09-26