多元铝合金相图热力学、热物性质数据库及其应用

刘树红，凌缔成，黄丹丹，张　帆，杜　勇

(中南大学 粉末冶金国家重点实验室，湖南 长沙 410083)



特约专栏

多元铝合金相图热力学、热物性质数据库及其应用

刘树红，凌缔成，黄丹丹，张帆，杜勇

(中南大学 粉末冶金国家重点实验室，湖南 长沙 410083)

摘要：精确的热力学、热物性质数据库是对多元多相材料制备过程中微观结构演变定量描述的关键。高性能铝合金作为航空航天和国民生产用重要结构材料，其制备工艺的优化和设计一直备受关注。首先概述了多元多相铝合金热力学数据库构筑的方法及其最新研究进展，重点介绍了多元多相铝合金相平衡的测定方法和TEM、3DAP及第一原理计算在铝合金热力学数据库构筑中的辅助作用。随后介绍了多元多相铝合金扩散系数、粘度、摩尔体积数据库构筑的最新研究进展。给出3个实例介绍了热力学数据库和热物性质数据库在铝合金凝固过程中微观结构演变模拟的应用。最后简单总结了多元铝合金热力学和热物性质数据库目前面临的问题和挑战。

关键词：多元铝合金；相平衡; 热力学数据库；热物性参数；CALPHAD方法

1前言

铝合金具有密度低、耐腐蚀、易塑性加工等特点，广泛应用于航空航天、交通运输、民用建筑等领域。铝合金是仅次于钢铁用量最大的轻质高性能结构材料，其研发水平的高低是衡量国家科技竞争力的核心指标之一。多年来，国内外材料研究者力求通过合金成分和加工工艺的最优化，使铝合金达到所预期的性能。为了更好地指导工程应用，人们力求建立铝合金的性能与成分和加工工艺参数的定量关系。但由于成分和加工工艺参数不是材料性能的状态参量，建立这种定量关系难度极大。微观结构是材料的状态变量和加工历史的指纹，并且决定材料制备过程中的性能变化。揭示与掌握多元多相铝合金制备过程中微观结构演变及其与力学性能的量化关系是材料科学的核心，是实现铝合金性能重大突破的关键。因此，对铝合金制备过程的微观结构演变进行定量描述是设计制备新型铝合金的关键基础研究课题。

近10年来，为了在全球范围内激烈的科学技术竞争中占据主导地位，美、德等西方发达国家及我国相继实施了一系列新材料发展计划[1-4]，旨在显著加快新材料的研发。虽然国际材料界对美国提出的材料基因组计划存在不少争论，但是材料基因组计划所强调的“阐明从原子排列到微观结构的形成规律，通过计算模型与数据库平台以及关键实验相结合对新材料进行成分设计和性能预测，建立材料宏观性能与使用寿命之间的相互关系”观点得到了国际材料界的广泛认可[3]。

精准的热力学、热物性参数输入是对微观结构演变进行定量描述的必备条件。利用热力学数据库和相关热力学计算软件可以获得多组元体系相平衡、亚稳相平衡、仲平衡、各种热力学性质及热力学因子等信息。其中热力学因子也是发展用于微观结构模拟的扩散数据库所需要的重要热力学参数。主要的热物性参数包括扩散系数、界面能、弹性应变能、粘度、热导率、密度等，它们都是温度和成份的函数[5]。

本文将首先对多元多相铝合金热力学数据库构筑的方法做简单介绍，主要介绍多元多相铝合金相平衡的测定方法和TEM、3DAP及第一原理计算在铝合金热力学数据库构筑中的辅助作用。然后介绍多元多相铝合金扩散系数、粘度、摩尔体积等热物性质数据库构筑的最新研究进展。接着将给出3个实例介绍热力学数据库和热物性质数据库在铝合金凝固过程中微观结构演变模拟的应用。最后将探讨多元铝合金热力学和热物性质数据库构筑所面临的挑战。

2多元铝合金热力学数据库的构筑

相图计算领域的学者经过约30年的努力，已经建立了各种多元铝合金热力学数据库。其中最具影响力的商用铝合金热力学数据库有3个：TT-Al[6]、PanAl[7]及TCAL[8]。其中TCAL[6，8]是中南大学相图、相变与材料设计中心与瑞典Thermo-Calc公司合力开发。该数据库目前包含34个元素，445个固溶体和金属间化合物相，是目前国际上包含元素和相最多的多元铝合金热力学数据库。为了获得热力学参数，需要输入相图热力学实验数据。一般来说，高精度的热力学数据库基于合理的热力学模型和精确可靠的相图热力学实验数据。下面将介绍多元多相铝合金相平衡的测定方法和TEM、3DAP及第一原理计算在铝合金热力学数据库构筑中的辅助作用。

2.1多元合金相平衡测定

相图的精确测定需要多种方法综合使用，有关相图实验测定方法的文献和书籍较多[9-11]，在此不再赘述。以三元Al-Ni-Ti[12]体系为例，测定相平衡的一般步骤如下。首先，选择高纯原材料制备合金样品。在Schuster等[12]工作中，高纯Al，Ni，Ti来自德国Karlsruhe的Johnson Matthey Alfa公司，纯度分别为99.99%，99.9+%及99.98%；样品通过电弧熔炼后真空封装于石英管中,而后分别在1 000 ℃、900 ℃、800 ℃ 或600 ℃均匀化退火2周以上并淬火；热处理后的样品经X射线衍射(XRD)分析物相，扫描电镜、能谱分析(SEM/EDX)进行相平衡及成分分析，差示热分析(DTA)获得相变温度；最终获得1 000 ℃、900 ℃、800 ℃ 或600 ℃等温截面及液相面投影图。图1为根据实验数据构筑的Al-Ni-Ti三元系的液相面投影图。

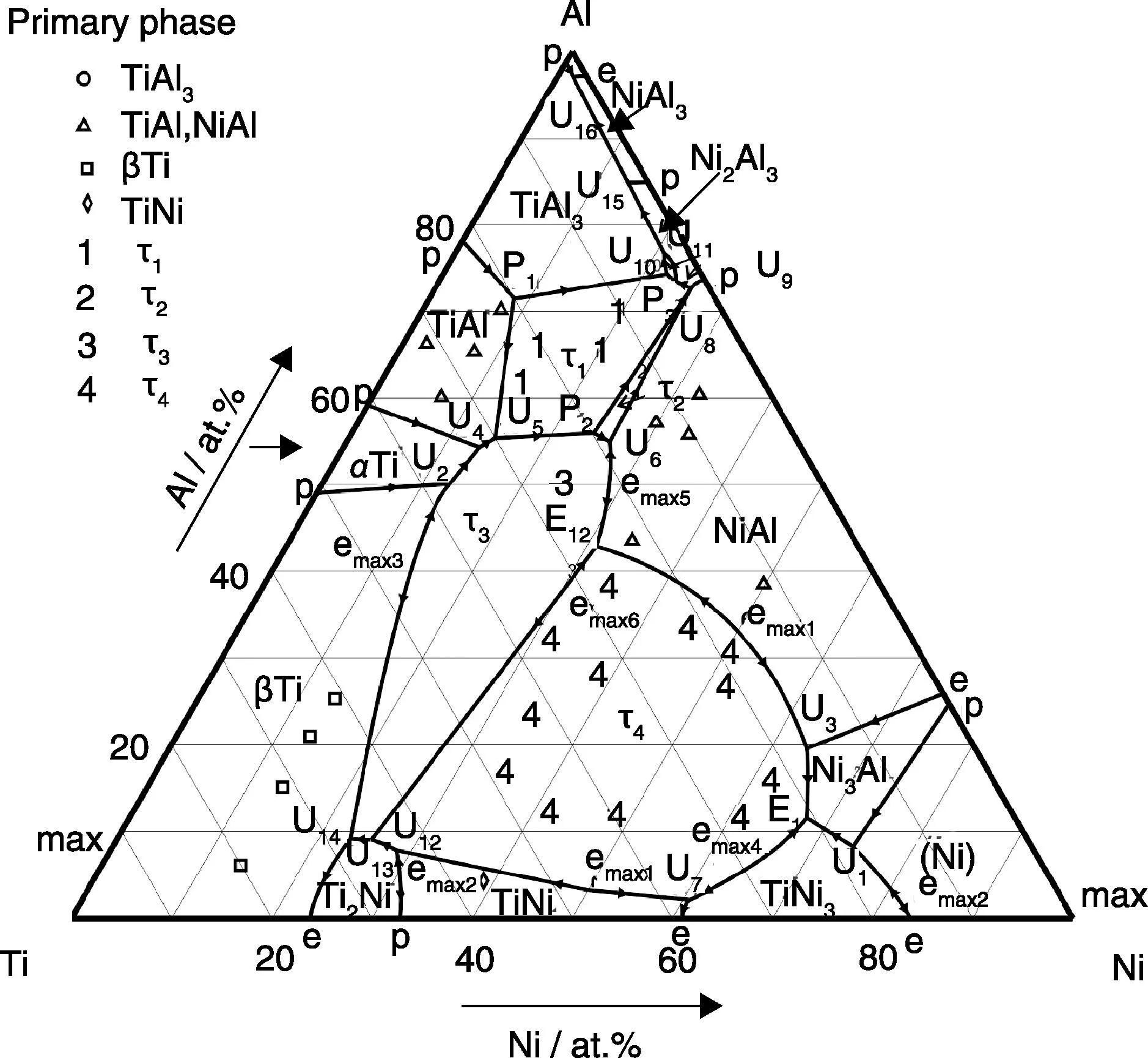
图1　实测的Al-Ni-Ti体系液相面投影图[12] Fig.1　Projection of the liquidus surface in the Al-Ni-Ti system[12]

除了上述介绍的合金法测定相平衡外，扩散偶法结合扫描电镜(SEM)或电子探针(EPMA)也常用来测定合金的相平衡。然而在相平衡测量时常检测到一些纳米尺度相，常规的实验技术(如XRD、EPMA、SEM)在测量这些相的体积分数和成分时往往存在局限。例如：XRD无法检测到微量相的存在，SEM不能分辨尺寸小于10 nm的颗粒，EPMA不能提供尺寸小于1μm的相成分信息。为了准确获得这些纳米尺寸相的相平衡信息，需要具有更高分辨率和灵敏度的分析技术。透射电镜(TEM)和三维原子探针(3DAP)是两种可以满足这种需求的检测技术。本文将举两个例子说明TEM及3DAP结合常规检测方法如何成功获取含纳米尺度相体系的相平衡信息。

2.1.1Al-Fe-Ni-Si体系富铝角相平衡测定

Al-Fe-Ni-Si四元系是铝合金工业重要的合金体系，因为很多商用铝合金均含有Fe，Ni及Si元素。然而关于该体系富铝角相平衡和凝固行为的文献报道非常有限。中南大学的Hao等[13]采用XRD、SEM、EPMA、DTA及TEM分析手段,并与热力学计算的结合，获得了一套描述Al-Fe-Ni-Si体系富铝角相平衡的热力学参数，可以计算该体系富铝角任意温度及成分范围的平衡相图或热力学性质图。

实验发现凝固过程从(Al)基体中析出了许多纳米尺度相。为了表征铸态样品中的纳米尺度相，Hao等[13]采用XRD、SEM结合TEM进行检测分析，最终获得纳米尺度相为(Si)、Al8Fe2Si及 Al9Fe2Si2。图2为铸态89Al-1Fe-2Ni-8Si(原子百分数)合金的TEM照片。沿[-1 1 1]Si晶向的明场相显示许多圆形的纳米尺度相。纳米尺度相的快速傅里叶变换(FFT)花样标定了其晶体结构。这些信息是仅仅采用XRD和SEM无法获得的。

图2　铸态合金89Al-1Fe-2Ni-8Si(原子百分数)的晶体特征：(a) 沿[-111]Si 晶向的TEM明场像，(b)沿[-111]Si晶向的选取衍射花样，(c) Al8Fe2Si相沿[-111]Si晶向的HRTEM照片，(d) Al8Fe2Si相沿<10- 1>快速傅里叶变换花样Fig.2　Crystallographic features of the as-cast 89Al-1Fe-2Ni-8Si(at.%):(a) TEM image viewed along the [-111]Si direction, (b) SAED pattern viewed along the [-111]Si direction, (c) HRTEM image of Al8Fe2Si viewed along the [-111]Si direction and (d) Fast Fourier Transform pattern of Al8Fe2Si along <10-1> in (c)

2.1.2Ni-Al-V体系800 ℃相平衡成分测定

3DAP 可以提供材料中纳米尺度相的三维成分分布图。Ni-Al-V三元体系非常复杂[14]，因为随温度升高，无序结构的γ相与有序结构γ’和θ将在富Ni角共存。而这些相均为纳米尺度颗粒，用EPMA或者SEM/EDX无法测得这些相的成分。Zapolsky等[14]采用3DAP测定了Ni-Al-V体系800 ℃无序γ相及有序γ’和θ相的成分。测定的成分与基于显微平均场法的数值计算结果相吻合。这些实验及计算结果修正了文献中发表的相图[15]。

2.1.3含高挥发性元素铝合金相平衡的实验测定方法

铝合金中常添加高挥发性元素(如Mg，Zn)和高反应活性元素(如Sr，Ca)来改善其性能。常用样品制备方法(如感应熔炼、电弧熔炼)无法精确制备含高挥发、高反应活性元素的铝合金样品。另外，现有差热分析方法，由于是在敞开的坩埚中进行的，不适用于含高挥发、高反应活性元素的铝合金。中南大学的王培生、杜勇等[16]通过系列技术改造，将电子天平、压型机、氩弧焊机置于手套箱中使用，并根据热传导及热分析理论，通过自行改造的可以精确控制的氩弧焊接机，成功制备出了密封性良好的钽坩埚，从而研发出了制备含高挥发性、高反应活性元素的铝合金样品的设备。图3a是采用该设备制备的82Al-12.35Mg-2Sc-3.65Zn(原子百分数)铸态合金的SEM照片，图3b是计算的等温截面与实验数据的比较[17]。可以看出，其研发的设备解决了高挥发性元素对铝合金制备带来的影响，获得了理想的实验结果。

图3　Al-12.35Mg-2Sc-3.65Zn (原子百分数)铸态合金SEM照片(a)，计算的Al-Mg-Sc-Zn体系富Al角的350 ℃等温截面与实验数据的比较(b) Fig.3 　SEM image of as-cast Al-12.35Mg-2Sc-3.65Zn (at.%) (a),the calculated partial isothermal section of Al-Mg-Sc-Zn system with 2 wt.% Sc in the Al rich corner compared with the experimental data (b)

2.2CALPHAD方法与第一原理计算

相图计算方法(CALculation of PHAse Diagrams,CALPHAD)基于热力学基础理论，构建热力学模型来描述材料体系中的各相的热力学性质,并通过拟合由实验、第一原理计算、经验/半经验公式等获得的数据，优化模型参数，进而建立描述材料体系的热力学数据库。1956年，Kaufman和Cohen[18]运用规则溶液模型计算了Fe-Ni相图，标志着相图计算方法的诞生。经过近60年的发展，CALPHAD方法在材料科学和工程界受到越来越多的关注。CALPHAD方法也由最初的相图热力学计算扩展到扩散、粘度、摩尔体积等热物性质研究领域。

近年来，CALPHAD方法与第一原理计算相结合研究材料的热力学性质和热物性质受到越来越多的关注。 基于密度泛函理论的第一原理计算只需输入元素的原子质量和晶体结构信息就可以计算物相的热力学及结构特性。将CALPHAD方法和第一原理计算有效结合，可最大限度地发挥两种计算方法各自的优势，也有助于CALPHAD方法的模型参数基于一定的物理基础。

最近，Wolverton等[19-20]和Liu等[21]的工作证实了第一原理计算预测热力学数据的优势。特别是对于难制备的易氧化、高蒸汽压的合金，其热力学性质很难通过实验直接测量，可以充分利用第一原理计算得到相关数据。此外，对于亚稳相的热力学性质，第一原理计算是唯一有效的计算工具。如果知道声子振动谱，一定温度范围内的热力学性质就可以通过准谐近似方法来获得。Golumbfskie等[22]计算了Al-Ni-Y体系中三元化合物有限温度的热力学性质，计算结果为Al-Ni-Y化合物的热力学模型的构筑提供了重要参考。另外，随着CALPHAD方法的发展，第一原理计算也用于扩散、体积、热膨胀系数、弹性常数、界面结构及界面能等热物性质的计算，从而为相关数据库的建立提供了技术支持。

3多元铝合金热物性质数据库

3.1扩散动力学数据库

多组元铝合金凝固过程中微观结构演变的很多现象都与扩散密切相关[23]。扩散系数分为自扩散系数、杂质扩散系数、示踪扩散系数、互扩散系数和本征扩散系数。扩散理论表明：为描述含n个组元相的扩散行为，需要一个由(n-1)2个扩散系数Dij(i =1…n-1, j=1…n-1)组成的矩阵。为减少描述多元相的扩散所需的参数个数，Anderson等[24]提出了由实测扩散系数获得各元素在相关相中的原子移动性参数，然后再用原子移动性参数计算扩散系数矩阵的方法。根据这一思想，他们开发了DICTRA软件(DIffusion Controlled TRAnsformations)[6]。

目前，发布的商用铝合金扩散动力学数据库有两个MOBAL1和MOBAL3[6]。其中MOBAL1仅包含有限元素fcc和液相的原子移动性参数，而MOBAL3在MOBAL1基础上包含了一些二元体系fcc相的原子移动性参数。

实验数据上的缺陷是建立多组元铝合金原子移动性参数数据库的主要障碍。文献报道的三元或者更多组元体系的扩散数据非常有限，且受实验手段的限制导致不同来源的数据常常不一致。所以亟需一种高效测量整个扩散路径的三元互扩散系数的实验方法。

在二元合金体系中，随成分变化的扩散系数可以通过扩散偶方法结合Boltzmann-Matano方法获得。而在三元合金当中，由于在三元合金的扩散系数矩阵当中，同时存在主扩散系数和交叉扩散系数导致情况会变得复杂。传统的两个扩散偶所构成的交点法工作量巨大，且获得的信息量很少。为了提高测定扩散系数的效率并获得成分相关的三元扩散系数，捷克科学家Cermak和Rothva[25]率先报道了一种采用单一扩散偶计算成分相关扩散系数的方法(称为Cermak-Rothva方法)。Cermak-Rothva方法基于Dayananda通过单一扩散偶计算平均扩散系数的方法，将平均扩散系数的计算局限在无限小的成分范围内来实现随成分变化的扩散系数的计算。中南大学的Cheng和Chen等[26-27]从菲克定律出发，推导了Cermak-Rothva方法的微分形式，从物理意义和数学形式两个角度证实了Cermak-Rothva方法的不足之处，并提出了一种通过一个三元扩散偶测定随成分变化的互扩散系数的实用高效方法，且编写了相应程序。图4为用新提出的方法计算的Co-Fe-Ni三元扩散偶的互扩散系数，所得结果与传统的Matano-Kirkaldy方法所得到的数据相吻合，进一步证明了该方法的可靠性。

液相扩散系数是表征合金凝固过程中微结构演变的重要热物性参数。由于微重力及液相具有对流、活跃的化学反应等特性，对液相扩散系数进行精准的实验测定一直困扰着材料领域的科学家们，这就使得理论计算显得更加重要。最近，中南大学的Chen等[28]通过考虑溶质和溶剂的尺寸效应，对Sutherland公式进行了修正，从而准确预测了各种元素液态自扩散系数和杂质扩散系数。基于修正的Sutherland公式，Chen等[28]建立了二元及多元合金中粘度和扩散系数的关系，并耦合热力学数据库实现了二元及多元合金示踪扩散系数和互扩散系数的精准预测。图5是基于修正的Sutherland公式预测的Al-Cu合金液相的互扩散系数分别与实验值的对比。

图4　采用新型高效方法计算的Co/Co-37 at.%Fe-45 at.%Ni (a)和Co-49 at.%Ni/Co-41 at.%Fe (b)三元扩散偶的成分距离曲线、互扩散通量曲线和相应的互扩散系数，并与实验数据相对比[26-27]Fig.4　Calculated concentration profiles , interdiffusion flux curves and interdiffusivities for the ternary diffusion couples Co/Co-37 at.%Fe-45 at.%Ni(a)and Co-49 at.%Ni/Co-41 at.%Fe (b)using the pragmatic method[26-27]

图5　基于修正的Sutherland公式预测的Al-Cu液相互扩散系数与实验值的对比[28]Fig.5　Calculated inter-diffusivities in liquid Al-18.7 at.% Cu and Al-40 at.% Cu alloys with the modified Sutherland equation, compared with the measured data[28]

此外，获得亚稳相精确的扩散系数是扩散领域亟需解决的一大难题。在过去的几十年中，已经发展了多种计算各种扩散系数的方法，如第一原理计算方法、分子动力学模拟、半经验方法以及DICTRA模拟。最近，许多国内外学者采用第一原理计算进行了相关研究。Mantina等[29]使用第一原理计算方法预测了Mg，Si及Cu在稀薄fcc相铝中的杂质扩散系数。基于单空位扩散机制，采用晶格振动、NEB(Nudged Elastic Method)以及TST(Transitional State Theory)过渡态理论，Xin等[30]采用第一原理计算了Al-Cu-Mg体系fcc相的扩散系数。图6是计算的Mg在fcc Al中的杂质扩散系数同实验数据的比较，计算结果与实验数据吻合较好。这一工作可望为构筑多元铝合金扩散动力学数据库提供重要数据。

图6　第一原理计算的Mg在fcc Al中的杂质扩散系数同实验数据的比较 [30]Fig.6　Calculated impurity-diffusion coefficient of Mg in fcc Al[30], compared with the experimental work

3.2摩尔体积数据库

体积的变化伴随在凝固及后续热处理过程中。摩尔体积是进行准确微观结构演变模拟必须考虑的热物性质之一。尽管体积对吉布斯自由能的贡献在常温常压下可忽略不计，但是当压力作为变量计入研究范围，其影响便无法忽视。因而，有必要建立模型描述摩尔体积并构筑摩尔体积数据库。尽管近几年来，有很多关于摩尔体积模型和实验的研究，但目前还没有系统报道的商用CALPHAD-类型摩尔体积数据库。纯组元摩尔体积的完整表达是构筑摩尔体积数据库的关键。根据吉布斯自由能状态方程，摩尔体积应包含两部分：与温度相关的部分和与压力相关的部分。下面将首先介绍目前常用的几种描述纯组元摩尔体积的计算模型。

3.2.1基于线性热膨胀系数和Grover经验式的模型

考虑吉布斯自由能的贡献，基于改进的Grover 经验式[31]，Lu等[32]推导出如式(1)关系来描述非磁性材料的摩尔体积与压强的关系：

(1)

V(T,P0)=V0exp(VA)

(2)

其中V0为参考温度 T0时的摩尔体积，VA为体积膨胀系数3α的积分，a, b, c, d分别为与温度有关的参数，其值可从常压下大量实验数据评估而得。

对于磁性材料, 磁性对摩尔体积的贡献可以表示为式(3)，

(3)

Fernandez Guillermet[34]用该磁性模型成功描述了磁性对hcp Co和 fcc Co摩尔体积的贡献。图7是Lu 等[32]根据以上模型计算的压强低于100 GPa时Fe的T-P相图，计算结果能够合理地描述实验数据。

图7　优化计算的Fe的T-P相图[32](图中符号为实验值)Fig.7　Calculated T-P phase diagram of pure Fe[32], compared with the experimental data

3.2.2基于Debye-Grüneisen 模型的CALPHAD Helmholtz能量模型

公式(1)所述模型往往在超出一定温度和压力时会出现负熵和负热容等异常现象[35]。对此Lu等[36-37]基于Debye-Grüneisen 模型提出了CALPHAD Helmholtz能量模型，成功描述了常压及高压下fcc Cu的热力学性质及热物性质。

对于非磁性材料体系, 总的Helmholtz 能量F主要由绝对0 K下静态晶格能Etot、晶格振动能FD和电子热激发能Fel3部分组成：

F(T,V)=Etot(V)+FD(T,V)+Fel(T,V)

=Etot(V)+ED(T,V)-TSD(T,V)

+Eel(T,V)-TSel(T,V)

(4)

其中T是温度，V是体积，ED和SD分别为晶格振动能和振动熵，Eel和Sel分别对应于电子热激发产生的能量和熵。由于压强是Helmholtz能对体积的负偏导，在一定的温度和压强下，研究体系的平衡体积和能量可以通过求Helmholtz能偏导确定。图8为基于Lu和Chen[37]获得的模型参数计算的fcc Cu在高压和室温的摩尔体积，可以合理地描述实验数据。

图8　Lu和Chen[37]计算的fcc Cu 在298 K和高压下的摩尔体积与实验数据的比较Fig.8　Comparison between calculated molar volume of fcc Cu at 298 K and high pressures[37] and experimental data

3.2.3 基于SGTE和准谐模型的CALPHAD相容性模型

针对传统模型可能出现的反常物理现象，Brosh等[38]提出另一种表达式，将SGTE数据库与准谐模型相结合用于描述常压与高压下的吉布斯自由能，从而可同时描述所研究体系的热力学和热物性质。Brosh等[38]提出的模型吉布斯自由能表达如式(5)：

G(T,P)=GC(P)+GQH(T,P)

-[GQH(T,P0)-G(T,P0)]I(P)

(5)

Brosh和Karbasi等[38-39]分别利用上述模型对部分金属纯元素、氧化物的热容、体积和弹性模量等热力学及热物性质进行了系统研究。同文献报道的其他方法相比，他们的模型可以用更少的参数合理地描述实验数据。

对于二元体系，一般采用 Redlich-Kister 多项式表达：

(6)

其中 Vi为纯组元i的摩尔体积, xi为纯组元i的摩尔分数,VE为超额摩尔体积。

Hallstedt[40]根据二元实验数据的线性外推对室温常压状态下的亚稳相的摩尔体积进行估测，并构筑了部分二元体系在298 K及105Pa压强下摩尔体积随成分的变化关系。作者研究小组最近也做了一些相关工作，系统研究了Al-Cu-Mg-Si体系fcc、bcc、hcp相的摩尔体积，图9是采用作者小组所得的参数计算的不同Cu含量的Al-Cu合金密度随温度变化曲线与实验值的比较。计算结果能够合理地描述实验数据。

图9　计算的不同Cu含量Al-Cu合金密度随温度变化曲线，及与实验值的比较 Fig.9　Calculated density of Al-Cu alloys with the different content of Cu versus temperature, compared with experimental data

3.3粘度

粘滞性是液态金属的重要热物性质之一，是研究液态金属特性的重要途径。粘度是度量粘滞性的物理量，它决定着液态金属的流体力学特性，同时也影响着流体的传热和传质特性。目前测定液体合金粘度的方法主要有毛细管法和振动法等。然而实验测定粘度是非常繁杂和昂贵的工作，因此很多研究者试图结合热力学参数预测合金体系的粘度性质。但由于准确地描述液体的结构特征[41-42]非常困难，所以他们的工作不能适用于所有的合金体系中。例如Schick等[43]在研究Al-Cu体系粘度性质时发现，现有模型不能合理描述和预测Al-Cu合金粘度随成分变化的规律。他们认为在Al-Cu合金中存在缔合结构，而目前大部分模型没有关注这一点。因此，他们提出了一种新的方法进行描述，如式(7)所示：

(7)

(8)

(9)

然而作者所在研究小组将其应用到Al-Mg体系中时，预测结果与实验数据仍然存在一定差距。因此提出一种更加准确的描述不同温度不同成分的模型是非常必要的。

一般情况下，纯元素的粘度随温度的变化规律符合Arrhenius方程，如式(10)所示：

(10)

其中η0为前置因子，E为激活能。

对于二元体系，CALPHAD类型的模型能合理描述粘度随温度和成分变化，如式(11)所示：

η=cAηA+cBηB+cAcBηE

(11)

它包含两部分，一部分为理想混合部分(cAηA+cBηB)，另一部分为超额部分(cAcBηE)。

对于多元体系，粘度数据可以根据二元体系中的参数外推获得，如式(12)所示：

(12)

采用以上思路可以建立多组元合金体系的粘度数据库。图10为作者研究小组采用CALPHAD类型模型计算的Al-Si二元系粘度与实验数据[44-45]的比较，表明CALPHAD类型的模型是一种非常有效的能合理描述合金体系粘度的方法。

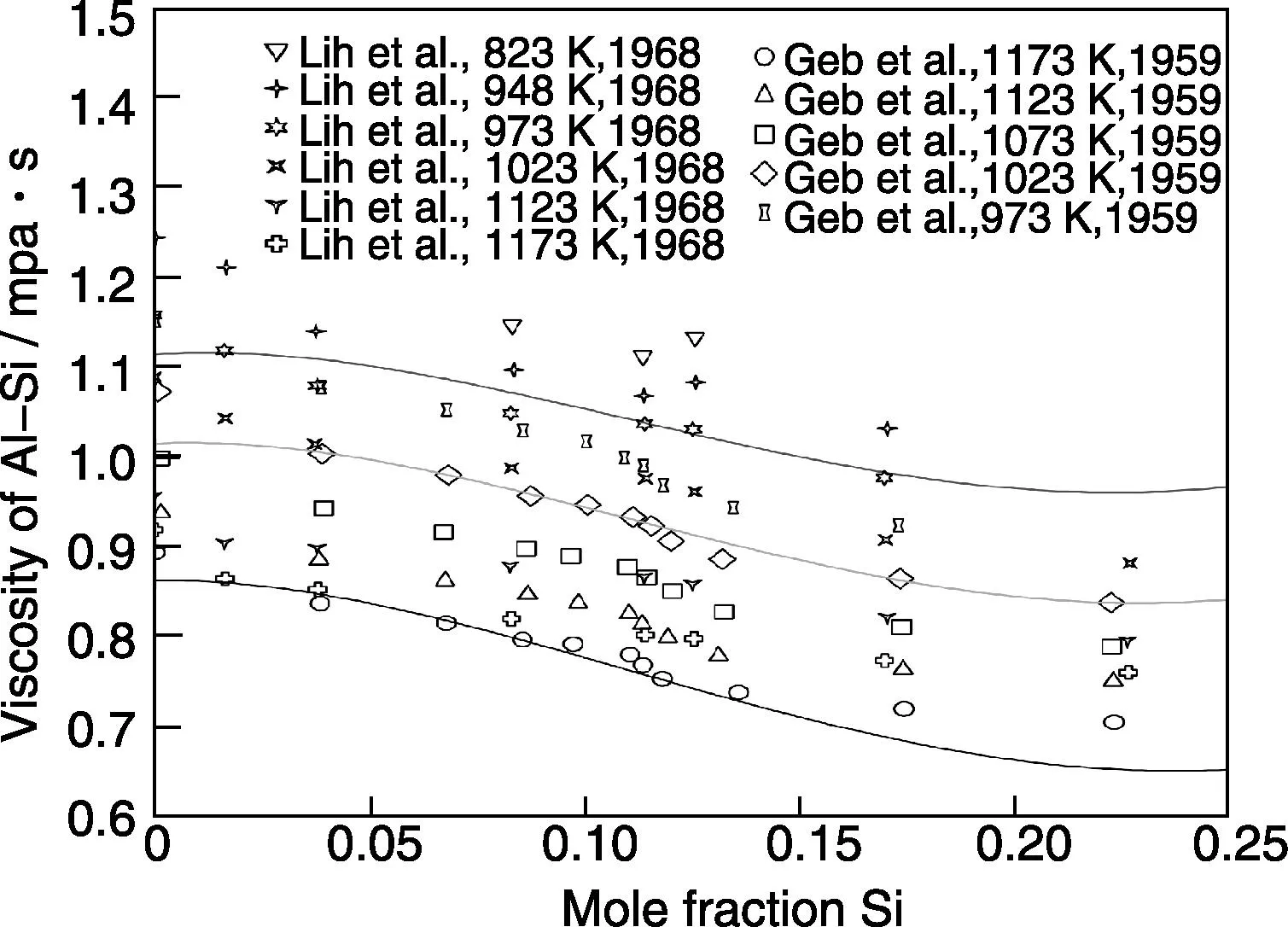
图10　计算的Al-Si体系的粘度与实验结果[44-45]的比较Fig.10　Calculated viscosity of the Al-Si system at different temperatures，compared with the experimental data[44-45]

4 数据库在多元铝合金中的应用

4.1基于热力学数据库研究添加元素对合金凝固行为的影响

由于热膨胀系数低、耐磨性好及硬度高，过共晶Al-Si基合金(如A390)广泛在汽车、航空领域用作连接杆、气缸套、发动机组等。过共晶Al-Si基合金的优良性能来源于其微观结构：细晶粒的初晶Si弥散分布在Al+Si共晶组织中。但在传统铸造过程中由于潜热高及凝固时间长往往导致析出Si粒度粗大，严重影响了合金的机械性能。研究发现Mg2Si可望改善A390合金的机械性能[46]，但其作用机理有待进一步研究。为了设计新一代耐磨铝合金，Hekmat-Ardakan和Ajersch[47]基于热力学计算研究了添加Mg元素对Al-Si A390合金凝固行为的影响。图11为计算的Mg成分对Al-17%Si-4.5%Cu合金相转变及转变温度的影响。结果显示：液相线,二元、三元共晶反应的温度会随着Mg含量的增加而改变； 当Mg含量增加至4.2%时(质量分数)，开始有Mg2Si析出；当Mg含量增加至7.2%时，Mg2Si将取代Si作为初晶相析出。图12为基于Scheil凝固模拟的不同Mg含量的合金凝固过程液相分数随温度的变化。可以明显看出：随着Mg含量达到6%，合金的共晶温度(对应拐点)明显地从566.2 ℃降低到549.7 ℃，而Mg含量从6%增加到10%时，共晶温度变化不大。研究结果对改善Si粒度从而改善A390合金的机械性能具有重要指导意义。

图11　计算的Mg含量对Al-17% Si-4.5% Cu合金相转变及转变温度的影响[47]Fig.11　The effect of Mg content on the phase transitions and the transition temperatures for Al-17% Si-4.5% Cu alloys[47]

图12　基于Scheil凝固模拟的不同Mg含量的合金凝固过程液相分数随温度的变化[47]Fig.12　Comparison of the liquid fraction vs temperature curves for basic A390, 6% Mg and 10% Mg contained alloys during the solidification interval according to Scheil solidification[47]

4.2热力学数据库与热物性质数据库相结合预测合金凝固过程显微组织及显微偏析

A356系合金因其优良的铸造性能被广泛应用于汽车工业。显微组织和显微偏析的准确预测对合理设计凝固过程和后续热处理工艺非常重要。中南大学Du等[48]基于所建立的热力学及热物性质数据库模拟计算了A356.1铝合金定向凝固(冷却速度为2 K/s)后的显微组织及成分偏析。在模拟计算时，考虑了固相、液相中的扩散、过冷及二次树枝晶的长大对凝固过程的影响。图13为定向凝固A356.1合金的显微组织。经EPMA成分分析，样品中存在的相有(Al)、(Si)、α-AlMnSi和β-AlFeSi。

图13　定向凝固A356.1合金的金相照片(冷却速度：2 K/s)[48]Fig.13　Metallograph in a transverse section of the A356.1 alloys directionally solidified with a cooling rate of 2 K/s[48]

采用BSE图像自动分析得到(Al)、(Si)、α-AlMnSi和β-AlFeSi相的体积分数分别为0.93、0.051、0.009和0.01。所测得的各相体积分数分别同计算预测结果 ((Al):0.93, (Si): 0.048,α-AlMnSi: 0.007,β-AlFeSi: 0.014)吻合较好。图14为应用3种模型模拟的Si在(Al)中的成分曲线与实验数据的比较。从图14可以看出，采用Gulliver-Scheil模型的模拟结果与实验数据相差较远，而采用球体模型和圆柱模型可以明显地改善模拟结果。这是因为Gulliver-Scheil模型仅考虑了热力学因素,而球体模型和圆柱模型同时考虑了热力学和动力学因素。

图14　定向凝固A356.1合金Si的成分曲线(冷却速度2 K/s)[48]Fig.14　Si concentration profile in the (Al) phase of theA356.1 alloy [48]

4.3数据库耦合相场法定量表征凝固过程微观结构演变

近20年来，相场法已成功应用于凝固过程等微观结构演变的模拟。实现微观结构演变的定量描述有3个要素：定量的相场模型,精准的热力学、热物性参数输入,关键的实测微观结构对模拟结果的验证。其中，精准的热力学、热物性参数输入是进行定量相场模拟的基础条件。最近，北京科技大学的Zhang等[49]耦合热力学、热物性质数据库与等温相场模型，定量模拟了Al-1.1%Cu-1.8%Mg合金的各向枝晶自由长大过程(如图15所示)，其中图15a和15b是模拟体系的温度场和相场,图15c和15d分别是固、液相中Cu和Mg的成分场。图16显示的是模拟区的潜热和热容分布。结果显示潜热和热容随

图15　模拟的Al-1.1%Cu-1.8%Mg合金枝晶生长过程(t=4.5×10-5s)[49]:(a)温度场,(b)相场,(c)cCu, (d)cMgFig.15　Simulation results of Al-1.1% Cu-1.8% Mg dendritic solidification process (t= 4.5×10-5 s)[49]: (a) temperature field, (b) phase field, (c) cCuand (d) cMg

图16　模拟的凝固时间为4.5×10-5 s的潜热(a)和热容(b)分布图[49]Fig.16　Simulated latent heat and heat capacity distributions at solidification time of 4.5×10-5 s[49]: (a) latent heat, (b) heat capacity

温度和成分变化而变化。如果没有热力学及热物性参数的输入，相场模型不可能定量描述凝固过程这些参量的变化。

5结语

建立高质量的热力学数据库和热物性质数据库并与相场方法相结合是实现多元多相铝合金制备过程微观结构演变定量描述的有效途径。其中精准的热力学、热物性参数输入是对微观结构进行定量描述的必备条件。经过约30年的发展，相图计算领域学者基于CALPHAD技术已构建了相对成熟的多元铝合金热力学数据库，在构筑扩散系数、粘度及摩尔体积等CALPHAD类型的热物性质数据库方向也有了许多突破。但仍然有以下一些问题亟待解决，这些问题的解决无疑将对多元铝合金热力学和热物性质数据库的进一步发展和完善起到重要作用。

(1)多元铝合金中常常通过添加一些高挥发元素(如Mg，Zn等)和高反应活性元素(如Sr，Ca等)来改善其性能。虽然样品制备方法上有了一定的突破，但采用CALPHAD技术构筑含这些元素的精确的多元铝合金热力学及热物性质数据库需要一系列新颖实验设备高效测定这类合金的热力学及热物性质。

(2)界面能是影响微观结构演变的重要热物性质，但由于实验测定上的难度导致界面能的获取任重而道远。

(3)多元铝合金中常常包含一些重要的亚稳相，由于实验很难测定亚稳相的相关信息，且理论计算相对复杂，目前国际上还缺乏关于亚稳相热力学及热物性质数据库的系统报道。

参考文献References

[1]Gottstein G.IntegralMaterialsModeling:TowardsPhysics-BasedThrough-ProcessModels[M]. Germany：Wiley-VCH Verlag GmbH & Co. KGaA, 2007: 17-32.

[2]Cicerone R J,Charles M C.IntegratedComputationalMaterialsEngineering:ATransformationalDisciplineforImprovedCompetitivenessandNationalSecurity[M]. Washington D C, USA: The National Academies Press, 2008.

[3]Olson G. Genomic Materials Design: The Ferrous Frontier [J].ActaMaterialia, 2013, 61: 771-781.

[4]Yang Rui(杨锐)，Chen Nanxian(陈难先)，Wang Chongyu(王崇愚)，etal.KeyProblemsonFundamentalScienceofMaterialsDesignBasedonIntegratedComputation(基于集成计算的材料设计基础科学问题)[R]. 973 项目，2011.

[5]Du Yong(杜勇)，Xu Honghui(徐洪辉)，Kong Yi(孔毅),etal. 多元Al合金的热力学和热物性数据库的建立及凝固过程显微组织演变的模拟 [J].MaterialsChina(中国材料进展), 2010, 29(6): 28-39.

[6]Thermo-Calc, http://www.thermocalc.com/.

[7]Pandat, http://www.computherm.com/pandat.html.

[8]Du Yong, Liu Shuhong, Zhang Lijun,etal. An Overview on Phase Equilibria and Thermodynamic Modeling in Multicomponent Al Alloys: Focusing on the Al-Cu-Fe-Mg-Mn-Ni-Si-Zn System [J].Calphad, 2011, 35: 427-445.

[9]Lu Xueshan(陆学善).PhaseDiagramsandPhaseTransformation(相图与相变) [M]. Hefei: Press of University of Science and Technology of China, 1990.

[10]Zhang Bizhou(张圣弼)，Li Daozi(李道子).PrincipleofPhaseDiagram,CalculationandApplicationinMetallurgicalProcess(相图原理、计算及在冶金中的应用)[M].Beijing: Metallurgical Industry Press,1986.

[11]Zhao Jicheng.MethodsforPhaseDiagramDetermination[M]. Oxford: Elsevier, 2007.

[12]Schuster J C, Pan Zhu, Liu Shuhong,etal. On the Constitution of the Ternary System Al-Ni-Ti [J].Intermetallics, 2007, 15: 1 257-1 267.

[13]Hao Dan, Hu Biao, Zhang Kai,etal. The Quaternary Al-Fe-Ni-Si Phase Equilibria in Al-Rich Corner: Experimental Measurement and Thermodynamic Modeling [J].JournalofMaterialsScience, 2014, 49:1 157-1 169.

[14]Zapolsky H, Pareige C, Marteau L,etal. Atom Probe Analyses and Numerical Calculation of Ternary Phase Diagram in Ni-Al-V System [J].Calphad, 2001, 25 (1): 125-134.

[15]Petzow G , Effenberg G.TernaryAlloys:AComprehensiveCompendiumofEvaluatedConstitutionalDataandPhaseDiagrams[M]. Germany: Weihheim: VCH, 1993.

[16]Wang Peisheng(王培生), Du Yong(杜勇), Zhou Hua(周华),etal.FabricationandThermalPropertyAnalysisMethodforMagnesiumAlloywithHighEvaporabilityandReactivityElements(含高挥发、高反应活性元素的镁合金制备及其热分析方法): China, 201410670337.3 [P]. 2014-12-01.

[17]Li Qian(李茜).PhaseEquilibria,ThermodynamicSimulationandItsApplicationinAl-Mg-Ce,Al-Mg-Zr,Al-Mg-Sc-ZnSystems(Al-Mg-Ce、Al-Mg-Zr和Al-Mg-Sc-Zn体系的相平衡、热力学模拟及应用)[D].Changsha：Central South University,2014.

[18]Kaufman L, Cohen L. The Martensitic Transformation in the Iron-Bickel System [J].TransAIMEJMetals, 1956, 206: 1 393-1 401.

[19]Wolverton C, Yan X-Y, Vijayaraghavan R,etal. Incorporating First-Principles Energetics in Computational Thermodynamics Approaches [J].ActaMaterialia, 2002, 50: 2 187-2 197.

[20]Wolverton C, Ozolinš V. First-Principles Aluminum Database: Energetics of Binary Al Alloys and Compounds [J].PhysicalReviewB, 2006, 73: 144 104/1-14.

[21]Liu Zi kui. First-Principles Calculations and CALPHAD Modeling of Thermodynamics [J].JournalofPhaseEquilibriaandDiffusion, 2009, 30 (5): 517-534.

[22]Golumbfskie W J, Arroyave R, Shin D,etal. Finite-Temperature Thermodynamic and Vibrational Properties of Al-Ni-Y Compounds via First-Principles Calculations [J].ActaMaterialia, 2006, 54: 2 291-2 304.

[23]Hu Gengxiang(胡赓祥),Cai Xun(蔡 珣).FundamentalsofMaterialsScience(材料科学基础)[M].Shanghai: Shanghai Jiaotong University Press, 2000.

[24]Andersson J-O , Ågren J. Models for Numerical Treatment of Multicomponent Diffusion in Simple Phases [J].JournalofAppliedPhysica, 1992, 72: 1 350-1 354.

[25]Cermak J, Rothova V. Concentration Dependence of Ternary Interdiffusion Coefficients in Ni3Al/Ni3Al-X Couples withX=Cr, Fe, Nb and Ti [J].ActaMaterialia, 2003, 51: 4 411-4 421.

[26]Cheng Kaiming, Chen Weimin, Liu Dandan,etal. Analysis of the Cermak-Rothova Method for Determining the Concentration Dependence of Ternary Interdiffusion Coefficients with A Single Diffusion Couple [J].ScriptaMaterialia, 2014,76: 5-8.

[27]Chen Weimin, Zhang Lijun, Du Yong,etal. A Pragmatic Method to Determine the Composition-Dependent Interdiffusivities in Ternary Systems by Using A Single Diffusion Couple [J].ScriptaMaterialia, 2014, 91:53-56.

[28]Chen Weimin, Zhang Lijun, Du Yong,etal. Viscosity and Diffusivity in Melts: from Unary to Multicomponent Systems [J].PhilosophicalMagazine, 2014, 94(14):1 552-1 577.

[29]Mantina M, Wang Y, Chen L Q，etal．First Principle Impurity Diffusion Coefficients [J].ActaMaterialia，2009，57: 4 102-4 108.

[30]Xin Jinghua, Zhang Weibin , Wang Jianchuan,etal. Prediction of Diffusivities in fcc Phase of the Al-Cu-Mg System: First-Principles Calculations Coupled with CALPHAD Technique [J].ComputationalMaterialsScience, 2014, 90: 32-43.

[31]Grover R, Getting I C, Kennedy C. Simple Compressibility Relation for Solids [J].PhysicalReviewB, 1973, 7:567-570.

[32]Lu Xiaogang, Selleby M, Sundman B. Implementation of A New Model for Pressure Dependence of Condensed Phases in Thermo-Calc[J].Calphad, 2005, 29(1): 49-55.

[33]Lu Xiaogang, Selleby M, Sundman B. Assessments of Molar Volume and Thermal Expansion for Selected bcc, fcc and hcp Metallic Elements [J].Calphad, 2005, 29(1): 68-89.

[34]Fernandez Guillermet A. Critical Evaluation of the Thermodynamic Properties of Cobalt [J].InternationalJournalofThermophysics, 1987, 8(4): 481-510.

[35]Liu X, Oikawa K. Assessment of the Temperature and Pressure Dependence of Molar Volume and Phase Diagrams of Cu and Zn [J].Calphad, 2014, 47: 114-122.

[36]Lu Xiaogang, Selleby M, Sundman B. Theoretical Modeling of Molar Volume and Thermal Expansion [J].ActaMaterialia, 2005, 53(8): 2 259-2 272.

[37]Lu Xiaogang， Chen Qing. A CALPHAD Helmholtz Energy Approach to Calculate Thermodynamic and Thermophysical Properties of fcc Cu [J].PhilosophicalMagazine, 2009, 89(25): 2 167-2 194.

[38]Brosh E, Makov G, Shneck R Z. Application of CALPHAD to High Pressures [J].Calphad, 2007, 31(2): 173-185.

[39]Karbasi A, Saxena S, Hrubiak R. The Thermodynamics of Several Elements at High Pressure [J].Calphad, 2011, 35(1): 72-81.

[40]Hallstedt B. Molar Volumes of Al, Li, Mg and Si[J].Calphad, 2007, 31(2): 292-302.

[41]Trybula M, Fima P, Gasior W. Thermodynamic Properties of Liquid Al-Li-Zn Alloys Determined from Electromotive Force Measurement [J].ThermochimicaActa, 2014, 588: 16-21.

[42]Moosavi M, Motahari A, Omrani A,etal. Thermodynamic Study on Some Alkanediol Solutions: Measurement and Modeling [J].ThermochimicaActa, 2013, 561: 1-13.

[43]Schick M, Brillo J, Egry I,etal. Viscosity of Al-Cu Liquid Alloys: Measurement and Thermodynamic Description [J].JournalofMaterialsScience, 2012, 47: 8 145-8 152.

[44]Lihl F, Nachtigall E,Schwaiger A.Viscosity Measurements on Binary Aluminum Alloys Containing Silicon, Zinc, Copper, and Magnesium [J].ZeitschriftfürMetallkunde, 1968, 59: 213-219.

[45]Gebhardt E, Detering K. Properties of Metallic Melts. XVI. Internal Friction of An Aluminum Alloy Eutectic [J].ZeitschriftfürMetallkunde, 1959, 50:379-385.

[46]Hekmat-Ardakan A, Ajersch F, Chen X.-Grant. Microstructure Modification of Al-17%Si Alloy by Addition of Mg [J].JournalofMaterialsScience, 2011, 46: 2 370-2 378.

[47]Hekmat-Ardakan A , Ajersch F. Thermodynamic Evaluation of Hypereutectic Al-Si (A390) Alloy with Addition of Mg [J].ActaMaterialia, 2010, 58: 3 422-3 428.

[48]Du Yong, Chang Y Austin, Liu Shuhong,etal. Thermodynamic Description of the Al-Fe-Mg-Mn-Si System and Investigation of Microstructure and Microsegregation during Directional Solidification of An Al-Fe-Mg-Mn-Si Alloy[J].ZeitschriftfürMetallkunde, 2005, 96: 1 351-1 362.

[49]Zhang Shuzhou, Zhang R, Qu Xuanhui,etal. Phase Field Simulation for Non-Isothermal Solidification of Multicomponent Alloys Coupled with Thermodynamics Database [J].TransactionsofNonferrousMetalsSocietyofChina, 2013, 23: 2 361-2 367.

(编辑惠琼)

专栏特约编辑杜　勇

杜勇:男，1964年生，中南大学教授、博士生导师，中德“铝合金微结构”联合实验室主任；国家杰出青年科学基金获得者，教育部长江学者，国家自然科学基金委员会创新研究群体负责人。现任国际刊物CALPHAD,JPhaseEquilibDiff副主编，IntJMaterRes(原德国金属学报)，Vacuum，JMiningandMetallurgy等杂志编委，国际相图委员会委员。主持国家自然科学基金创新研究群体和重点项目、“863”、重大国际合作等项目28项；获省自然科学一等奖1项，国家自然科学三等奖1项，省科技进步二等奖1项，国际相图委员会最佳论文奖1项，获授权发明专利2项；先后在ActaMater,PhysRevB等30种国际刊物上发表论文320篇，SCI

特约撰稿人Hans Juergen Seifert

他引近3 000次，美国、德国出版的4种专著中用多达400个版面收录其研究结果。解决构筑多元多相材料热力学/动力学数据库等的系列重要科学问题，建立了国际上迄今最准确的铝合金热/动力学数据库和世界上第二个硬质合金热/动力学数据库。累计在国际会议作大会/主题报告42次，作为大会主席组织2次中德热/动力学及其在凝固过程中应用的国际会议；2014年与金展鹏院士共同组织了第43届CALPHAD国际会议。

Hans Juergen Seifert:现为德国卡尔斯鲁厄理工学院材料科学与工程系主任、应用材料物理研究所教授，美国佛罗里达大学材料科学与工程系兼职教授。1993年于斯图加特大学获材料科学博士学位。1999年获得德国材料科学学会

特约撰稿人商顺利

马兴纪念奖。2001年至2003年任阿尔斯通电力公司(瑞士)有限公司高级涂料专家；2003年至2006年任佛罗里达大学助理教授；2006年7月至2012年任德国弗莱贝格矿业和技术大学应用材料科学系教授。研究领域涵盖材料热力学和化学，包括相变动力学，涉及金属合金、先进陶瓷及其复合材料。拥有2项欧洲专利和1项美国专利，出版20本专著和手册章节，在国际期刊和会议发表论文100余篇。多次组织热力学建模和应用国际研讨会。两次到中南大学开展合作科研。

商顺利：男，1972年生，高级研究助理。2000年北京有色金属研究总院博士毕业，2001~2005年在荷兰代尔夫特科技大学从事博士后研究，2005年至今在美国宾夕法尼亚州立大学研究、

特约撰稿人刘树红

作。2008年获宾夕法尼亚州立大学Rustum & Della Roy材料研究创新奖。美国自然科学基金和美国能源部等研究项目的负责人(PI)或共同负责人(Co-PI)。主要研究领域包括金属和能源材料的热力学、扩散和力学性能的第一原理计算，温度与成分相关的相稳定性，以及极化和非极化材料的第一原理声子计算。发表140余篇国际期刊论文和12篇会议论文，其中有7篇论文发表在影响因子大于4的期刊上，有40篇论文发表在影响因子为3~4的期刊上。科学引文数据库Web of Science (即SCI)的研究人员识别号为A-6564-2009，Google Scholar的为hE7IaIEAAAAJ。Web of Science收录130篇论文，H-index为23；Google Scholar H-index 是26。担任超过15个国际刊物的审稿人。

刘树红：女，1981年生，副研究员，硕士生导师。2010年6月获得博士学位。2006年5月至9月在维也纳大学物理化学研究所从事合作科研，参加中-奥(地利)联合项目。2010年12月~2011年11月赴德国亚琛工业大学材料系从事博士后研究。截至目前，已在Calphad,JAlloysCompds,IntJMaterRes等国际期刊发表或合作发表学术论文60余篇。其中，发表在Intermetallics上的一篇论文获2007年度国际相图委员会最佳论文奖。担任Calphad和JAlloysCompds等国际期刊的审稿人。参与完成的“铝合金热力学及原子移动性的理论及应用”项目获2010年湖南省科学奖一等奖(排名第四)。主持自然科学基金项目2项，参与国家自然科学基金面上项目、重点项目，“973”项目各1项。参与开发的多元铝合金相图热力学数据库(TCAL3)被材料设计领域世界领先的Thermo-Calc 公司评价为国际上罕见的高质量数据库并在全世界范围内推广使用。主要研究方向：相图热力学实验测定及计算模拟；热物性质计算模拟。

Thermodynamic and Thermophysical Databases ofMulticomponent Al Alloys and Their Applications

LIU Shuhong, LING Dicheng, HUANG Dandan, ZHANG Fan, DU Yong

(State Key Laboratory for Powder Metallurgy, Central South University, Changsha 410083,China)

Abstract：Thermodynamic properties and phase equilibria are prerequisite for understanding many scientific and technological disciplines. Accurate databases for thermodynamic and thermophysical properties are the key to realize the description of microstructure evolution of multicomponent and multiphase alloys. As super-structural materials for aerospace and civil industry, the optimal process for the aluminum alloys is very important and has received a lot of concerns. This paper firstly provides an overview on the thermodynamic database and the latest research progress on the multicomponent aluminum alloys, especially introducing the application of TEM and 3DAP in the measurement of phase equilibria of the multicomponent alloys as well as the importance of first-principles calculations in the construction of the thermodynamic database. Subsequently, a brief introduction about the recent research on the thermophysical databases of the aluminum alloys, such as diffusion coefficient, molar volume as well as the viscosity, is presented. Then three case studies are described to show how the thermodynamic and thermophysical databases are applied in the simulation of the solidification microstructure of the aluminum alloys. Finally, the major challenges for the development of accurate thermodynamic and thermophysical databases for multicomponent and multiphase aluminum alloys are briefly concluded.

Key words：Al alloys; phase equilibria; thermodynamic database; thermophysical properties; CALPHAD technique

中图分类号：TG146.2

文献标识码：A

文章编号：1674-3962(2015)04-0305-11

DOI:10.7502/j.issn.1674-3962.2015.04.07

通讯作者：第一作者及刘树红，女，1981年生，副研究员，硕士生导师，Email：shhliu@csu.edu.cn

基金项目：国家自然科学基金资助项目(51101172); 科技部973计划项目(2011CB610401,2014CB6644002);中德“铝合金微结构”联合实验室(GZ755)

收稿日期：2014-12-30