覆盖粗糙集的偏序关系研究

单雪红，吴 涛，张文军，高显彩

1.宿州学院 数学与统计学院，安徽 宿州 234000

2.安徽大学 数学科学学院，合肥 230039

3.宿州二中，安徽 宿州 234000

1 引言

粒计算通过对现实问题进行多角度、多层次的描述和理解，从而得到问题的粒结构表示，是研究复杂问题求解、海量数据的挖掘和不精确、模糊信息处理等的有效工具[1]。粒化是粒计算的基本问题之一，在粒计算的研究中，根据问题粒化得到的粒子间是否存在交集，将它们分别称为覆盖粒计算模型和划分粒计算模型[1]，其中划分粒计算模型，由于具有较好的理论基础而被广泛地研究。如经典的粗糙集理论就属于划分粒计算模型的研究范畴[2-3]。经典粗糙集理论是基于等价关系的硬划分，即它的知识为论域上的划分，也即知识中的概念之间不存在交集[2]，但在许多实际的应用中，知识中的概念一般都会存在交叉，所以基于等价关系的划分要求就过于严格，这样就限制了粗糙集的发展，所以有必要将粗糙集理论推广到更一般的形式。基于覆盖的粗糙集模型是经典粗糙集模型的推广，由于更具有一般性，近年来受到研究者的关注，并取得了一定的研究成果[4-12]。

关于覆盖粒度空间的层次模型研究，给出合理的偏序较细关系是关键，已有一些学者对该问题做了一些尝试。Huang等[11]，Zhang等[12]分别定义了两种不同的覆盖上的偏序较细关系。随后Hu等人分析发现以上两种偏序较细关系都存在问题，对其进行了改进，提出了新的定义。但是，分析发现，Hu等[13]人提出的覆盖上的偏序较细关系也不满足覆盖近似空间下的概念近似具有偏序关系是覆盖近似空间本身具有偏序较细关系的充要条件，因此，本文重新定义了覆盖上的偏序较细关系，并对其性质进行了研究，证明了该定义满足覆盖近似空间下的概念近似具有偏序关系是覆盖近似空间本身具有偏序较细关系的充要条件。

2 基本概念

为了进行比较分析，先介绍覆盖近似空间的相关概念和已提出的三种偏序关系的定义。

定义1[4]设U是非空有限论域，C是U的一个子集族，如果∪C=U且C≠Ø，则称C是U的一个覆盖，称有序对(U，C)为覆盖近似空间。

定义3[13]设(U，C)为覆盖近似空间，对于任意集合X⊆U，也称为U中的一个概念，则有下列定义：

因为划分是一种特殊的覆盖，所以Pawlak近似空间是覆盖近似空间的一种特殊情况，当覆盖近似空间退化为Pawlak近似空间时，覆盖粗糙集模型也将退化为经典的粗糙集模型，因此覆盖粗糙集模型是经典粗糙集模型的扩展[13]。

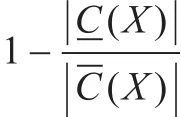
粗糙度ρC(X)的大小，反应了近似空间对X的刻画能力的强弱。

一般的，若近似空间(U，C1)较近似空间(U，C2)更细，则近似空间(U，C1)对概念X⊆U的刻画能力较近似空间(U，C2)更强，反之亦然，因此，可得覆盖粒度空间上较细关系的3条公理[13]。

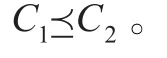
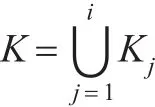
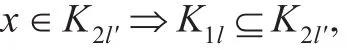
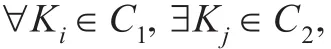
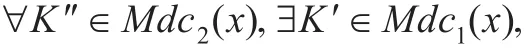
通过分析研究，发现Hu等人给出的第三种偏序较细关系的定义并不满足公理1，如下例：

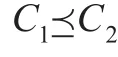
3 新的覆盖上的偏序较细关系

根据上例的分析，加上Hu等人的分析，以上三种覆盖上的偏序较细关系的定义都存在不合理之处，因此重新给出了一种偏序较细关系的定义。

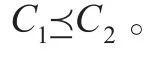
该定义可直观描述为对粒度较大的覆盖块进行了软划分。

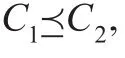
(⇐)假设C1C2不成立，根据定义 9，则 ∃x∈U，K1∈Mdc1(x)，对 ∀K2∈Mdc2(x)，有，则K1与 ∀K2有以下两种关系：K1∩K2=Ø（因为x∈K1且x∈K2，所以K1∩∀K2=Ø是不可能的，K1与K2仅相交，除K2⊂K1），或者K2⊂K1。显然，K2在 (U，C2)下有K2，（1）若K1∩K2≠Ø，在 (U，C1)下，因为，所以（与条件矛盾）；（2）若K2⊂K1，在 (U，C1)下，即，因而（与条件矛盾）。

综上可知，有C1C2成立，因此必要性成立。

定理2设C1和C2是非空论域U上的两个覆盖，C1C2当且仅当在覆盖近似空间 (U，C1)和 (U，C2)下，对于∀X⊆U，有

证明(⇒)设C1C2，则对 ∀K1∈Mdc1(x)，都 ∃K2∈Mdc2(x)，使得K1⊆K2，对 ∀X⊆U，若K1∩X≠Ø，则K2∩X≠Ø，即，因此有。

定理1和定理2说明本文定义的覆盖粒度空间的较细关系满足公理1和公理2，这与人们对粒度的认知直觉是一致的。

4 结束语

覆盖粒度空间的层次模型研究，关键是给出合理的偏序较细关系，现有的偏序较细关系定义都有其不足的地方。本文给出了一种新的偏序较细关系的定义，并证明其与覆盖近似空间下的概念近似偏序关系是等价的。这些研究结果为实际问题的应用提供了理论依据。

[1]苗夺谦，王国胤，刘清，等.粒计算：过去、现在与展望[M].北京：科学出版社，2007.

[2]Pawlak Z.Rough set[J].International Journal of Computer Information Sciences，1982，11（5）：342-356.

[3]Yao Y Y.A partition model of granular computing[J].LNCS Transactions on Rough Sets，2004（1）：232-253.

[4]Bonikowski Z，Bryniarski E，Wybraniec U.Extensions and intentions in the rough set theory[J].Information Sciences，1998，107（1）：149-167.

[5]Wang Shiping，Zhu Qingxin，Zhu William，et al.Quantitative analysis for covering-based rough sets through the upper approximation number[J].Information Sciences，2013，220（8）：483-491.

[6]Zhu W，Wang F Y.Reduction and axiomization of covering generalized rough sets[J].Information Sciences，2003，152（1）：217-230.

[7]Zhu W，Wang F Y.A new type of covering rough set[C]//The 3rd International IEEE Conference Intelligent Systems，2006：444-449.

[8]Zhu W，Wang F Y.The fourth type of covering-based rough sets[J].Information Sciences，2012，201（2）：80-92.

[9]Zhu W.Topological approaches to covering rough sets[J].Information Sciences，2007，177（6）：1499-1508.

[10]Hu J，Wang G Y，Zhang Q H.Covering based generalized rough fuzzy set model[J].Journal of Software，2010，21（5）：968-977.

[11]Huang B，He X，Zhou X Z.Rough entropy based on generalized rough sets covering reduction[J].Journal of Software，2004，15（2）：215-220.

[12]Zhang Q H，Wang G Y，Hu J，et al.Approximation partition spaces of covering space[C]//IEEE International Conference on Granular Computing，Silicon Valley，2007：199-204.

[13]Hu J，Wang G Y.Hierarchical model of covering granular space[J].Journal of Nanjing University：Natural Sciences，2008，44（5）：551-558.