颜色共生矩阵的Fisher信息度量及识别应用

张 玥，刘传才，邹 健，卢桂馥

1.南京理工大学 计算机学院，南京 210094

2.安徽工程大学 应用数理学院，安徽 芜湖 241000

3.安徽工程大学 计算机信息学院，安徽 芜湖 241000

1 引言

颜色、纹理和形状是用以描述图像属性的最基本底层特征，广泛应用于目标识别任务[1-8]。鉴于颜色对目标的尺度、旋转和姿态变化鲁棒，并能适应一定的视点变化，因此，与灰度图像相比，彩色图像的颜色特征能提供更丰富且鲁棒的鉴别信息[2]。纹理是图像的一种区域性特征，它在图像上表现为灰度或颜色分布的某种规律性，通常被用来描述目标表面的粗糙程度和它的方向性的规律性。由Haralick[1]最先引入的灰度共生矩阵（GLCM）是最经典的灰度纹理特征，它以统计的方式描述了图像局部结构给定条件下像素灰度水平二维联合分布，能较好地反映像素灰度水平的相关性规律和灰度空间的依赖关系。尽管彩色图像含有丰富的视觉特征，但是很多现有技术对图像颜色信息的利用是在忽略空间相关性的情形下突出对一些全局特征使的应用，而对于纹理信息的使用则是在忽略像素颜色的前提下强调图像局部邻域内像素强度值的空间信息。从视觉识别技术的发展进程来看，在一个识别系统中整合和利用不同类型特征的互补信息已成为一种趋势[4，7]。新近的研究表明，在各种形式的底层特征融合方案中，颜色和纹理特征的融合通常具有高效率和强鉴别性[4，7-8]。

Palm[7]首先采用共生矩阵方法整合图像中颜色和纹理信息，并将颜色共生矩阵根据颜色通道的组合方式分为单通道颜色共生矩阵和多通道颜色共生矩阵。其中，单通道颜色共生矩阵仅是从单个颜色通道图像上提取的类似于GLCM的描述子，不含不同通道颜色的空间相关性；多通道颜色共生矩阵通过对不同通道颜色的空间相关性的量化对图像的颜色和纹理属性加以概括。鉴于颜色共生矩阵具有非线性拓扑结构，这导致了使用从颜色共生矩阵中进一步提取的Haralick特征的方法十分流行，显然这种方法的缺陷是无法利用共生矩阵中完整的统计信息[1，4，7-8]。

根据颜色共生矩阵的自然形式，本文提出在共生矩阵流形上借助从多项流形中诱导的费歇尔-黎曼（Fisher-Riemannian）度量量化不同目标图像共生矩阵间的信息差异的方法并将其应用于彩色目标识别。就RGB彩色图像而言，在颜色量化水平和每个像素局部邻域给定的条件下，该方法将一幅图像各个通道图像对上共生的颜色建模为六个潜在的多项分布的概率实现，而提取的六个归一化的颜色共生矩阵（单通道和多通道类型各三个）可视为潜在模型参数的基于最大似然估计的矩阵化形式。因此，两幅图像的相似性度量就可以通过量化六个颜色共生矩阵的信息差异实现。在采用紧化的共生频率嵌入并对每个因子流形赋予诱导的多项Fisher信息距离度量条件下，积形式的颜色共生矩阵流形提供了差异量化的几何平台。在识别应用中，考虑到每个因子流形上共生信息差异的权重不同，提出的方法先在每个因子流形上使用最近邻分类器进行标签预测，然后在积流形上通过多数投票完成测试样本与训练样本间的匹配。实验表明，针对彩色目标的识别，与经典的Haralick特征方法和子空间方法相比，该方法在识别精度上能获得较大的优势。

2 颜色共生矩阵及基于颜色共生模型的目标表示

假设I是大小为m×n的RGB彩色图像，用IR、IG、IB分别表示R、G、B三颜色成分（通道）图像，并把它们构成的集合记为 I={IR，IG，IB}。在给定了设置：（1）量化R、G、B颜色W-水平集={0，1，…，W-1}；（2）由像素间距离d和若干方向θ∈Θ确定像素邻域结构{(d，θ):θ∈Θ}；（3）由两个单通道颜色图像组成的图像对(Iu，Iv)∈I×I，定义关于图像对 (Iu，Iv)的颜色共生矩阵为量化颜色为条件概率分布：

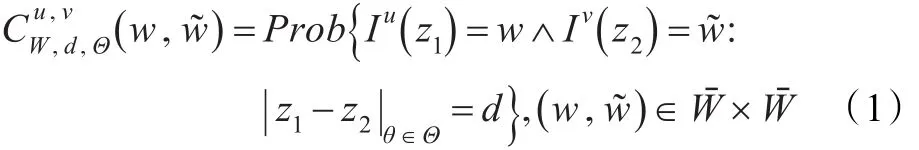
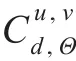
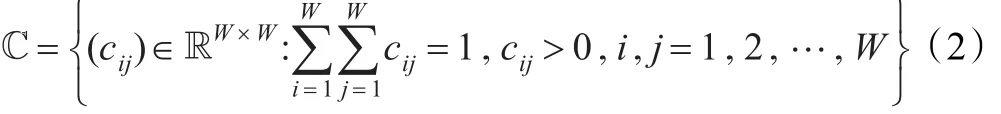
这样，在上述设置下一幅RGB彩色图像的任意一对通道图像上共生颜色的概率生成模型可视为 中的一点。考虑到多项分布族[9]：

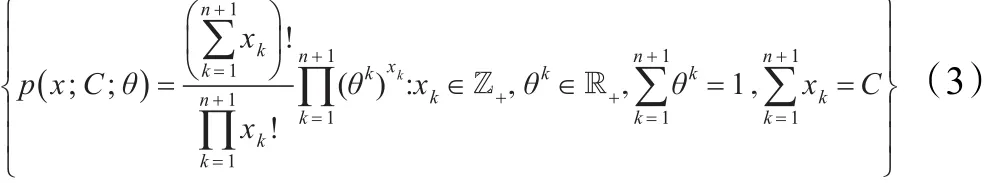
的参数空间：

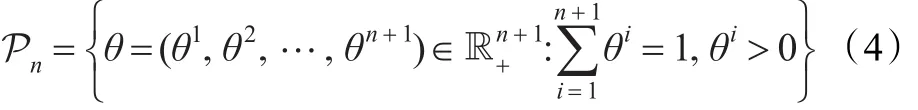
在赋予了费歇尔-黎曼结构时[10-11]，可以导出闭式表达的Fisher信息距离（即测地距离）度量：

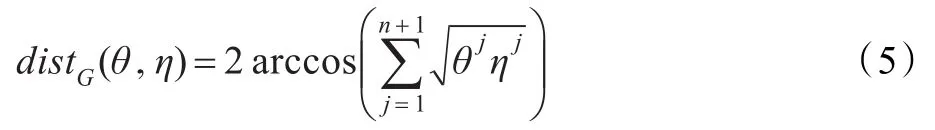
因此，颜色共生矩阵的模型空间ℂ可以自然地从PW2-1上诱导Fisher信息距离度量：

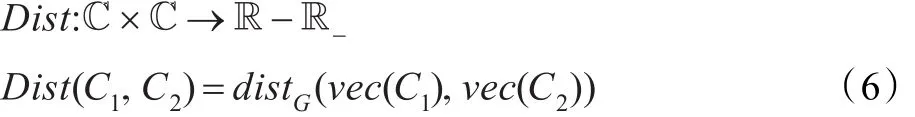
其中vec(⋅)是对矩阵向量化算子。本文将配备了信息度量Dist的模型空间ℂ称为共生矩阵流形。显然，三种常见的颜色通道策略[7]对应着三个乘积共生矩阵流形框架下的目标表示法：

（1）单通道策略（SCM）：图像中的目标按三个单通道颜色共生模型表示为ℂ3中的一点。

（2）多通道策略（MCM）：图像中的目标按三个多通道颜色共生模型表示为ℂ3中的一点。

（3）单、多通道混合策略（SCM+MCM）：图像中的目标按六个颜色共生模型表示为ℂ6中的一点。

本文将ℂ3和ℂ6均称为积颜色共生矩阵流形，ℂ为其因子流形。

3 嵌入及基于多数投票的目标匹配

鉴于共生矩阵内在的非欧结构，在基于颜色共生矩阵的识别方法中，研究者往往先对每个颜色共生矩阵进一步提取像对比度、同质性、相关性、相异性、能量、熵等经典特征并对所有考虑的颜色通道将这些特征作成加长向量，然后使用适当的分类器实现识别[7]。毫无疑问，这些方法以牺牲共生矩阵中部分鉴别信息为代价。从分布的特性考虑，尽管Kullback-Leibler距离和Hellinger距离度量可用以共生信息的差异量化，但本文更倾向于使用能反映颜色共生矩阵流形上模型间内在几何结构的测地线距离作为匹配度量。实际上，测地距离作为统计流形上最自然的度量，除了用于分类外，还经常用于聚类、降维及分割等任务。在识别应用中，等式（1）中颜色共生概率均是未知的，且基于离散的颜色量化从图像中抽取的归一化颜色共生矩阵往往含多个零共生频率。为此，本文采用紧致化嵌入：

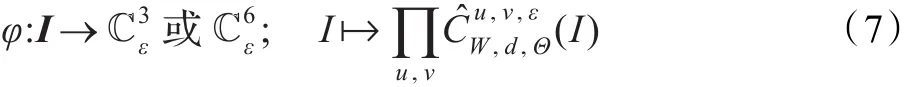
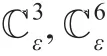
已有的研究表明，图像的不同通道图像对上的共生信息的鉴别性既存在显著差异，又具有一定互补性[4，7]。根据上述框架，本文提出的识别方法先在或的每个因子流形上借助基于度量Dist的最近邻分类器对测试样本和训练样本作匹配识别，然后对每个测试样本根据其在各个因子流形上获得的预测标签按多数投票的方式确定最终的类别，对于涉及票数最多的标签出现在多于一类的情形，按照随机方式决定其所属类。

4 实验结果及分析

为了验证由共生矩阵内几何导出的Fisher信息度量及投票策略在彩色目标识别任务中的有效性，选择Georgia Tech（GT）彩色人脸库[12]和 COIL-100目标库[13]进行识别实验。两个图像库所有图像均被裁割成64×64尺寸大小。为了对图像上的共生颜色进行计数和信息量化，采用32-水平颜色量化法，即W=32；d=1及Θ={kπ/4:k=0，1，2，3} 的局部像素邻域；另外，在使用rounding平滑技术时舍入参数ε设置为0.000 1。

GT人脸库包含50个个体的750张彩色人脸图像（每人15张），这些图像有着较大的姿态、表情和光照变化，图1展示了GT库7个个体的样本图像。

图1 GT人脸库中7个个体的样本图像

考虑到除了共生矩阵方法外，通过Gabor小波变换将一幅图像分解成一组滤波图像是另一种图像纹理描述的经典方法。为此，对于GT库上的人脸识别实验，选择使用本文提出的三种匹配策略：SCM、MCM和SCM+MCM对应的识别方法与基于Haralick特征的方法[7]（记为HFM）、以及三个基于多通道Gabor幅值的子空间方法：Gabor+PCA[14]、Gabor+LDA[14]、Gabor+LPP[15]进行识别性能比较。这里采用的子空间方法是将每幅人脸图像经40通道Gabor滤波变换生成的40通道幅值图像在采用r=2×2=4的下采样（为了有效地存储）条件下串连每张幅值图像上的幅值特征作成的向量应用到PCA、LDA和LPP（局部投影保持）三种算法进一步提取低维特征。其中，40通道的Gabor滤波器的参数设置与文献[5]的实验中采用的设置一致。对该库人脸的识别，采用10重交叉验证的识别方法，即执行每一重识别任务时，随机选取每人的k(k=3，4，5)张图像为训练样本，其余的作测试样本，表1显示了各种算法的平均识别率及对应的均方差。

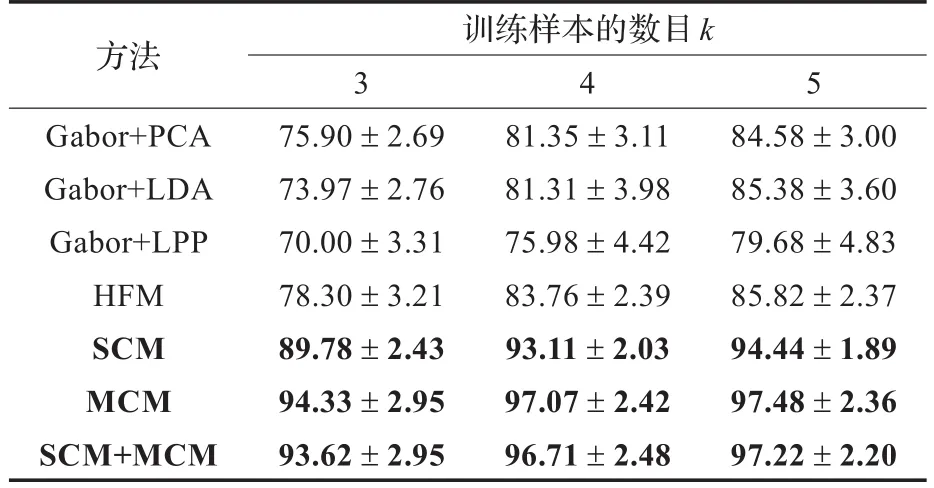
表1 本文提出的三种匹配方法与其他纹理方法在GT彩色人脸库上的平均识别率及均方差 %

从表1可以看到，三种综合通道信息的匹配策略的识别率（以黑体显示）以较大优势胜过其他方法。这主要得益于共生矩阵流形上的每个因子流形的费歇尔-黎曼几何高效地整合了图像中颜色和纹理的鉴别信息。另外，因子流形上的投票也使得各个颜色通道对上互补的颜色共生信息得以很好利用。在三种匹配策略中，多通道匹配策略（MCM）比单通道匹配策略（SCM）在识别中表现更为出色。尽管综合匹配策略（SCM+MCM）同时采用了单通道和多通道共生的空间信息，但它在识别时没有展现出显著的优势，其识别性能仅仅略微地优于单通道策略。基于Haralick特征的最近邻匹配算法取得了仅次于本文方法的识别性能。在使用较少训练样本(k=3，4，5)的情形下，尽管作为一种非监督的降维方法，Gabor+PCA获得了与监督方法Gabor+LDA可比较的识别结果，二者的识别性能均优于Gabor+LPP。对于任意一幅尺寸为m×n的RGB彩色图像，从中抽取一个w-水平的颜色共生矩阵的计算复杂度为O(mn)，而对相同尺寸的灰度图像施行Gabor卷积得到一幅幅值图像的计算复杂度为O(abmn)，其中a和b为Gabor卷积模板的尺寸。鉴于三种子空间方法在实施特征匹配前仍需对串连的幅值向量通过学习降维，而HFM方法在实施特征匹配前仍需进一步提取Haralick特征，因而本文提出的方法与这些方法相比在计算上涉及更低的复杂度。

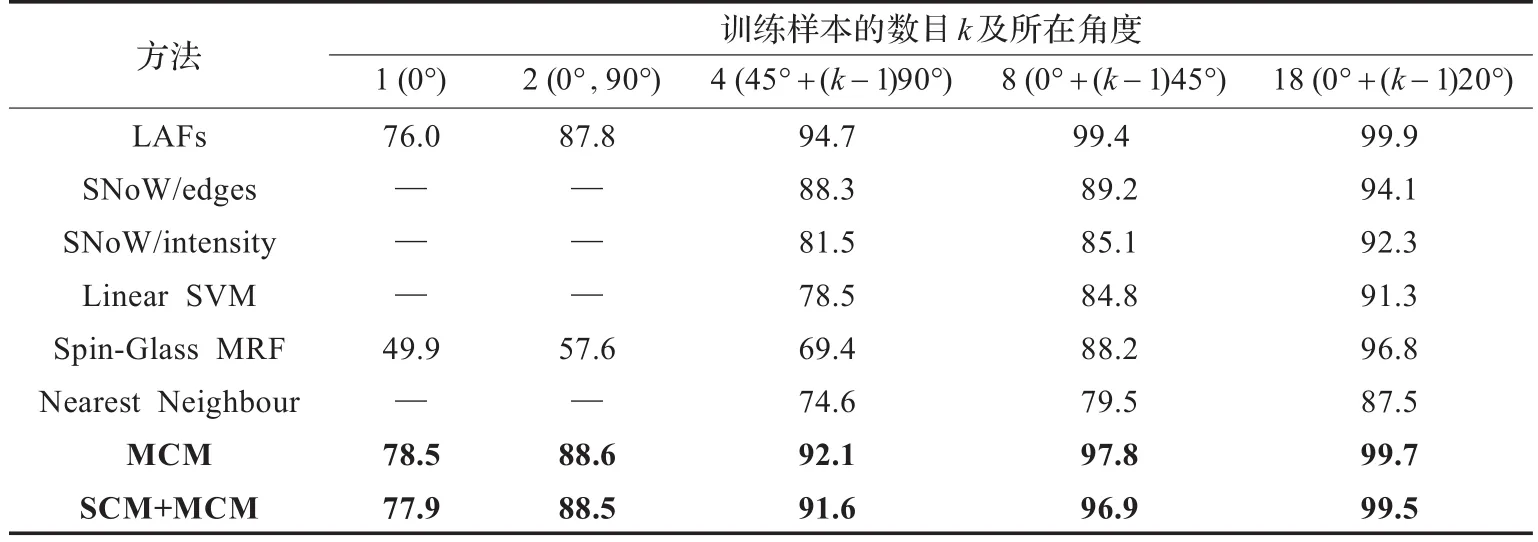
表2 本文提出的方法与其他方法在COIL-100彩色目标库上的识别率%

COIL-100目标库是一个包含100目标的7 200张彩色图像的目标库，图像目标被放置在一个处于黑色背景的转盘上，转盘相对于一个固定的摄像机每转动5°来改变目标的姿态，由此得到每个目标的72幅图像。图2展现了该库部分目标的样本图像。

图2 COIL-100目标图像库上的样本图像

在这个目标库上，将本文提出的基于MCM和SCM+MCM颜色共生信息匹配方法与文献[16]的实验报告中涉及的方法加以比较。为此，从每个目标的72张图像中抽取等视角点处的k(k=1，2，4，8，18)张作为训练样本并将剩余图像留作测试。表2展现了实验所得的识别率。

从表2可以看到，按照识别结果，本文方法在5种实验 情 形 下 优 于 SNoW/edges、SNoW/intensity、Linear SVM、Spin-Glass MRF和 Nearest Neighbour这5种方法。尽管LAFs在4、8和18个训练样本的识别实验中取得了比本文方法更高的识别率，但本文方法在小样本（单个和两个训练样本）情形下获得了更高的识别精度。关于本文的两种方法，基于多通道颜色共生信息匹配在识别性能上以微弱优势比混合匹配方法表现得更为出色。

5 结束语

在给定颜色量化和像素局部邻域结构条件下，本文提出的方法将图像上共生的颜色假设为积共生矩阵流形上一个潜在模型的概率实现。通过基于紧化的共生频率嵌入，将每幅图像视为紧化的积共生矩阵流形中的一点，且对每个因子流形赋予从多项流形上诱导的Fisher信息距离度量。在识别应用中，使用基于每个因子流形上最近邻分类器对投票方法。在GT彩色人脸库和COIL-100目标库上获得较好的实验结果证实了这种方法的可行性和有效性。

[1]Haralick R M，Shangmugam K，Dinstein I.Textural feature for image classification[J].IEEE Trans on Systems，Man，Cybernetics，1973，3（6）：610-621.

[2]Huang J，Kumar S R.Image indexing using color correlograms[C]//IEEE Conference on Computer Vision and Pattern Recognition，Puerto Rico，1997：622-768.

[3]张晗，何东健.一种融合纹理信息与图论的图像分割方法[J].计算机工程与应用，2014，50（1）：180-184.

[4]Losson O，Porebski A，Vandenbroucke N，et al.Color texture analysis using CFA chromatic co-occurrence matrices[J].Computer Vision and Image Understanding，2013，117（7）：747-763.

[5]Zhang Y，Liu C C.Gabor feature-based face recognition on productGammamanifold viaregionweighting[J].Neurocomputing，2013，117（6）：1-11.

[6]Yu L，He Z，Cao Q.Gabor texture representation method for face recognition using the Gamma and generalized Gaussian models[J].Image and Vision Computing，2010，28（1）：177-187.

[7]Palm C.Color texture classification by integrative co-occurrence matrices[J].Pattern Recognition，2004，37（5）：965-976.

[8]徐少平，李春泉，胡凌燕.一种改进的颜色共生矩阵纹理描述符[J].模式识别与人工智能，2013，26（1）：90-98.

[9]Merran E，Nicholas H，Brian P.Statistical distributions[M].3rd ed.New York：Wiley，2000：134-136.

[10]Lebanon G.Riemannian geometry and statistical machine learning[D].[S.l.]：Carnegie Mellon University，2005.

[11]Pennec X.Probabilities and statistics on Riemannian manifolds：basic tools for geometric measurements[C]//Proc of Nonlinear Signal and Image Processing（NSIP’99），Antalya，Turkey，1999：194-198.

[12]Georgia Tech face database[EB/OL].[2013-10-20].http：//www.anefian.com/research/face_reco.htm.

[13]COIL-100 database[EB/OL].[2013-10-20].http：//www1.cs.columbia.edu/CAVE/publications/pdfs/Nene_TR96_2.pdf.

[14]Van der Maaten L J P，Postma E O，van den Herik H J.Dimensionality reduction：a comparative review，Technical report 2009-005[R].Tilburg，The Netherlands：Tilburg Centre for Creative Computing，Tilburg University，2009.

[15]He X，Niyogi P.Locality preserving projections[C]//Advances in Neural Information Processing Systems，2004，16（1）.

[16]Obdrzalek S，Matas J.Object recognition using local affine frames on distinguished regions[C]//Proceedings of the British Machine Vision Conference，2002.