抗HIV感染治疗模型及临床数据模拟
孙起麟 ,闵乐泉 ,2
1.北京科技大学 自动化学院,北京 100083
2.北京科技大学 数理学院,北京 100083
1 引言
据世界卫生组织2014年7月发布的艾滋病(AIDS)疫情报道:艾滋病仍然是一个严重的全球公共健康问题,截至目前全世界共有超过3 900万人感染过艾滋病病毒(HIV);在2013年中,全球共有150万人死于艾滋病;有效的抗逆转录病毒药物治疗能够控制病情,使得HIV感染者可以享有健康的生活[1]。
数学模型已经成为病毒感染动力学研究中重要的研究工具,用以做出假设,提出新的实验,或者对复杂过程进行简单解释[2]。例如,数学模型能够对病毒载量在体内变化的动力学进行合理解释分析,并且在深入了解疾病和药物治疗中起到重要作用[3]。
Nowak等提出的病毒感染动力学模型已经被广泛用于研究HIV感染动力学[4-6]:

其中x,y和v分别表示未感染CD4+T细胞计数,已感染CD4+T细胞计数和HIV病毒载量。λ为未感染CD4+T细胞固有生成率;dx为未感染CD4+T细胞凋亡率;βxv为未感染CD4+T细胞被病毒感染的速率;ay为已感染CD4+T细胞凋亡率;ky为已感染CD4+T细胞产生病毒的复制率。uv为病毒的死亡率。这里λ,d,β,a,k,u均为正常数。
模型式(1)有两个平衡点:病毒清除平衡点和持续带毒平衡点。模型式(1)的基本再生数为:R0=λβk/dau,表示一个已感染CD4+T细胞在生命周期内复制释放出新病毒感染的靶细胞总数。当R0≤1,则模型式(1)的病毒清除平衡点全局渐近稳定;当R0>1,则模型式(1)的持续带毒平衡点全局渐近稳定[7]。
在模型式(1)的基本再生数R0中,λ/d代表人体内未感染CD4+T细胞的总数,这就意味着体内CD4+T细胞总数越大的人越难以治愈。显然模型式(1)导出的基本再生数R0不合理,因此需要对模型式(1)进行修正。为此,文献[8]提出了运用饱和发生率βxv/(x+v)替换病毒感染模型的双线性发生率βxv,修正模型的基本再生数R0与靶器官细胞总数无关。
在模型式(1)中未感染CD4+T细胞的凋亡率dx表示CD4+T细胞凋亡仅与人体固有的细胞生命周期相关。然而,HIV能够通过不同的机制分别诱导CD4+和CD8+T细胞凋亡[9]。而且,一定比例的CD4+T细胞被诱导凋亡说明HIV诱导凋亡可能是导致CD4+T细胞数量减少的一个重要机制;此外,HIV诱导CD4+T细胞凋亡的机制直接与病毒载量和CD4+T细胞计数相关[10]。基于上述讨论,本文假设模型式(1)中的CD4+T细胞凋亡率dx被替换为dx(1+k1v),该修正凋亡率包含CD4+T细胞固有凋亡和有HIV诱导CD4+T细胞凋亡机制。
2 抗HIV感染治疗模型
基于模型式(1),本文运用文献[8]提出的饱和发生率βxv/(x+v)和含有细胞凋亡诱导机制的凋亡率dx(1+k1v)得到一个改进的HIV感染模型:
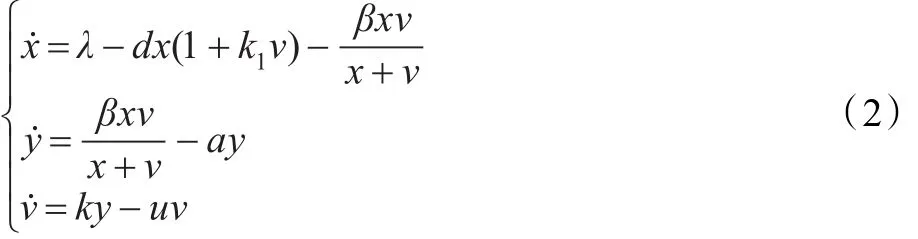
其中变量x,y,v和参数λ,d,β,a,k,u的含义与模型式(1)相同。k1为HIV诱导细胞凋亡的诱导率。
目前,抗病毒药物在对HIV病毒的抑制方面起到不可忽视的作用,已研发出治疗HIV的药物有逆转录酶抑制剂和蛋白酶抑制剂;逆转录酶抑制剂和蛋白酶抑制剂分别作用在β和k[11]。因此,模型式(2)所对应的抗HIV感染治疗模型为:
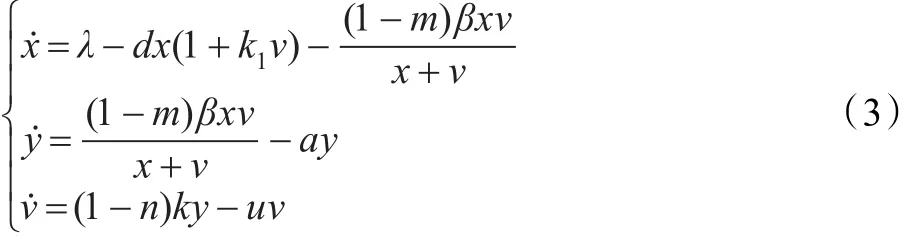
其中变量x,y,v和参数λ,d,β,a,k,u,k1的含义与模型式(2)相同。m,n(0<m,n<100%)表示治疗效果参数。
模型式(3)有两个平衡点:

是病毒清除平衡点,表示患者体内HIV被清除。其中x0=λ/d。

是持续带毒平衡点,表示患者体内HIV持续感染。其中:

其中:

是模型式(3)的基本再生数,且与人体内CD4+T细胞总数无关。
3 平衡点稳定性分析
假设模型存在平衡点Q,若存在包含Q的邻域S(δ),当初始值Q0∈S(δ)时,随着时间趋于无穷,模型的解无限趋近于平衡点Q,则平衡点Q为小范围渐近稳定(局部渐近稳定);当初始值Q0∈Rn时,随着时间趋于无穷,模型的解始终无限趋近于平衡点Q,则平衡点Q为大范围渐近稳定(全局渐近稳定)[12]。
常用于判别平衡点局部渐近稳定的方法有特征值正负判别和Routh-Hurwitz判别定理[13-14]。常用于判别平衡点全局渐近稳定的方法有Lyapunov稳定性定理和LaSalle不变集原理[15-17]。
本章首先讨论模型式(3)解的有界性,然后分别论证平衡点Q1和平衡点Q2的稳定性。
3.1 解的有界性
容易证明在初始值为x(0)>0,y(0)>0,v(0)>0的条件下,模型式(3)的解在t>0时全为正。因此,模型式(3)的解存在于非负集合:
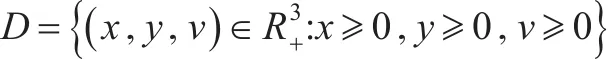
根据模型式(3)前两个等式,可以得到:

则可以得到:

因此x(t),y(t)是有界的。根据模型式(3)第三个等式:

则可以得到:

因此v(t)也是有界的。综上得到D的一个有界子集:
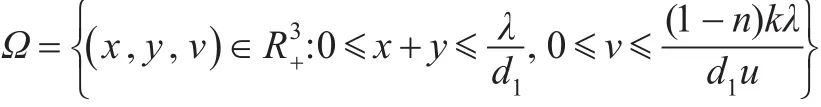
3.2 病毒清除平衡点Q1的稳定性
首先运用特征值正负判别讨论模型式(3)病毒清除平衡点Q1的局部渐近稳定性,然后运用Lyapunov函数和LaSalle不变集原理讨论平衡点Q1的全局渐近稳定性。
定理1若R0<1,则模型式(3)的病毒清除平衡点Q1局部渐近稳定。
证明模型式(3)在平衡点Q1处的Jacobi矩阵为:

其特征方程为:

化简上式为:

求解上式得到:

求解式(8)得到:

因此,若R0<1则有λ2<0和λ3<0,所以模型式(3)的病毒清除平衡点Q1是局部渐近稳定的。
定理2若R0<1,则模型式(3)的病毒清除平衡点Q1在Ω内全局渐近稳定。
证明构造Lyapunov函数:
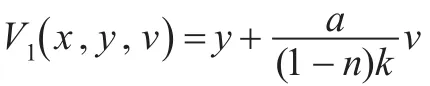
则




构造Lyapunov函数:
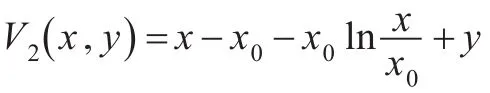
其中,λ=dx0,Q1=(x0,0,0),则

因为λ=dx0,则有:

因为算术平均数大于或等于几何平均数,则有:

可以得到在E1中有≤0 。当且仅当x=x0,y=0时,=0。因此,在E1中存在一个最大不变吸引子集:
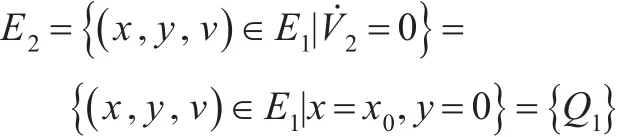
综上所述,若R0<1,则模型式(3)的病毒清除平衡点Q1在Ω内是全局渐近稳定的。
3.3 持续带毒平衡点Q2的稳定性
运用Routh-Hurwitz判别定理讨论模型式(3)持续带毒平衡点Q2的局部渐近稳定性。
定理3若R0>1,则模型式(3)的持续带毒平衡点Q2局部渐近稳定。
证明模型式(3)在平衡点Q2处的Jacobi矩阵为:

其特征方程为:

化简上式为:

记作:
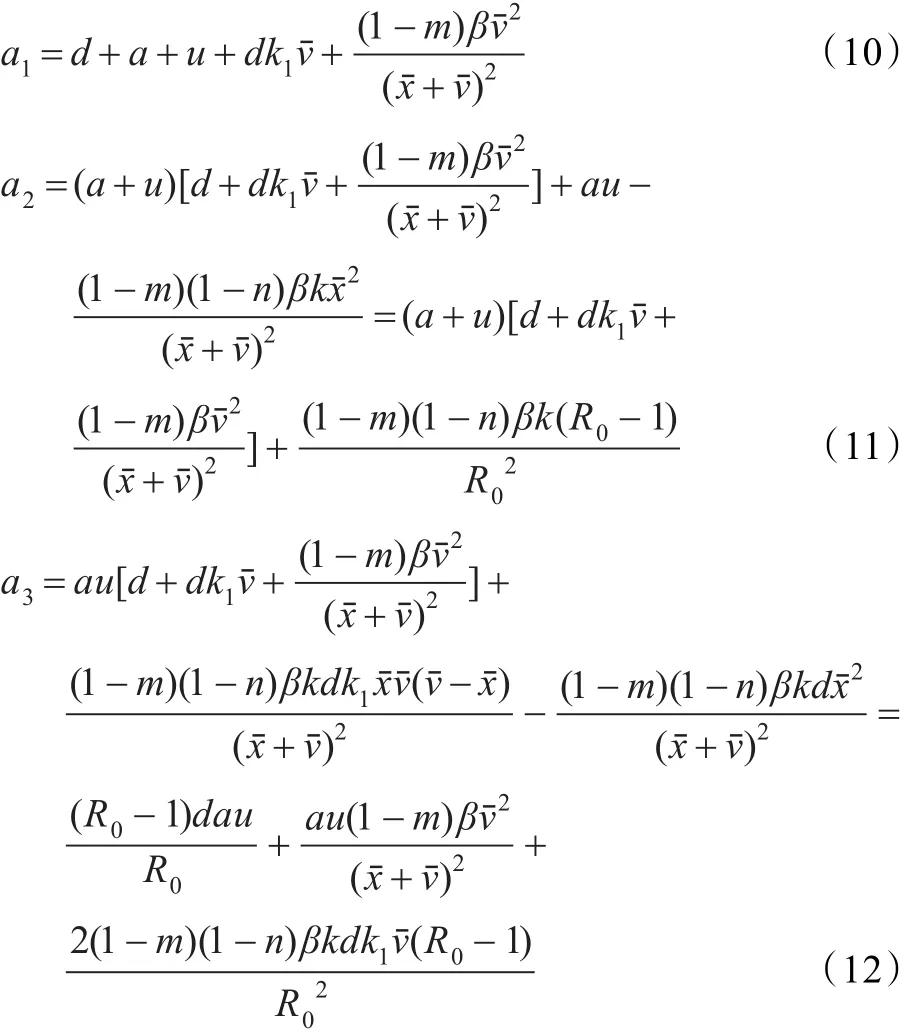
则有:

根据式(10),式(11)和式(12),计算a1a2-a3得到:

当R0>1时,模型式(3)存在平衡点Q2,并且可以得到:a1a2-a3>0 和a3>0,即H2>0,H3>0,则 Routh-Hurwitz判别定理得以满足。因此,若R0>1模型式(3)的持续带毒平衡点Q2局部渐近稳定。
4 抗HIV感染治疗数值模拟
基于斯坦福大学HIV耐药性数据库的临床数据和计算机模拟平台Matlab,运用模型式(3)模拟一组患者抗HIV感染治疗动力学。
4.1 抗HIV感染药物组合治疗
Baxter等报道了一项HIV耐药性的随机性研究,该研究中所有患者均接受了抗HIV感染药物组合治疗,且药物的组合由蛋白酶抑制剂和逆转录酶抑制剂构成[18-19]。所有患者均在第0、4、8、12周进行了血液检测,每次检测都包括血液中CD4+T细胞计数和HIV RNA载量[18-19]。
根据使用药物的不同,从Baxter研究中选出一组患者。该组共15名患者,服用的蛋白酶抑制剂为利托那韦(RTV)和沙奎那韦(SQV),逆转录酶抑制剂为司坦夫定(D4T)。运用模型式(3)对该组患者抗HIV感染治疗进行数值模拟,并对该组患者抗HIV感染治疗疗效做长期预测。
4.2 RTV+SQV+D4T组合治疗模拟
首先确定模型式(3)参数取值或取值范围:
(1)正常CD4+T细胞凋亡的半衰期为50 d[20],可以得到d=-ln(0.5)/50≈0.013 9。
(2)因为健康人体内平均含有830/μl CD4+T细胞[21],则有λ=d×830≈0.013 9×830=11.537 0。
(3)因为具有复制病毒能力的已感染CD4+T细胞存活时间短,其半衰期大约为1.2 d[22],则有a=-ln(0.5)/1.2≈0.577 6。
(4)因为 HIV 在血液中的半衰期为 1~2 d[22],则有u=-ln(0.5)/1.5≈0.462 1。
(5)根据文献[23],得到其他参数的取值范围:β∈[2.5 × 10-4,0.5],k∈[2,1 250],m∈[0,1],n∈[0,1]。
运用患者的临床数据,确定了以下参数取值:β=6×10-2,k=34 ;参数k1,m,n和基本再生数R0不同时间的变化取值见表1。

表1 不同时间的k1,m,n和 R0取值
运用模型式(3)对RTV+SQV+D4T组合治疗进行模拟,数值模拟结果见图1和2。
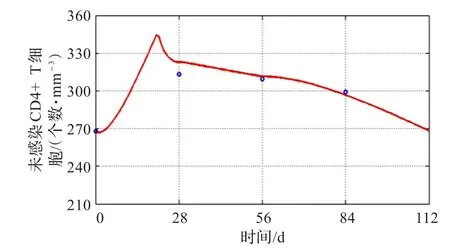
图1 抗HIV感染治疗模拟CD4+T细胞计数变化

图2 抗HIV感染治疗模拟HIV RNA载量变化
通过图1和2,可以得到治疗前3周的抗HIV感染治疗使得患者的基本再生数R0从7.643 1降至0.672 6,且HIV对CD4+T细胞凋亡诱导作用较小。因此,患者的平均HIV RNA载量快速下降,平均CD4+T细胞计数快速回升,并逼近病毒清除平衡状态。
第3周之后,HIV对CD4+T细胞凋亡诱导作用加剧,导致患者平均CD4+T细胞计数开始下降,但抗HIV感染治疗没有恶化,患者的R0保持不变,平均HIV RNA载量没有反弹。然而,HIV耐药性在第4周后出现,使得药物疗效参数n从0.84降至0.759,该组患者的R0从0.672 6升至1.013 1。因此,患者平均HIV RNA载量缓慢反弹,平均CD4+T细胞计数持续下降,并逼近新的持续带毒平衡状态。
第8周之后,HIV耐药性增强,使得药物疗效参数m从0.45降至0.449,n从0.759降至0.755。该组患者的R0从1.013 1升至1.031 8。由于药物抑制HIV感染作用减弱,更多HIV参与感染CD4+T细胞,所以HIV对CD4+T细胞凋亡诱导作用轻微减弱,但仍强于初始水平。因此,患者平均HIV RNA载量继续缓慢反弹,平均CD4+T细胞计数继续下降,并逼近新的持续带毒平衡状态。
4.3 RTV+SQV+D4T组合治疗长期预测
根据2013年世界卫生组织出版的HIV治疗指南[24],病毒载量作为首选标准,用以监测、诊断和确定抗逆转录病毒治疗失败;治疗失败定义为在至少6个月的药物治疗后,持续出现病毒载量超过1 000 copies/mL。然而,Baxter研究中所有患者的HIV RNA载量仅仅在第0、4、8、12周进行检测[18-19]。因此,有必要做长期预测以确定RTV+SQV+D4T组合治疗是否失败。
假设:在第12周检测之后,该组患者继续保持2年的抗HIV感染治疗,在这两年中,HIV耐药性没有恶化,药物疗效没有变化,所有参数取值保持不变。运用模型式(3)对该组患者抗HIV感染治疗进行长期预测模拟。
RTV+SQV+D4T组合治疗长期预测模拟结果见图3和4。

图3 长期预测CD4+T细胞计数变化

图4 长期预测HIV RNA载量变化
观察到在第12周检测之后,该组患者平均CD4+T细胞计数持续下降最终保持在一个低于基线值的水平;平均HIV RNA载量持续上升,但没有超过基线值。并且,该组患者的平均HIV RNA载量始终大于1 000 copies/mL。长期预测说明该组患者的抗HIV感染治疗是失败的,应该及时换用更为有效的抗HIV感染治疗方法。
5 结论
提出一个改进的含有饱和发生率和HIV诱导CD4+T细胞凋亡机制的抗HIV感染治疗模型,来描述抗HIV感染治疗动力学。模型的基本再生数R0与CD4+T细胞总数无关,而且凋亡率同时包含CD4+T细胞固有凋亡和有HIV诱导CD4+T细胞凋亡机制,说明改进模型更为合理。改进模型具有两个平衡点Q1和Q2:病毒清除平衡点与持续带毒平衡点。证明了平衡点Q1的局部渐近稳定性和全局渐近稳定性,平衡点Q2的局部渐近稳定性。
基于定理2和定理3,可以得出以下结论:
(1)若HIV感染者自身的基本再生数R0小于1,则其即使感染大量HIV,该感染者仍然能自动痊愈;若某种抗HIV感染药物治疗能使患者的R0小于1,则患者最终能被治愈。
(2)若HIV感染者的基本再生数R0大于1,即使感染微量病毒,感染者将始终处于持续带毒状态;若抗HIV感染药物治疗不能使患者的R0小于1,则患者体内HIV将不能被彻底清除。
基于Matlab平台,运用模型式(3)模拟一组患者抗HIV感染治疗,并对该组患者疗效进行了长期预测。数值模拟说明:抗HIV感染药物可能无法抑制HIV对CD4+T细胞凋亡诱导;HIV耐药性出现后,若不及时更换治疗方案,HIV耐药性可能会增强。长期预测说明该组患者的抗HIV感染治疗是失败的,应及时更换抗HIV感染治疗方案。
文献[25]报道一个HIV感染治愈病例:柏林病人接受两次骨髓移植来更换其体内CD4+T细胞,最终柏林病人得到治愈。结合本文的理论分析(定理2),可以通过假设骨髓移植后新的CD4+T细胞能够抵御HIV感染,即感染率β=0从而R0=0来解释上述病例。综上所述,得出结论:世界上存在一类人群,即使他们感染大量的HIV,也终将不治自愈。
进一步工作:CD8+T细胞是人体中一种重要的免疫细胞,该细胞通过杀伤已感染CD4+T细胞来抑制HIV复制。骨髓移植后,柏林病人体内HIV的彻底清除,可能不仅与移植后CD4+T细胞具有抵御HIV感染能力有关,同时也可能与CD8+T细胞大量杀伤已感染细胞有关。因此,将考虑在本文模型式(3)基础上加入免疫响应功能项,对骨髓移植治愈HIV做更深入分析。
[1]World Health Organization.HIV/AIDS key fact[EB/OL].[2014-07-10].http://www.who.int/mediacentre/factsheets/fs360/en/.
[2]Orellana J M.Optimal drug scheduling for HIV therapy efficiency improvement[J].Biomed Signal Proces,2011,6:379-386.
[3]Wang Y,Zhou Y.Mathematical modeling and dynamics of HIV progression and treatment[J].Chin J Eng Math,2010,27(3):534-548.
[4]Nowak M A,Bangham C R M.Population dynamics of immune response to persistent viruses[J].Science,1996,272(5258):74-79.
[5]Nowak M A,Bonhoeffer S,Shaw G M,et al.Anti-viral drug treatment:dynamics of resistance in free virus and infected cell populations[J].J Theor Biol,1997,184:203-217.
[6]Nowak M A,May R M.Virus dynamics[M].Oxford:Oxford University Press,2000.
[7]Leenbeer P D,Smith H L.Virus dynamics:a global analysis[J].SIAM J Appl Math,2003,63(4):1313-1327.
[8]季语,闵乐泉,苏永美,等.具有饱和发生率的病毒感染模型的全局稳定性分析[J].生物数学学报,2010,25(2):267-272.
[9]Holm G,Gabuzda D.Distinct mechanisms of CD4+and CD8+T-Cell activation and bystander apoptosis induced by human immunodeficiency[J].J Virol,2005,79(10):6299-6311.
[10]Yue F Y,Kovacs C M,Dimayuga R C,et al.Preferential apoptosis of HIV-1-specific CD4+T cells[J].J Immunol,2005,174:2196-2204.
[11]孙立哲,马文丽,孙汉顺,等.HIV感染动力学模型概述[J].生物信息学,2012,8(4):302-306.
[12]郑大钟.线性系统理论[M].北京:清华大学出版社,2002.
[13]Kuang Y.Delay differential equations with applications in population dynamics[M].London:Academic Press,2004.
[14]Srivastava P K,Chandra P.Modeling the dynamics of HIV and CD4+T cells during primary infection[J].Nonlinear Anal-real,2010,11(2):612-618.
[15]LaSalle J P.The stability of dynamical systems[M].Philadelphia:Society for Industrial&Applied Mathematics,1976.
[16]肖燕妮,周义仓,唐三一.生物数学原理[M].西安:西安交通大学出版社,2012.
[17]Buonomo B,Vargas-De-Le´on C.Global stability for an HIV-1 infection model including an eclipse stage of infected cells[J].J Math Anal Appl,2012,385:709-720.
[18]Baxter J D,Mayers L D,Wentworthet N,et al.A randomized study of antiretroviral management based on plasma genotypic antiretroviralresistance testing in patients failing therapy[J].AIDS,2000,14(9):83-93.
[19]Stanford University.Clinical trial datasets GART study[EB/OL].[2014-07-10].http://hivdb.stanford.edu/pages/clinicalStudy-Data/GART.html.
[20]Bourgeois C,Hao Z,Rajewsky K,et al.Ablation of thymic export causes accelerated decay of naive CD4+T cells in the periphery because of activation by environmentalantigen[C]//ProcoftheNational Academy of Sciences of the United States of America,2008,105(25):8691-8696.
[21]Bofill M,Janossy G,Lee C A,et al.Laboratory control values for CD4 and CD8 T lymphocytes.Implications for HIV-1diagnosis[J].Clin Exp Immunol,1992,88(2):243-252.
[22]Kuritzkes D R.HIV pathogenesis and viral markers[EB/OL].(2000-04-07).http://www.medscape.org/viewarticle/421048.
[23]Wang Y,Zhou Y,Wu J,et al.Oscillatory viral dynamics in a delayed HIV pathogenesis model[J].Math Biosci,2009,219(2):104-112.
[24]World Health Organization.Consolidated guidelines on general HIV care and the use of antiretroviral drugs for treating and preventing HIV infection:recommendations for apublichealthapproach[M].Geneva:WHO Press,2013.
[25]Hutter G,Nowak D,Mossner M,et al.Long-term control of HIV by CCR5 Delta32/Delta32 stem-cell transplantation[J].N Engl J Med,2009,360:692-698.

