简论数学情境教学的认识论基础

李 三 平，朱　瑶

(陕西师范大学 数学与信息科学学院，陕西 西安 710119)

简论数学情境教学的认识论基础

李 三 平，朱瑶

(陕西师范大学 数学与信息科学学院，陕西 西安 710119)

摘要：数学情境教学具有其相对独立的特点，主要为“以境启知、以知怡情”。从教学认识论角度看，生活认识论及建构主义认识论可以作为数学情境教学的认识论基础；从数学认识论角度看，可误主义或拟经验主义数学认识论可以作为数学情境教学的认识论基础。

关键词：情境教学；数学情境教学；教学认识论；数学认识论

一、研究背景

自20世纪70年代以来，“情境教学”在我国基础教育的各个学科中已经有许多相关理论探讨及实践研究，并且主要集中在语文、外语及思想品德等文科课程的教学中。到了21世纪，随着基础教育课程改革的逐步推进，越来越多的数学教育工作者开始关注情境教学。另外，《义务教育教学课程标准(2011)》中指出，“数学教学应根据具体的教学内容，注意使学生在获得间接经验的同时也能够有机会获得直接经验，即从学生实际出发，创设有助于学生自主学习的问题情境，引导学生通过实践、思考、探索、交流等，获得数学的基础知识、基本技能、基本思想、基本活动经验，促使学生主动地、富有个性地学习，不断提高发现问题和提出问题的能力、分析问题和解决问题的能力”，[1]也正因为如此，许多教师认为，情境教学恰好符合新课程标准的要求，较好地实现了数学教学与学生生活经验的沟通，这也就促使了具有相对独立特点的数学情境教学研究也获得了较大发展。

我们从中国知网对“数学情境教学”的相关期刊论文进行了检索与统计，结果见表1。

表1　知网“数学情境教学”相关文献检索统计表(2000-2015.1)

注：A：中国学术期刊，B：特色期刊，C：博士学位论文，D：硕士学位论文，E：中国重要会议， F：中国重要报纸

从表1统计情况可知，自21世纪以来，有关“情境教学”、“数学情境教学”的研究已经得到了数学教育界的普遍重视。对“情境教学”的研究明显多于对“数学情境教学”的研究，而且有关“数学情境教学”的研究，主要集中在一些期刊论文中，并以案例叙述加经验总结的讨论方式为主。虽然硕士学位论文中已有相当一部分的研究，但是博士学位论文对此问题的研究还很少见。从已有研究内容看，数学情境教学的相关研究主要集中于情境教学理论在中小学数学教学中的应用研究，具体数学知识内容的情境教学设计研究，新旧教材中情境设置的比较研究，以及情境与提出问题教学模式对比研究等，而对于数学情境教学的理论研究却相对较少。

本文将从认识论的视角出发，对数学情境教学进行探讨，以期为数学情境教学的理论梳理和进一步研究提供微薄之力。

二、“数学情境教学”概念的认识

数学情境教学的定义尽管至今尚未统一，但是较一致的看法是，数学情境教学的本质包括“情”与“境”两个方面。[2]数学教学与语文、思想政治、历史等文史学科教学不同的地方可能在于，数学教学较难找到那种能激起学生真实的、强烈的情感反应而又与数学教学内容非常贴切的情境。

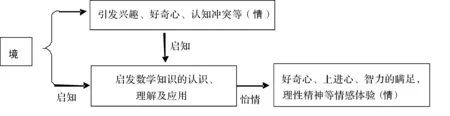
图1　数学情境教学主要特点

由于数学学科的独特性，从某种意义上说，数学教学是“知情教学”[3]，是以知生情的教学。我们认为，数学情境教学的主要特点为“以境启知，以知怡情”(如图1)。忽视“知”则会导致数学情境教学缺乏数学味，忽视“境”与“情”则不能称其为情境教学。这里“境”的作用更多的在于启“知”(即情境的问题化与问题的知识化)，而“知”的形成必然包括一个“去情境化、去个人化和去时间化”[3]的过程，那种以矫揉造作的方式营造的情境氛围一方面不利于学生对数学知识的获得，另一方面也难以激起学生真实的情感。然而，据我们调查和了解，在具体的教学实践中，教师们中出现过一些片面化及绝对化的认识，有些人认为，数学情境教学，即是指创设生活情境，数学情境教学即指用直观的教具代替传统的言语传递，在教学过程中只重情境创设过程忽视去情境过程，以致数学情境教学有情境但却没有了数学，这当然不是数学情境教学的初衷。出现这些认识上的误区，其主要原因可能还在于那种唯一强调变革力量，并主要依靠行政力量与“由上至下”的模式进行运作的课程改革方式[5]。还有作者指出，在情境教学被广泛接受并大量使用于教学中的同时，也存在着一些使用上的误区。[5]事实上，数学情境教学有三个环节，第一个环节：情境化(创设数学教学情境)；第二个环节：去情境化(提出数学问题，解决数学问题)；第三个环节：再情境化(注重数学知识应用)。也就是说，创设教学情境仅是情境教学的一个开始环节，并不是情境教学的全部，其作用主要在于激发学生的学习动机，沟通学生的生活实际与数学知识内容之间的联系，搭建具体形象与概括抽象的桥梁，为后续的“去情境化”等教学环节做好准备。也正由于“学校数学”的任务，就是要使学生获得严谨、抽象、概括等一般化知识和思维方法，并能应用于实际问题中，因此，设置了情境的“生活数学”只有实现对于具体情境的“超越”，即“去情境化”，才能促使学生自觉地建构起数学知识的意义，进而完成“学校数学”教学的任务。

三、数学情境教学的认识论探讨

认识论作为哲学的一个组成部分，专门探讨人类认识的本质、结构，认识与客观实在的关系，认识的前提和基础，认识发生、发展的过程及其规律，以及认识的真理标准等等问题。作为学科教学的数学教学具有“二重性”，即“教与学，教与数学”对应的数学教学二重原理,数学教育是学科教育，如果数学教育不是把“教与数学对应起来”，就不能称其为数学教育。[6]对数学情境教学的认识论基础探讨，则也离不开对教学认识论及数学认识论的探讨。

1.数学情境教学的教学认识论基础

“生活认识论”和“建构主义认识论”可以作为数学情境教学的教学认识论基础。

很长一段时间以来，受工具性认识论的影响，数学教学被视为使受教育者获得数学知识，发展数学能力以及为未来生活做准备、打基础的教学，教师为了帮助学生掌握知识而教，学生为获得知识、为将来生活奠定基础而学，将课堂教学视为纯粹的认知活动和理性活动，这样的教学罔顾学生的实际生活，难免冷漠无情。作为工具性认识论的变革与超越，生活认识论强调为学生的当下生活而教，将认识作为人生活的一种方式，当作认识者的自我生成，自我实现，自我完善的方式，[7]而不是为了获得关于对象的客观知识的工具。情境教学的核心是“情境”，它将淡化了的情感、意志、态度等心理要素确定为学科教学的有机构成，通过各种生动、具体的生活情境的创设拉近了教学与学生现实生活的距离，使死的知识成为活的生活。[8]

教学认识主要属于个体认识中对间接经验的认识，即对人类已知事物的再认识。建构主义认识论认为，对间接经验的认识一般遵循“同化——顺应”的规律，强调学习过程是学习者原有认知结构与环境中接受的感觉信息相互作用，主动建构信息意义的生成过程。个体的认识不是对对象的被动反映而是主动建构联系，将学生的直观经验与新知识建立联系，则必须使新知识的学习具有丰富的情境性。需要强调的是，这里的情境对学生来说应具有心理表征的直观性及知识运用的真实性，而不是指“直接可见与真实发生”。

博文(Brown)等人认为：“知识决不能从它本身的环境中孤立出来，学习知识的最好方法就是在情境中进行。”[9]在教育界中有这样一种质疑，即在很多时候我们可以不运用情境，比如，我们可以根据数学知识的内部逻辑结构通过直接讲授也能让学生学会知识，并且很多一线教师也在按照这种被认为是最经济最高效的讲授方式授课。这样的质疑一方面表现了质疑者并没有正确认识教学的实质，将教学仅仅视为客观知识的习得；另一方面也表现了质疑者是站在教学内部以及知识的内部来认识知识。这种去情境化的教学，虽然也能使学生习得知识，但是这种知识是“惰性知识”[10]，学生难以在现实问题情境中提取及运用所学知识，更难以运用所学知识来解决实际中面临的问题。

2.数学情境教学的数学认识论基础

离开了关于知识的观点，就不可能有关于学习的观点，离开了关于学习的观点更不可能有关于教学的观点，对数学本身的认识制约着关于数学教学的认识。数学认识论主要关注现实世界的空间形式和数量关系与数学结构的关系等问题。从研究对象来看，数学研究的是经过抽象了的思维的产物，例如，数，理想化的点、线、面等，这些对象在早期的数学研究中大多能找到现实原型；虽然随着数学理论自身逻辑发展的需要，数学的现代研究，如群论、非欧几何等，难以在当时找到现实原型，但后来发现大量的数学知识在物理、计算机、天文学等领域中找到了应用。而中小学阶段所学习的大部分初等数学知识更是具有最初的现实原型，这就为情境教学的实施提供了“物质”保证。

目前，数学认识论在基本观念方面发生了革命性的变化，由“绝对主义”的数学观转变为“可误主义”或“拟经验主义”的数学观。[11]数学“拟经验主义”作为对数学“绝对主义”的否定，将数学看作是动态的、可误的、是与人类整体知识结构相联系的，是人类文化的重要组成部分，并且注重数学知识的发生过程，把数学看作是历史及人类实践的组成部分，强调数学认识中的“发现”。对数学教育的启示主要有，数学既被当作一种知识的特定体系，是学校教学可教的内容；又被看成一种特定称之为数学化的活动，包括模式识别、一般化以及证明等。[11]就将数学视为历史及人类实践的组成部分的认识而言，它沟通了数学与其他学科及人类环境条件的联系，而数学情境教学的认识论意义也正在于沟通了直接经验与间接经验以及“知情”和学科之间联系的断层问题。[12]将数学视为数学化的活动，表现在数学教学中即强调数学的实践，由于数学较其他学科更为抽象和概括，不仅就研究对象而言，而且其语言也是高度形式化了的抽象语言，若不经过具体到抽象的数学化概括过程，则易使学生造成表面形式的理解，即只掌握了数学对象的形式而难以掌握形式背后的实质。数学情境教学在创设情境及情境的数学化处理过程中蕴含了将实际问题数学化处理的过程，体现了数学知识是怎样被包含在现实生活中又是如何被发现的过程。

四、结语

数学情境教学在实施过程中出现的主要矛盾为情境化与数学化的矛盾。极端的表现为两种片面，一是片面强调现实生活，二是片面强调数学内部逻辑，然而教育本身即是在矛盾中寻求平衡。从教学认识论及数学认识论的发展也可以发现，新的认识论总是在已有认识论所表现的局限性中突破创新，注重学生当前的现实生活，在现实情境中进行数学知识的学习，以及注重数学知识与其他学科知识及人类环境的联系，都将表明进行数学情境教学的必要性。

基于教学认识论及数学认识论的讨论，足见数学教学不能不回归学生的现实生活，但也不可能完全回归生活，数学教学不能不注重数学知识的积累但也应注重数学的现实应用。教育是一个“慢”的过程和活动，很多时候功利性的模仿，或许会较迅速的改变现状，但这样的简单模仿只会带来混乱和传统优势的丢失。对情境教学模式的研究与推行，还需要研究者及一线教师从其教学理论，以及产生此教学理论的元理论(认识论)出发，进一步认真深入地思考。

[参考文献]

[1] 教育部.义务教育数学课程标准[M].北京：北京师范大学出版社,2012:42.

[2] 栾庆芳，朱家生.数学情境教学研究综述[J].数学教学通讯，2006(3):1-4.

[3] 郑毓信.数学的文化价值何在、何为——语文课反照下的数学教学[J].人民教育， 2007(6):38-41.

[4] 郑毓信.课改背景下的数学教育研究[M].上海：上海教育出版社，2012:109.

[5] 潘胜洪.数学情境教学中的去情境化问题初探[J].扬州教育学院学报,2008(3)：72-75.

[6] 涂荣豹.论数学教育研究的规范性[J].数学教育学报，2003(11)：2-5.

[7] 王攀峰.现代教学论的发展趋向：生活认识论的启示[J].首都师范大学学报:社会科学版，2007(6):122-130.

[8] 李吉林.为全面提高儿童素质探讨一条有效途径——从情境教学到情境教育的探讨与思考[J].教育研究，1997(3):33-41.

[9] BROWN,J.S,COLLINS,A,DUGUID,P.Situated cognition and the culture Of learning[J].Educational Researcher,1989,18(1):32-41.

[10] [英]怀特海.教育的目的[M].庄莲平，王立平,译.上海：文汇出版社，2012:2.

[11] 綦春霞.数学认识论的历史及其发展趋势[J].数学教育学报，2002(2):28-31.

[12] 郝京华.情境教学三部曲的认识论意义[J].课程·教材·教法，2009(6):27-30.

Epistemological Foundations of Mathematics Situational Teaching

LI San-ping, ZHU Yao

(SchoolofMathematicsandInformationScience,ShaanxiNormalUniversity,Xi’an710119,Shaanxi)

Abstract:Situation teaching of mathematics has relatively independent features. The main feature is “to enlighten with context, and to cheer with knowledge”. From the perspective of teaching epistemology, living epistemology and constructivist epistemology can be used as the epistemological foundations situational teaching of mathematics; from the perspective of mathematic epistemology, semi-experience epistemology of mathematics may be used as the epistemological foundations of mathematics situational teaching.

Key words:situational teaching; situational teaching of mathematics; epistemology

作者简介：李三平，男，陕西周至人，陕西师范大学数学与信息科学学院副教授；朱瑶，女，四川南充人，陕西师范大学数学与信息科学学院硕士研究生。

基金项目：陕西师范大学研究生教育教学改革研究项目(GERP-14-11);陕西师范大学教育教学改革研究项目(1107080075)

收稿日期：2015-09-29

中图分类号：G652

文献标识码：A

文章编号：1674-2087(2015)04-0072-04