瓦楞纸板的压缩变形及吸能特性研究

付云岗 郭彦峰 王忠民

(1.西安理工大学机械与精密仪器工程学院,陕西西安,710048；2.西安理工大学印刷包装工程学院,陕西西安，710048；3.西安理工大学土木建筑工程学院,陕西西安，710048)



瓦楞纸板的压缩变形及吸能特性研究

付云岗1,2郭彦峰2王忠民3

(1.西安理工大学机械与精密仪器工程学院,陕西西安,710048；2.西安理工大学印刷包装工程学院,陕西西安，710048；3.西安理工大学土木建筑工程学院,陕西西安，710048)

以瓦楞楞型不同的B型和C型瓦楞纸板为研究对象,在7种压缩速率下进行了准静态压缩实验,分析了瓦楞纸板的变形模式和静态性能,得到了瓦楞纸板横向压缩力学性能和能量吸收性能,并绘制了不同压缩速率下瓦楞纸板的能量吸收图、能量吸收效率曲线及质量比吸能曲线。实验结果表明,低压缩速率对瓦楞纸板的最佳能量吸收点、能量吸收效率、质量比吸能等性能基本无影响；而截面几何尺寸对瓦楞纸板的能量吸收性能影响较大,在相同压缩速率下,B型瓦楞纸板的单位体积吸收能、结构变形利用率、质量比吸能均优于C型瓦楞纸板。

瓦楞纸板；压缩变形；吸能特性；能量吸收图

夹层结构因具有优良的比强度、比刚度等特性,而被广泛应用于航空、航天、海洋及民用等冲击防护领域。瓦楞纸板作为典型的夹层结构,具有较高的比能量吸收(单位质量的能量吸收),被普遍应用于各类产品的缓冲吸能单元,通过自身的结构变形来耗散施加于包装件上的能量以确保产品安全。随着人们减少材料用量、节能降耗、可持续发展等环保意识日益增强,瓦楞纸板作为绿色缓冲材料在物流运输包装领域越来越受关注。

夹层结构在横向压缩载荷作用下的力学特性是影响夹层板结构在冲击载荷下动态性能的关键因素之一。国内外众多学者对各类夹层结构的横向压缩力学性能、变形机制和能量吸收展开了深入研究。Yan等人[1]通过对比实验研究了金属三角型夹层板与闭孔泡沫铝充填的金属三角型夹层板的变形模式及吸能特性,并与数值模拟的结果保持一致。Zhang等人[2]通过三点弯曲实验和静态压缩实验研究了梯型夹层结构的比刚度、比强度和失效模式,探讨了夹层倾角、芯层厚度、黏合长度及面板纤维类型等因素对夹层结构吸能特性的影响。Vijayasimha Reddy等人[3]研究了丝棉木-铝蜂窝多孔夹层结构在准静态及低速冲击载荷下的冲击响应和吸能特性,分析了冲击速度和夹层类型对能量吸收的影响。张延昌等人[4]基于准静态压缩实验与数值仿真研究了金属V型夹层结构的变形模式与吸能效率,并提出夹层的变形模式决定了夹层结构的横向压缩力学行为及其能量吸收。Wang[5]基于动态缓冲实验研究了蜂窝纸板缓冲吸能性的影响因素,以利于蜂窝纸板结构的优化设计和包装材料的选择。

对于瓦楞夹层结构,国内外学者的研究主要集中在静态力学性能、动态缓冲性能、失效准则的理论和实验研究。Nordstrand等人[6]通过瓦楞夹层结构的剪切刚度研究了不同芯层形状对横向剪切模量的影响,并基于刚性面板提出了瓦楞芯层横向剪切模量的最大值。Winkler等人[7]探讨了瓦楞夹层结构的截面几何尺寸对等效薄板模型的刚度及各向异性的影响。王冬梅等人[8]研究了中等应变率下不同楞型的多层瓦楞纸板的力学性能,结果表明，不同的变形机制使得动态平台应力值比静态平台应力值明显增加。Ulf Nyman等人[9]基于材料失效和结构局部屈曲失效,建立了瓦楞纸板面板失效应力准则。这些研究都为瓦楞纸板的防护设计提供了指导和依据。

作为包装容器或缓冲包装材料,瓦楞纸板通过吸收和消耗冲击能量,有效利用材料或结构的变形,使传递到产品上的最大作用力低于其损伤阈值[10]。能量吸收性能已成为瓦楞纸箱、瓦楞缓冲结构的重要设计依据和评价准则。本研究以典型瓦楞纸板为例,基于不同压缩速率的准静态压缩实验,分析了瓦楞纸板的变形模式,研究了瓦楞纸板横向压缩力学性能,通过能量吸收图、能量吸收效率曲线及质量比吸能曲线表征了能量吸收性能,为瓦楞纸板吸能单元的轻量化设计提供参考依据。

1 实 验

1.1 材料

实验用瓦楞纸板为西安秉信纸业有限公司生产的楞型分别为B型和C型的单瓦楞纸板,试样的几何尺寸、材料参数如图1和表1所示。按照GB/T 8168—2008标准制作试样,试样尺寸为100 mm×100 mm,并按GB/T 4857.2—2005的规定对试样在温度23℃、相对湿度60%的环境下处理48 h以上。

图1 瓦楞纸板的几何尺寸示意图

楞型定量/g·m-2面纸芯纸试样质量/g截面几何尺寸/mmtftcH2λB1451506.050.2620.2603.006.02C1451507.560.2620.2603.988.12

1.2 实验过程

采用HT-2402电脑伺服控制材料实验机来研究B型和C型瓦楞纸板的横向压缩特性,实验原理及仪器如图2所示。实验中采用恒定速率方式对试样进行加载,分别对B型和C型瓦楞纸板设定1、6、12、18、24、32和48 mm/min 7种压缩速率进行横向压缩测试。横向载荷、芯层位移通过材料实验机自动记录,芯层变形失效过程由数码摄像机记录。

图2 实验原理及仪器图

2 结果与讨论

通过静态压缩实验得到了横向压缩应力-应变曲线、芯层截面的变形图,从而分析了瓦楞纸板芯层结构的变形模式及压缩渐进屈曲过程,并根据载荷-位移曲线分析瓦楞纸板的横向承载能力及能量吸收性能。

2.1 变形模式

瓦楞纸板芯层截面压缩变形过程如图3所示。图3反映了瓦楞纸板芯层的压缩渐进屈曲模式,2种楞型的瓦楞纸板芯层变形过程基本一致。根据材料实验机记录的横向载荷和芯层位移,可得到瓦楞纸板的横向压缩应力-应变曲线(见图4)。瓦楞纸板在横向压缩载荷作用下经历了弹性变形阶段、初始屈服阶段、渐进屈曲阶段、失稳密实阶段,表现出持续压溃现象,具有较长的平台阶段,从而可吸收较大的能量。具体变形模式及性能分析如下。

图3 瓦楞纸板芯层横向压缩变形图

图4 不同压缩速率下单瓦楞纸板的应力-应变曲线

(1)弹性变形阶段 瓦楞纸板芯层开始变形,且瓦楞胞元两侧变形对称,如图3(Ⅰ)所示。这一阶段主要表现为应力和应变呈双曲正切型关系,且变形较小。

(2)初始屈服阶段 随着变形的增大,瓦楞纸板芯层波峰、波谷逐渐变得扁平,芯层与上、下面纸的接触面积开始增大,如图3(Ⅱ)所示。这一阶段主要表现为在承载应力达到峰值前后出现一定的峰宽,而且B型瓦楞纸板的应力峰值高于C型瓦楞纸板、B型瓦楞纸板的应力峰宽小于C型瓦楞纸板,表明B型瓦楞纸板的抗压强度较高、抗压稳定性较差。

(3)渐进屈曲阶段 随着横向载荷的逐渐增大,面纸与芯层的接触部位形成局部塑性屈曲,受材料非线性、结构不对称等因素的影响,瓦楞纸板芯层两侧塑性屈曲部位的坍塌速度并不相同,瓦楞纸板芯层开始向一侧倾斜,如图3(Ⅲ)所示。这一阶段应力-应变曲线的平台区总体趋势向下,表明瓦楞纸板稳定性下降,承载能力也逐渐下降。

(4)失稳密实阶段 当瓦楞纸板芯层两侧的塌陷部位使瓦楞纸板芯层一侧变得近似竖直时,该侧的芯层壁突然失稳,瓦楞纸板整体开始出现密实化现象,面纸与芯纸接触部分逐渐增加,直至压溃,如图3(Ⅳ和Ⅴ)所示。这一阶段应力随着应变的增大快速增大,失去能量吸收能力。

2.2 能量吸收图

瓦楞纸板的应力-应变(σ-ε)曲线与应变轴之间所包含的面积就是其吸收能量(W),即

(1)

式中,σ(ε)为瓦楞纸板的应力,ε为瓦楞纸板受压时的应变。

能量吸收图由Maitisk[11]和Gibson等人[12]提出,表征缓冲吸能材料或结构基材所承受的应力和吸收的能量之间的关系(其横、纵坐标通常采用缓冲吸能材料或结构基材的弹性模量(Es)进行标准化，见图5),能量吸收曲线上通常会出现一个肩点,该点即为缓冲吸能材料或结构基材在某一应变下的最佳能量吸收点(最佳吸能设计点)。单瓦楞纸板在不同压缩速率下的能量吸收曲线如图5所示。从图5可知,不同压缩速率条件下,相同楞型的瓦楞纸板的肩点几乎一致,表明低压缩速率(低应变)对瓦楞纸板的最佳能量吸收点基本无影响。另外,在相同压缩速率条件下,B型瓦楞纸板的肩点均位于C型瓦楞纸板肩点的右上方,表明B型瓦楞纸板单位体积吸收能量的能力较强。

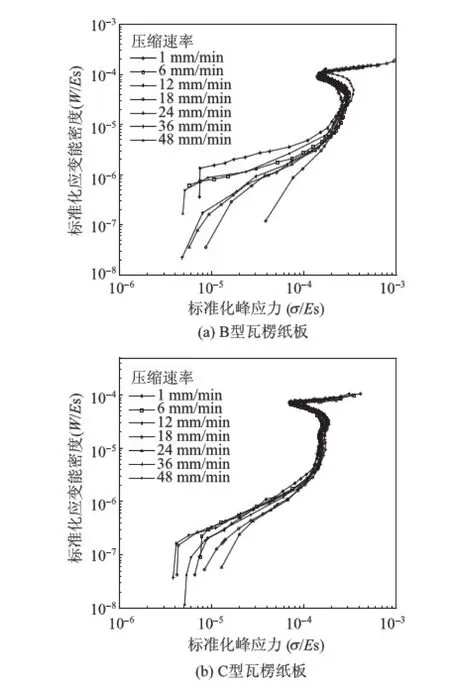
图5 不同压缩速率下单瓦楞纸板的能量吸收曲线

2.3 能量吸收效率

能量吸收效率就是在相同应变时,瓦楞纸板实际吸收的能量与理想弹塑性材料吸收的能量的比值(e)：

(2)

式中,Wi为理想弹塑性材料吸收的能量。用数学软件对σ-ε曲线进行曲线积分,通过式(1)、式(2)可以得到压缩过程中的e-ε曲线。单瓦楞纸板在不同压缩速率下的能量吸收效率曲线如图6所示。从图6可知,①所有试样的能量吸收效率曲线分为典型的“∧”形区域和“∩”形区域2部分。②在“∧”形区域,该阶段初期,瓦楞纸板发生双曲正切型弹性变形,随着变形的增大,能量吸收效率逐渐增大,直至瓦楞纸板开始初始屈服,能量吸收效率迅速下降。③在“∩”形区域的初期,瓦楞纸板胞元上部与下部弯曲部位分别出现了对称屈曲变形,整体承载能力逐渐加强,能量吸收效率快速增大；随着屈曲变形渐进增大,整体承载能力趋于稳定,瓦楞纸板的能量吸收效率在较小的范围内变化,而且峰宽较大,表明瓦楞纸板对渐进屈曲阶段结构变形的利用率较高,能量吸收稳定；当塑性变形继续增大,瓦楞纸板稳定性下降直至失稳,能量吸收效率显著下降。④瓦楞纸板具有较高的能量吸收效率,B型瓦楞纸板的2个峰值的出现均早于C型瓦楞纸板,而且前者“∩”形区域的峰宽大于后者,B型瓦楞纸板的能量吸收稳定性、对结构变形的利用率均优于C型瓦楞纸板。

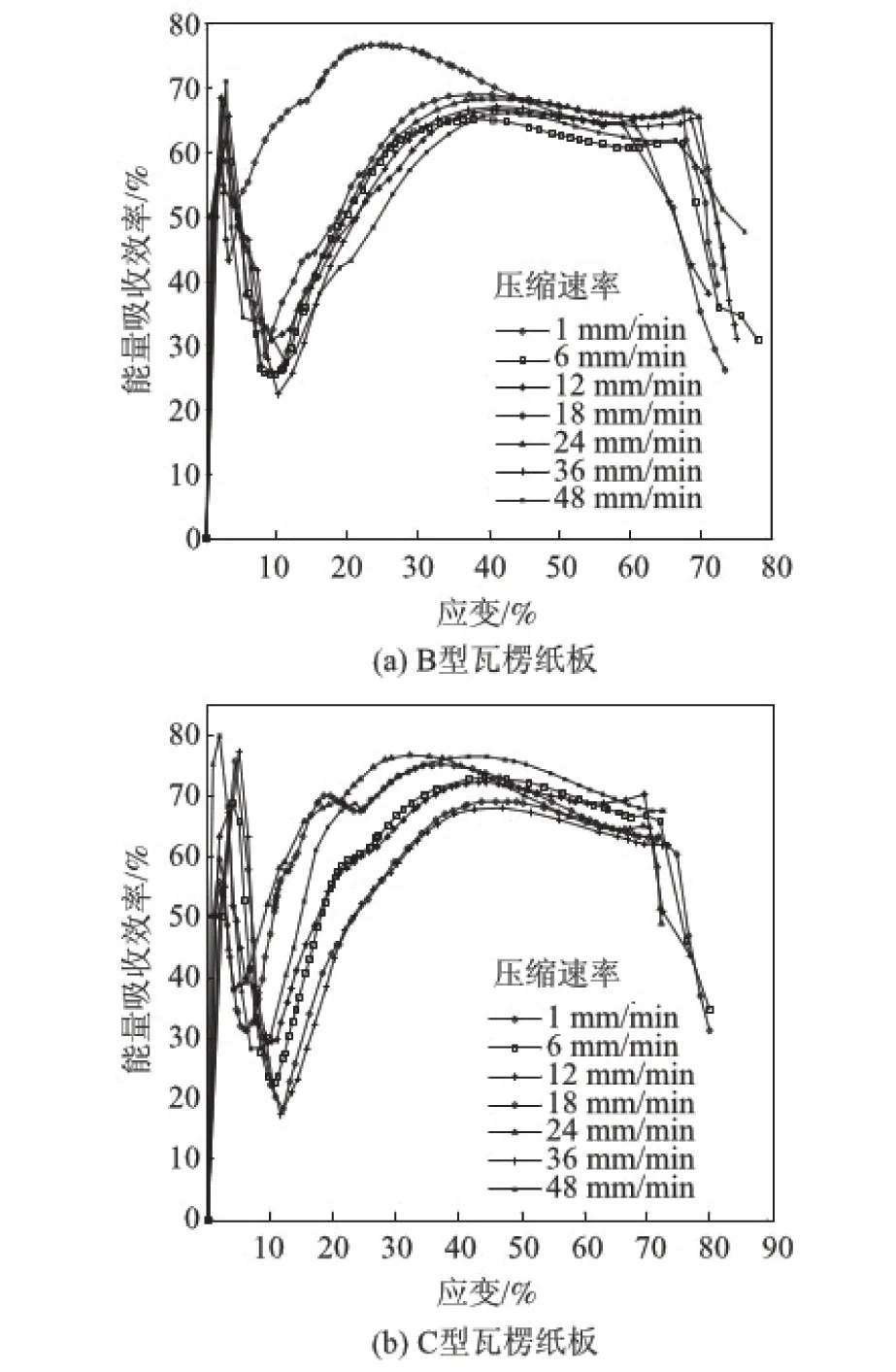
图6 不同压缩速率下单瓦楞纸板的能量吸收效率曲线

2.4 质量比吸能

轻量化设计受到包装行业越来越多的关注和重视,这就要求吸能元件具有较大的质量比吸能。根据准静态压缩过程中所吸收的能量和吸能结构基材的质量,以及准静态压缩的实验结果,可得到在不同压缩速率条件下瓦楞纸板的质量比吸能与应变的关系(见图7)。由图7可知,

(1)随着应变的增大,质量比吸能逐渐增大,但增幅逐渐减小,直至瓦楞夹层结构出现密实化之后,其增幅又迅速变大。

(2)在横向压缩加载初期,质量比吸能受到瓦楞纸板芯层变形模式的影响较大,但随着应变的增大,瓦楞纸板的质量比吸能几乎不受压缩速率的影响。

(3)在相同压缩速率下,B型瓦楞纸板的质量比吸能均大于C型瓦楞纸板,说明截面几何尺寸(惯性矩)对瓦楞纸板的能量吸收性能有一定影响。

图7 不同压缩速率下单瓦楞纸板的质量比吸能-应变曲线

3 结 论

通过7种不同压缩速率的准静态压缩实验,分析了瓦楞纸板在横向压缩载荷下的静态性能及其变形模式,得到了瓦楞纸板的准静态变形模式及其吸能特性。

3.1 瓦楞纸板在横向压缩载荷作用下经历了弹性变形阶段、初始屈服阶段、渐进屈曲阶段、失稳密实阶段,表现出持续压溃现象,具有较长的平台阶段,从而可吸收较多能量。

3.2 通过绘制瓦楞纸板准静态压缩能量吸收图,表征了压缩应力与单位体积吸收能量的变化关系。结果表明,低压缩速率(应变小)对瓦楞纸板的最佳能量吸收点基本无影响。

3.3 瓦楞纸板的能量吸收效率较高,存在2个峰值,渐进屈曲过程中能量吸收效率在较小的范围内变化且峰宽较大,对结构变形的利用率较高,是主要吸能阶段。低压缩速率条件下,随着应变的增大,瓦楞纸板的质量比吸能几乎不受压缩速率的影响。

3.4 通过对瓦楞纸板能量吸收性能的分析可知,截面几何尺寸(惯性矩)对瓦楞纸板的能量吸收性能有显著影响。在相同压缩速率下,B型瓦楞纸板单位体积吸收的能量、结构变形利用率、质量比吸能均优于C型瓦楞纸板。

[1] Yan L L, Yu B, Han B, et al. Compressive strength and energy absorption of sandwich panels with aluminum foam-filled corrugated cores[J]. Composites Science and Technology, 2013, 86: 142.

[2] Zhang J, Peter Supernak, Simon Mueller-Alander, et al. Improving the bending strength and energy absorption of corrugated sandwich composite structure[J]. Materials and Design, 2013, 52: 767.

[3] Vijayasimha Reddy B G, Sharma K V, Yella Reddy T. Deformation and impact energy absorption of cellular sandwich panels[J]. Materials and Design, 2014, 61: 217.

[4] 张延昌, 俞鞠梅, 张世联, 等. V型折叠式夹层板横向压皱吸能特性研究[J]. 振动与冲击, 2014, 33(1): 113.

[5] Wang D M. Impact behavior and energy absorption of paper honeycomb sandwich panels[J]. International Journal of Impact Engineering, 2009, 36(1): 110.

[6] Nordstrand T M, Carlsson L A. Evaluation of transverse shear stiffness of structural core sandwich plates[J]. Composite Structures, 1997, 37: 145.

[7] Winkler M, Kress G. Deformation limits for corrugated cross-ply laminates[J]. Composite Structures, 2010, 92: 1458.

[8] 王冬梅, 柏子游, 龚户祥, 等. 瓦楞夹层结构动态力学性能评估[J]. 振动与冲击, 2014, 33(3): 94.

[9] Ulf Nyman, Per Johan Gustafsson. Material and structural failure criterion of corrugated board facings[J]. Composite Structures, 2000, 50: 79.

[10] 余同希, 卢国兴. 材料与结构的能量吸收[M]. 北京: 化学工业出版社, 2006.

[11] Maitisk, Gibson L J, Ashby. Deformation and Energy Absorption Diagrams for Cellular Solids[J]. Acta Met, 1984, 32(2): 1963.

[12] Gibson L J, Ashby Michanel F. Cellular Solids: Structure and Properties[M]. 2ed. Cambridge: Cambridge University Press, 1997.

(责任编辑：王 岩)

Compression Deformation and Energy Absorption Properties of Corrugated Paperboard

FU Yun-gang1,2,*GUO Yan-feng2WANG Zhong-min3

(1.SchoolofMechanicalandPrecisionInstrumentEngineering,Xi’anUniversityofTechnology,Xi’an,ShaanxiProvince, 710021；2.SchoolofPrintingandPackagingEngineering,Xi’anUniversityofTechnology,Xi’an,ShaanxiProvince, 710021；3.SchoolofCivilEngineeringandArchitecture,Xi’anUniversityofTechnology,Xi’an,ShaanxiProvince, 710021)

(*E-mail： fygpack@xaut.edu.cn)

Taking the B-flute and C-flute corrugated paperboard as research objects, the corrugated paperboards were conducted quasi-static compressive tests under 7 different compressing rates to examine deformation modes and static properties. Transverse compression mechanical characteristics and energy absorption properties were analyzed, energy absorption diagrams, energy absorption efficiency curves and specific energy absorption (SEA) curves were drawn. The results showed that, there was neglected effect of low strain rates on optimum stress of energy absorption, energy absorption efficiency and specific energy absorption of corrugated paperboard, while section geometry of the panel affected the energy absorption properties of corrugated paperboards more obviously. At the same compression rate, energy absorbed per unit volume, structural deformation utilization rate and specific energy absorption of B-flute corrugated paperboard were all greater than that of C-flute panel.

corrugated paperboard； compression deformation； energy absorption property； energy absorption diagram

2015- 01- 06

国家自然科学基金项目(51345008)；教育部留学回国人员科研启动基金项目。

付云岗,男,1981年生；在读博士研究生,讲师；主要从事夹层结构材料的缓冲包装机理及应用的研究。 E-mail：fygpack@xaut.edu.cn

TB332

A

1000- 6842(2015)03- 0031- 05