基于区间平滑的粒子概率假设密度滤波算法

童　骞，李鸿艳，毛少锋，焦　玲，黄明军

(空军工程大学信息与导航学院，陕西 西安　710077)



基于区间平滑的粒子概率假设密度滤波算法

童骞，李鸿艳，毛少锋，焦玲，黄明军

(空军工程大学信息与导航学院，陕西 西安710077)

0引言

2003年，Mahler提出了概率假设密度(Probability Hypothesis Density， PHD)滤波器，该滤波器是一种基于随机有限集(RFS)理论的次最优多目标贝叶斯滤波器[1-2]，它在贝叶斯框架下通过递推形式传递目标的概率假设密度，以实现对目标状态和目标数目的估计，其显著特点是绕过数据关联，有效降低计算量。

当前，PHD滤波的实现主要基于两种方法：一是将概率假设密度的预测和递推都表示为若干高斯分量的和，通过求解高斯分量的权值、均值和协方差阵来估计多个目标的状态和目标数目，即GM-PHDF[3]；二是将一组加权的随机样本逼近概率假设密度分布，利用样本均值运算代替多重积分运算，即P-PHDF[4-6]。前者建立在目标状态的转移密度和似然函数均服从高斯分布的假设条件下，只适用于高斯模型；后者不受系统模型约束，适用于非线性、非高斯情况，运用前景更加可观。然而在P-PHDF算法中，由于使用经典的粒子滤波器实现，仅把系统状态转移概率密度作为重要性密度函数，忽略了观测值的修正作用，使得重要性密度函数严重依赖模型，从而引起从重要性密度函数中采样的样本与真实的后验概率假设密度(PHD)分布产生的样本存在较大的偏差，导致该算法存在估计精度不高、粒子退化、滤波发散等问题。

针对以上问题，在深入分析P-PHDF的基础上，引入区间平滑算法(Rauch Tung Striebel smoother)[7-10]，提出基于区间平滑的粒子概率假设密度滤波(RTSP-PHDF)算法。

1粒子PHD滤波

1.1运动模型建立

设目标运动模型如下所示：

(1)

式(1)中：xk∈Rm和zk∈Rm分别为状态向量和量测向量，f(·)和h(·)分别表示状态转移方程和量测方程，wk-1、vk分别为系统过程噪声和量测噪声，服从均值为零，方差分别为Qk-1，Rk的高斯分布。

1.2PHD滤波描述

PHD滤波其本质是基于随机集(RSF)理论在Bayes框架下的一种扩展应用，其主要的区别在于PHD滤波是在递推运算概率假设密度，而Bayes滤波在递推运算后验概率密度。因此类比于Bayes滤波的预测方程以及更新方程：

PHD滤波预测方程：

Dk|k-1(xk|Zk-1)=γk(xk)+

∫[βk|k-1(xk|xk-1)+ek|k-1(xk-1)fk|k-1(xk|xk-1)]×

Dk-1|k-1(xk-1|Zk-1)dxk-1

(2)

PHD滤波更新方程：

(3)

式(2)、式(3)中：D(·)表示多目标概率假设密度，其在状态域上的积分为目标的个数，γk(xk)是新生目标强度，βk|k-1(xk|xk-1)源自xk-1的衍生目标强度，fk|k-1(xk|xk-1)是单目标状态转移密度函数，ek|k-1(xk-1)是目标存活概率，gk|k(zk|xk)为目标似然函数，PD(xk)为目标检测概率，Λk(z)=κk(z)+Ck(z)为量测z的强度，κk(z)是杂波强度，Ck(z)=∫pD(xk)gk|k(zk|xk)Dk|k-1(xk|Zk-1)dx表示似然函数的强度。

1.3P-PHDF滤波实现

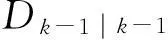
初始化：PHD滤波预测方程(2)经采样以后生成的粒子为：

(4)

权值更新：对于量测集中的每个量测z∈Zk，

(5)

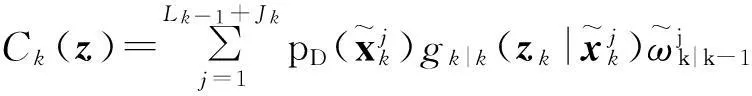
重采样：

对所有粒子权重求和得到目标个数：

(6)

将粒子集进行归一化：

(7)

对归一化粒子集进行重采样得到新的粒子集：

(8)

2RTSP-PHDF算法

2.1RTSP-PHDF算法基本思想

本算法针对P-PHDF重要性密度函数中没有包含量测提供的信息的问题，提出利用RTS引入k-T~T的所有量测值，对k-T时刻的粒子均值mk-T以及方差Pk-T进行修正，由此生成更加逼近系统真实PHD函数的重要性密度函数，以此来提高采样的质量，改善滤波算法的性能。

2.2RTSP-PHDF算法实现流程

RTSP-PHDF算法实现流程包括以下几个部分：状态向量扩维、初始化、单个粒子进行RTS、优化粒子权值更新以及重采样。

2.2.1状态向量扩维

扩维后的状态向量为：

(9)

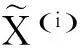
(10)

(11)

状态方程和量测方程变化为如下：

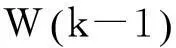
(12)

(13)

因此，可将平滑后的目标模型用下式表示：

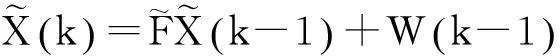
(14)

(15)

通过以上扩维将滤波和平滑结合在一起。

2.2.2初始化

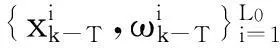
2.2.3单个粒子进行RTS

考虑到处理的往往是非线性滤波的问题，本文采用扩展卡尔曼(Extended Kalman Filter，EKF)对每一个粒子进行滤波。

状态预测和预测协方差为：

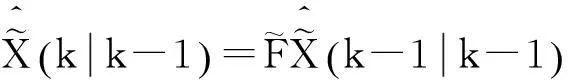
(16)

(17)

通过式(14)、式( 16)和式(17)，可得：

(18)

(19)

(20)

其中：i=1,2,…,T。

卡尔曼增益为：

(i=0,1,2,…,T)

(21)

残差和残差协方差为：

(22)

(23)

输出状态和协方差为：

(24)

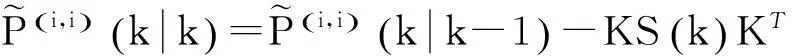
(25)

(i=1,2,…,T) (26)

2.2.4优化粒子权值更新

利用2.2.3中的得到的经优化的粒子：

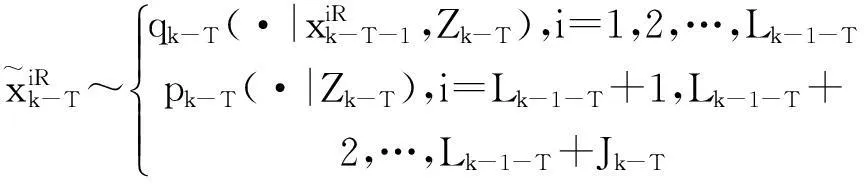
(27)

通过式(5)更新权值。

2.2.5重采样

综上所述整个算法流程如下：

步骤二：初始化，选取重要性函数并进行抽样。

步骤三：单个粒子进行RTS，获得每个粒子优化估计后的状态向量及其协方差。

步骤四：利用步骤三得到的优化粒子进行权值更新。

步骤五：重采样后回到步骤三进行下一时刻的粒子滤波运算，如此循环直到计算结束。

3仿真实验与对比分析

为了验证算法的有效性，利用Matlab对P-PHDF算法以及RTSP-PHDF算法进行仿真比较实验。实验在二维直角坐标系下观测区域为：[0,8 000]m×[-4 000,4 000]m，采样周期t=1s，仿真时间为50 s，观测雷达位于平面点[0,0]，平滑步长T=2，目标存活概率为1，检验概率为0.95，过程噪声w(k)为高斯白噪声，方差为5(m/s2)2，v(k)为量测噪声，方位角误差方差为0.05rad2，每个目标分配的粒子个数为1 000。

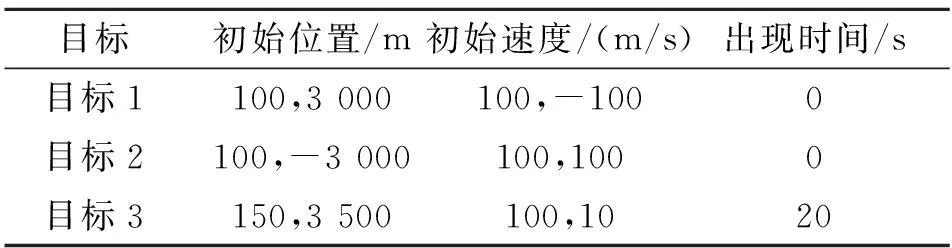
表1　目标初始位置和状态

目标跟踪模型如下：

X(k)=FX(k-1)+w(k)

(28)

式(28)为系统状态方程，X(k)为目标状态，F为状态转移矩阵，w(k)为过程噪声。

(29)

式(29)为量测方程， 其中v(k)为量测噪声，xst、yst为观测点的横纵坐标。

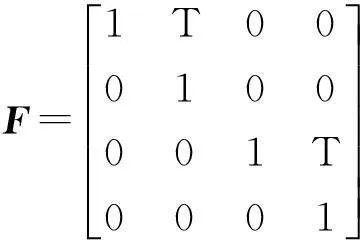
(30)

仿真结果如图1-图5所示。

图1为目标实际运动轨迹和仿真环境。图2为目标实际运动轨迹和P-PHDF估计值，可以明显看到P-PHDF 算法估计值偏离实际运动轨迹较大。图3为目标实际运动轨迹和RTSP-PHDF估计值，与图2相比较，可以明显看出RTSP-PHDF估计值更贴近于实际运动轨迹。图4为P-PHDF和RTSP-PHDF目标数目估计，在此方面两种算法都能准确估计目标数目。图5为P-PHDF和RTSP-PHDF多目标OSPA误差，从中可以看出P-PHDF多目标OSPA 误差距离均在50 m之上，甚至达到200 m，同时非常不稳定，波动性比较大；而RTSP-PHDF算法多目标OSPA 误差距离均在50 m以下，同时相比较而言比较平稳。表2为具体数值的比较，可以更清晰地看出RTSP-PHDF算法的平均OSPA误差相比较于P-PHDF算法，有很大减小，虽然在运行时间上有所增加，也在可承受范围内。综上所述，从各方面仿真结果比较看出，本文提出的RTSP-PHDF算法在杂波环境中，就估计精度以及跟踪系统稳定性两个方面而言，具有巨大的优势。

图1　目标实际运动轨迹和观测值Fig.1　True movement trajectoryand measurement value of target

图2　目标实际运动轨迹和P-PHDF估计值Fig.2　True movement trajectory andP-PHDF estimating value of target

图3　目标实际运动轨迹和RTSP-PHDF估计值Fig.3　True movement trajectory andRTSP-PHDF estimating value of target

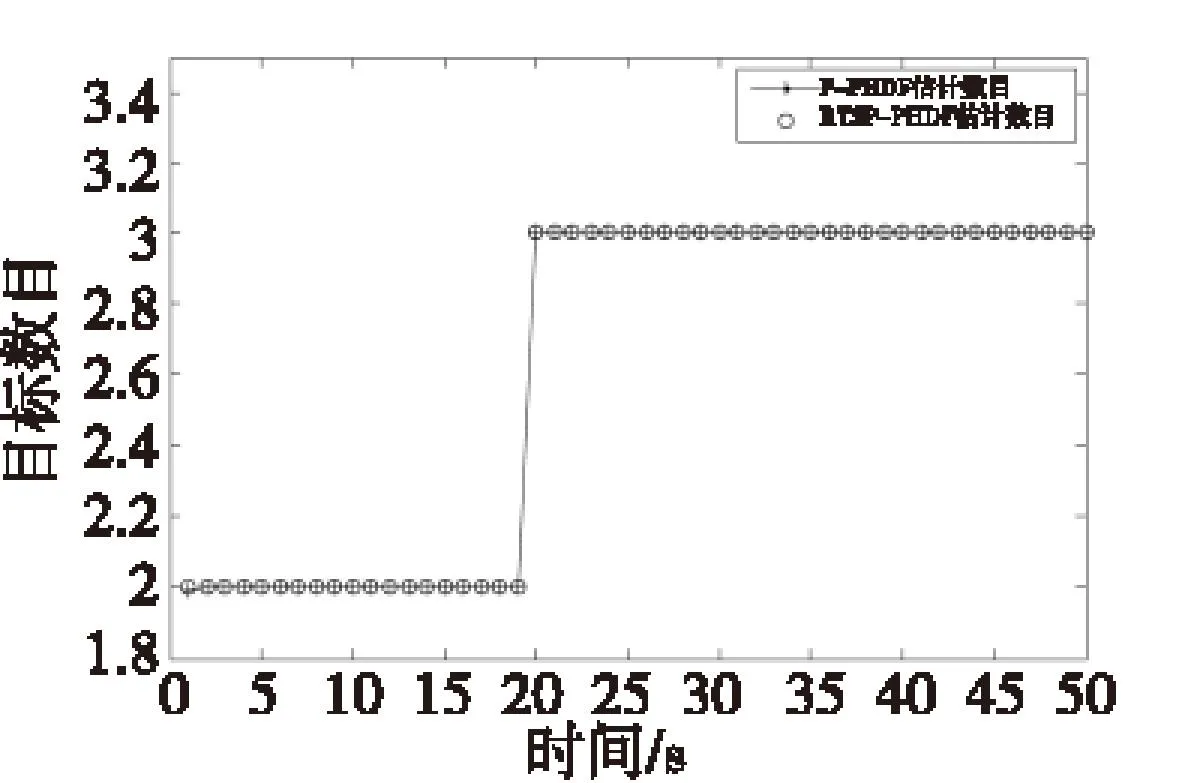
图4　P-PHDF和RTSP-PHDF目标数目估计Fig.4　Target number estimationof P-PHDF and RTSP-PHDF

图5　P-PHDF和RTSP-PHDF多目标OSPA误差Fig.5　Multi-target OSPA errorof P-PHDF and RTSP-PHDF

表2性能比照表

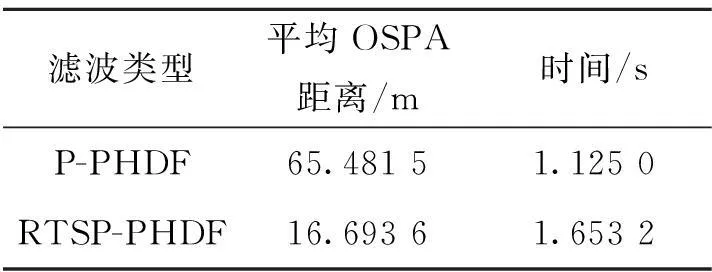
Tab.2　Performance comparation

4结论

本文提出了基于区间平滑的粒子概率假设密度滤波算法,在P-PHDF算法的基础上，结合RTS算法，将量测引入以优化重要性密度函数，构建优化重要性密度函数，使采样粒子分布更接近系统真实PHD分布，从而有效解决了P-PHDF算法仅仅在转移概率密度函数中采样引起的滤波精度低、滤波发散等一些问题。仿真实验表明了RTSP-PHDF算法保持了良好的滤波性能，是一种估计精度高的跟踪方法，具有较高的实用价值和广泛的应用前景。

需要指出的一点是，本文结合的RTS算法，在带来估计精度、稳定性的同时，也增加了计算强度，尤其在平滑步数增加的时候，计算强度增加更大，因此如何将RTS算法本身进行改进，在计算强度以及滤波精度之间寻找最佳的平衡点，是以后值得研究的问题。

参考文献:

[1]Mahler R. Statistical multisource multitarget information fusion [M]. USA: Artech House, 2007.

[2]Mahler R. Multi-target Bayes filtering via first-order multi-target moments [J]. Aerospace and Electronic Systems (S0018-9251), 2003, 39(4): 1152-1178.

[3]Vo B N, Singh S, Doucet A. Sequential Monte Carlo implementation of the PHD filter for multitarget tracking [C] //Proc. Int’l Conf. on Information Fusion. Cairns, Queensland, Australia: Melbourne University, 2003: 792-799.

[4] ZHAN Ronghui, WAN Jianwei.Iterated unscented Kalman filter for passive target tracking[J]. IEEE Transactions on Aerosp-ace and Electronic Systems,2007,43(3):1155-1163.

[5]孟凡彬,郝燕玲,张崇猛,等. 基于无迹粒子PHD滤波的序贯融合算法[J]. 系统工程与电子技术,2011,25(1):94-103.

[6]赵玲玲.目标跟踪中的粒子滤波与概率假设密度滤波研究[D].哈尔滨:哈尔滨工业大学，2011.

[7] Rauch H E, Tung F, Striebel C T. Maximum likelihood estimates of linear dynamic systems [J]. Journal of American Institute of Aeronautics and Astronautics,1965,3(8):1445-1450

[8]曹蓓. 粒子滤波改进算法及其应用研究[D]. 西安：西安光学精密机械研究所,2013.

[9]王晓,韩崇昭,连峰.基于随机有限集的目标跟踪方法研究及最新进展[J].工程数学学报, 2012, 29(4):568-578.

[10]连峰. 基于随机有限集的多目标跟踪方法研究[D].西安: 西安交通大学,2009.

本 刊 声 明

中国知网发起设立的“学术不端文献检测中心”,其功能是以《中国学术文献网络出版总库》和大量国际学术文献为全文比对资源,辅助检查抄袭、一稿多投、不当署名、伪造、篡改等学术不端行为。我刊作为中国知网的合作单位,有义务为净化学术空气,制止学术不端行为作出贡献,请各位读者、作者大力支持,与我们共同努力,从根本上铲除学术腐败的土壤,树立全民求真、求实的科学态度。

本刊编辑部

摘要:针对杂波情况下，粒子概率假设密度滤波(P-PHDF)算法存在估计精度低、滤波发散以及粒子退化等问题，提出基于区间平滑的粒子概率假设密度滤波(RTSP-PHDF)算法。该算法利用区间平滑算法(RTS)引入观测值优化重要性密度函数，使粒子分布更逼近多目标概率假设密度的分布，进而得到优化的采样结果，改善滤波性能。仿真结果表明，与P-PHDF算法相比，该算法在有效提高估计精度同时，进一步提高了跟踪系统稳定性。

关键词:随机有限集；区间平滑；粒子概率假设密度滤波

Particle Probability Hypothesis Density Filtering Algorithm Based on Interval SmoothingTONG Qian, LI Hongyan, MAO Shaofeng，JIAO Ling，HUANG MingJun

(Information and Navigation College, Air Force Engineering University, Xi’an 710077, China)

Abstract:In the presence of clutters, particle-probability hypothesis density filtering (P-PHDF) algorithm may cause low estimation precision, filter divergence and particle degeneracy, to solve these problems, a Rauch Tung Striebel smoother particle-probability hypothesis density filtering (RTSP-PHDF) algorithm was proposed. This algorithm exploited Rauch Tung Striebel smoother and introduced observation optimization importance density function, making particle distribution closer to multiple targets probability hypothesis density distribution and thus deducing optimized samples with improved filtering performance. The simulation revealed that, in comparison with P-PHDF algorithm, the proposed algorithm had increased estimation precision with further improved stability of tracking system.

Key words:random finite set; interval smoothing; particle-probability hypothesis density filtering

中图分类号:TN953

文献标志码:A

文章编号:1008-1194(2015)06-0087-05

作者简介:童骞(1991—)，男，湖南娄底人，硕士研究生，研究方向：目标跟踪。E-mail：tongqian866@sohu.com。

基金项目:CEMEE国家重点实验室开放基金项目资助(2014K0304B)；陕西省自然科学基金项目资助(2015JM6332)

*收稿日期:2015-06-03