基于混合高斯粒子滤波的OFDM频偏估计算法

杨霄鹏，黄　洋，杨朝阳,姚　昆，焦　玲

(空军工程大学信息与导航学院，陕西 西安　710077)



基于混合高斯粒子滤波的OFDM频偏估计算法

杨霄鹏，黄洋，杨朝阳,姚昆，焦玲

(空军工程大学信息与导航学院，陕西 西安710077)

0引言

正交频分复用(OFDM)系统由于其众多优点被广泛应用于多个无线标准，如IEEE802.11a/g、802.16、数字视频广播(Digital Video Broadcasting， DVB)、LTE、B3G等。然而OFDM系统需要子载波之间保持正交，尤其是在高速航空移动通信中，由于航空信道存在突出的时变特性和多普勒频移[1]，会引起载波频率偏移(CFO)，破坏子载波之间的正交性，产生严重的子载波间干扰(ICI)，使通信系统性能恶化。因此有必要采取措施来解决载波频率偏移问题，而有效的OFDM频偏估计算法成为解决这一问题的关键。

近年来已提出多种算法[1-6]，用于解决OFDM频偏估计问题。文献[2]提出的最大似然估计法(Maximum Likelihood Estimation, MLE)通过在频域插入两个连续的导频符号，接收端根据相邻符号的相位差估计频偏，该算法估计精度较高，但在大频偏、高阶调制时性能较差。通过将OFDM频偏估计问题建模为动态状态空间模型，利用滤波类算法估计频偏成为当前的研究热点。文献[3]利用扩展卡尔曼滤波(EKF)算法估计频偏，其在大频偏和高阶调制下性能优于MLE算法，但由于是对频偏估计的非线性方程进行一阶泰勒展开，线性化后利用KF递推求得状态估计，存在截断误差，从而必定会对估计精度产生影响，并且EKF算法存在易发散、不稳定、对初值敏感的缺点。针对这些缺陷，文献[4]研究了Sigma-Point卡尔曼滤波在OFDM频偏估计中的应用，其性能优于EKF算法。这是因为无迹卡尔曼滤波(UKF)通过无迹变换实现了对非线性函数概率分布上的近似，而不是线性化近似非线性函数本身，其统计特性可以精确到三阶[5]。但EKF、UKF频偏估计算法需提前知道噪声的统计信息。针对粒子滤波(Particle Filter，PF)算法无需已知噪声的统计信息，且OFDM频偏估计的观测方程为指数形式的强非线性系统，文献[6]研究了基于粒子滤波的频偏估计算法，PF算法较UKF估计精度高、收敛速度快，然而其存在粒子退化问题。文献[7]提出了基于高斯粒子滤波的OFDM频偏估计算法，高斯粒子滤波避免了重采样步骤，滤波精度高，但算法复杂度高，实时性较差。文献[8]将卡尔曼滤波与粒子滤波结合提出了混合高斯粒子滤波算法并将其应用于组合导航系统，混合算法能很好的适应该系统状态空间线性非线性混合的特点，从而提高滤波精度和实时性。

本文针对现有高斯粒子滤波OFDM频偏估计算法复杂度高、实时性较差的不足，结合OFDM系统状态空间线性非线性混合的特点，提出了一种新的基于混合高斯粒子滤波的OFDM频偏估计算法。

1OFDM频偏估计的非线性滤波模型

在OFDM系统中，假设其子载波数为N，经过符号映射后的发送数据为X(k)，0≤k≤N-1，经过离散逆傅里叶变换后得到的时域发射信号为：

(1)

添加长度不小于最大多径时延的循环前缀，接收端去掉循环前缀后的接收信号y(n)可表示如下：

(2)

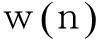
(3)

式(3)中,a表示中间状态变量，z表示观测量，g表示状态转移方程，f表示观测方程，v、w分别表示过程噪声和观测噪声。

通常情况下，频偏的变化速率并不快，因此可假设在单个数据帧中频偏为一常量。这种假设在包传输系统中是成立的，例如在无线局域网络(Wireless Local Area Network, WLAN)系统中，数据包设计的较短，这足以假设在一个数据包持续时间内载波频偏为一常量[3]。假设X(k)为接收端已知的训练符号，对应的时域信号x(n)为其傅里叶逆变换后的发射信号。为了分析推导方便，假设信道为高斯信道。至此，根据式(4)可以建立OFDM系统频偏估计的动态状态空间模型(Dynamic State-Space Model，DSSM)：

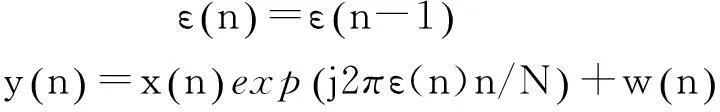
(4)

在通信终端高速运动环境下，例如航空移动通信。飞行器变速运动时，此时的频偏为时变频偏，此时频偏估计DSSM模型需要更为精确的描述。可以采用一阶自回归(AR1)模型来模拟载波频偏的变化[9]，时变频偏下的状态方程和观测方程表示如下：

(5)

通过分析式(5)可以得到频偏估计的动态状态空间模型的观测方程为指数函数形式的强非线性系统，如果采用扩展卡尔曼滤波类方法，其本身存在的截断效应会导致较大的估计误差，且存在滤波发散、稳定性差、对初值敏感等缺陷，从而不能达到准确估计载波频偏的目的。基于此，本文采用粒子滤波的改进算法，即高斯粒子滤波来估计频偏，针对频偏估计的状态空间线性、非线性混合模型的特点，将线性卡尔曼滤波引入高斯粒子滤波，达到进一步降低滤波复杂度，提高系统实时性的目的。

2粒子滤波算法

粒子滤波算法属于贝叶斯框架下的蒙特卡罗方法。其基本思想是：首先根据系统状态变量的经验条件分布，通过在状态空间产生一组随机样本点(即粒子)及其每个粒子对应的权值，并以均值代替积分运算，根据得到的观测数据不停的调整粒子的权重和位置用来修正最初的条件分布。

考虑如式(4)的OFDM频偏估计的非线性状态空间模型。

假设n时刻的频偏状态变量的集合为ε0:n={ε0,ε1,…,εn}，观测向量的数据集合为y0:n={y0,y1,…,yn}。根据贝叶斯估计的原理，状态量n时刻的后验概率密度可表示为如下：

(6)

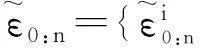
(7)

式(7)中，δ(·)表示狄拉克函数。

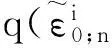
(8)

(9)

以上为序贯蒙特卡罗粒子滤波算法的基本原理，在实际应用中随着迭代的进行，除去一个粒子外，所有粒子都只具有微小的权重，重要性权值方差会随着时间的增加而变大，这样将会导致退化现象的发生。选择重要性函数和重采样方法是克服退化效应最有效的手段[10]。但是在实际应用中，一方面，大量粒子在处理非线性、非高斯问题时会存在计算复杂度高和大权值粒子反复被选择引起的粒子贫化效应问题。另一方面优化的重要性密度函数的获取与从目标函数分布中抽取样本的困难程度完全等同。为了解决这一问题，可以选择高斯分布函数来构造重要性密度函数，即采用高斯分布来产生下一个预测粒子。通过高斯密度函数来近似滤波概率分布，将最新的观测数据融入到了系统的状态转移过程中，这样产生的预测样本非常接近于状态真实后验概率的样本。高斯粒子滤波器适用于非线性、非高斯系统环境，具有较高的滤波精度，算法简单稳定性强，避免了重采样步骤且不存在粒子退化现象，实时性好，易于超大规模集成电路实现[11]。

3快速采样混合高斯粒子滤波的频偏估计器

高斯粒子滤波的核心思想是假定被估计的状态变量后验概率密度函数近似服从高斯分布，然后利用粒子滤波算法求解高斯分布的相关参数以得到状态的估计值。高斯粒子滤波的目的是通过一群粒子及其相应的权值来得到系统的滤波密度函数p(ε|y1:n)。一般情况下服从高斯分布的随机变量ε的概率密度函数可表示如下：

μ)Σ-1(ε-μ)/2])

(10)

式(10)中，μ表示m维向量ε的均值，Σ为ε的协方差阵。

高斯粒子滤波可以表述如下：

GPF测量更新过程：当获得k时刻的观测值yk后，滤波密度函数可以表示如下：

式(11)中，Ck=(∫p(εk|y0:k-1)p(yk|εk)dεk)-1为归一化因子。滤波概率密度可以近似为如下形式的高斯分布：

p(εk|y0:k)≈N(εk;μk,Σk)

(12)

GPF的时间更新过程：通过在k时刻从概率密度p(εk+1|εk)中采样，则可得

(13)

把p(εk+1|y0:k)近似为如下所示的高斯分布：

(14)

高斯分布参数的获取是通过对样本及其权值计算得到的。本文所解决的问题中，OFDM的频偏估计的状态空间模型状态方程为线性，观测方程为非线性的混合模型。针对这种具体应用环境，可以采用混合粒子滤波算法进行求解。混合粒子滤波算法的核心思想是：对状态方程的线性部分采用KF的线性递推方式取代高斯粒子滤波中的更新方式，对非线性部分保留高斯粒子滤波递推方式。

基于混合高斯粒子滤波的OFDM频偏估计算法步骤如下：

1)初始化

通过选取合适的参数，使粒子服从参数为N(ε0,μ0,Σ0)的正态分布。

2)时间更新

(15)

3)量测更新

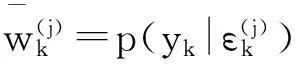
(16)

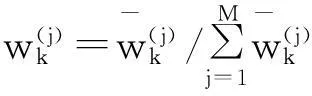
(17)

4)计算滤波结果和相关参数

根据之前的采样粒子及其对应的权值计算滤波结果和高斯分布参数，从而使得量测更新后的粒子服从N(εk,μk,Σk)正态分布，状态频偏的滤波值估计值μk及其对应的方差Σk可由下式计算：

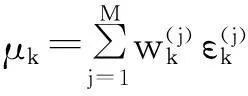
(18)

(19)

返回步骤2)，循环以上步骤。

以上为基于混合高斯粒子滤波算法的OFDM频偏估计的算法步骤。通过对步骤2)时间更新过程的分析可以发现，改进后的GPF算法只需更新高斯分布参数和方差，不需要对每个粒子逐个更新，因此改进后的GPF算法计算量较低，并且对于线性系统而言，KF状态更新过程为最优估计，所以其在降低复杂度的同时保证了精度不会下降。

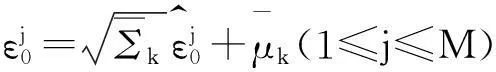
(20)

4仿真分析

为了验证改进的混合高斯粒子滤波的算法的性能，分别在如式(4)和式(5)所示的模型下进行了仿真分析，并对比分析了UKF、GPF和本文所提频偏估计算法的性能。OFDM系统参数设置为：子载波数N=64，训练序列采用PN序列，长度为64，归一化载波频偏为ε=0.25，AR1模型初始频偏ε0=0.25，采用16QAM高阶调制，加性高斯白噪声信道，频偏初值不失一般性设置为0.01。

图1为信噪比SNR=15 dB，GPF算法和本文算法中粒子数均取M=200，16QAM调制下，固定频偏模型和和时变频偏一阶AR模型下的频偏估计曲线。通过观察收敛曲线(a)的变化趋势可以发现，GPF和本文频偏估计算法较UKF频偏估计算法收敛速度更快，精度更高。GPF和本文算法大约在第10步左右即可收敛到真实频偏，而UKF算法需要25步左右才可收敛到频偏真实值附近。而通过图1(b)可以进一步发现GPF和本文算法在对时变频偏的跟踪方面性能更优，估计精度更高。

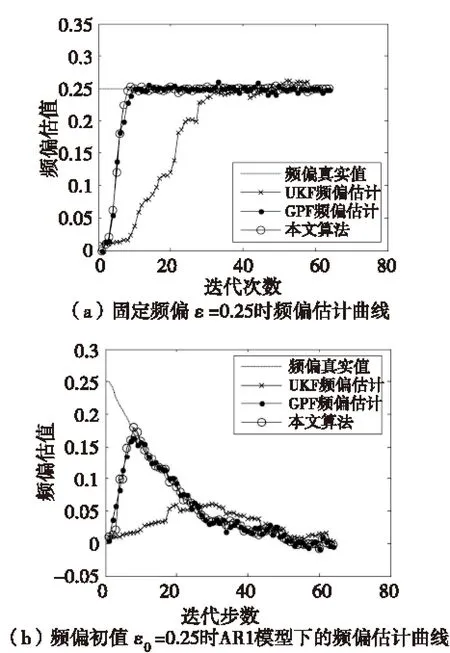
图1　三种频偏估计算法收敛曲线比较Fig.1　Comparison of three carrier frequency offsetestimation algorithms convergence curve

图2为信噪比SNR=15 dB，16QAM调制下频偏纠正前后的星座图。对比收发前后的信号星座图可以发现，由于频偏的存在使得星座图发生了严重的相位旋转和畸变，导致解调出错，通信性能恶化。经过频偏估计和补偿后相位旋转得到了纠正，星座图紧凑清晰。

定义频偏估计的均方误差(Minimum, Square, Error, MSE)为：

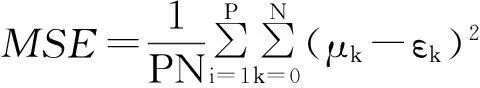
(21)

式(21)中，P为蒙特卡罗仿真的次数，N为子载波个数，μk为频偏估计估值，εk为频偏真实值。

图2　信号纠偏前后的星座图Fig.2　Signal constellation with frequency offsetand frequency offset compensation results

图3为16QAM调制，粒子数M=200，P取1 000时，三种算法的频偏估计MSE随信噪比(Signal Noise Ratio, SNR)性能曲线。表1为同一参数下，两种算法在单次运行中的时间比较，以此来验证本文算法的计算复杂度较低的优点。从图3可以看出基于确定性采样的UKF频偏估计算法的估计精度较基于随机采样的GPF和本文提出的快速采样混合算法要低。本文提出的基于混合高斯粒子滤波的算法的频偏估计精度和文献[6]中基于GPF滤波的频偏估计算法性能十分接近。而通过表1可以得到，本文算法较GPF滤波算法运行时间明显减少，计算复杂度有所降低，这与前面理论分析一致。

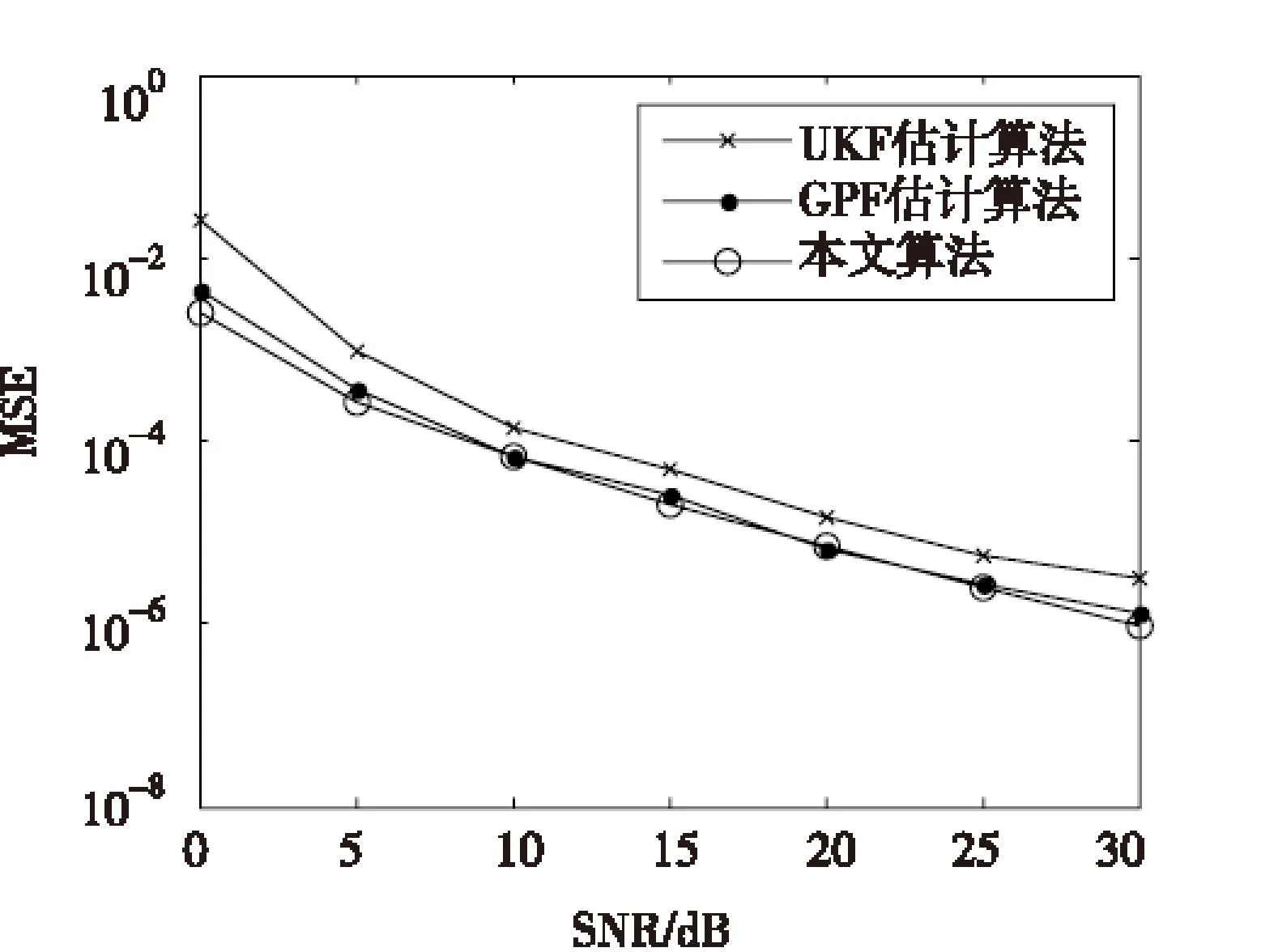
图3　频偏估计的MSE曲线Fig.3　The MSE property of four kinds of algorithms

算法运行时间/sGPF频偏估计0.1063本文算法0.0781

5结论

本文提出了基于混合高斯粒子滤波的OFDM频偏估计算法。该算法根据OFDM系统频偏估计线性、非线性混和模型的特点，其中状态更新过程采用KF滤波更新方式，直接更新高斯分布参数而非逐个粒子进行更新，有效地降低了滤波复杂度。在量测更新阶段通过线性变换法生成需要服从特定参数的高斯分布粒子群，相比于传统采样算法，计算复杂度降低。仿真实验和分析表明，该算法在保证滤波精度、快速收敛的同时有效地减少了算法运行时间，提高了系统的实时性。

参考文献:

[1]陈强, 杨霄鹏, 欧阳超，等. 基于TD-NLMS的航空移动通信OFDM系统载波频率偏移消除[J]. 空军工程大学学报(自然科学版), 2013, 14(1):71-74.

[2]YU J H, SU Y T. Pilot-assisted maximum-likelihood frequency-offset estimation for OFDM systems[J]. IEEE Transactions on Communications. 2004, 52(11): 1997-2008.

[3]Alex P. Palamides and Andreas M. Maras. A Bayesian state-space approach to combat inter-carrier interference in OFDM systems[J]. IEEE signal processing letters, 2007, 14(10):677-679.

[4]张鑫明,叶锋,杨波，等.Sigma-Point卡尔曼滤波用于OFDM载波频偏估计[J].天津大学学报(自然科学与工程技术版),2013,46(5):458-462.

[5]Julier S J, Uhlmann J K. A new method for the nonlinear transformation of means and covariances in filters and estimators[J]. IEEE Trans on Automatic Control, 2000,45(3): 477-482.

[6]Jaechan Lim， Daehyoung Hong. Frequency -selective and nonlinear channel estimation with unknown noise statistics[J]. IEEE communications letters,2010,14(3):245-247.

[7]Jaechan Lim， Daehyoung Hong. Gaussian particle filtering approach for carrier frequency offset estimation in OFDM systems[J]. IEEE signal processing letters, 2013, 20(4):367-370.

[8]熊剑, 郭杭, 熊智,等.GPS/INS组合导航系统中的高斯粒子滤波混合算法[J].中国惯性技术学报,2012,20(2):225-229.

[9]Eric Pierre Simon, Hussein Hijazi, Laurent Ros, et al. Joint estimation of carrier frequency offset and channel complex gains for OFDM systems in fast time-varying vehicular environment[C]//IEEE International Conference on Communications(ICC). Cape Town: IEEE Press, 2010:1-5.

[10]Jayesh H Kotecha, Petar M. Gaussian particle filtering[J]. IEEE Transactions on signal processing, 2003, 51(10):2592-2601.

[11]赵琳, 王小旭, 李亮，等. 非线性系统滤波理论[M]. 北京:国防工业出版社,2012:181-182.

[12]陈鹏,钱徽,朱淼良.一种快速高斯粒子滤波算法[J].华中科技大学学报(自然科学版), 2009,36(S1):291-294.

摘要:针对现有正交频分复用(OFDM)系统高斯粒子滤波频偏估计算法复杂度高、实时性较差的不足，结合OFDM系统状态空间线性非线性混合的特点，提出了一种新的基于混合高斯粒子滤波的OFDM频偏估计算法。该算法采用状态空间模型对其进行了建模分析，通过将卡尔曼滤波与高斯粒子滤波相结合，在时间更新阶段直接更新高斯分布参数代替逐个粒子更新，在量测更新阶段采用线性变换法生成采样粒子群代替传统高斯采样过程，降低了滤波复杂度，避免了粒子退化和贫化问题。仿真实验和分析表明，该算法在保证滤波精度、快速收敛的同时有效地减少了算法运行时间，提高了系统实时性。

关键词:正交频分复用；多普勒效应；频偏估计；高斯粒子滤波；快速采样

Carrier Frequency Offset Algorithm in OFDM Systems Based on Hybrid Gaussian Particle FilteringYANG Xiaopeng, HUANG Yang, YANG Chaoyang，YAO Kun, JIAO Ling

(School of Information and Navigation, Air Force Engineering University, Xi’an 710077, China)

Abstract:To solve the problems of high complexity, poor real-time of the Gauss particle filter carrier frequency offset estimation algorithm, for the property of OFDM system state-space model linearity and nonlinearity, a new fast sampling hybrid Gaussian particle filtering algorithm was proposed. Kalman filtering was combined with Gaussian particle filtering. During the time updating process, the parameters of Gaussian distribution was updated by instead of the each particle updating. During the measurement updating process, the linear transformation method was adopted to produce particles instead of traditional Gaussian sampling particle method. The complexity was decreased effectively and the particle impoverishment and dilution effect were avoided. The simulation results demonstrate the proposed algorithm while ensuring the accuracy and convergence speed, and could reduce the complexity and improve the real-time property.

Key words:orthogonal frequency-division multiplexing; Doppler effect; frequency offset estimation; Gaussian particle filtering; fast sampling

中图分类号:TN911.7

文献标志码:A

文章编号：1008-1194(2015)06-0071-06

作者简介:杨霄鹏(1973—)，男，甘肃天水人，博士，副教授，研究方向：宽带无线通信，信号处理。E-mail:hyznhhy@qq.com。

基金项目:国家自然科学基金资助项目(61202490)；航空科学基金(2013ZC15008)

*收稿日期:2015-07-12