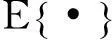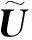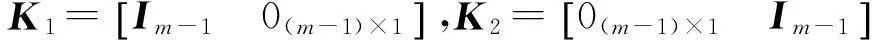基于空间平滑的单快拍波达方向估计算法

刘晓娣,周新力,肖金光

(海军航空工程学院电子信息工程系,山东 烟台　264001)



基于空间平滑的单快拍波达方向估计算法

刘晓娣,周新力,肖金光

(海军航空工程学院电子信息工程系,山东 烟台264001)

0引言

波达方向(DOA)估计在雷达、无线通信、声纳等领域有着广泛应用，经典的子空间类算法(如MUSIC算法[1]、ESPRIT算法[2])能够实现DOA的超分辨估计，但要求接收数据的协方差矩阵的秩等于信源个数，且估计的准确性以采用大量快拍数据获取高精度的信号子空间或噪声子空间为前提。而在实际应用中，相干信号普遍存在，且往往只能获得有限的快拍数据，尤其是在处理短时突发信号或运动目标信号时，只有单快拍可用，此时传统的DOA估计算法往往失效。

近年来，采用单次快拍数据的相干信源DOA估计得到关注[3-12]，并取得了一定的研究成果。文献[5]直接采用单次快拍数据构造Toeplitz矩阵实现DOA估计(简称DTOP)，实时性好；文献[6]在文献[5]的基础上，对单次快拍数据进行相关处理后再构造Toeplitz矩阵，提高了低信噪比条件下的DOA估计性能；文献[7]利用虚拟阵列接收数据构造伪协方差矩阵，并利用酉变换实现DOA估计，降低了计算复杂度。但文献[5-7]中的算法要求所有入射信号均具有零初始相位，这在实际应用中几乎无法满足[8]。文献[10]在文献[5]的基础上，以阵列的中心阵元作为参考阵元，利用单次快拍数据构造伪协方差矩阵实现DOA估计(简称ENDTOP)，克服了所有入射信号均需具有零初始相位的局限性，但该算法要处理M个信源，需要的接收阵元个数N≥2M-1，严重制约了其信号处理能力。文献[13]提出一种利用单次快拍接收信号重排的伪协方差矩阵构造模型，文献[5-6,10]的伪协方差矩阵构造方法可以统一在该模型下，该模型主要针对基于特征值分解的空间谱估计。

鉴于此，本文从实际应用出发，针对单次快拍情况下相干信源DOA估计的解相干和实时性问题，在经典空间平滑算法[14]的基础上，提出了基于空间平滑的单快拍DOA估计算法(SS-FBSS)。

1信号模型和空间平滑算法

1.1信号模型

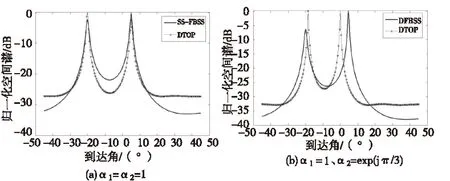
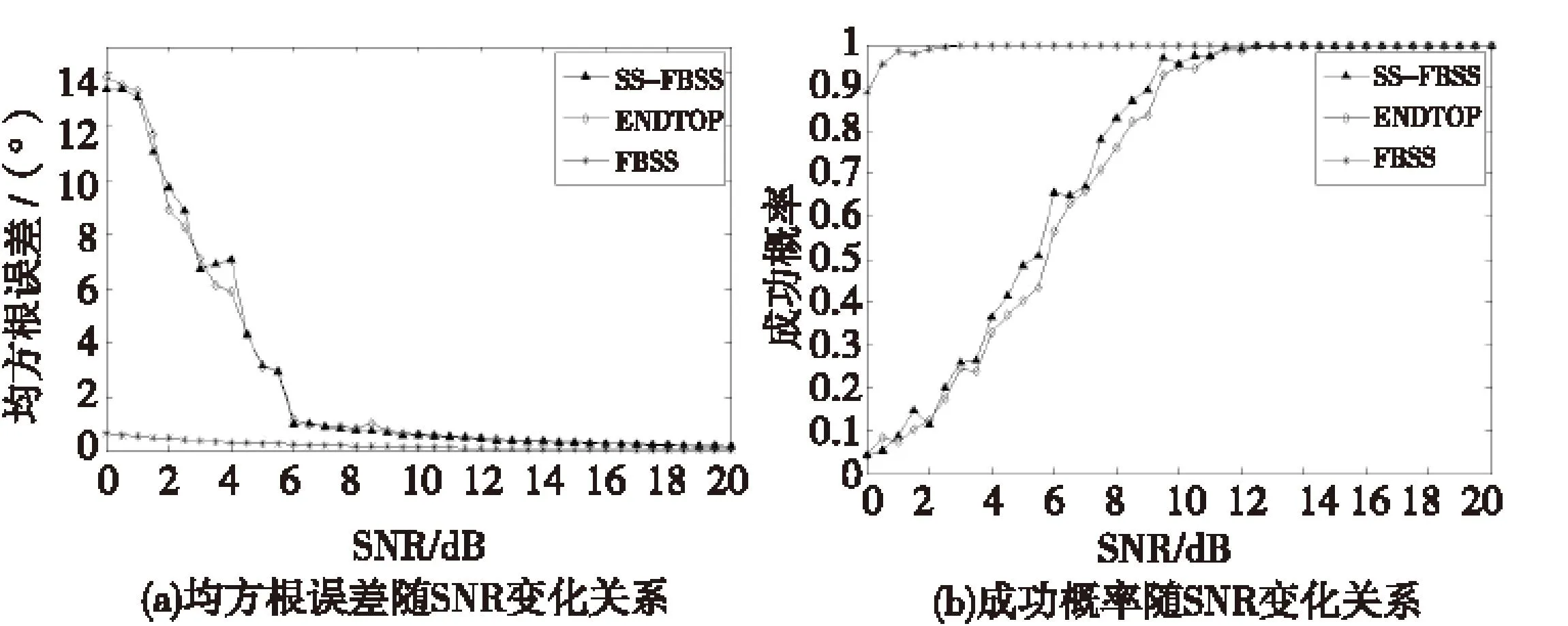
假设一个标准均匀线阵，包含N个相同的全向阵元，阵元间距d≤λ/2(λ是入射波长)。现有M个远场窄带信源(M

(1)

式(1)中，si(t)表示第i个窄带远场信号源，nk(t)表示第k阵元接收到的理想高斯白噪声。则阵列接收的数据可以表示为：

X(t)=[x1(t),x2(t),…,xN(t)]T=AS(t)+N(t)

(2)

假设前r个信源相干，

si(t)=αis1(t)(i=1,2,…,r)

(3)

其中复常数αi表示si(t)相对于s1(t)的相干系数。

阵列的协方差矩阵表示为:

(4)

1.2空间平滑算法

空间平滑算法[15]是目前一种有效的解相干算法，它利用均匀线阵的平移不变性，将一个N元均匀线阵分成相互重叠的l个子阵，每个子阵的阵元数为m，即有N=l+m-1。采用前向空间平滑算法得到l个子阵，如图1所示，对各个子阵的子协方差矩阵进行算术平均，得到前向空间平滑的协方差矩阵

(5)

前后向空间平滑(FBSS)的相关矩阵为：

(6)

式中J是反对角线元素为1的交换矩阵。

图1　前向空间平滑算法原理Fig.1　The method of forward spatial smoothingalgorithm

空间平滑算法是通过求解各个子阵协方差矩阵的均值来消除信源之间的相干性的，为保证计算精度，往往需采用大量快拍数据。

2基于空间平滑的单快拍DOA估计算法

考虑单次快拍情况下的解相干问题，同时提高算法的实时性，本文提出基于空间平滑的单快拍DOA估计算法(SS-FBSS)。

2.1基于空间平滑的单快拍数据解相干预处理

以第1个子阵为参考子阵，第k个子阵的接收数据为:

(7)

直接采用t时刻的单次快拍数据，以l个子阵的接收数据构造维数为m×l的矩阵

(8)

同理，采用后向空间平滑技术划分l个子阵，第i个子阵的接收数据为

(9)

采用t时刻的单次快拍数据进行后向空间平滑，以l个子阵构造维数为m×l的矩阵

(10)

式(10)中,J为反对角线元素为1的交换矩阵，下标为矩阵的维数。

利用式(8)、式(10)构造伪协方差矩阵：

(11)

(12)

2.2DOA估计

考虑R为centro-Hermitian矩阵，利用酉变换可将其转化成实矩阵。定义酉矩阵Q：

(13)

其中下标表示矩阵的维数，上述矩阵具有如下两个性质：

JQ*=Q

(14)

QQH=I

(15)

由式(13)定义的矩阵Q对伪协方差矩阵RG做酉变换

(16)

(17)

在此基础上，采用MUSIC、ESPRIT算法可实现DOA估计。

1)MUSIC算法

变换后的导向向量为:

(18)

利用式(17)、(18)求解MUSIC算法的谱估计表达式为[1]:

(19)

2)ESPRIT算法

根据文献[15]可知，对于复值的旋转不变性有K2US=K1USΨ，则实值的旋转不变性有

(20)

(21)

(22)

采用总体最小二乘法(TLS)求解式(20)可得Ψ′，对Ψ′进行特征值分解，有

(23)

2.3算法步骤总结

1)采用单次快拍数据根据式(8)、(10)、(11)构造centro-Hermitian伪协方差矩阵RG；

2)利用式(13)定义的酉矩阵，将伪协方差矩阵RG变换到实值空间T，如式(16)；

4)采用MUSIC或ESPRIT算法求解各个信号的入射角。

2.4算法性能分析

1)计算复杂度与前后向空间平滑[15]算法相比，本文提出的SS-FBSS算法直接采用单次快拍数据的空间平滑子阵构造伪协方差矩阵RG，而无需计算各个子阵的协方差矩阵，减小了运算量；并且该算法构造的伪协方差矩阵RG是centro-Hermitian矩阵，进行酉变换处理后，算法中的奇异值分解由原来的复数域变为实数域，计算复杂度大大降低。

2)分辨能力在SS-FBSS算法中，构造的伪协方差矩阵RG要实现“解相关”需要满足m≥M且2l≥M，而阵元数N=l+m-1。由此可知，当有M个信号源、每个子阵的阵元数为M+1时，要分辨这些信源，SS-FBSS算法需要阵元个数N≥1.5M，其分辨能力与FBSS算法一致，比ENDTOP算法高。但该算法也是通过降低自由度来实现解相干的。

3)估计精度SS-FBSS算法利用前后向空间平滑子阵构造伪协方差矩阵RG，克服了所有入射信号均具有零初始相位的局限性，且充分利用了单次快拍数据，估计精度高于DTOP算法、ENDTOP算法。

3数值仿真

仿真1假设一个均匀线阵，阵元数为5，阵元间距为λ/2。两个相干实值信号，θ1=-20°，θ2=5°，信噪比SNR为10dB，分别采用SS-FBSS算法和DTOP[6]算法进行解相干处理，而后采用MUSIC算法实现DOA估计。图2(a)、(b)分别给出了在α1=α2=1和α1=1、α2=exp(jπ/3)条件下，两种算法处理后的MUSIC谱图。由图2可以看出，当在α1=α2=1时，SS-FBSS算法与DTOP算法皆能实现解相干，而在α1=1、α2=exp(jπ/3)情况下，DTOP算法已经失效，而本文提出的SS-FBSS算法能准确地估计出波达角。这说明SS-FBSS算法克服了所有入射信号均具有零初始相位的局限性，无需对入射信号的初始相位作特别假定。

图2　SS-FBSS算法与DTOP算法的MUSIC谱图Fig.2　MUSIC spectrum of SS-FBSS and DTOP algorithms

仿真23个完全相干信源入射到均匀线阵，阵元数为15，阵元间隔为λ/2，入射角分别为θ1=-20°、θ2=5°、θ3=43°，信噪比SNR从0dB到20dB以0.5dB的间隔变化，分别采用SS-FBSS算法、ENDTOP[11]算法和FBSS算法[15]进行解相干处理，而后采用ESPRIT算法实现DOA估计。每个SNR做200次蒙特卡罗实验，其中FBSS算法采用150次快拍数据，仿真结果如图3所示，图3(a)为均方根误差随SNR变化曲线，图3(b)为成功概率随SNR变化曲线(成功概率定义为均方根误差小于0.2°的概率)。从图3中可以看出，本文提出的SS-FBSS算法的均方根误差、成功概率与ENDTOP算法基本一致，略优于ENDTOP算法。在低信噪比条件下，该算法的DOA估计误差较大，特别是信噪比在0～6dB时，随着信噪比的增大，均方根误差迅速减小，成功概率由不足10%迅速增大至65%。 而在信噪比大于6dB时，该算法的估计性能接近于采用150次快拍数据的FBSS算法。

图3　对完全相干信源的估计性能随SNR的变化曲线Fig.3　Estimation performance with SNR for coherent signals

仿真33个信源入射到一个均匀线阵，前两个为相干信源，α1=1、α2=exp(jπ/6)，第3个信源与第1个不相关，其他条件与仿真2相同，仿真结果如图4所示。从图4可以看出，该算法对部分相干信源的估计性能与对完全相干信源的估计性能基本一致，略优于ENDTOP算法，在低信噪比情况下估计误差较大，且随着信噪比的增大估计误差迅速减小。但在信噪比大于6dB时，该算法的估计性能接近于采用150次快拍数据的FBSS算法。通过比较图3与图4还可以发现，与完全相干信源相比，FBSS算法对部分相干且相干系数为复数的信源DOA估计性能明显降低，在低信噪比情况下，差异尤为明显。

图4　对部分相干信源的估计性能随SNR的变化曲线Fig.4　Estimation performance with SNR for partial coherent signals

4结论

本文提出了基于空间平滑的单快拍DOA估计算法。该算法直接采用单次快拍数据的前后向空间平滑子阵，构造centro-Hermitian伪协方差矩阵，实现解相干，而无需对入射信号的初始相位作特别假定，也无需计算各个子阵的协方差矩阵，减小了计算量；利用酉变换将复数域的奇异值分解实数化，降低了计算复杂度；最后结合MUSIC、ESPRIT等子空间类算法，实现了相干信源的DOA估计。数值仿真表明：该算法无需对入射信号的初始相位作特别假定；对于完全相干信源或部分相干信源，估计性能优于ENDTOP算法，且在信噪比大于6dB的情况下，接近于采用150次快拍数据的FBSS算法，能够有效实现单快拍DOA的快速估计，特别适用于对实时性要求较高的DOA估计场合。但该算法是通过降低自由度来实现解相干的，且在低信噪比情况下，估计误差较大，针对这些问题还需进一步研究。

参考文献:

[1]SchmidtRO.Multipleemitterlocationandsignalparameterestimation[J].IEEETransactionsonAntennasandPropagation, 1986,34(3): 276-280.

[2]RoyRKailathT.ESPRIT-estimationofsignalparametersviarotationalinvariancetechniques[J].IEEETransactionsonAcoustics,SpeechandSignalProcessing, 1989, 37(7): 984-995.

[3]AlcalaBE,RecioFR.Performanceanalysisofmetaheuristicapproachesforsingle-snapshotDOAestimation[J].IEEEAntennasandWirelessPropagationLetters, 2013, 12(1): 166-169.

[4]梁浩, 崔琛, 伍波, 等. 双基地MIMO雷达相干目标角度估计算法[J]. 系统工程与电子技术, 2014, 36(6): 1068-1074.

[5]谢鑫, 李国林, 刘华文. 采用单次快拍数据实现相干信号DOA估计[J]. 电子与信息学报, 2010, 32(3): 604-608.

[6]梁浩, 李小波, 王磊. 采用单次快拍数据实现信源DOA估计[J]. 数据采集与处理, 2013, 28(1): 58-63.

[7]闫金山, 彭秀艳, 王咸鹏. 基于酉变换的虚拟阵列DOA估计算法[J]. 哈尔滨工业大学学报, 2012, 44(4): 136-140.

[8]DelmasJP.Commentson‘ConjugateESPRIT(C-SPRIT)’ [J].IEEETransactionsonAntennasandPropagation, 2007, 55(2): 511.

[9]Jung-TaeKim,Sung-HoonMoon,DongSeogHan,etal.FastDOAestimationalgorithmusingpseudocovariancematrix[J].IEEETransactionsonAntennasandPropagation, 2005, 53(4): 1346-1351.

[10]王凌, 李国林, 谢鑫. 互耦效应下用单快拍数据实现相干信源完全解相干和解耦合[J]. 电子与信息学报, 2012, 34(10): 2532-2536.

[11]王凌, 李国林, 孟晶, 等. 用一次快拍数据实现二维完全解相干和解互耦[J]. 系统工程与电子技术, 2012, 34(11): 2208-2213.

[12]王凌, 李国林, 李静, 等. 一种新的单次快拍二维ESPRIT算法[J]. 北京理工大学学报, 2013, 33(1): 99-104.

[13]蒋柏峰, 吕晓德, 向茂生. 一种基于阵列接收信号重排的单快拍DOA估计方法[J]. 电子与信息学报, 2014, 36(6): 1334-1339.

[14]PillaiSU,KwonBH.Forward/backwardspatialsmoothingtechniquesforcoherentsignalidentification[J].IEEETransactionsonAcoustics,SpeechandSignalProcessing, 1989, 37(1): 8-15.

[15]王永良, 陈辉, 彭英宁, 等. 空间谱估计理论与算法[M]. 北京: 清华大学出版社, 2004: 199.

摘要:针对单次快拍情况下相干信源波达方向(DOA)估计的解相干和实时性问题，提出了基于空间平滑的单快拍DOA估计算法。该算法直接采用单次快拍数据的前后向空间平滑子阵，构造centro-Hermitian伪协方差矩阵，实现解相干，而无需对入射信号的初始相位作特别假定，也无需计算各个子阵的协方差矩阵，减小了计算量；利用酉变换将复数域的奇异值分解实数化，降低了计算复杂度；结合MUSIC、ESPRIT等子空间类算法，实现了相干信源的DOA估计。数值仿真表明该算法无需对入射信号的初始相位作特别假定，且对于相干信源能够有效实现单快拍DOA的快速估计，适用于对实时性要求较高的场合。

关键词:波达方向估计；相干信源；空间平滑；单次快拍；酉变换

Single Snapshot DOA Estimation Algorithm Based on Spatial SmoothingLIU Xiaodi, ZHOU Xinli, XIAO Jinguang

(Department of Electronic Information Engineering, Naval Aeronautics and Astronautics University, Yantai 264001, China)

Abstract:A direction-of-arrival (DOA) estimation algorithm based on spatial smoothing was proposed for the decorrelation and instant problems among DOA estimation of coherent signals when there was only one valid snapshot. The forward/backward spatial smoothing subarrays of single snapshot were directly used to construct the pseudocovariance matrix to accomplish decorrelation, which does not require that signals’ natural phases must be zero, and that the covariance of every subarray must be computed. The pseudocovariance, which was a centro-Hermitian matrix, was changed into real one by unitary transformation to reduce the computational complexity. Combined with the subspace kind algorithms such as MUSIC and ESPRIT, the DOA ccould be estimated. Simulation results showed that the algorithm did not require special assumption on signal’s natural phases, and could estimate the single snapshot DOAs of coherent signals effectively, which was suitable for real-time demand higher occasion.

Key words:direction-of-arrival estimation; coherent signals; spatial smoothing; single snapshot; unitary transformation

中图分类号:TN911.23

文献标志码:A

文章编号：1008-1194(2015)06-0066-05

作者简介:刘晓娣(1982—)，女，山东昌邑人，工程师，博士研究生，研究方向：无线电波传播、信号处理。E-mail：xdl_1982@163.com。

基金项目:国家自然科学基金项目资助(61179016)

*收稿日期:2015-04-12