两级线圈炮模拟引信后坐力方法

詹　超，雷　彬，向红军

(1.解放军军械工程学院，河北 石家庄　050003;2.总装备部西安军代局，陕西 西安　710032)



两级线圈炮模拟引信后坐力方法

詹超1,2，雷彬1，向红军1

(1.解放军军械工程学院，河北 石家庄050003;2.总装备部西安军代局，陕西 西安710032)

0引言

引信作为弹药的控制部分，其安全性和可靠性极其重要[1]。引信膛内安全性的考核一般分为靶场试验和实验室试验。实验室试验主要通过模拟引信膛内后坐和离心两种环境力对引信的性能进行测试。目前，引信后坐力动态模拟方法研究主要集中在基于气体炮的模拟方法[2-3]、用小型专用火箭弹模拟大型火箭弹的方法[4]以及利用离心力模拟后坐力的方法[5-6]。离心力模拟则主要通过对试验弹施加轴向转速来实现。近年来，电磁同步感应线圈发射器(线圈炮)作为一种新的驱动技术发展迅速[7-10]，已经验证其满足引信后坐力模拟试验的能量要求。采用单级线圈炮模拟引信膛内受力曲线时，由于只有一级，不需要考虑受力的连续性，但是无法模拟膛内受力时间较长的一类引信。为了克服单级线圈炮模拟引信膛内受力的这一不足，提出采用多级线圈炮发射装置模拟膛内时间较长的引信。在一般的多级线圈炮研究中，由于电枢出口速度是最重要的技术指标，对于受力的连续性没有要求，为了达到更高的发射效率，速度曲线一般呈脉冲状，即出现加速度接近零的时间段[11]。本文针对上述问题，提出了两级线圈炮模拟引信后坐力方法。

1线圈炮模拟引信后坐力要求

引信的后坐力模拟试验是指通过模拟引信发射过程中的膛压曲线，考察引信在这种受力状态下的安全性和解除保险的可靠性[12]。为了使多级电磁炮满足引信后坐力模拟要求，电磁炮推力曲线与引信在实际发射时的受力曲线完全相似。通常的近似条件有两个：一是模拟装置推力曲线与引信实际发射时的受力曲线大致相似；二是使引信在模拟装置和实际发射过程中受到的最大惯性力相等。

82 mm迫击炮榴弹膛压曲线如图1所示。膛压曲线与引信后坐力曲线趋势一致，这里以膛压曲线分析引信后坐力趋势和特点。一般研究分析中，典型多级线圈炮的电磁推力曲线如图2所示[13]。

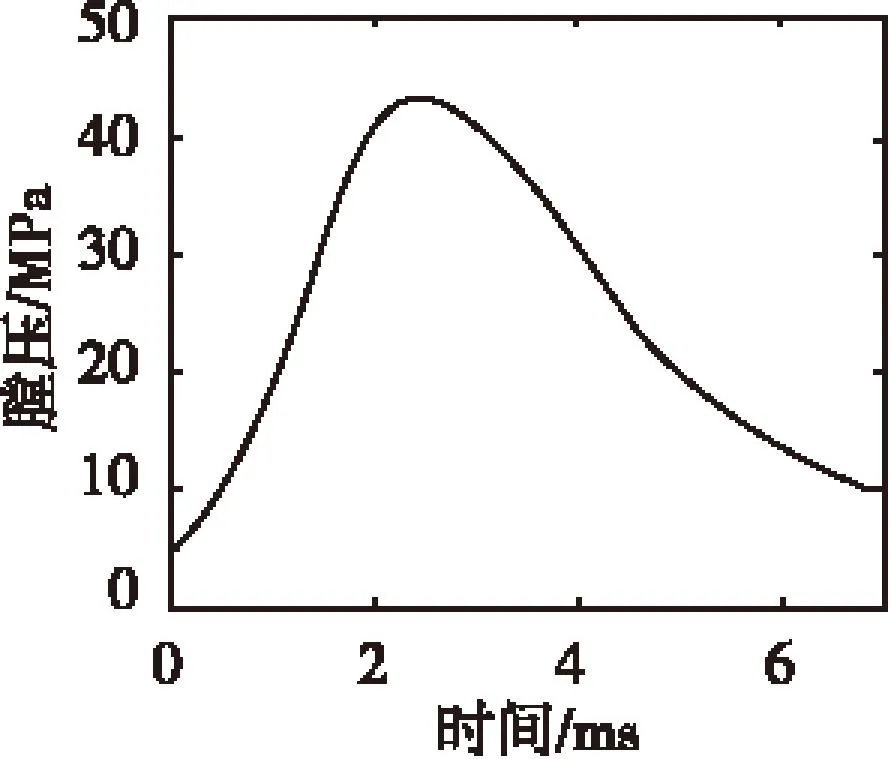
图1　82 mm迫击炮榴弹膛压曲线Fig.1　Chamber pressure curve of the 82 mm mortarhowitzer

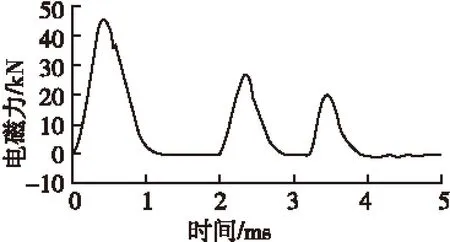
图2　多级线圈炮电磁推力曲线Fig.2　The electromagnetic curve of the multi-stagecoilgun

图1所示膛压曲线的特点是：引信在膛内受力时间约7 ms，膛压上升段较陡，下降段则较缓。图2中的电磁推力曲线由多次脉冲组成，并且单次受力时间只有1 ms，曲线上升下降都较快，显然图2中电磁推力曲线与图1中曲线存在较大差别，不满足引信后坐力模拟的要求。

2多级线圈炮模拟装置结构组成

所设计的多级线圈炮模拟装置模型如图3所示，主要由储能驱动线圈、电枢、电容器、同步触发控制电路、开关及试验弹等组成，发射时第一级首先馈电，然后其余各级驱动线圈依次馈电。图3中只给出了一级线圈的电源和控制电路。在驱动线圈和电枢的设计上，主要的变化是增大电枢长度，缩小驱动线圈各级之间的距离，并且每一级的触发位置的设定是以获得连续受力为前提。

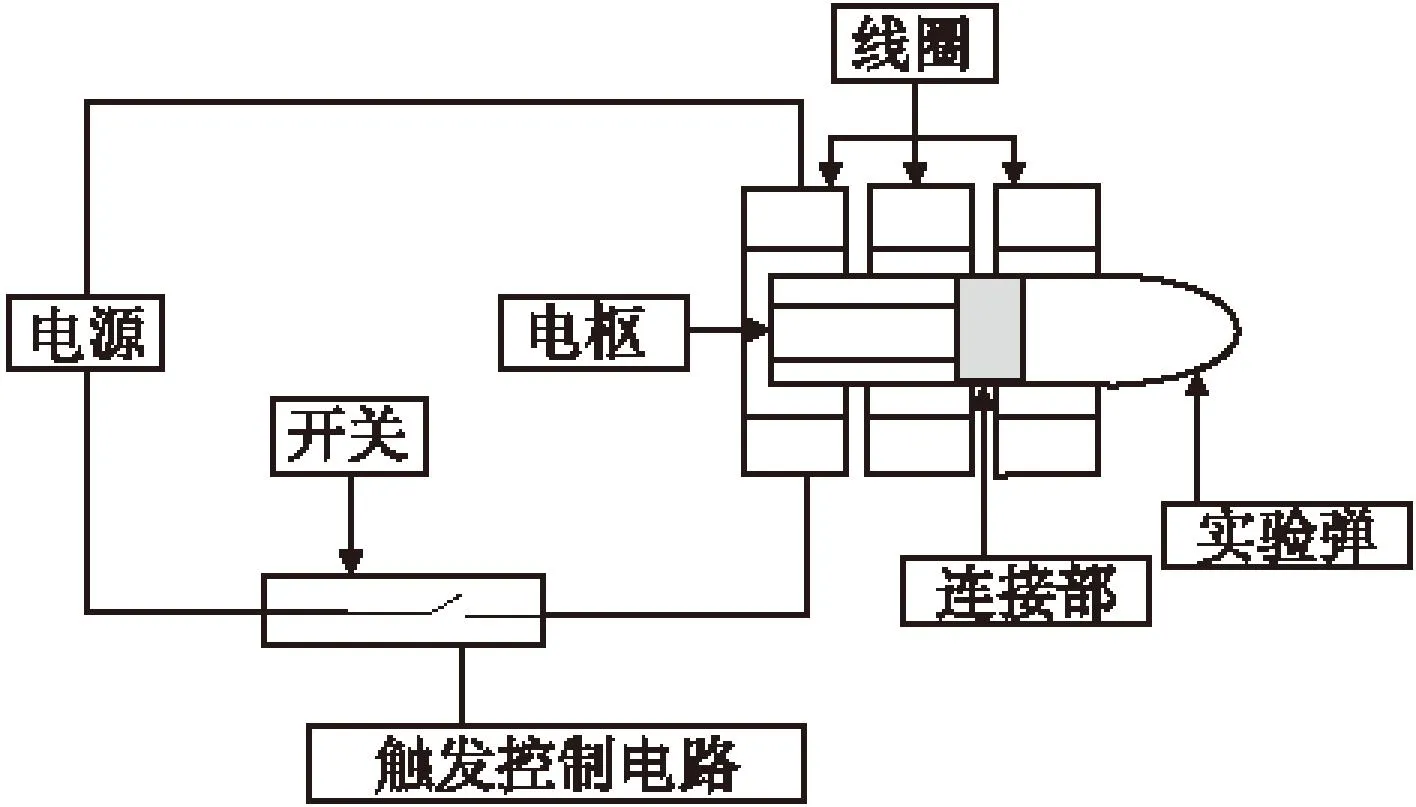
图3　多级线圈炮模拟装置结构示意图Fig.3　Schematic diagram of the structure ofthe simulationdevice with the multi-stage coilgun

电枢和驱动线圈的几何参数如表1所示。

表1　电枢和驱动线圈的几何参数

所有驱动线圈结构一致，电枢与驱动线圈的长度比为2，驱动线圈为多匝铜质线圈，电枢为铝质环状结构。本文以2级线圈发射器为例，通过有限元仿真，分析获得连续受力的条件及其影响因素。

3仿真及结果分析

3.1多级线圈炮模拟装置仿真验证

根据所设计的连续受力结构要求，建立2级线

圈炮有限元仿真模型。由于同步感应线圈发射器为轴对称结构，因此可简化为二维模型，既可以保证计算精度，又能够降低计算量[14]。仿真模型如图4所示。运动区域和求解区域的材料属性分别设为空气、真空。

仿真区域的网格剖分情况如图5所示，为了保证仿真计算精度和仿真速度，将电枢、两级驱动线圈及运动区域的网格划分得比较密集，而求解区域的网格划分相对比较稀疏。

驱动线圈与电枢作用的等效电路图如图6所示。电容器C充电电容为2 mF，充电电压为1 kV。驱动线圈的电阻R1设为100 mΩ，电枢的环路电阻R2设为10 mΩ。为了消耗驱动线圈的感应电流，在仿真电路中加入续流二极管D，以避免驱动线圈给脉冲储能电容器反向充电。第二级驱动线圈触发距离设为10 mm，即驱动线圈在运动10 mm后，第二级驱动线圈触发。

仿真的起始时间为0 ms，终止时间为3 ms，仿真时间步长为0.01 ms。电枢受力随时间的变化如图7所示。

1-第一级驱动线圈；2-第二级驱动线圈；3-电枢；4-运动域；5-求解区域图4　仿真模型Fig.4　The simulation model

图5　仿真区域的网格剖分Fig.5　The grid subdivisionof the simulation area

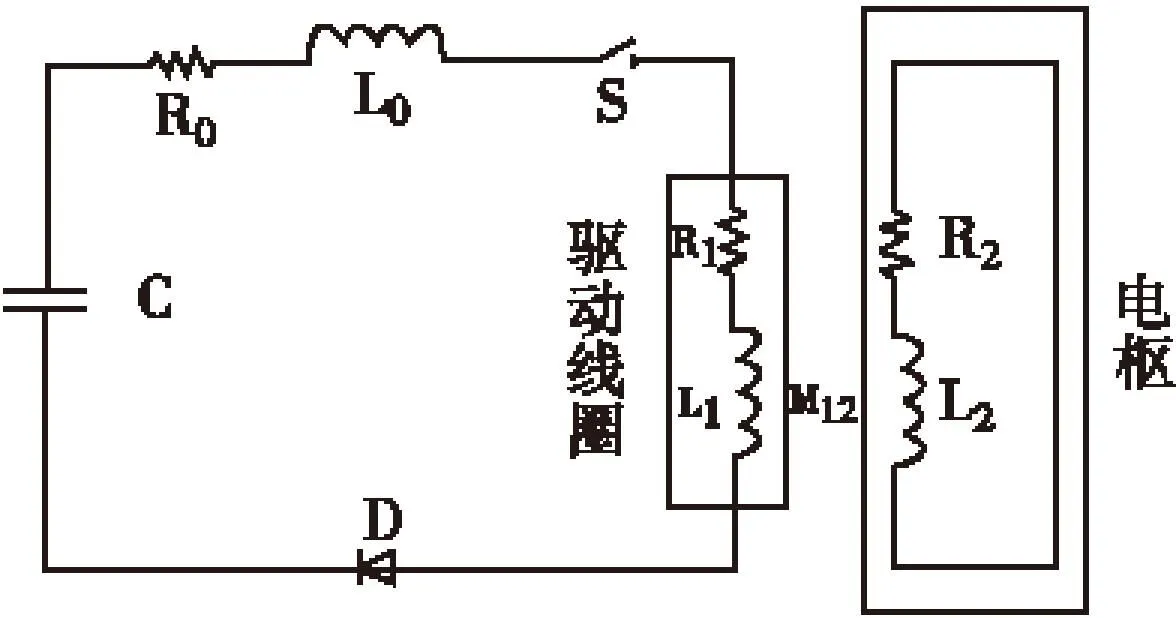
图6　驱动线圈与电枢作用的等效电路图Fig.6　The equivalent circuit diagtramof the interaction between the drivecoil and the armature

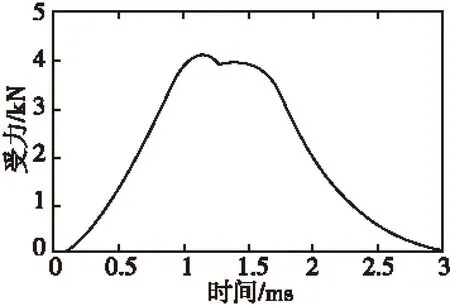
图7　电枢受力曲线Fig.7　The force curve of Armature

从图7中可以看出，两级电磁线圈作用到电枢上的力基本为单脉冲连续状态,最大受力为4 kN，受力曲线上升与下降过程基本对称。仿真结果表明，所设计的结构达到了要求，实现了两级线圈作用力的连续，克服了受力的多脉冲特点。如图7所示的受力曲线虽然在峰值附近有波动，但是受力时间增加，是引信后坐力模拟需要解决的问题之一，值得深入研究，下文主要对电枢受力曲线的影响因素进行研究。

3.2多级线圈炮模拟装置影响因素分析

对以下影响因素的分析都是以上一节中仿真模型为基础，以单变量研究方法进行分析。包括第二级触发距离、电枢与驱动线圈的长度比、驱动线圈级间距对受力连续性和持续时间的影响。

3.2.1第二级触发距离的影响

对于图4所示仿真模型，分析第二级线圈触发距离对受力的影响。触发距离是指前一级线圈触发到后一级线圈触发的时间段内电枢运动的距离，本文定义为S。在基本模型的基础上，改变触发距离S，数值如表2所示。

表2　触发距离

不同触发距离的受力曲线如图8所示。从图8中可以看出，随着第二级触发距离的增大，受力曲线产生突变的时刻延后，并且受力峰值减小。当S=2 mm 时，两级线圈受力的连续性最优，且受力峰值大幅增加，受力曲线尖锐。随着S的增大，平滑连续性越差。当S=8 mm时，电枢受力在峰值附近较为平滑，持续时间较长，受力曲线相对扁平。在下面的研究中，将对这两种情况进行分析。

不同触发距离下的电枢速度曲线如图9所示。

速度曲线反映了驱动系统对电枢的做工能力。从图9中可以看出，随着第二级触发距离的增加，驱动线圈对电枢的做工能力越弱。综上分析可知，触发距离直接影响第二级的触发时刻，主要表现在对两级电磁力叠加点的影响上。对于受力连续性而言，触发距离是影响受力能否连续的关键因素。

3.2.2驱动线圈与电枢长度比的影响

定义长度比R为电枢长度与驱动线圈长度的比值。分别以R=1.2、1.5和2对S=2 mm和S=8 mm的两种情况进行仿真分析，结果分析如下。

S=2 mm时，不同长度比下，电枢受力随时间的变化如图10所示。从图10中可以看出，随着R值得增大，受力的上升段越陡，受力峰值越大，受力的连续性没有被影响。三种情况下，峰值分别为5.44 kN、5.53 kN、5.63 kN。

通过与实际膛压曲线的对比可知，对于以上三种情况，当长度比R=2时，最适合引信模拟的要求。不同长度比下，电枢速度随时间的变化如图11所示。从图11中可以看出，长度比越大，速度有小幅增加。

S=8 mm时，电枢受力和速度随时间的变化如图12和图13所示。从图12可知，长度比对受力持续时间几乎没有影响，峰值附近变化较小。但是随着长度比的增大，受力峰值有小幅增大，分别为4.16 kN、4.24 kN、4.31 kN。由图13可知，在S=8 mm的情况下，长度比同样对速度的影响很小。

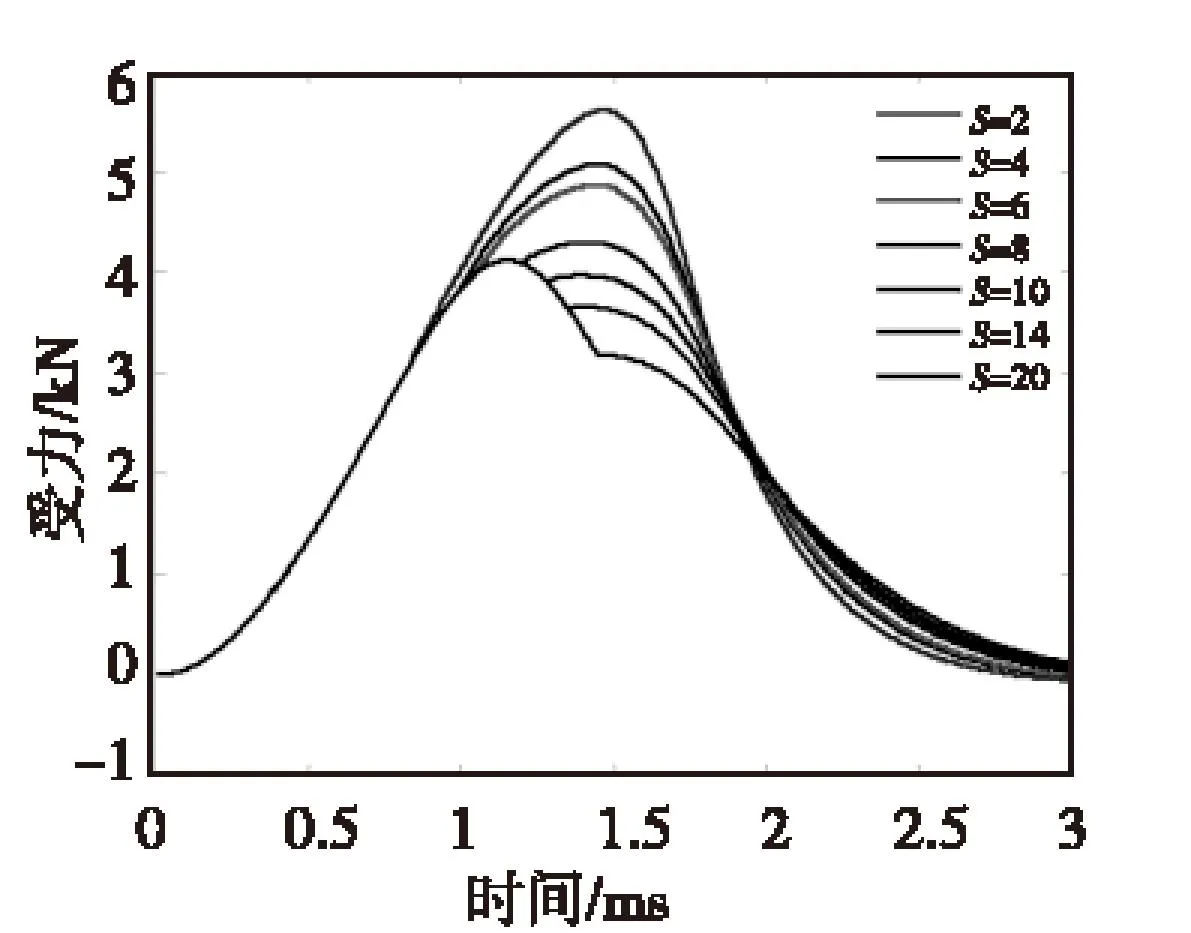
图8　不同触发距离的受力曲线Fig.8　The force curve of differenttriggering distance

图9　不同触发距离下的速度曲线Fig.9　Thespeed curve ofdifferent triggering distance

图10　S=2 mm下不同长度比的受力曲线Fig.10　The force curves ofdifferent length ratio when s=2 mm

图11　S=2 mm下不同长度比的速度曲线Fig.11　The speed curve of differentlength ratio when S=2 mm

图12　 S=8 mm下不同长度比的受力曲线Fig.12　The force curves ofdifferent length ratio when S=8 mm

图13　S=8 mm下不同长度比的速度曲线Fig.13　The speed curve of differentlength ratio when S=8 mm

综合上面的分析可知，长度比对受力连续性没有影响，对速度的影响也很小。在S=2 mm的情况下，长度比对上升沿有一定影响，对下降段的影响不明显；在S=8 mm的情况下，对受力峰值大小有一定影响。

3.2.3驱动线圈级间距的影响

驱动线圈级间距是指相邻两级线圈之间的距离，本文中定义L为级间距。同样，对S=2 mm和S=8 mm两种情况，以下表所示的L值进行仿真分析。

表3　驱动线圈级间距数值

S=2 mm时，不同级间距下，电枢受力曲线和速度曲线如图14和图15所示。由图14可知，随着L的增大，电枢受力曲线峰值出现时间靠后，但是峰值大小基本没有变化。全部受力曲线都呈现连续上升的趋势，随着L的增加，在第二级触发后，受力曲线的上升速度减缓，当L=20 mm时，出现持续时间约0.5 ms的平稳受力段。对于引信的模拟来说，受力连续上升的情况适合，即L=2 mm、4 mm、6 mm的三种情况适合引信后坐力模拟。由图15可以看出，L增大，加速能力越好。

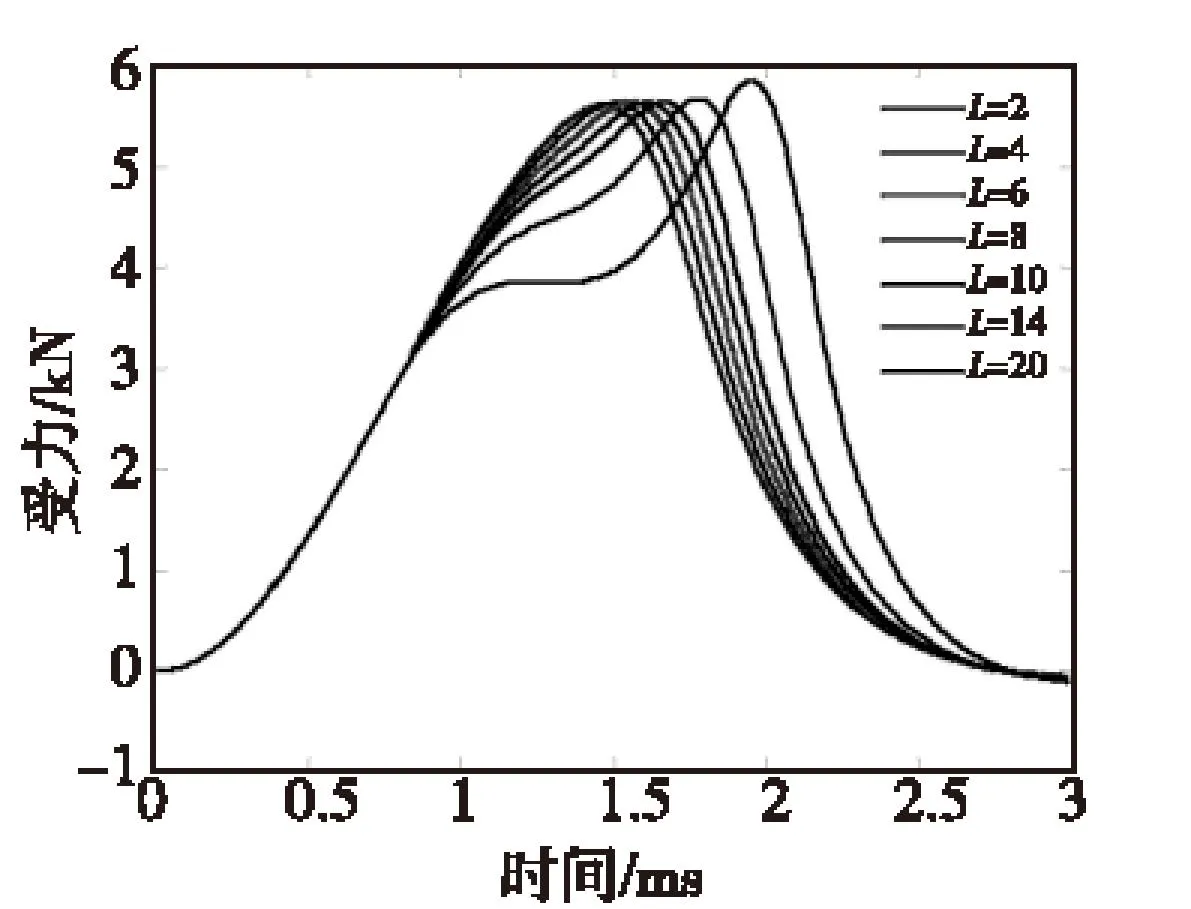
图14　S=2 mm下不同级间距的受力曲线Fig.14　The force curves of differentlevel spacing when S=2 mm

图15　S=2 mm下不同级间距的速度曲线Fig.15　The speed curve of differentlevel spacing when S=2 mm

S=10 mm时，不同级间距下，电枢受力曲线和速度曲线如图16和图17所示。由图16可知，当L为2、4、6、8、10 mm时，峰值附近保持时间稍有增大；L=14 mm和20 mm时， 受力峰值附近曲线上下波动较大。对于引信模拟来讲，前五种情况提高了受力峰值段的时间，更有利于引信膛内受力的模拟。由图17可知，随着L的增大，电枢速度提高，其表现和原因与情况S=2 mm相同，这里不作过多解释。综上，级间距的作用主要体现在对峰值段受力持续时间的影响上。在通过触发距离实现受力连续的前提下，调节级间距可以对受力峰值段作优化调整。

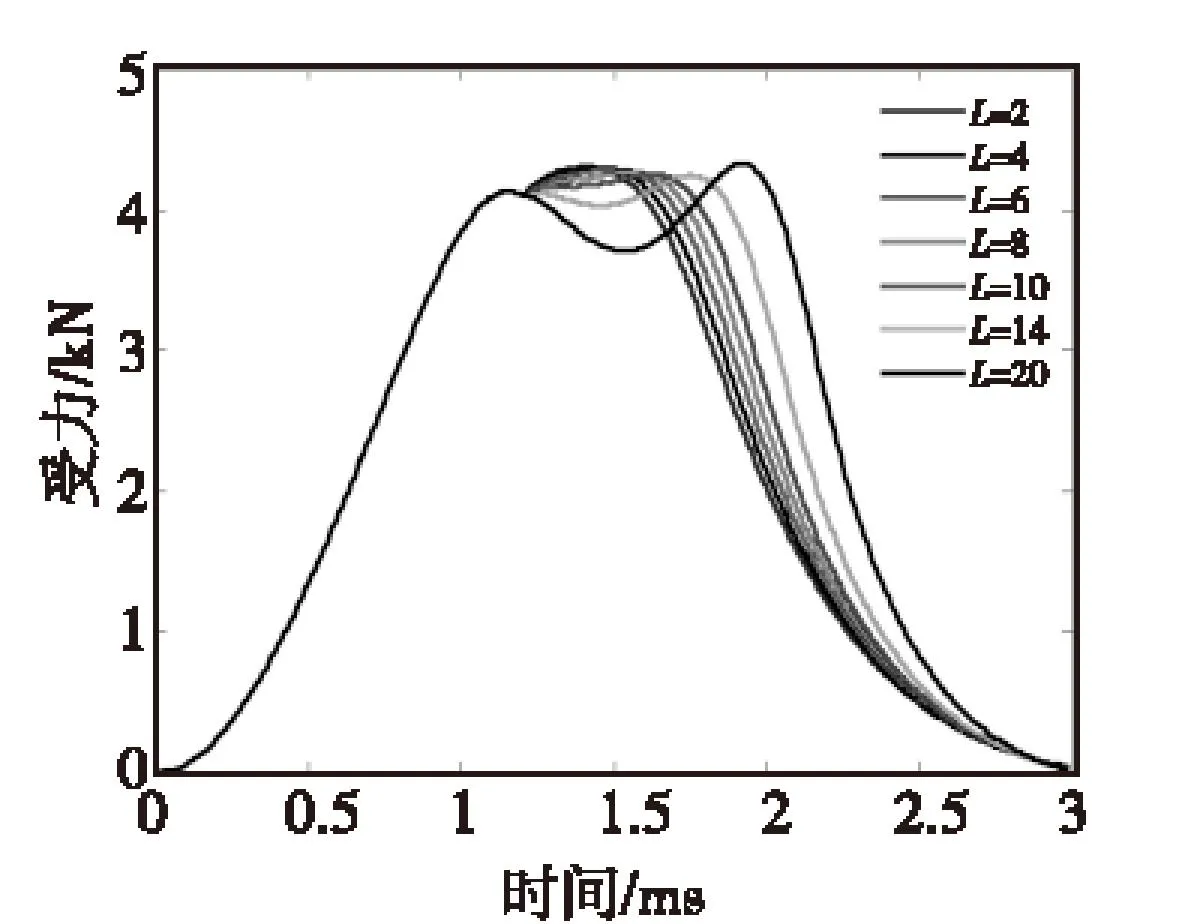
图16　S=8 mm下不同级间距的受力曲线Fig.16　The force curves ofdifferent level spacing when S=8 mm

图17　S=8 mm下不同级间距的速度曲线Fig.17　The speed curve of different level spacingwhen S=8 mm

4结论

本文提出了两级线圈炮模拟引信后坐力方法。该方法通过对传统两级线圈炮结构的改进，改变两级线圈受力呈多脉冲的特点，使其适应引信后坐力模拟的要求。仿真验证和结果分析表明，针对不同的引信及其模拟要求，可以通过调整线圈炮参数改变试验弹受力曲线，实现设备的多种模拟需求。拟针对具体引信型号，根据要求对两级线圈炮的参数设计和试验作进一步研究。

参考文献:

[1]张合. 引信机构学[M]. 北京: 北京理工大学出版社, 2007.

[2]齐杏林, 杨清熙, 文健, 等. 基于气体炮的引信动态模拟方法综述[J]. 探测与控制学报, 2011, 33(6): 1-4.

[3]杨清熙, 齐杏林, 赵志宁, 等. 撞击减速法模拟引信后坐加速度的影响因素[J]. 弹箭与制导学报, 2012, 32(3): 111-117.

[4]范安乐, 唐晓峰. 引信试验用模拟火箭弹[J]. 探测与控制学报, 2008, 30(3): 29-36.

[5]李来福, 王雨时, 闻泉. 引信经典后坐保险机构对过载时间的响应特性[J]. 四川兵工学报, 2014, 35(7): 147-152.

[6]安彦飞, 王雨时, 闻泉. 模拟后坐离心环境对惯性点火器钟表机构工作时间的影响[J]. 计算机辅助工程, 2013, 22(5): 91-95.

[7]Andrews J A. Coilgun Structures[J]. Magnetics, IEEE Transactions on, 1993, 29(1): 637-642.

[8]Kaye R, Turman B, Aubuchon M, et al. Induction Coil gun for EM Mortar[J]. IEEE Transactions on Magnetics, 2007, 43(1): 1810-1813.

[9]王莹,肖锋. 电炮原理[M]. 北京: 国防工业出版社, 1992.

[10]邹本贵, 曹延杰. 美军电磁线圈发射技术发展综述[J]. 微电机, 2011, 44(1): 86-89.

[11]向红军, 赵科义, 李治源, 等. 多级电磁感应线圈炮的级间耦合特性[J]. 高电压技术, 2012, 38(5): 1084-1089.

[12]张景玲,纪永祥. 引信试验鉴定技术[M]. 北京: 国防工业出版社, 2006.

[13]向红军, 李治源, 雷彬. 基于场路耦合的多级感应线圈炮内弹道分析[J]. 弹道学报, 2012, 24(3): 100-104.

[14]赵科义, 李治源, 程树康. 单级感应线圈炮工作过程的动态仿真[J]. 高电压技术, 2008, 35(8): 1667-1671.

摘要:针对单级线圈炮模拟引信后坐力受力时间不足，以及传统多级线圈炮电磁推力呈多脉冲状的问题，提出了两级线圈炮发射结构模拟引信后坐力的方法。该方法在电磁驱动部分通过增大电枢长度，缩小驱动线圈各级之间的距离，从而改变两级驱动线圈电磁力脉冲特点，使其适应引信后坐力模拟的要求。仿真验证和结果分析表明，该结构能够满足引信模拟的要求。针对不同的引信可以通过调整线圈炮参数改变试验弹受力曲线，实现设备的多种模拟需求。

关键词:电磁驱动；引信；后坐力模拟；连续受力；仿真

Two-stage Coilgun for Fuze Recoil SimulationZHAN Chao1, 2, LEI Bin1, XIANG Hongjun1

(1. Ordnance Engineering College, Shijiazhuang 050003, China；2. Xi’an Military

Representative Bureau of the General Equipment, Xi’an 710032, China)

Abstract:In order to overcome the problem of insufficient duration of the force which based on single-stage induction coil gun to simulate the recoil force of the fuze and electromagnetic curve, which is of multi pulse shape that produced from traditional multi-stage coilgun, a new method based on two-stage electromagnetic inductive coil gun to simulate the recoil of fuze was proposed. The method through increasing the length of the armature and narrowing the distance between the drive coil in the electromagnetic drive part, to change pulse characteristics of electromagnetic force, made it adapt to the requirement of fuze simulation recoil. Simulation results and analysis showed that this structure could satisfy the requirements of the fuze simulation. According to different fuze, force curve could be changed by adjusting the parameters of two-stage coilgun, to achieve a variety of simulation requirements of the device.

Key words:electromagnetic launcher; fuze; simulation of recoil; continuous force; simulation

中图分类号:TJ430.6；TM89

文献标志码:A

文章编号：1008-1194(2015)06-0012-05

作者简介:詹超(1991—),男，湖南桃江人，硕士研究生，研究方向：电磁发射与引信动态模拟试验技术。E-mail:zhanchao330@qq.com。

*收稿日期:2015-05-25