回声状态网络混沌跳频码预测方法

吕季杰，杨俊安，桂云川

(1.解放军电子工程学院，安徽 合肥　230037;2.安徽省电子制约技术重点实验室，安徽 合肥　230037)



回声状态网络混沌跳频码预测方法

吕季杰1,2，杨俊安1,2，桂云川1,2

(1.解放军电子工程学院，安徽 合肥230037;2.安徽省电子制约技术重点实验室，安徽 合肥230037)

0引言

跳频通信系统因其较强的抗侦察、抗截获能力而被广泛运用于军事通信。跳频通信系统的核心就是跳频码序列，常见跳频码序列一般由移位寄存器产生，例如m序列、RS序列等。近几年，随着对混沌理论的不断深入研究，利用混沌序列构造性能更加优良的跳频码成为业内首选。文献[1]研究指出，m序列、RS序列和混沌序列一样都具有混沌特性，即非周期、连续宽带频谱、类似噪声等特性。虽然具有混沌特性的跳频码多变复杂，但其本质上仍按照特定的规律产生，这也为跳频码预测奠定了理论基础。

为了准确地预测跳频码，人们构造了许多数学模型。支持向量机(Support Vector Machine)模型[2]建立在统计学理论和结构风险最小的基础上，根据样本数据寻求唯一的全局最优解，但其网络不具备反馈结构，缺乏记忆能力，降低了预测性能。贝叶斯网络(Bayesian Network)[3]是基于概率推理的图形化网络，通过一些变量的信息来获取其他变量的概率信息，达到预测的目的，但是贝叶斯网络中各个状态之间的概率关系较难获取，且训练过程复杂，增大了预测的难度。人工神经网络(Artificial Neural Networks)也被广泛运用在混沌时间序列领域，其中径向基网络(Radial Basis Function Network)[4]是一种前向神经网络，结构简单，且在全局和局部都能很好的逼近最优点，然而如果网络隐节点较多，则会导致过拟合现象，网络泛化性能变差；如果隐节点较少，则会导致欠拟合现象，网络泛化能力同样降低。传统递归神经网络(Recurrent Neural Network)[5]也比较适合用于跳频码预测，但是其运算量大，在预测过程中初始训练记忆也会逐渐消失，导致其在跳频码预测时出现准确率低、预测时间长等不足，限制了其在跳频码预测上的应用。本文针对上述问题，提出了回声状态网络混沌跳频码预测方法。

1回声状态网络

2001年Jager教授提出了回声状态网络[6](Echo State Network)，克服了传统递归神经网络的记忆减退、训练量大等问题，只训练输出连接权，大大减少了计算量，同时由于网络内部存在一个由成百上千个神经元稀疏连接的大型动态储备池，在数据训练过程中，通过改变网络各权值矩阵的数值大小，达到记忆数据的目的，对于时间序列预测有更好的效果。

1.1回声状态网络的数学模型

储备池是网络最重要的部分，由众多神经元稀疏连接而成,储备池内部状态向量按式(1)进行更新。

z(n+1)=f(Winx(n)+Wresz(n)+Wbacky(n))

(1)

回声状态网络共有E个输出，通过输出连接权矩阵与网络的内部状态、输入以及输出反馈相连接，令

q(n)=(zT(n),x(n),y(n))T∈RF+D+E

(2)

因此，网络的输出可以按式(3)给出的输出方程计算

y(t+1)=Woutq(n)

(3)

式(3)中，Wout为输出连接权矩阵。回声状态网络中Win、Wres、Wback全部在网络初始化阶段产生，并在训练过程中保持不变，且网络最终只需训练Wout，克服了传统RNN网络需要求时序偏微分所导致的计算复杂、运算量大等问题，还有效地解决了前馈神经网络使用梯度下降法学习所导致的局部极小问题。

1.2回声状态网络的训练算法

回声状态网络具有大型动态储备池结构，因此网络有极强的构建复杂动力系统的能力。针对问题不同的需要，回声状态网络训练算法分为离线算法和在线算法两种。本文主要针对离线算法进行研究，下面将离线算法介绍如下。

第一步：构建一个储备池网络，并确保其符合“回声状态属性”。

首先应该确定内部连接权、输入连接权和反馈连接权矩阵。一旦这3个矩阵确定后，在整个网络训练进程中，这3个矩阵都会保持不变。

回声状态属性跟内部连接权矩阵Wres有关，然而直到现在仍没有系统的理论体系确保网络具有回声状态属性。但是经过反复研究实验，人们发现可以通过特定的方法产生内部连接权矩阵，进而提高网络具有回声状态属性的几率。具体方法如下：

1)随机产生一个稀疏矩阵W0，并确保这个矩阵所有权值的均值在0附近。

3)对W1进行一定的缩放，得到最后的内部连接权矩阵W，即W=αW1，在这里α<1。

第二步：将训练输入和输出样本输入加载到回声状态网络中。

训练输入、输出样本表示为(x(n),y(n),n=1,2,…,T)，当训练样本加载到网络中去后，储备池的动力特性被激发出来，储备池内部状态会依照式(1)不断变化。但在n=0时，网络各状态通常不是确定的，本文选取时z(0)=0,y(0)=0为初始状态。

第三步：淘汰储备池初始的状态记忆。

网络刚开始运转时，网络内部的状态可能并不是由网络的输入和输出引发的，所以n=1,2,…,T0这段时间内的网络状态记忆需要被淘汰掉，以便更好地反映输入和输出之间的关系。在T0之后，网络基本达到稳定状态，将网络输入、内部状态和输出以行向量形式(x(n),z(n),y(n))一并收集至矩阵H中。最终得到大小为(T-T0+1)×(D+F+E)的矩阵H;同时还需收集期望输出的sigmoid转置tanh-1d(n),以行向量的形式保存到矩阵G中，最终得到的矩阵G大小为(T-T0+1)×E。

第四步：计算输出连接权矩阵

在回声状态网络中，系统输出向量可以用储备池内部状态向量和输出连接权矩阵线性表示。网络对数据进行学习，通过训练最终使系统输出y(n)尽可能逼近期望输出d(n)，如式(4)所示。

(4)

将上述逼近问题转化为最小化问题，即求解最小化系统的均方误差：

(5)

该最优化问题最终转化成求解逆矩阵。如式(6)所示。

(Wout)T=H-1G

(6)

将矩阵H的逆与矩阵G相乘，得到一个大小为(D+E+F)×E的矩阵(Wout)T，其第i列包含网络中所有神经元节点至第i个输出单元的输出连接权值。

经过以上步骤即可完成对回声状态网络的训练。当利用回声状态网络进行预测时，先用训练数据对网络进行训练并将训练好的网络保存。进行预测时，将训练数据加载到训练好的网络中，得到预测结果。

1.3储备池的重要参数

储备池是回声状态网络最重要的组成部分，其参数选择对网络最终性能影响较大，需提前设定好。如何针对具体问题构建一个优良性能的储备池是学术界一直研究的问题，但到现在为止，学术界仍没有形成一个系统的方法。本文采用实验对比的方法对参数选取就行了研究，下面首先对储备池的一些关键参数作简要介绍。

1)储备池内部连接权矩阵谱半径SR

SR指的是储备池内部连接权矩阵Wres所有特征值中的绝对值的最大值，记为δmax。上文的训练算法已提到，当δmax<1时，网络才具有回声状态属性，确保网络能正常运行。

2)储备池神经元数量N

一般情况下，储备池神经元数量越多，网络对非线性系统的逼近能力越强。然而如果神经元数量过多，网络可能产生过拟合问题，进而导致网络泛化能力下降。

3)储备池输入单元尺度IS

IS指储备池的输入数据连接到储备池内部神经元之前需要相乘的一个系数。在处理实际问题中，样本数据往往不能直接作为输入信号直接加到储备池，需要通过IS对样本数据进行适当的缩放满足网络输入的需求。

4)储备池稀疏程度SD

储备池中神经元数量众多，关系复杂，然而并不是所有的神经元之间都有联系。SD指的就是相互之间有联系的神经元占总神经元数(N)的百分比。

2基于回声状态网络的跳频码预测方法

本文同时考虑到跳频码的混沌特性和回声状态网络良好的逼近非线性系统的能力，将回声状态网络引入到跳频码预测领域。通过上文的阐述可以知道，在利用回声状态网络对跳频码进行预测之前，有三个问题必须要考虑：第一是网络的输入输出数据如何选取；第二是储备池参数的确定，即构造适合于特定数据的储备池；第三是如何衡量预测性能的优劣。本节重点介绍网络输入输出数据选取、预测性能的衡量标准以及基于回声状态网络的跳频码预测算法流程。关于储备池参数选取的问题，因为一直没有系统的解决方法，本文在4.2节处会根据仿真数据进行实验比较，最终确定适合仿真数据的储备池参数。

2.1网络输入输出数据确定

(7)

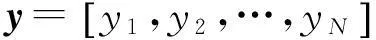
本文使用改进的C-C算法[7]对跳频码求解其最佳嵌入维数m和时间延迟τ,得到m和τ后，根据Takens嵌入定理，对整个跳频码进行相空间重构，即：

Gj=[yj,yj-τ,…,yj-(m-1)τ]

(8)

式(8)中，j=1,2,…,l,l=N-(m-1)τ。

根据Takens嵌入定理，如果选择了合适的嵌入维数m和时间延迟τ，重构相空间在嵌入空间的“轨线”就是微分同胚意义上的原系统的动力学等价。即存在映射F，使得

yj+h=F(Gj)=F(yj,yj-τ,…yj-(m-1)τ)

(9)

这里的映射关系F就反映了从Gj到yj+h的一个变化的过程。通过网络对数据的训练，最终确定映射关系F。本文对跳频码进行单步预测，则h=1，即网络训练的目标就是尽量去逼近Gj和yj+1之间的映射关系。

通过上文的描述可以知道，在网络训练时的输入数据为相空间重构后的跳频码矩阵，大小为1×m,输出数据为预测目标向量，大小为1×1。

2.2性能评估

本文中，使用预测准确率和有效预测率两个指标对跳频码序列的预测性能做评测。

预测准确率的均方根误差RMSE表达式如下：

(10)

在归一化的条件下，如果预测值和真实值偏差的绝对值在0.025以内，则认为对该点的预测是有效的，则有效预测率P[8]的表达式如下：

(11)

式(11)中，N为预测跳频码总点数，E为跳频码有效预测点数。

2.3基于回声状态网络的跳频码预测流程

1)确定网络的训练输入和输出矩阵。

通过2.1可以知道，根据具体的跳频码数据，利用C-C算法求得相应的最佳嵌入维数m和时间延迟τ，对跳频码进行相空间重构。跳频码训练样本长度以及预测步长需依照目标任务要求来确定，最终得到网络的输入和输出矩阵。

2)构建网络，确定储备池参数。

经过多次实验仿真，并将实验结果进行对比。在一定范围内，选取能产生最优储备池的4个参数，构建回声状态网络。

3)利用训练数据激活储备池，求取网络的输出连接权矩阵。

网络构建之后，将训练输入输出数据加载到网络中，激活储备池，并按照2.2节介绍的训练算法运转网络，收集相关数据，并最终求得输出连接权矩阵，保存训练完毕的网络。

4)测试跳频码的预测。

选取预测任务所要预测原点前的一段跳频码数据，按照流程1)的方法重新确定测试输入矩阵，并将数据加载到流程3)已训练好的网络中去，得到相应的预测结果。

具体预测流程框图如图2所示。

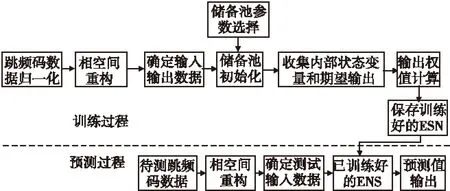
图2　基于回声状态网络的跳频码预测流程框图Fig.2　The prediction process of frequency hopping codebased on echo state network

3仿真实验和算法评估

本实验使用的计算机CPU主频4.6GHz，内存1.5G，仿真平台为MATLAB2009a。

3.1实验数据集

本文采用Logistic-Kent映射[9]、Lorenz系统中的x分量和MackeyGlass系统产生实验所需的跳频码。

3.1.1Logistic-Kent映射跳频码

Logistic-map表达式为：

x(k+1)=μx(k)(1-x(k))

(12)

式(12)中，3.75<μ≤4.0，0

Kent-map表达式为：

式(13)中，0<α<1，0≤y(l)≤1。

首先利用Logistic映射产生长度为X1的混沌序列Y1，接着再用Y1为Kent映射的初值产生X1个长度为X2的混沌序列，最后把X1个长度为X2的混沌序列连接在一起组成长度为X1×X2的混沌序列。通过级联混沌映射可以产生更长的混沌序列。

按照文献[9]方法产生码长为100×1 000的跳频码，取初始参数μ=4.0，α=0.2，x(0)=0.3。将所得跳频码序列进行归一化处理，为防止初始值过于接近，舍弃初始的2 000个点，然后再取4 000个点，其中3 000个点用于训练，后1 000个点用于测试。

通过C-C算法求的跳频码序列延迟时间τ=1，嵌入维数m=3。对上述数据进行相空间重构，得到如下规模的数据样本：训练输入矩阵大小为2 998×3，训练输出矩阵大小为2 998×1，测试输入矩阵大小为998×3，测试输出矩阵，即预测值矩阵大小为998×1。

3.1.2Lorenz系统跳频码

(14)

取参数σ=10，R=28，b=8/3，初始值向量为(-0.3,0.3,0.3)。用四阶Runge-Kutta算法，步长h=0.01，共求解x分量10 000点数据，并对其进行归一化处理，舍弃初始的2 000个点，然后再取1 000个点作为仿真数据，其中前500点用于训练，后500点用于测试。

通过C-C算法求得跳频码序列延迟时间τ=12，嵌入维数m=3。对上述数据进行相空间重构，得到如下规模的数据样本：训练输入矩阵大小为476×3，训练输出矩阵大小为476×1，测试输入矩阵大小为476×3，测试输出矩阵大小为476×1。

3.1.3Mackey Glass系统跳频码

(15)

取参数α=0.1，β=0.2，γ=10，初始值x(0)=1.2。用四阶Runge-Kutta算法，步长h=0.01，共求解x分量10 000点数据，并对其进行归一化处理，舍弃初始的2 000个点，然后再取1 000个点作为仿真数据，其中前500点用于训练，后500点用于测试。

通过C-C算法求得跳频码序列延迟时间τ=6，嵌入维数m=3。对上述数据进行相空间重构，得到如下规模的数据样本：训练输入矩阵大小为488×3，训练输出矩阵大小为488×1，测试输入矩阵大小为488×3，测试输出矩阵大小为488×1。

3.2储备池参数选取

回声状态网络性能的优劣跟参数选取直接相关，根据特定的数据样本挑选适合的储备池参数也一直是回声状态网络领域重难点问题。然而，人们到现在都未能研究出系统的理论分析解决这方面问题。本文以上述Lorenz系统的x分量为实验数据，研究储备池参数如何选取。

3.2.1神经元数量和谱半径对网络性能的影响

图3为SD=0.125，IS=0.1的条件下，不同神经元数量和谱半径下均方根误差比较。神经元数量的取值范围为[30,80]，步长为5，谱半径的取值范围为[0.1,0.9]，步长为0.1。从图中可以看出，当谱半径一定时，随着神经元数量增加，均方根误差基本上也在降低。所以神经元数量越多，预测准确度肯定会提高，然而这也会导致网络训练速度变慢，运行时间增长等问题，违背了回声状态网络设计的初衷，神经元数量可以进行折中选择。当神经元一定时，从图中可以看出均方根误差没有特别大的起伏，所以针对这组数据，谱半径的增减对预测误差影响不大。

图3　不同神经元数量和谱半径下预测性能的比较Fig.3　The comparison of prediction performance betweendifferent neuron and spectral radius value

3.2.2储备池稀疏程度和输入单元尺度对网络性能的影响

图4为SR=0.5，N=30的条件下，不同储备池稀疏程度和输入单元尺度下均方根误差比较。储备池单元尺度的取值范围为[0.1,0.9]，储备池稀疏度为[0.1,0.9]，两者步长都为0.1。从图中可以看出，当输入单元长度大于0.6后，无论稀疏度如何变化，均方根误差基本都处于一个较低的水平。所以针对该数据，输入单元尺度的取值只要大于0.6，稀疏度影响不大。

本文对Logistic-Kent映射和Mackey Glass系统跳频码作了同样的实验分析，在这里就不一一赘述。

图4　不同储备池稀疏程度和输入单元尺度下预测性能的比较Fig.4　The comparison of prediction performance betweendifferentsparsity degree and input scaling value

3.3实验结果和分析

根据上述实验结果，本文针对三种跳频码预测使用不同结构的回声状态网络。对于Logistic-Kent映射跳频码采用的网络参数为SR=0.05，N=500，SD=0.02，IS=0.1。对于Lorenz系统跳频码采用的网络参数为SR=0.9，N=80，SD=0.1，IS=0.7。对于Mackey-Glass系统跳频码采用的网络参数为SR=0.85，N=90，SD=0.1，IS=0.5。

图5至图7分别表示三种跳频码实际序列和预测序列，从图中可以看出，回声状态网络能够较好地预测出跳频码。

图5　Logistic-Kent原始序列和预测序列Fig.5　The prediction results of logistic-kent mappingfrequency hopping codes

图6　Lorenz原始序列和预测序列Fig.6　The prediction results of Lorenz system frequencyhopping codes

图7　Mackey-Glass原始序列和预测序列Fig.7　The prediction results of Mackey-Glass systemfrequency hopping codes

为了进一步凸显本文所构造回声状态网络模型的预测效果，从预测均方误差的角度做了对比分析，表1分别给出了不同方法RMSE预测对比结果。可见，回声状态网络的预测效果相比较更有优势，预测均方根误差最小。同时在有效预测率方面，Logistic-Kent映射跳频码有效预测率为99.2%，Lorenz系统和Mackey-Glass系统跳频码预有效预测率均为100%。

表1　三种跳频码的不同预测方法RMSE比较

跳频码序列预测不仅要注重准确度，对时效性也有极高的要求。本文实验中，将训练好的网络用于预测，Logistic-Kent映射跳频码平均每点预测耗时约为1.58 ms，Lorenz系统跳频码平均每点预测耗时约为0.72 ms，Mackey-Glass系统跳频码平均每点预测耗时约为0.66 ms。通过预测所耗时间可以看出，回声状态网络能满足500~1 000 h/s的中高速跳频码预测。

4结论

本文提出了回声状态网络混沌跳频码预测方法。该方法在对跳频码相空间重构的基础上，利用回声状态网络内部动态储备池的循环记忆功能，通过调整各权值矩阵的数值大小达到记忆数据的目的，解决了混沌跳频码预测问题。仿真实验表明该方法对Logistic-Kent映射、Lorenz系统和Mackey-Glass系统三种混沌跳频码都有较好的预测效果，并与其他方法的实验结果进行了比较，证明回声状态网络在混沌跳频码预测方面的可行性及优越性。本文还结合混沌跳频码预测问题，以具体仿真数据为切入口，讨论了储备池参数的选择问题。在下一步的研究中，将会把重点放在如何选取储备池参数上，寻求更一般的系统方法解决参数选择问题，以便进一步提高预测精度。

参考文献:

[1]郭双冰,肖先赐.几种跳频码的混沌动力学特性及预测分析[J].系统工程与电子技术,2000,22(12):29-32.

[2]党建亮,张家树.基于支持向量机的混沌跳频码预测[J]. 信号处理,2005,21(4A):122-125.

[3]Wang Wensheng, Yang Youlong,Li Yanying.Multi-step prediction of frequency hopping sequences based on Bayesian inference[C]//Information and Communications Technologies (IETICT 2013),Beijing:IET,2013:94-99.

[4]范越非,卢宏涛. 跳频码序列混沌预测的性能研究[J].计算机应用与软件,2011,28(8):83-86.

[5]WangYi, GuoWei.Frequency-hopping prediction based on the chaotic neural network[C]//Communication Technology, 2006. ICCT ′06.Guilin:ICCT,2006:1-4.

[6]HJaeger,The “ echo state” Approach to Analyzing and Training Recurrent Neural Networks[R].German:GMD German National Research Institute for Computer Science,2001.

[7]陆振波,蔡志明,姜可宇.基于改进的C-C方法的相空间重构参数选择[J].系统仿真学报, 2007, 19(11):2527-2530.

[8]霍思宇,混沌时间序列的预测方法研究[D].成都:电子科技大学,2010.

[9]李文华,王智顺,何振亚.用于跳频多址通信的混沌跳频码[J].通信学报,1996,17(6):12-16.

[10]党建亮,张家树.基于支持向量机的混沌跳频码预测[J].信号处理,2005,21(4A):122-125.

[11]张家树,郭双冰.混沌跳频通信的非线性自适应预测对抗[J].信号处理,2001,17(3):205-209.

[12]Takashi Kuremoto,Masanao Obayashi,Kunikazu Kobayashi,Takaomi Hirata,Shingo Mabu.Forecast Chaotic Time Series Data by DBNs[C]//Image and Signal Processing(CISP).Dalian:CISP,2014:1130-1135.

[13]Zhang Sichao,Liu Ping.Prediction of chaotic time series based on the relevance vector machine[C]//Advanced Computational Intelligence(ICACI). IEEE,2012:314-318.

[14]Gu Hong,Wang Hongwei.Fuzzy prediction of chaotic time series based on sigular value decomposition[J]. Applied Mathematics and Computation,2007,185(2):1171-1185.

摘要:针对现有跳频码预测方法存在的缺乏记忆能力、运算量大、训练过程复杂等问题，提出了基于回声状态网络的混沌跳频码预测方法。该方法在跳频码相空间重构的基础上，利用回声状态网络内部动态储备池的循环记忆功能，通过调整各权值矩阵的数值大小达到记忆数据的目的， 解决了跳频码预测的问题。仿真实验表明该方法对Logistic-Kent映射、Lorenz系统和Mackey-Glass系统三种混沌跳频码都有较好的预测效果，并与其他方法的实验结果进行了比较，证明回声状态网络在混沌跳频码预测方面的可行性及优越性。

关键词:跳频码预测；回声状态网络；混沌跳频码

Chaotic Frequency Hopping Code Prediction Method Based on Echo State NetworkLÜ Jijie1,2, YANG Junan1,2, GUI Yunchuan1,2

(1. Electronic Engineering Institute of PLA, Hefei 230037, China；

2.Key Laboratory of Electronic Restriction, Hefei 230037, China)

Abstract:As for the problem of frequency hopping prediction such as the incapability of memorization, vast computation and complex training procedure, a new method for chaotic frequency hopping codes prediction based on the echo state network was proposed. The method, which was under the premise of the phase space reconstruction, solved the problem by taking the advantage of the cyclic memory function of dynamic reservoir and adjusting the numerical size of each weight matrix to achieve the purpose of memorizing data. The simulation experiments showed that the method achieved great prediction performance for the three chaotic frequency hopping codes generated by Logistic-Kent mapping, Lorenz and Mackey-Glass system respectively.

Key words:frequency hopping code prediction;echo state network; chaotic frequency hopping code

中图分类号:TN914.4

文献标志码:A

文章编号：1008-1194(2015)06-0092-07

作者简介:吕季杰(1991—)，男，安徽郎溪人，硕士研究生，研究方向：信号处理，混沌预测。E-mail:Ljj615315@163.com。

*收稿日期:2015-05-26