基于中心线预估计的蛇形机动弹道识别算法

郑昌艳，梅　卫，刘　恒, 王　刚

(解放军军械工程学院，河北 石家庄　050003)



基于中心线预估计的蛇形机动弹道识别算法

郑昌艳，梅卫，刘恒, 王刚

(解放军军械工程学院，河北 石家庄050003)

0引言

对于新型高速无人机、再入飞行器、战斗机及反舰导弹等，蛇形机动是一种成熟应用的规避技术。该机动很大程度上增加了雷达的跟踪误差、高炮前置计算误差和导弹追踪的飞行过载，对防御系统构成了巨大威胁。因此拦截蛇形机动目标是现代防御拦截系统研究的热点，也是未来拦截技术发展必须解决的关键问题之一[1]。

基于现有的目标跟踪技术，高炮集火射击很难完成对高速机动目标的打击，空域窗射击体制[2]通过合理预设弹丸散布中心，扩大有效毁伤目标区域，能有效提高高炮打击效能。对于蛇形机动目标，空域窗射击参数需在识别蛇形机动模式基础上，根据目标蛇形机动中心线、机动幅度等进行弹丸散布设置;导弹武器系统采用微波、激光、红外或者光电复合制导技术，在目标做蛇形机动时会追随其做高速机动，严重影响其自身系统的稳定性与可靠性。在对目标跟踪基础上，若能判别其是蛇形机动模式，沿着蛇形机动中心线进行追踪，对提高导弹性能的稳定性具有重要意义。

目前识别目标蛇形机动的方法主要是通过提取目标轨迹运动参数特征。文献[3]通过提取目标位置变化率特征实现对蛇形机动的识别，但文献[3]论述的蛇形机动特征只在蛇形机动沿着特定方向成立，且对噪声敏感，鲁棒性较差。文献[4]将图像处理中边缘拐点检测方法[5]应用到运动模式分段处理上，之后运用运动学分析法识别目标运动模式，但文献[4]将重点放在弹道分段方法上，对蛇形机动模式识别论述较模糊，且未涉及到中心线及幅度估计问题。本文针对上述问题，提出了基于中心线预估计的蛇形机动弹道识别算法。

1巡航导弹运动模式及蛇形机动仿真参数分析

1.1巡航导弹运动模式分析

巡航导弹由于其飞行高度低，雷达反射截面积小，突防能力强，射程远，精度高等突出特点，备受各国军队青睐，是防空武器系统的主要作战对象之一。其经典弹道主要分为两个阶段[6]，如图1所示。

1)平飞阶段：导弹从不同发射平台发射后，加速爬升到一定高度助推器脱落，再迅速降低高度(根据不同地形段在15～100 m之间)进入巡航飞行。这个阶段内，巡航导弹一般采用匀速直线运动模式，在飞行后期做蛇形机动以躲避防空武器系的拦截，速度为0.7～0.9Ma。

2)攻击阶段：导弹先跃升至一定高度，再进行俯冲攻击。该方式可有效逃避火炮攻击，是多种导弹攻击目标的通用形式。

图1　典型的巡航导弹弹道Fig.1　Typical cruise missile trace

1.2 蛇形机动仿真参数分析

作战飞机受本身机动性能制约，且考虑人的操控和飞行转弯时人和飞机所能承受的过载，飞机进行蛇形机动时，周期一般在5～10 s，机动幅度50～100 m。而导弹的蛇形机动一般采用过载控制方案，通过舵偏指令控制导弹飞行，主要体现为航向角和水平面法相加速的的反复变化。其机动性能高，承受过载能力大，蛇形机动周期一般在3～5 s,机动幅度30～200 m[7]。本文重点研究平飞阶段巡航导弹的蛇形机动模式识别。

飞行航迹模型参考坐标系选用WGS84大地坐标系(B,L,H)和高斯投影坐标(X,Y,Z(H))。目标航向(θ)(北偏东度数)是以正北为0°沿顺时针方向度量的角度。模型处理约定：水平面上，正北方向为X轴正向，正东方向为Y轴；垂直于水平面为Z(H)轴方向，向上为正，向下为负[8]。

设置量测角噪声标准差为1 mil,量测距离噪声标准差为5 m,采样频率50 Hz,采用卡尔曼滤波跟踪。

2基于中心线预估计的蛇形机动模式识别及幅度估计

进行蛇形机动弹道识别时，包括蛇形机动模式识别和幅度估计两部分内容。机动幅度的估计和模式识别并非完全独立的过程，在模式识别中找的拐点和周期性零点等特征，同样也是估计机动幅度的关键。

本文先阐述基于中心线预估计的蛇形机动模式识别及幅度估计算法的流程和思想，再在第2章的各小节中给出了各个步骤的具体算法。

算法具体流程如下：

步骤1：检测拐点

先判断目标航迹由直线运动模式转为机动模式(蛇形机动，转弯机动，航道偏离等)的时刻点，该时刻称为运动模式转换点，即拐点。

步骤2：拟合中心线

拟合出目标在拐点后一段时间t内飞行大致所沿的航向线，称为预估中心线。

步骤3：寻找零点、周期性零点

寻找上述时间t内与预估计中心线无限接近的航迹点，称为零点。由于航迹数据是离散数据，故会检测到多个零点。与其他机动模式不同的是，蛇形机动围绕中心线上下波动，因此若时间t大于一个蛇形机动周期时间，那么必然存在大于等于3个“零点簇”，“零点簇”中心称为周期性零点。因此可通过周期性零点个数排除非蛇形机动模式。图2(a),(b)分别是求解的转弯机动模式和蛇形机动模式的周期性零点个数。

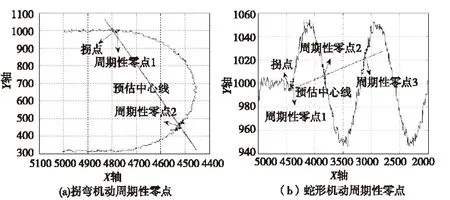
图2　不同机动模式的周期性零点图Fig 2 Cyclical zero-points on different modes

步骤4：纠正中心线及估计幅度

由于预估中心线与真实机动中心线存在偏差，需进行中心线纠正,再进行幅度估计。具体的算法在下一章节中给出。

步骤2到步骤4得到的航迹特征点均是基于预估中心线计算得出，故算法命名为基于中心线预估计的蛇形机动弹道识别。

整个算法流程如图3所示。

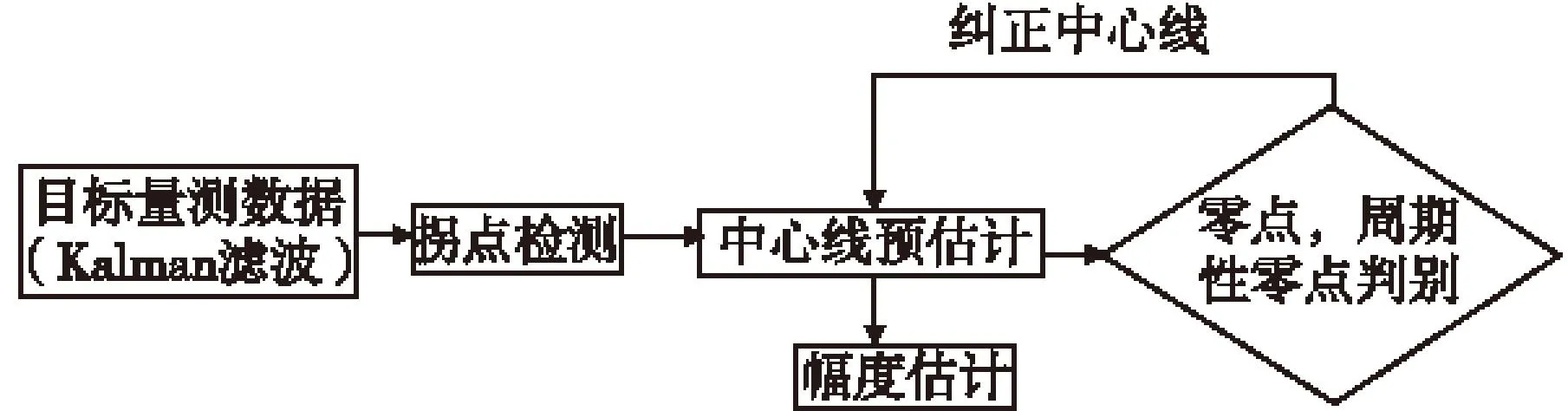
图3　算法流程图Fig.3　Algorithm Flow chart

倒逼法寻求拐点原理如下所述。假设P1,…,Ps,…,Pk,…,Pk+s-1是目标航路投影线上的k+s-1个采样点(如图4所示)，利用最小二乘对P1~Pk，k个点进行直线拟合，得到直线L1,计算航向角θ1。保持拟合点个数k不变不断移动初始点得到不同航向角θ2,θ3,…,θs,…。不断取间隔为s的航向角做差，即将点Ps~Pk+s-1和点P1~Pk分别拟合成的Ls,L1直线的航向角做差，当角度差Δθ达到一定阈值，则判断Ls起始点Ps与L1的末端点Pk的中点为拐点Pm。该方法通过选取适当拟合点个数k能充分展示一小段时间范围内航迹的大致运动方向。由于噪声存在，k过小会导致拟合航向角剧烈变化，忽略了整体运动趋势；k过大会忽略运动过程中的细节变化，且造成对拐点判断的迟滞。实验证明，选取目标0.5 s的时间范围进行最小二乘直线拟合效果较好，则

k=0.5f

(1)

式(1)中，f为采样频率。

图4　拟合直线倒逼拐点检测法Fig.4　Switch point detection based ontwo-fitting-line force

间隔s的选取，过小则航向角度差普遍过小，不利于判别；过大，则易造成角度差普遍过大也不利于判别，并且会造成拐点判断前置。实验得出，s选为k/2较好。

选取前段直线末点后后端直线的起始点两点中点，能更准确地定位拐点。实验得出Δθ最佳阈值为5°。

实验证明，拟合直线倒逼法寻找运动模式转换点具有很强的抗噪性与通用性。图5(a),(b)分别为累加弦长法和拟合直线倒逼法寻找到的拐点。

图5　拐点检测对比图Fig.5　Comparison Chart on switch point detection

2.2中心线预估计

检测到拐点(x0,y0)后，假定拐点后t时间范围内航迹中心线为l1:y=kx+b，拐点在直线上，则b=y0-kx0。计算t时间范围内航迹到该直线的距离和，可得到关于k的函数。通过寻找最小距离，可确定k的大小，即可得到中心线方程。时间t越长越对机动大致飞行方向估计越有利，但影响判别时效。同时由于本文是利用周期性零点个数进行判别，故t的选取一定大于其最大蛇形机动周期时间，综合考虑本文选择t为5.5 s。

2.3零点及周期性零点寻找

计算t时间范围内各航迹到l1的距离，若距离小于一定值阈值Δd，判定该点为零点。Δd过大，则零点判断过多，Δd过小，则可能漏掉零点。实验证明，Δd为10 m较合适。

找到零点后，需对“零点簇”进行“聚类”。将时间间隔很小的零点，归为一类，取每个类别中所有零点时刻的中心时刻，为周期性零点。若周期性零点数量大于等于3，即知其围绕中心线上下波动，判定为蛇形机动。

2.4中心线纠正及幅度估计

2.2节中对中心线进行了粗略估计，当判别模式为蛇形机动后，可利用上述得到的特征点进行中心线纠正。

分别取相邻的周期性零点之间的航迹点，寻找它们到预估中心线距离的最大值点，将找到的相邻最大值点取中点，判定为纠正的中心线上一点。图6为展示了预估中心线和纠正的中心线。

再计算相邻周期性零点间到纠正的中心线的最大距离值，取平均得到幅度估计值。

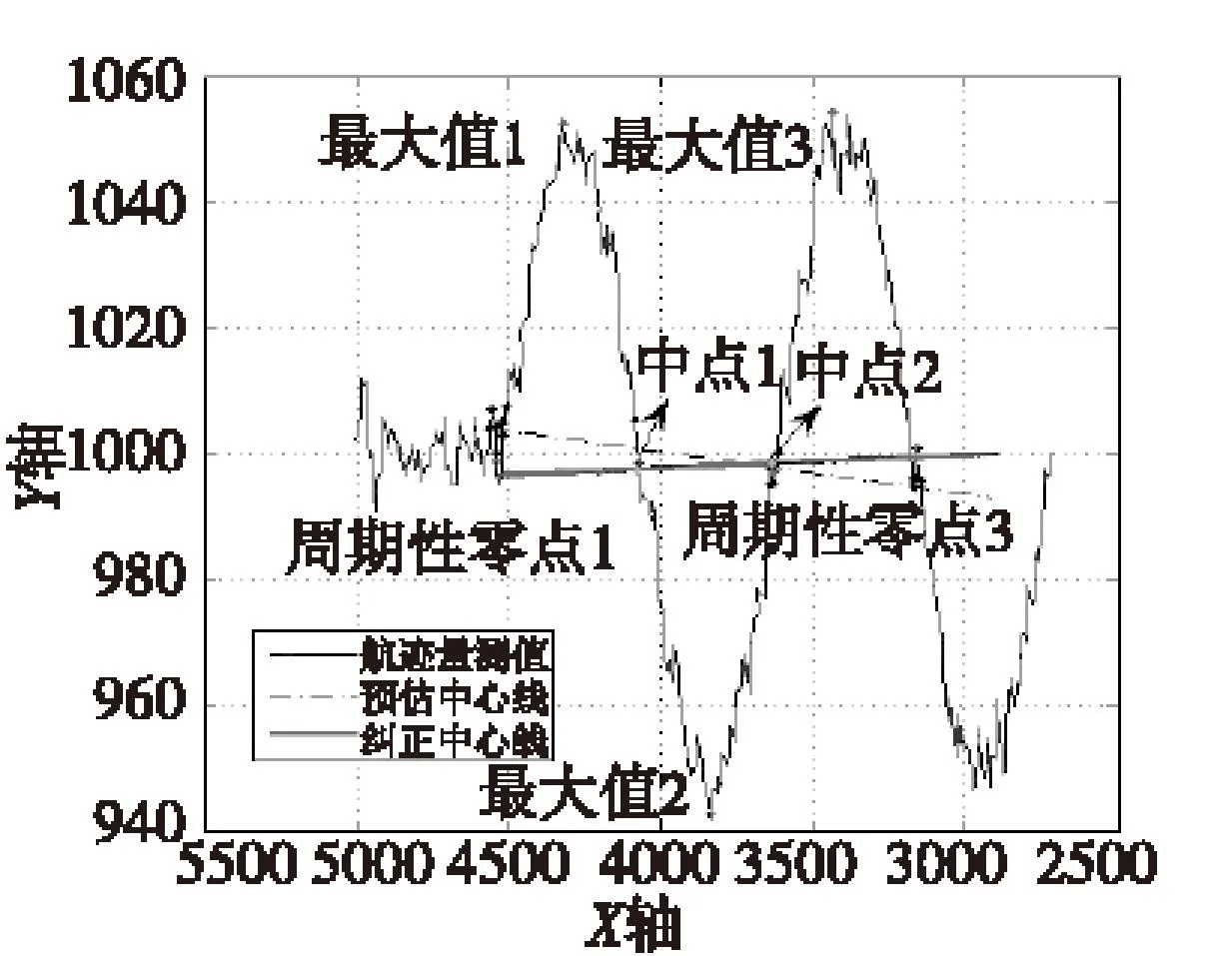
图6　预估中心线和纠正中心线Fig.6　Predictional centre-line and corrected centre-line

3实验验证

采用蒙特卡洛仿真方法，对所提算法的有效性和可行性进行验证。

3.1蛇形机动模式识别率验证

仿真条件：目标航迹分为两段，前一段做直线运动，后一段做蛇形机动。

1)测试不同速度下的蛇形机动识别率。

速度在200~340 m/s之间，速度间隔1 m/s,每个速度进行100次仿真实验，得出不同速度下的识别率如图7所示。

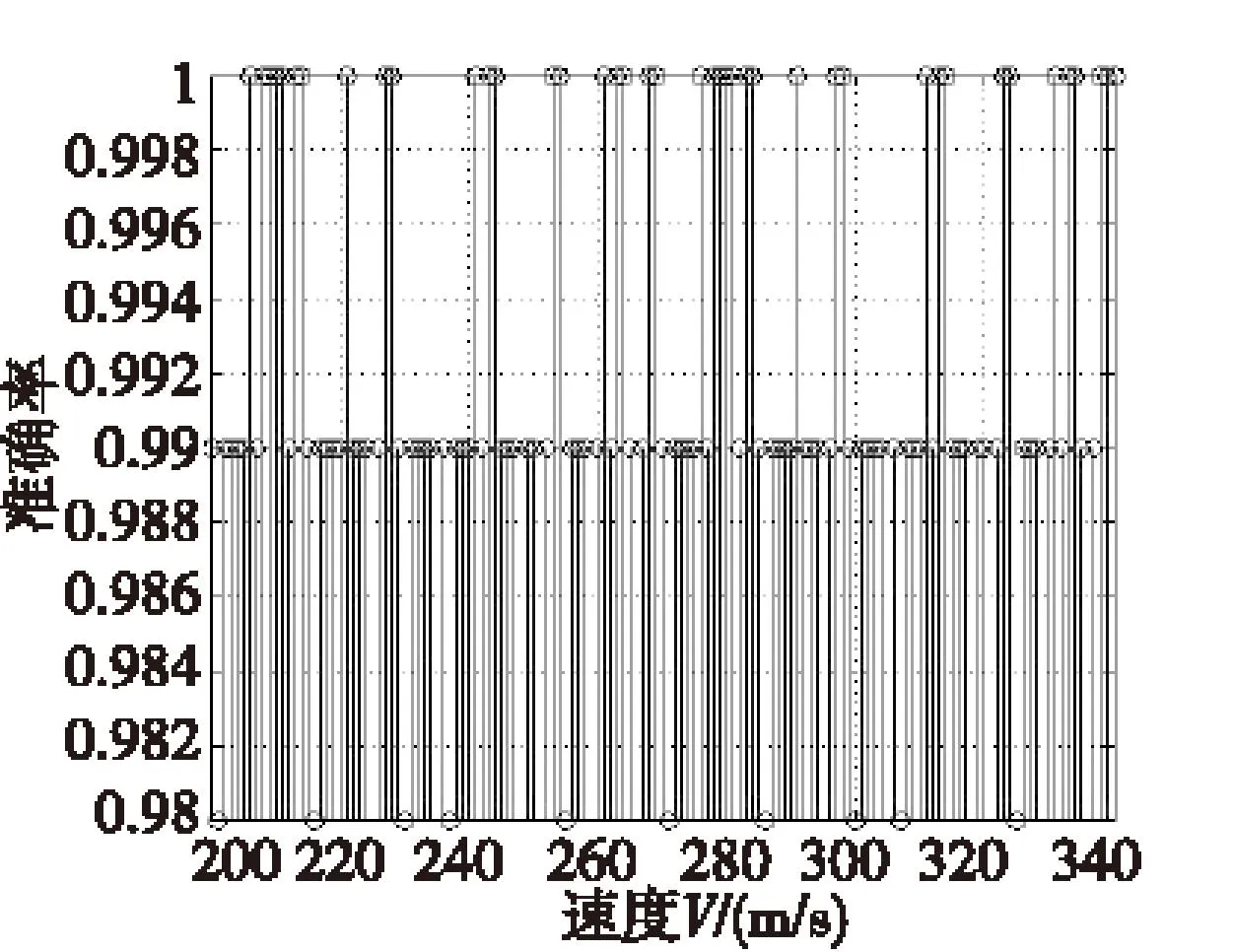
图7　不同机动速度下的模式识别率Fig.7　Rate of pattern recognition under different velocity

由图7可看出，在不同速度下识别率保持在98%~100%之间，差别不大，故算法识别率与速度无关。

2)测试不同速度、不同机动幅度、不同机动周期下的蛇形机动识别率。

速度在200~340 m/s之间，机动幅度在30~200 m，机动周期在3~5 s之间随机取值，进行1 000次仿真实验，识别率如图8所示的。

标志数=1表示识别出蛇形机动模式，标志数=0表示未识别出蛇形机动模式。经统计，1 000次仿真中有16次未识别出，识别率为(1 000-16)/1 000×100%=98.4%，相比于文献[3]的97.4%精度提高了1%。

识别率未达到100%是由于初始位置过远，kalman滤波得到的目标位置误差大，而蛇形机动幅度过小，机动幅度淹没在噪声中不明显导致的。目标位置误差越小，识别率越高。

3)与文献[3]识别蛇形机动方法进行比较实验。

本文对文献[3]提出的方法进行了仿真实验，在量测角噪声标准差为1 mil,量测距离噪声标准差为5 m的状态下进行测试，其识别率为97%与文章中所述相符。当加大噪声，量测距离噪声标准差为10 m时，测试结果如图9所示。

500次的仿真实验中有36次未识别出，识别率为92.8%，而本文所提出的算法在相同的噪声情况下识别率为97.8%。

文献[3]中在判断时考虑了拟合直线的斜率大小，在噪声较大情况下航迹数据波动大，导致识别性能降低。本文判断的是与拟合直线接近的特征点个数，相比之下抗噪性更强。

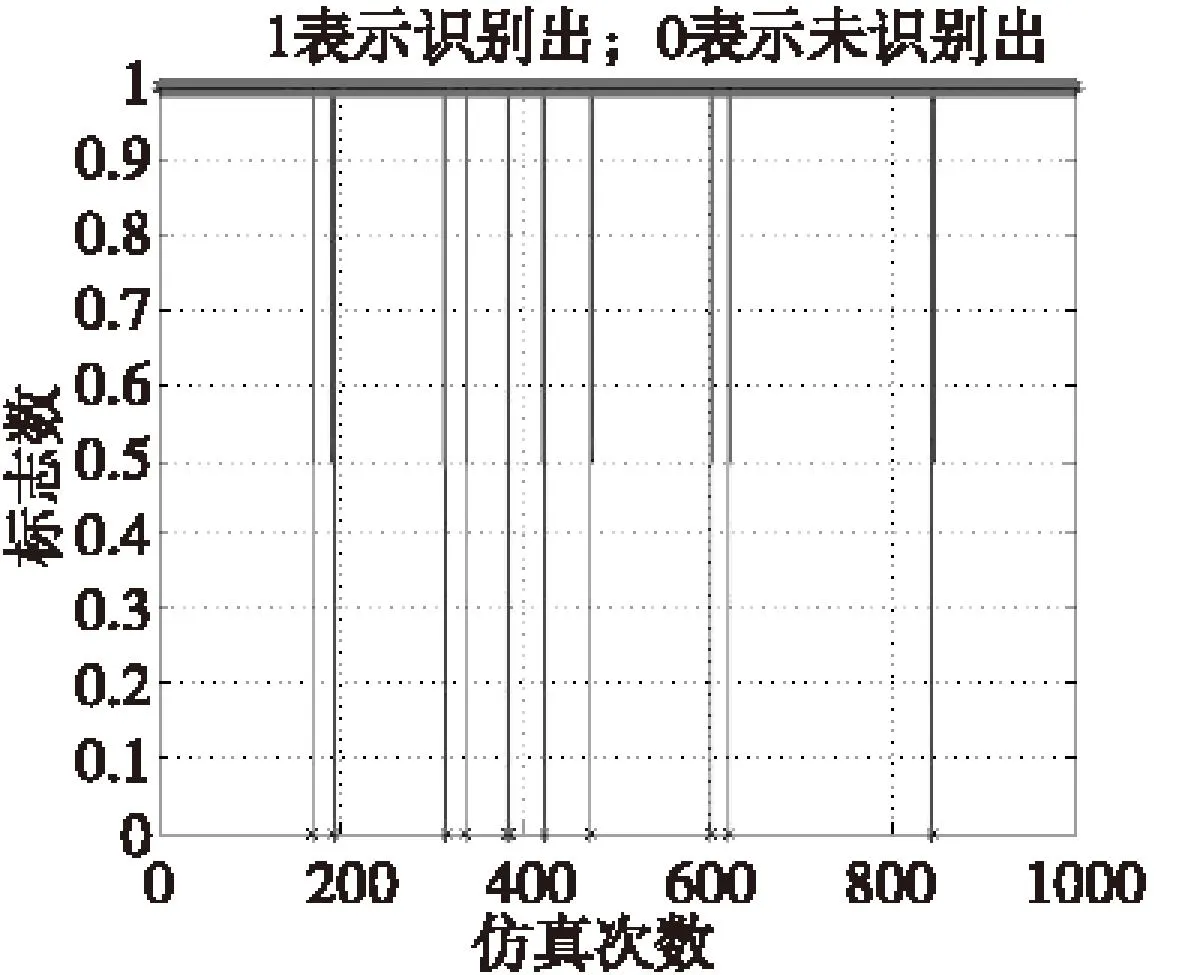
图8　模式识别率Fig.8　Rate of pattern recognition

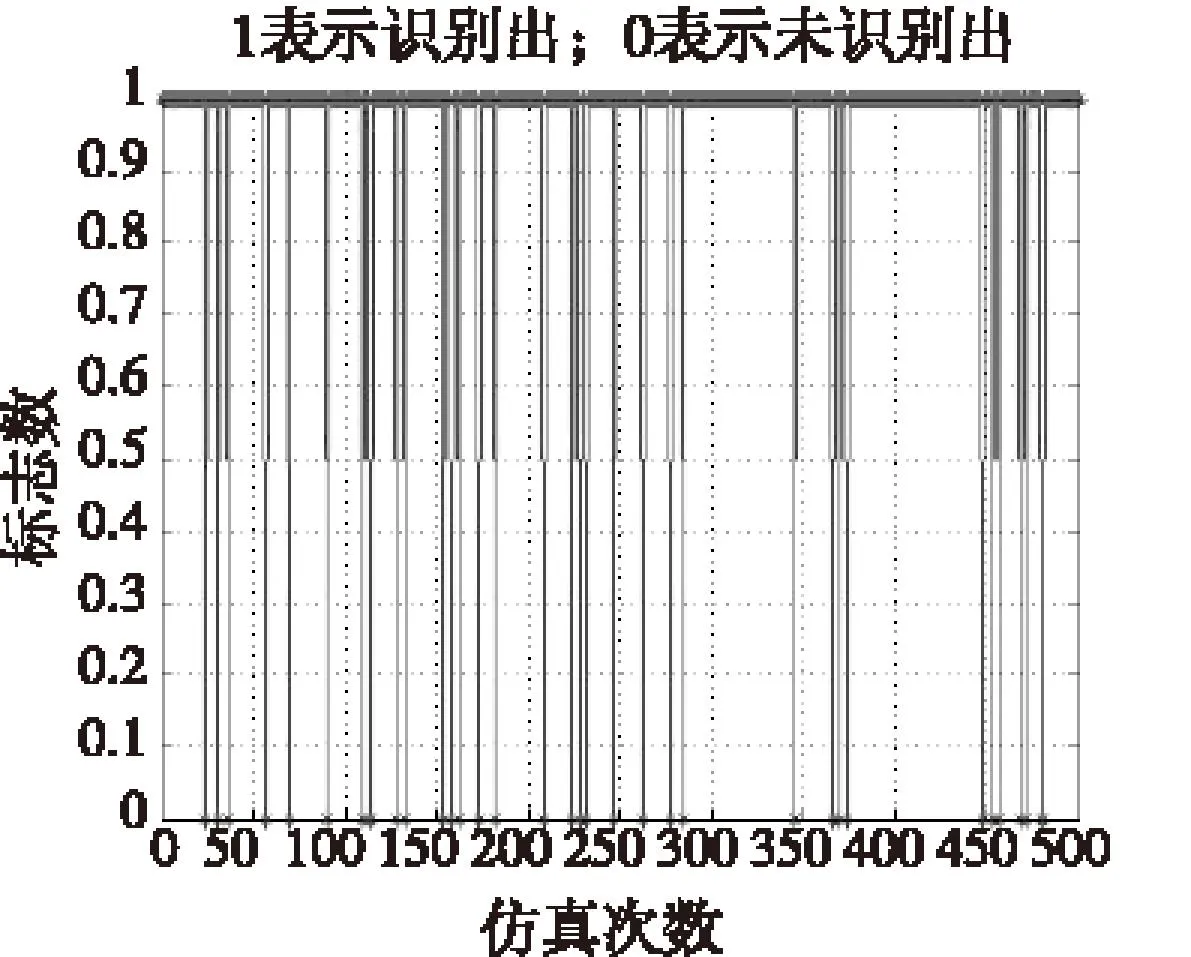
图9　基于位置变化率的模式识别率Fig.9　Rate of pattern recognitionbased on position slope

3.2蛇形机动幅度精度仿真

仿真条件：蛇形机动幅度真值为50 m(仅在Y轴)，蒙特卡洛仿真次数500次。

仿真结果如图10所示。由于对中心线估计有偏差，幅度估计值比真实值偏大。幅度估计值与真值的相对误差均值为6%，估计的幅度取得了较好效果，基本达到预期要求。

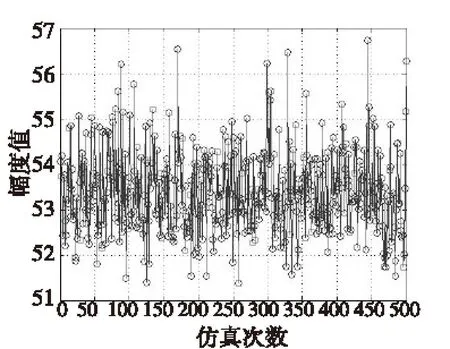
图10　幅度估计值Fig.10　Estimation range

4结论

本文提出了基于中心线预估计的蛇形机动模式识别和幅度估计算法。该算法先采用拟合直线倒逼法检测运动模式拐点；再对模式切换后的飞行航迹进行大致的方向拟合，结合周期性零点个数和航迹在中心线波动相差范围进行机动模式识别；进而利用相邻周期性零点间距离中心线最大值点进行幅度估计。航路仿真表明，该算法的模式识别率可达到98.4%，提高了现有的蛇形机动识别精度。幅度估计值与真值的相对误差均值为6%，是有效的。后续研究主要是提高对蛇形机动中心线和幅度估计精度，使防御系统对目标蛇形机动拦截打击更精确。

参考文献:

[1]刁兆师,李海田,单家元.拦截蛇形机动目标考虑自动驾驶仪动态特性的最优制导律[J].北京理工大学学报，2013,33(3):229-234.

[2]胡金春.未来空域窗体制下的火力控制理论[D].南京:解放军理工大学，1998.

[3]刘恒,梅卫,单甘霖.基于位置变化率的蛇形机动弹道识别[J].探测与控制学报，2013, 35(3):37-40.

[4]韩萍,于俊伟.基于运动学分析的反舰导弹弹道识别[J]. 电光与控制，2011,18(9):31-34.

[5] Mohannad Awrangjeb,Guojun Lu,Clive S.Fraser etal.A Fast Corner Detector Based on the Chord-to-Point Distance Accumulation Technique[C]//Digital Image Computing:Techniques and Applications Conference.Australia:2009:519-525.

[6]张宏.巡航导弹的作战使用特点及对抗途径[J].舰船电子对抗，2009,32(4):19-24.

[7]冯元伟,夏小华,吴艳征.导弹两种蛇形机动对反导舰炮突防效果比较[J].火力与指挥控制，2011,36(8):107-108.

[8]苏春梅,冯朝阳,王力军.通用飞机航迹生成技术[J].兵工自动化，2010,29(12):20-25.

摘要:针对现有蛇形机动识别算法鲁棒性差，识别精度不高的问题，提出了基于中心线预估计的蛇形机动模式识别和幅度估计算法。该算法先检测运动模式切换点即拐点，采用拟合直线倒逼法解决了当前航迹拐点检测算法抗噪性差的问题；再对模式切换后的飞行航迹进行大致的方向拟合，结合周期性零点个数和航迹在中心线波动相差范围进行机动模式识别；进而利用相邻周期性零点间距离中心线最大值点进行幅度估计。仿真结果表明：该算法的模式识别率可达到98.4%，幅度估计值与真值的相对误差均值为6%。

关键词:目标识别；拐点检测；蛇形机动;中心线预估计；幅度估计

Zigzag Maneuver Trajectory Recognition Based on Centre-Line PredictionZHENG Chang Yan, MEI Wei, LIU Heng,WANG Gang

(Ordnance Engineering College of PLA ,Shijiazhuang 050003, China)

Abstract:In order to improve the interception ability of anti-aircraft system, aiming at the robustness and accuracy shortages of the existing algorithm for pattern recognition of zigzag maneuver, an algorithm of pattern recognition and range estimation for zigzag maneuver based on centre-line prediction was proposed in this paper. This method used the two-fitting-line force method, which improved the anti-noise ability of existing algorithm, detected the track mode switch point, and then general track direction was estimated after the switch point. Movement pattern was recognized through the number of cyclical zero-points and the range of the distance to the centre-line, moreover, its range was estimated by the biggest distance to the centre-line between cyclical zero-points. Simulation results showed that the pattern recognition ratio was 98.4%, comparative error between the calculation results and true value was 6%.

Key words:target recognition; track mode switch point; zigzag maneuver, centre-line prediction; range estimation

中图分类号:TP271

文献标志码:A

文章编号：1008-1194(2015)06-0061-05

作者简介:郑昌艳(1990—),女，江苏南京人，硕士研究生，研究方向：火力与指挥控制。E-mail:echoaimaomao@163.com。

基金项目:国防“十二五”预研项目资助(40405070102)

*收稿日期:2015-06-11