基于边界元的舰船水下静态电场推算方法

何　芳，王向军，高俊吉

(海军工程大学电气工程学院,湖北 武汉　430033)



基于边界元的舰船水下静态电场推算方法

何芳，王向军，高俊吉

(海军工程大学电气工程学院,湖北 武汉430033)

0引言

在舰船静态电场建模方面，目前主要有边界元法(BEM)[1-2]、有限元法(FEM)[3-4]、等效电偶极子法[5-6]，舰船电场的深度换算是电场建模的重要研究内容。舰船静态电场的深度换算目前国外未见有报道，国内可见报道很少，可查资料显示只有海军工程大学在该方面做了初步工作，主要采用点电源法[7-8]、电偶极子法[9-11]、平面迭代法[12]进行深度换算。文献[8]采用点电源产生的静电场模拟船舶，利用泰勒展开式的收敛半径对场源的个数和位置进行了准确的计算，建立了基于点电源的静态模型，再反演得到模拟源的模型，最后利用此模型计算目标深度上的静电场。此方法对建模要求很高，模型的准确度对换算结果影响较大，计算过程较为复杂。文献[9-11]主要是基于电偶极子进行无限大平面的深度换算，解决了电场某分量向下进行较大深度自换算和互换算的问题，文献[12]利用微分原理，根据静态电场各分量与其垂直分量的偏导数关系，建立各无限大平面之间的数学关系，采用迭代算法解决海水中静态电场向较浅深度换算问题。但是基于无限大平面理论的深度换算在转化为数值积分后，对换算深度、测量点距及测量平面尺寸都有要求，若换算深度小于测量点距或测量平面尺寸接近换算深度时都会产生较大误差，同时在工程实际应用中，无法在无限大平面上测量，只能在有限平面内取值，造成了换算精度的下降，不利用指导工程实践。本文针对此问题，提出了基于边界元的舰船水下静态电场推算方法。

1水下静态电场的边界元模型

建立水下静态电场边界元模型的思路是：先建立半无限域任意形状的闭合曲面边界面积分模型；然后通过对边界面进行正方形面元剖分，将边界积分方程离散为代数方程组，解出边界源点近似解，并对边界奇异9+++点进行数值处理；最后根据域内场点与边界源点近似解的关系式，求解半无限域内的静态电场分布。

1.1任意形状的闭合曲面边界面积分模型

舰船静态电场是由海水中的稳恒电荷分布产生的，基于媒质内部均匀且各向同性的假设,稳恒电荷只分布在空气和海水、海水和舰船以及海水和海床的分界面上, 海水内部无净电荷存在，电荷面密度与分界面两边媒质的电容率有关。若在近场区取一任意形状闭合曲面，海水无限远处边界面视为S∞,S0-S∞构成一无限域V,半无限域V的内边界面S0的外法线方向指向无限域内部，如图1所示。半无限域V内的静态电场则满足Laplace方程。

(1)

设边界面S0上有一源点M0,M为无限域V中的任意一场点，r为源点到场点的距离。半无限域内场值与内边界面S0上函数值关系，可以通过Green第三公式[13]推导得出：

(2)

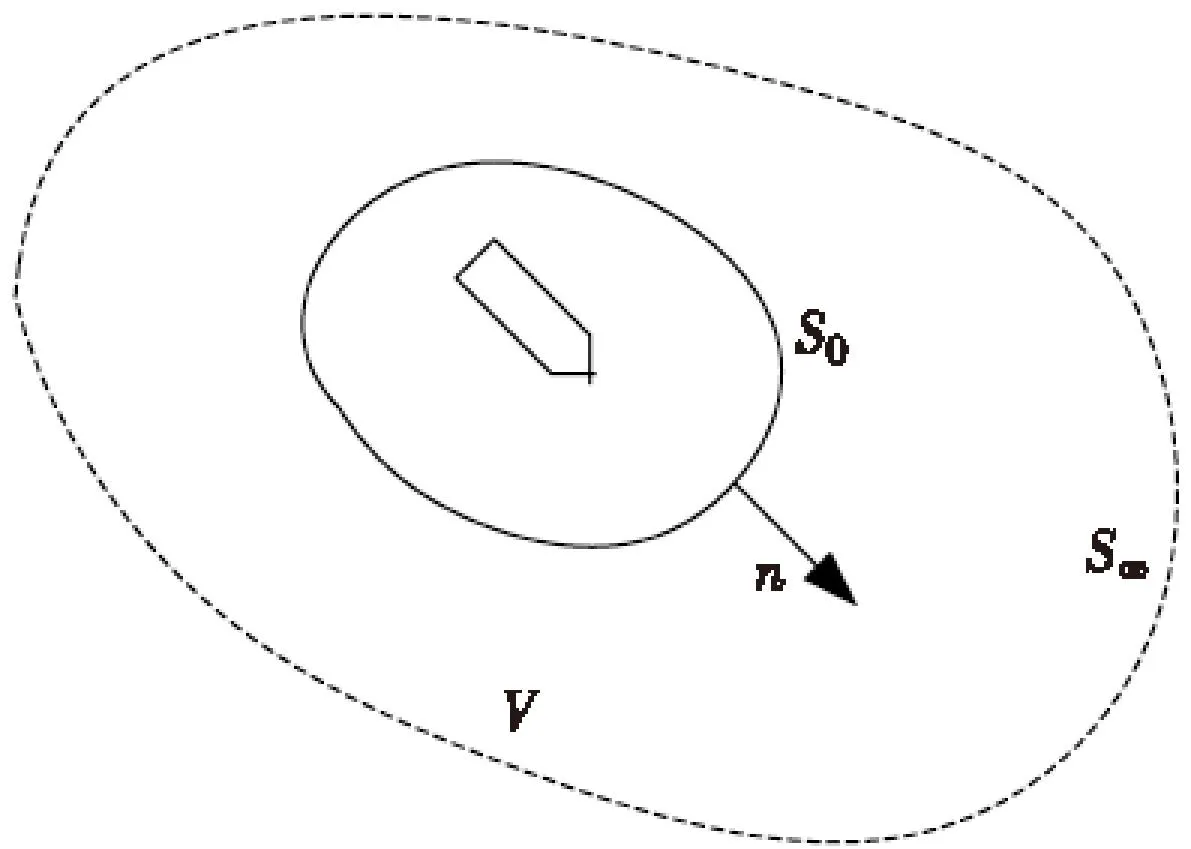
图1　舰船水下电场半无限区域平面图Fig.1　Schematic of vessel electric field in the semiinfinite domain

1.2边界积分方程离散及奇异点处理

设边界面S0上的有限测量点为M0，根据Green第二公式[13]推导出边界积分公式为：

2πu(M0)=

(3)

(4)

式中，i=1,2,…,k。ri,j为面积元dSi的中心与面积元dSj的中心之间的距离。

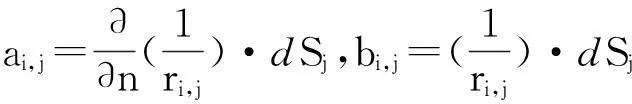
(5)

当i=j时 ，场点和源点在同一积分面元上，边界面积分出现奇异点。用正方形小面元(面元边长为a)，正方形面元坐标设置如图2所示，计算得

(6)

图2　正方形面元的坐标设置Fig.2　setting of coordinate in a element

用矩阵方程描述即为Ak×kU1×k=Bk×k,系数矩阵A，B均为k×k的满秩方阵，U1×k即边界面上的整个电场分布。为了便于说明，在笛卡儿坐标系下对代数方程组系数A，B进行确定。以平行于潜艇纵向方向由舰尾向舰首为X轴正方向，以平行于潜艇横向方向由左舷向右舷为Y轴正方向，以垂直于水面指向地心为Z轴正方向。以潜艇为中心取一长方体表面作为边界闭合面，六个面上的法线方向都指向长方体内部，如图3所示。

图3　长方体边界面及坐标系Fig.3　Boundary surface and its coordinate system

ri,j为面积元dSi的中心与面积元dSj的中心之间的距离：

(7)

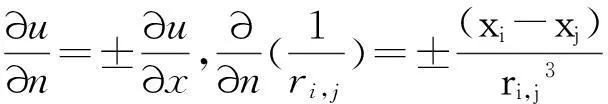
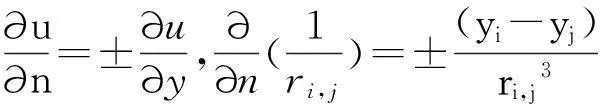
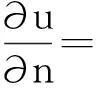
只要边界面的形状和具体剖分方法确定了，矩阵方程Ak×k=Bk×k的系数矩阵A，B就能惟一确定。解此方程组,可以直接计算出U1×k，得到边界面上各面元中心处的电势u，即边界面上源点的近似解。

1.3基于边界元法的水下静态电场分布

将边界面上各面元中心处的电势代入式(2)，得到半无限场域内电场强度的函数解析解。

(8)

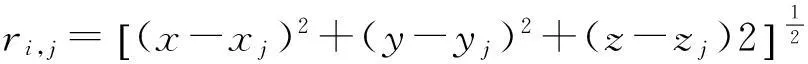
(9)

2基于边界元的舰船水下静态电场推算方法

为了接近实际情况(方便潜艇通过)，不考虑边界面S1，S2两个侧面的电场分布，验证采用长方体四个面近似闭合曲面的水下静态电场边界元模型是否准确可靠，采用MATLAB进行仿真。将一单位电偶极子放置于水深5 m处，设计边界面为一长方体外表面，如图3所示，长宽高分别为x∈(-6,6)m,y∈(-1.5,1.5)m,z∈(-1.5,1.5)m。忽略长方体S1，S2两个侧面，将其余四个侧面每个面都剖分为648个正方形面元，共计剖分2 592个面元，每个面元的中心点电场强度作为整个面元电场强度的平均值。 应用式(9)，换算得到长方体表面积外的半无限区域内任意位置的电场三分量，以此作为水下静态电场边界元模型。

2.1利用边界元模型外推直线处电场

利用水下静态电场边界元模型外推直线z=20 m,y=0,x∈(-50,50) m处的电场三分量，以及电偶极子在相同位置直接产生的电场三分量对照情况如图4所示，与文献[5]的电场分布解析表达式仿真结果(理论值)完全吻合。

2.2利用边界元模型外推平面处电场

利用水下静态电场边界元模型外推平面z=20 m,y∈(-50,50) m,x∈(-50,50) m处的电场三分量，如图5所示。仿真结果与文献[9]采用无限大平面法换算得到的相同平面处电场三分量在数量级上是完全吻合的。

仿真结果证明了采用长方体四个面近似闭合曲面的边界元模型是可行的，且验证了基于该边界元模型的水下静态电场推算方法的正确性和可靠性。

图4　电场三分量仿真推算值和理论值对比图Fig.4　The results of the calculated and the theoretical for the components of electric field intensity

图5　边界元换算平面电场分布图Fig.5　Result of BEM on plane

3实验验证

为了验证基于边界元水下静态电场推算方法的有效性及换算精度，在实验室采用潜艇模型进行实验验证。

3.1实验条件和实验步骤

实验硬件设施包括无磁性实验水池、实验潜艇模型、电场三分量传感器及矩形测量架。无磁性实验水池，尺寸为8m×5m×1.5m,水深0.8m，将工业用盐倒入池水中，充分溶解并混合均匀，模拟淡盐水，测得所配制的海水电导率为3.96S/m。潜艇模型长1.5m,宽0.13m，高0.15m，按实艇缩小比例1∶100制得。艇模船壳铁制，螺旋桨青铜制，船模的不同金属结构在模拟淡盐水中因电化学作用产生腐蚀电流，为防止船壳腐蚀，艇模上装载了阴极保护系统(ICCP)，而防腐系统的开启也会在模拟淡盐水中产生电流。这些腐蚀和防腐电流在模拟海水(池水)中形成了静电场。

矩形测量架宽0.4m,高0.4m。完全置于水中固定，测量架每条边上均匀布放3个电场三分量传感器。

实验步骤如下：

1)将艇模移至距测量架较远处，电场三分量传感器采集背景电场。

2)以测量架为中心建立笛卡儿坐标系，潜艇沿X轴匀速穿过测量架，如图6所示(潜艇由纸内向纸面运动)，电场三分量传感器可以采集到艇模在各个位置时的电场值，即可得到一个除前后两个端面外的矩形包络面。用矩形包络面上各测量点处的电场减去背景电场即可得到艇模在矩形包络面上的电场分布。

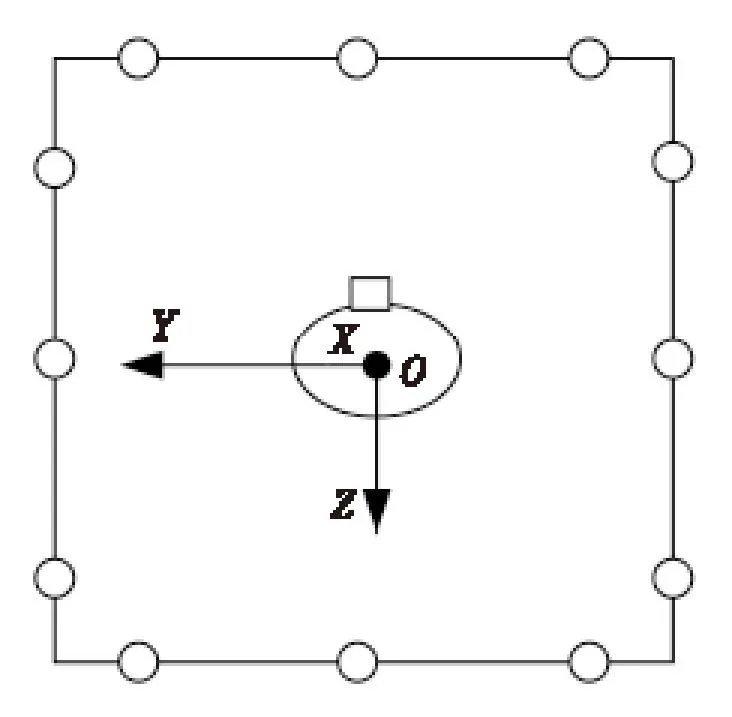
图6　潜艇与传感器位置示意图Fig.6　Schematic of position of submarine and sensor

3)根据所建立的静态电场边界元模型推算距潜艇左舷3m,水深0.2m,即直线 z=0.2m,y=3m,x∈(-8,8)m处的电场。

图7　电场强度测量值与边界元推算值的比较Fig.7　The comparision of electric field intensity betweenthe measured and the computed

3.2实测数据结果分析

根据等效偶极子理论[5-6]，实验中船模可以看做电场源点，z=0.2m,y=3m,x∈(-8,8)m直线处各点作为场点。以船模中心为对称轴，在偏离源点较近处电场模值出现大幅度衰减，偏离源点较远处衰减变弱。在该实验建立的笛卡儿坐标系中，船模中心坐标(0，0，0)，场点坐标(0，3，0.2)及(6，3，0.2)代入文献[5]中静电场分布解析公式验证，可以发现在船长约4倍处，静态电场强度模量衰减约75%，4倍以内衰减较快，4倍以外衰减变缓。该实验实测数据与文献[5]中直流电偶极子等效理论公式在相同源点与场点处计算结果一致，证明该实验是有效的。

3.3边界元模型换算数据分析

根据式(9)可知，电场强度与场点和源点之间的距离成反比。当场点与源点距离较近时，电场强度衰减越快；场点与源点距离较远时，电场强度衰减越慢。定性上来看，静态电场边界元模型推算的电场强度模值是符合静电场在海水中的衰减规律的。根据边界元模型换算数据显示，在船长约4倍处，静态电场强度模量衰减约75%，与实验实测数据衰减率接近，可以把船长4倍处看做电场强度模值衰减特征点。

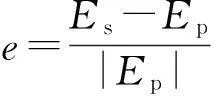
4结论

本文提出了基于边界元的舰船水下静态电场推算方法。该方法不局限于无限大平面，可对半无限域任意形状的闭合曲面建立边界面积分模型，并进一步采用长方体四个面近似闭合曲面建立水下静态电场边界元模型，基于该边界元模型进行水下静态电场的推算。实验验证和结果分析证明了基于边界元的水下静态电场推算方法的正确性和可靠性，其外推电场值与实测电场值相对误差为5%左右，能达到较高的换算精度，相比于无限大平面法的深度换算，更适宜指导工程实践。

基于边界元的舰船水下静态电场推算方法可以在以下方面做进一步改进：1)基于实际测量的原因，本文忽略了包络面的前、后两个端面，来近似封闭面，由于前后两端面面积较小，仿真结果表明误差不大，但仍会产生一定的计算误差。2)在对边界面进行剖分时，将每个面元中心点上的值作为该面元上的平均值，这会产生离散误差，因此小面元剖分得越细，面元越多，面元的面积越小，边界元推算的精度越高。3)当场点趋于源点时，边界面积分涉及到对奇异点的数值处理，边界面积分精度很大程度上依赖于奇异积分的计算精度，可以在对奇异积分处理方面对文中的边界元模型进行改进。

参考文献:

[1]ZAMANING.Boundaryelementsimulationofthecathodicprotectionsysteminaprototypeship[J].AppliedMathematicsandComputation, 1988, 26:119-123.

[2]IWATAM,HUANGY,FUJIMOTOY.ApplicationofBEMtodesignoftheimpressedcurrentcathodicprotectionsystemforshiphull[J].JoftheSocietyofNavalArchitectsofJapan, 1992, 171: 377-380.

[3]DOIGP,FLFWITTPEJ.Afinitedifferencenumericalanalysisofgalvaniccorrosion[J].Electrochem,1979,126(12):2057-2063.

[4]KASPERRG,APRILMG.Electrogalvanicfiniteelementanalysisofpartiallyprotectedmarinestructures[J].Corrosion, 1983, 39(5): 181-183.

[5]刘胜道.舰船水下电场的测试技术与电偶极子模型研究[D].武汉：海军工程大学, 2002：43-45.

[6] 刘文宝，王向军，嵇斗.基于电偶极子模型的舰船静电场深度换算[J].空军雷达学院学报，2010(6)：435-438.

[7] 刘忠乐，龚沈光.海水中稳恒电流电场的点电极计算模型[J].海军工程大学学报，2004，16(1)：35-39.

[8] 姜润翔，胡英娣，龚沈光.基于点电源的船舶静态电场深度换算方法研究[J].电波科学学报，2014，29(4)：685-693.

[9] 陈聪，李定国，龚沈光.基于拉氏方程的舰船静态电场深度换算[J].电子学报，2010，38(9)：2025-2030.

[10]李定国，陈聪，刘华波.舰船水下静态电场深度换算的格林函数法[J].海军工程大学学报，2012，24(3)：1-5.

[11] 陈聪，龚沈光，李定国.舰船静态电场深度换算方法[J].哈尔滨工程大学学报，2009，30(6)：719-722.

[12]胡英娣，龚沈光，闫永贵.一种新的船舶静态电场深度换算方法[J].海军工程大学学报，2013，10(25)：17-20.

[13]姚端正，梁家宝.数学物理方法[M].武汉：武汉大学出版社，2010:250-252.

摘要:针对基于无限大平面理论的深度换算在转化为数值积分后，对换算深度、测量点距及测量平面尺寸都有要求，若换算深度小于测量点距或测量平面尺寸接近换算深度时都会产生较大误差等问题，提出了基于边界元的舰船水下静态电场推算方法。该方法不局限于无限大平面，可对半无限域任意形状的闭合曲面建立边界面积分模型，进一步采用长方体四个面近似闭合曲面建立水下静态电场边界元模型，并利用该边界元模型进行了水下静态电场的推算。实验验证和结果分析证明了此方法的有效性，能达到较高的换算精度。

关键词:边界元；静态电场；半无限区域

Extrapolation of Vessel Static Electric Field Based on Boundary ElementHE Fang，WANG Xiangjun，GAO Junji

(Electrical Engineering College，Naval University of Engineering，Wuhan 430033，China)

Abstract:When the depth is less than?measuring distance, or the size of measuring plane is close to the depth, extrapolation based on the infinite plane will have a greater error. If extrapolation is based on the finite plane, a decrease in accuracy is caused. To solve this problem, a method of depth extrapolation of static electric field was proposed based on boundary element method in the semi infinite domain. The method was not limited to the infinite plane, but also could establish the boundary integral model for arbitrary closed surface in semi infinite domain. Static electric field boundary element model under water was built up based on four surface of rectangular approximated the closed surface, and the underwater static electric field could be calculated using this boundary element model. The submarine model experiment testified that this method was of higher precision and stronger operability.

Key words:boundary element; static electric field; semi infinite domain

中图分类号:TM46

文献标志码:A

文章编号：1008-1194(2015)06-0055-06

作者简介:何芳(1981—), 女,湖北荆门人，讲师, 博士研究生，研究方向：电场防护与隐身技术。E-mail:wskay1103@163.com。

基金项目:国家自然科学基金项目资助(41476153)

*收稿日期:2015-03-27