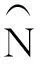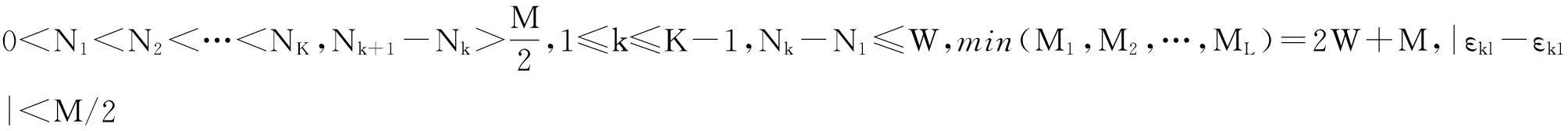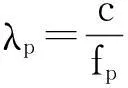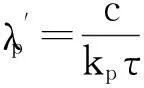空间欠采样下多个LFM信号方位估计新方法

叶陈诚, 梁红

(西北工业大学 航海学院, 陕西 西安　710072)

空间欠采样下多个LFM信号方位估计新方法

叶陈诚, 梁红

(西北工业大学 航海学院, 陕西 西安710072)

摘要：针对空间欠采样下多个LFM信号方位估计问题，提出了一种基于同时估计多实数的广义稳健中国剩余定理的方位解模糊方法。研究了忽略信号交叉项影响所需的条件及利用广义稳健中国剩余定理对多个LFM信号方位解模糊的原理和方法。仿真实例表明新提出在空间欠采样情况下对多个LFM信号目标同时解方位模糊的方法是有效的，方位估计的精度高，稳健性好。

关键词：空间欠采样；解模糊；广义稳健中国剩余定理；信号交叉项；多个LFM信号的方位角估计；蒙特卡罗方法

线性调频(linear frequency modulation，LFM)信号作为一种雷达，声呐等系统中常用的信号形式，对它进行检测和方位估计具有重要的意义。然而，奈奎斯特采样定理指出，在采用阵列对信号进行方位估计时，要求相邻阵元间距小于信号波长一半，高中心频率使LFM信号很难满足这个条件，而空间欠采样将会带来阵元间相位差的模糊值并因此难以估计出信号的方位。本文主要讨论解决多个LFM信号方位估计问题的方法。

大量文献对LFM信号方位估计问题进行了研究。其中，文献[1]提出了基于分数阶Fourier变换的单个LFM信号DOA估计方法，但没有考虑到多个LFM信号方位估计问题；文献[2]研究了基于欠采样下的单个超宽带LFM信号调制斜率和初始频率的估计方法，但是没有涉及到欠采样下多个LFM信号方位估计问题。文献[3-4]从数学角度深入研究了欠采样问题。文献[3]提出了重构单个实数的广义稳健中国剩余定理，并利用该定理解决了单源窄带信号的方位估计问题。文献[4]提出了同时估计多个实数的广义稳健中国剩余定理，并利用它解决了时间欠采样下多源窄带信号频率估计的问题。

受到文献[3-4]的启发，本文提出了一种空间欠采样下多个LFM信号方位估计的新方法，该方法以同时估计多个实数的广义稳健中国剩余定理(generalized robust Chinese remainder theorem, GRCRT)为基础，当被估计的多个LFM信号参数满足一定条件时，可以在较低信噪比下稳健的估计出信号的方位角。

1空间欠采样下多个LFM信号方位估计的问题分析

图1所示的是由L个阵元组成的均匀线列阵，P个来自远场的宽带信号的方位角的集合为θ={θ1,θ2,…,θP},1≤p≤P,θ1<θ2<…<θP。d为相邻阵元间距，则第l个阵元接收到的信号表示为

(1)

sp(t)=Apexp[j(2πfpt+πkpt2)],1≤p≤P

(2)

式中,Ap为信号幅度,为了讨论方便假设信号的幅度相同且幅值均为A,fp,kp分别为第p个信号的初始频率和调制斜率(已知),τl(θp)(1≤l≤L,1≤p≤P)为第l个阵元接收到第p个信号的延迟时间,τ1=0,w(t)是与信号无关的均值为0,方差为1的复高斯白噪声。

用采样频率fs对信号xl(t)进行采样,可以得到

(3)

图1　均匀线列阵模型

1.1LFM信号方位的估计

受到文献[2]中多个线性调频信号调制斜率估计方法的启发,本文希望把所有阵元上的信号转化为单频信号后再进行方位估计。方法如下:把每个阵元上采样后的信号xl(n)延时τ后,取τ=0.4T[2],与xl(n)共轭相乘,可以得到:

(4)

式中,N=τ*fs。从上面公式可以看出,右边第1项是多个频率为kpτ的正弦信号的叠加,需要估计它的信号的相位谱中包含的延迟信息nl进而估计出信号的方位;第2项是各个信号的交叉项;第3项和第4项是信号与噪声的交叉项;第5项是噪声的自相关项。假设信号与噪声是不相关的,而且高斯白噪声本身是相互独立的,因此经过把延迟后的信号与原信号共轭相乘基本达到了把非平稳的线性调频信号转化为平稳的单频信号的目的,但目前(4)式中右边第1项相位的估计还会受到信号交叉项的影响。1.2节将分析忽略交叉项影响的条件。

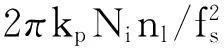
1.2信号交叉项对方位估计的影响分析

通过前面的分析可以看出,估计多个LFM信号的方位受到信号交叉项的影响,如果信号交叉项可以忽略,则可以得到每个阵元上的相位之后求得阵元间的相位差,进而估计出多个LFM信号的方位。现在讨论如何忽略交叉项的影响。

对于(4)式,包含每个阵元上信号相位信息的复正弦矩形脉冲信号的幅度谱的最大值可以表示为:

(5)

交叉项中任何一个线性调频信号的幅度谱的最大值可以表示为:

(6)

2同时估计多个实数的广义稳健中国剩余定理描述

设有k个正实数集合Φ={N1,N2,…,NK},N1

(7)

式中,M=gcd(M1,M2,…,ML)是L个模数M1,M2,…,ML的最大公约数, Γi和Γj互质,Γ1<Γ2<…<ΓL,1≤i≠j≤L。在实际应用中也可以选择互质的一组数的整数倍作为模数。

对于1≤l≤L,定义实数集合Φ模Ml的余数集合为:

(8)

但在许多应用场合,例如数字信号处理和雷达系统中,获得的rkl是有误差的,即

(9)

(10)

对得到的有误差的余数从小到大进行排序,即使

(11)

式中,α1<α1<…<αK。

定义qkl⎣rkl/M」,则可以得到。

定义Nk0⎣Nk/M」,则可以得到Nk0=nklΓl+qkl,即可以得到一个方程组:

(12)

根据上述定义,同时估计多个实数的广义稳健中国剩余定理可以表述为:

定理2假设定理1的条件成立,模数满足(7)式条件,Γi和Γj互质,1≤i≠j≤L。如果0≤max(N1,N2,…,NK)=NK

(13)

则求解(12)式中的方程组可以得到唯一一组解nkl。

(14)

估计的误差上限是:

(15)

参考文献定理1和定理2的证明[3]。

3空间欠采样下基于同时估计多个实数GRCRT的多个LFM信号方位估计

(16)

(17)

(18)式中,d0为一个固定值。

通过以上分析,P个线性调频信号方位角估计的步骤如下:

(1)从均匀线列阵中选择S组阵元,每组包含2个阵元,每组阵元的选择需满足GRCRT定理的要求;

(2)对其中1组阵元上的信号进行1次采样,采样后信号延迟与原信号共轭相乘把信号近似转化为多个频率为kpτ的单频信号的叠加,采用FFT算法和谱峰搜索,得到每个阵元上信号的频谱,相同频率的谱峰对应的相位之差即为对应的P个信号的1组相位差估计值;

(3)对其他组阵元上信号重复第2步直至获得P个信号的S个相位差,并且建立转化后的多个单频信号频率和相位差模糊估计值的对应关系;

(4)利用GRCRT定理分别估计出P个信号的无模糊方位角。

4仿真实验及结果

根据上述信号参数及GRCRT,在空间欠采样下分析两组阵元上的信号,第1组是1号阵元和6号阵元,第2组是1号阵元和5号阵元,即d16=5d,d15=4d。 设定常数d0=80d,则有d0/d16=16,d0/d16=20(对应GRCRT定理中M为4,Γ1和Γ2为4和5)。

图2　空间欠采样下信号方位估计曲线

为了验证在空间欠采样下所提方法进行多个宽带LFM信号方位估计的性能,仿真实验给出了信噪比变化时方位角的估计性能曲线。图2a)为估计的信号方位角与信噪比的关系曲线;图2b)为方位角估计的均方根误差与信噪比之间的关系曲线。图2a)和图2b)均是10 000次Monte-Carlo实验的结果。图中结果表明,在信噪比大于-5 dB并且参数的选择满足定理要求时,能利用同时估计多个实数的GRCRT定理稳健地重构多个宽带LFM信号的方位角。

5结论

本文提出了一种空间欠采样下多个LFM信号方位无模糊估计的方法。当被估计的LFM信号参数满足一定条件时，可以忽略信号交叉项对信号方位估计的影响，这时利用同时估计多个实数的GRCRT可以估计出无模糊的方位。仿真实验验证了所提出方法的有效性和稳健性，新提出的方法适用于空间欠采样下多个LFM信号的方位估计。

[1]张艳红，齐林，穆晓敏，陶然. 基于分数阶傅里叶变换的WLFM信号DOA估计[J]. 信号处理,2005,21(4A):57-60

Zhang Yanhong, Qi Lin, Mu Xiaomin, Tao Ran. DOA Estimation of WLFM Signal Based on Fractional Fourier Transform[J]. Signal Processing, 2005, 21(4A): 57-60 (in Chinese)

[2]沈显祥，叶瑞青，唐斌. 基于欠采样的宽带LFM信号参数估计[J]. 电波科学学报，2007，22(1)：43-46

Shen Xianxiang, Ye Ruiqing, Tang Bin. An Algorithm for Estimation of Wideband LFM Signal Parameters Based on Sub-Sampling[J]. Chinese Journal of Radio Science, 2007, 22(1):43-46 (in Chinese)

[3]Li Xiaowei, Liang Hong, Xia Xianggen. A Robust Chinese Remainder Theorem with Its Applications in Frequency Estimation from Undersampled Waveforms[J]. IEEE Trans on Signal Processing, 2009, 57(11): 4314-4322

[4]Liang Hong, Zhang Heng, Jia Ning. A Generalized Robust Chinese Remainder Theorem for Multiple Numbers and Its Application in Multiple Frequency Estimation with Low Sampling Rates[C]//Proc Int Conf Signal Processing, Communication and Computing,2011

An Effective Method for Estimation of DOAs of Mutiple LFM

Signals with Sub-Nyquist Spatial Sampling

Ye Chencheng, Liang Hong

(College of Marine Science and Technology, Northwestern Polytechnical University, Xi′an 710072,China)

Abstract:Aim. We propose a new approach to estimating DOAs(direction of arrivals) of multiple LFM signals with sub-Nyquist spatial sampling. Sections 1 through 3 explain our method of estimation mentioned in the title, which we believe is effective. In section 1，we analyze the process of estimating DOAs of multiple LFM signals with sub-Nyquist spatial sampling and obtain the condition for ignoring the effect of cross term. In section 2, we brief GRCRT(Generalized Robust Chinese Remainder Theorem) for multiple numbers proposed by us in Ref.4. In section 3, we obtain ambiguous phase differences of multiple LFM signals from several pairs of array antennas with sub-Nyquist spatial sampling; then we apply GRCRT to estimating the real DOA of each LFM signal. Section 4 presents a numerical example; the simulation results, given in Figs. 2, and their analysis show preliminarily that our new approach based on GRCRT for multiple numbers can indeed accurately and robustly estimate DOAs of multiple LFM signals.

Key words:autocorrelation, direction of arrival, efficiency, errors, estimation, fast Fourier transforms, frequency modulation, mean square error, Monte Carlo methods, sampling, signal to noise ratio, sensor arrays, time delay, wavelength; cross term, GRCRT(generalized robust Chinese remainder Theorem), LFM(linear frequency modulation), sub-Nyquist spatial sampling

中图分类号：TN911.7

文献标志码：A

文章编号:1000-2758(2015)05-0849-05

作者简介：叶陈诚(1992—)，西北工业大学硕士研究生，主要从事信号处理研究。

基金项目：国家自然科学基金(61379007)资助

收稿日期：2015-03-24