一种弹性机翼的颤振主动抑制与阵风减缓方法

刘祥, 孙秦

(西北工业大学 航空学院, 陕西 西安　710072)

一种弹性机翼的颤振主动抑制与阵风减缓方法

刘祥, 孙秦

(西北工业大学 航空学院, 陕西 西安710072)

摘要：由于航空器的弹性性质,飞行过程中飞行参数的不断变化会引发运动稳定性和阵风响应特性的改变。在设计颤振主动抑制或阵风减缓控制器的过程中,以某一飞行状态为基础设计出的控制律往往不能保证在一定飞行参数范围内的性能。针对此问题,首先通过非定常气动力有理拟合方法建立时域连续阵风响应状态空间方程,再考虑模型随马赫数和动压的变化特性建立线性参数变化(LPV)模型。最后以线性参数变化模型为基础构造了包含动压和马赫数参数不确定性的线性分式变换模型,并设计了机翼颤振主动抑制与阵风减缓鲁棒控制器。结果表明,对于算例机翼,其在马赫数0.5～0.7范围内的颤振动压平均增大10%,且在飞行参数不断变化的时域仿真中,翼尖过载的均方根值降低51.4%。

关键词：非定常气动力;线性参数变化模型;鲁棒控制;颤振主动抑制;阵风减缓

作为随控布局飞机设计中的一项关键技术,颤振主动抑制方法一直受到众多研究者的强烈关注。随着控制理论的发展,颤振主动抑制的控制律设计方法也逐渐从最优控制过渡到鲁棒控制。鲁棒控制通过描绘对象的不确定性,并在不确定性允许的摄动范围内综合设计控制律以使系统保持稳定性和性能鲁棒,其中的结构奇异值方法则是在H∞理论上发展起来的一种重要技术,且已经成为颤振主动抑制的一个有效工具[1-3]。因飞行器的颤振边界依赖于动压和马赫数等飞行参数,一种应用于颤振主动控制律设计的简单方法便是在μ框架中引入对飞行参数的扰动并确定使系统不稳定的最小参数变化。为进行气动伺服弹性系统的稳定性分析,Lind等[4]建立了包含动压不确定性的线性分式变换模型。Moulin[5]在气动伺服弹性系统的状态空间模型基础上,引入空速和空气密度扰动并建立线性分式变换模型,以此为基础设计了颤振抑制的μ控制器。为便于设计鲁棒控制器,Qian等[6]在Moulin的方法的基础上通过模型变换有效降低了不确定块的维数,并设计了颤振抑制效果更好的鲁棒控制器。但前述的模型均以刚性机翼或低速机翼为研究对象,很少以亚声速范围内的机翼为研究对象。其中一个重要原因是在亚声速范围内马赫数对广义非定常气动力系数的影响无法解析表达,难于构造相应的线性分式变换模型。除鲁棒控制方法外,变增益控制[7]、非线性控制[8]、自适应控制[9]等方法也在逐渐获得深入研究并应用于颤振主动抑制。

Blue等[10]对一个二元翼段建立了随马赫数和动压变化的近似线性参数变化模型,在较大的飞行范围内都取得了足够的精度,但没有考虑广义气动力系数的变化特征和弹性模态的影响。本文克服了上述缺点并以线性参数变化模型为基础构造了包含动压和马赫数参数不确定性的线性分式变换模型,随后结合鲁棒控制理论设计了用于颤振抑制和阵风减缓的μ控制器,并对结果进行了时域仿真验证。

1气动伺服弹性系统模型

开环气动伺服弹性系统模型是控制器设计的出发点。在构造系统的开环运动方程之前,需要先将频域的广义气动力系数从频域有理延拓为拉氏变量s的有理函数,这可以通过最小状态法[11]来实现,其拟合公式为

基于控制面和阵风激励的弹性体状态空间方程为

可简写为

(3)

式中

(4)

式中，ξ为机翼弹性模态对应的n维广义坐标,xa为na维气动力状态扩充项,Mξξ广义质量矩阵,Kξξ为广义刚度矩阵,Cξξ为广义阻尼矩阵,Mξδ为结构模态和控制面的耦合质量阵,δ为控制面偏转模态坐标,wg为垂直阵风速度。

以翼尖加速度为输出时,输出方程为

(5)

式中Φ为翼尖节点的模态向量。

舵机的传递函数可表示为

(6)

式中，Aac、Bac和Cac分别表示系统矩阵、输入矩阵和输出矩阵,xac为舵机状态向量,uc为舵机输入信号。

连续阵风的状态空间方程形式为

(7)

式中各矩阵可由Dryden阵风模型[12]或VonKarman阵风模型[12]得到。其中Ag、Bg、Cg和Dg分别表示系统矩阵、输入矩阵、输出矩阵和直接转换矩阵,xg为阵风状态向量,η为白噪声输入信号。

引入舵机和阵风环节,可得到弹性机翼的开环状态空间方程

(8)

可简写为

(9)

式中

(10)

2随马赫数和动压变化的线性参数变化模型

由(2)式、(3)式和(8)式可知,矩阵A和B中部分元素受马赫数Ma、空速V和空气密度ρ的影响,其中马赫数通过广义气动力系数矩阵间接影响系数矩阵的取值。但在标准大气情况下,Ma、V和ρ三者的取值可通过2个独立变量Ma和q得到,因此(9)式可描述为

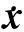
(11)

式中

(12)

式中，Δq和ΔMa分别表示马赫数和动压的最大变化量,δ1和δ2分别表示动压和马赫数的归一化不确定性,取值范围为[-1,1]。

(11)式中飞行参数对系数矩阵的影响可通过(13)式来近似[10]以构造线性参数变化模型

(13)

在给定Ma和q的取值范围后,(13)式右端的各未知系数矩阵可通过最小二乘法求解得到。

(14)

3线性分式变换模型

为便于鲁棒控制器的设计,需要将上节得到的线性参数变化模型转换为线性分式变换模型。首先将(14)式重组如下

(15)

再定义如下的输入和输出变量z和v

显然有

v=Δ·z

(17)

(18)

现将(16)式代入(15)式可得

(i=1,2,…n+na)

(19)

再将(19)式代入(9)式并结合(16)式可得

(20)

(20)式中各矩阵可简单推得,此处恕不详述。

y=Cyx+Dyuu+Dyvv

(21)

此处省略(21)式右端各矩阵的详细描述。

组合(20)式与(21)式可得

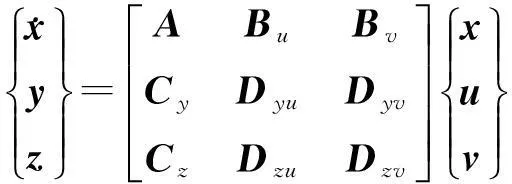
(22)

令P(s)为S的拉氏变换,则有

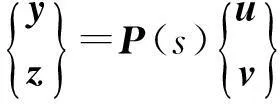
(23)

组合(23)式和(17)式可得

y=Fl(P,Δ)u

(24)

式中，Fl(P,Δ)表示P(s)与Δ构成的下线性分式变换,其表达式见下式,可用图1表示。

Fl(P,Δ)=P11+P12Δ(I-P22Δ)-1M12

(25)

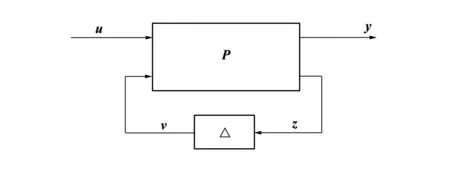
图1　线性分式变换模型

为便于控制器设计,需要将不确定块Δ归一化以使其所有元素绝对值不大于1,这可在(12)式的基础上通过线性分式变换将Fl(P,Δ)转换为Fl(P1,Δ1),其中为Δ1为归一化的不确定块。

至此已构造出能够计及飞行参数变化的统一模型,下面将通过算例构造模型并设计用于颤振主动抑制和阵风减缓的鲁棒控制器。

4算例

4.1开环颤振分析

算例机翼的有限元模型如图2所示,机翼根部固支。采用MSC/Nastran软件计算得到前9阶结构模态,其中前4阶模态特征如表1所示。采用ZAERO软件计算各马赫数下的非定常气动力系数,图3给出了机翼气动力模型及控制面的位置。机翼在马赫数0.5～0.7范围内由P-K法计算得到的颤振边界如表2所示。

表1　机翼模态特征

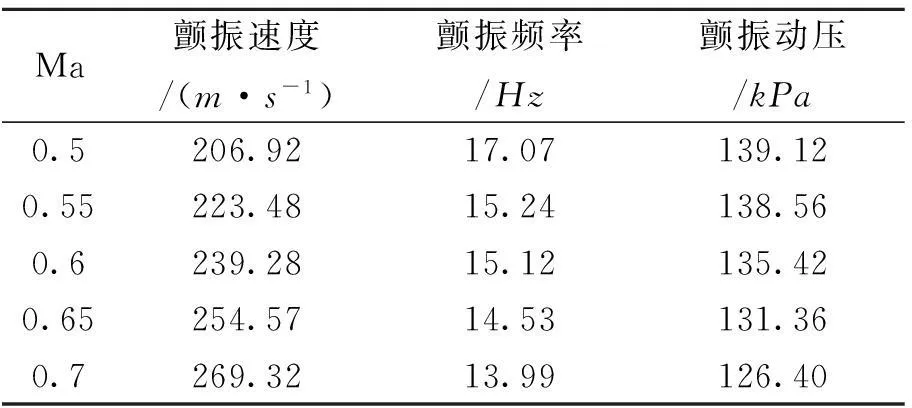
表2　机翼颤振边界

在构造随动压和马赫数变化的线性参数变化模型时,需要在给定的飞行范围内选取部分飞行状态并用最小二乘法求解(13)式右端的各系数矩阵。本文选取的飞行状态点如表3所示。从表3可以看出,开环颤振点附近的动压增量被适当缩小以改善精度。在构造各飞行状态点的状态空间模型时,对非定常气动力系数的有理拟合均采用4个滞后根,采用Dryden连续阵风模型,阵风强度为1.5m/s,阵风尺度为760m,输出为翼尖前缘点的过载,并将其作为反馈控制器的输入信号。舵机传递函数见(26)式

(26)

为验证拟合结果的精度,本文比较了线性参数变化模型和原状态空间模型在各马赫数下的颤振点特征。结果表明颤振动压误差均小于1%,这说明线性参数变化模型的精度是足够的。图4比较了部分飞行条件下,原状态空间模型与线性参数变化模型中翼尖前缘的阵风频响特性曲线。从图中可以看出两者几乎一致,这从另一个侧面验证了模型的精度。

表3 飞行状态点Ma动压/kPa0.51001251341441650.551001251331431650.61001251301401650.651001261361411650.7100120131140165

4.2μ控制器设计

对于当前模型,反馈控制的主要目标是抑制开环气动弹性系统的颤振及减缓阵风响应。在设计鲁棒控制律之前,需要构造完整的系统模型。图5给出了闭环鲁棒控制模型的结构,其中K即为待设计的鲁棒控制器。图中P1即为名义系统模型,Δ1为代表动压和马赫数不确定性的且维数为39×39的对角不确定块,Wy为翼尖过载的输出加权函数,表达式为

(27)

因连续阵风频谱主要集中于低频范围,因此在低频范围施加较高的权重能够充分发挥控制器阵风减缓的能力。本文将低频范围取为0～70rad/s,计算可得突风到翼尖过载的传递函数在稳定飞行范围内的峰值为0.04,则为了将对应飞行状态下的翼尖过载降低至少50%,需将Wy的系数取为2/0.04。

图5中wn代表传感器的量测白噪声信号,添加输出噪声有2个方面的作用:①提高鲁棒控制器的抗噪声能力;②完整化模型结构以避免控制器设计过程中的可能出现的数值问题[13]。ε为对量测噪声的加权小量,取值为0.001。

Wu为舵面控制信号的输出加权函数。为抑制翼尖的高频振荡部分和量测噪声中的高频信号引起的舵面偏转信号,需要对舵面控制信号的高频部分施加较高的权重,本文取为

(28)式中，Wu的系数为突风白噪声输入到舵面控制信号闭环传递函数最大允许增益的倒数。

图5中的模型可通过Matlab鲁棒控制工具箱[14]中的sysic命令转换成适于鲁棒控制器设计的结构。取Ma0=0.5,ΔMa=0.1,通过多次调整,在q0=115 kPa且Δq=15 kPa时控制器效果达到最佳。最终的鲁棒控制器通过平衡截断法[14]被降至11阶,且闭环系统的最大μ值为0.977,达到鲁棒稳定性和鲁棒性能要求。下节将通过闭环颤振及阵风响应分析进一步检验μ控制器的性能。

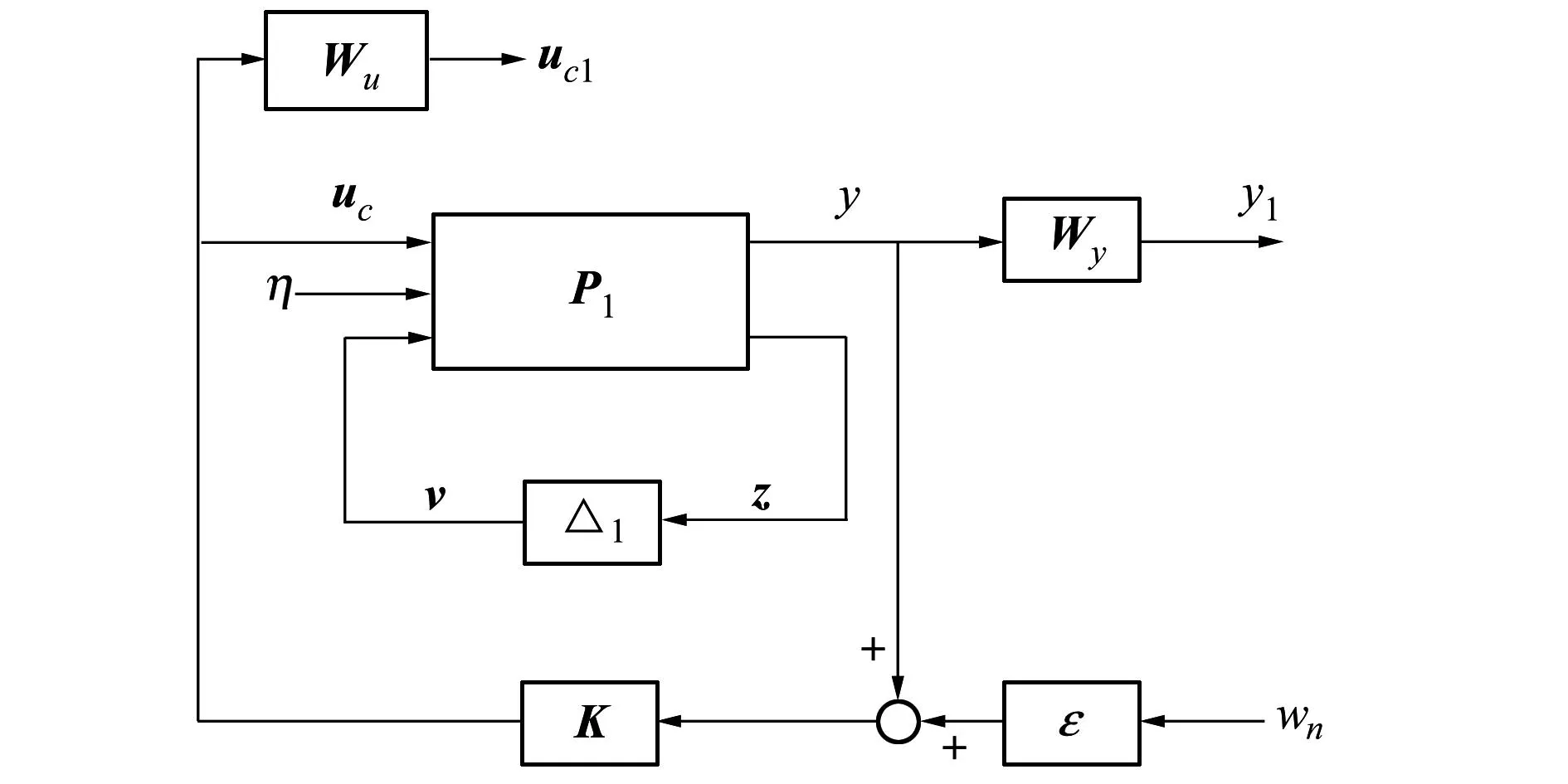
图5　闭环鲁棒控制模型结构

4.3闭环颤振及阵风响应分析

图6给出了机翼在马赫数在0.5～0.7范围内开环系统和闭环系统的颤振边界,从图中可以看出,鲁棒控制器将颤振动压在给定范围内平均提高了约10%。

为验证μ控制器的阵风减缓效果,令飞行马赫数在20s内从0.7线性变化到0.5,同时动压从100kPa线性变化到130kPa,易知在此过程中开环和闭环系统都是稳定的。图7给出了开环和闭环系统的翼尖过载时域响应。从图7中可以看出控制器有明显的阵风减缓效果,开环系统的翼尖过载均方根为1.07g,而闭环系统为0.52g,减小了51.4%。

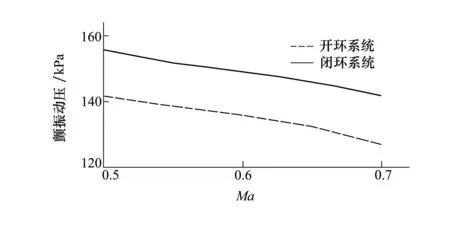
图6　开环及闭环颤振边界

图8给出了闭环系统的舵面转角和速度响应,从图中可以看出,控制面的转角和速度均在合理范围内,这也可以为舵机的选择提供参考。

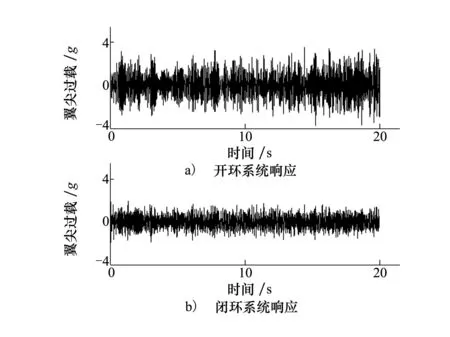
图7　飞行参数变化过程中的翼尖过载时域响应

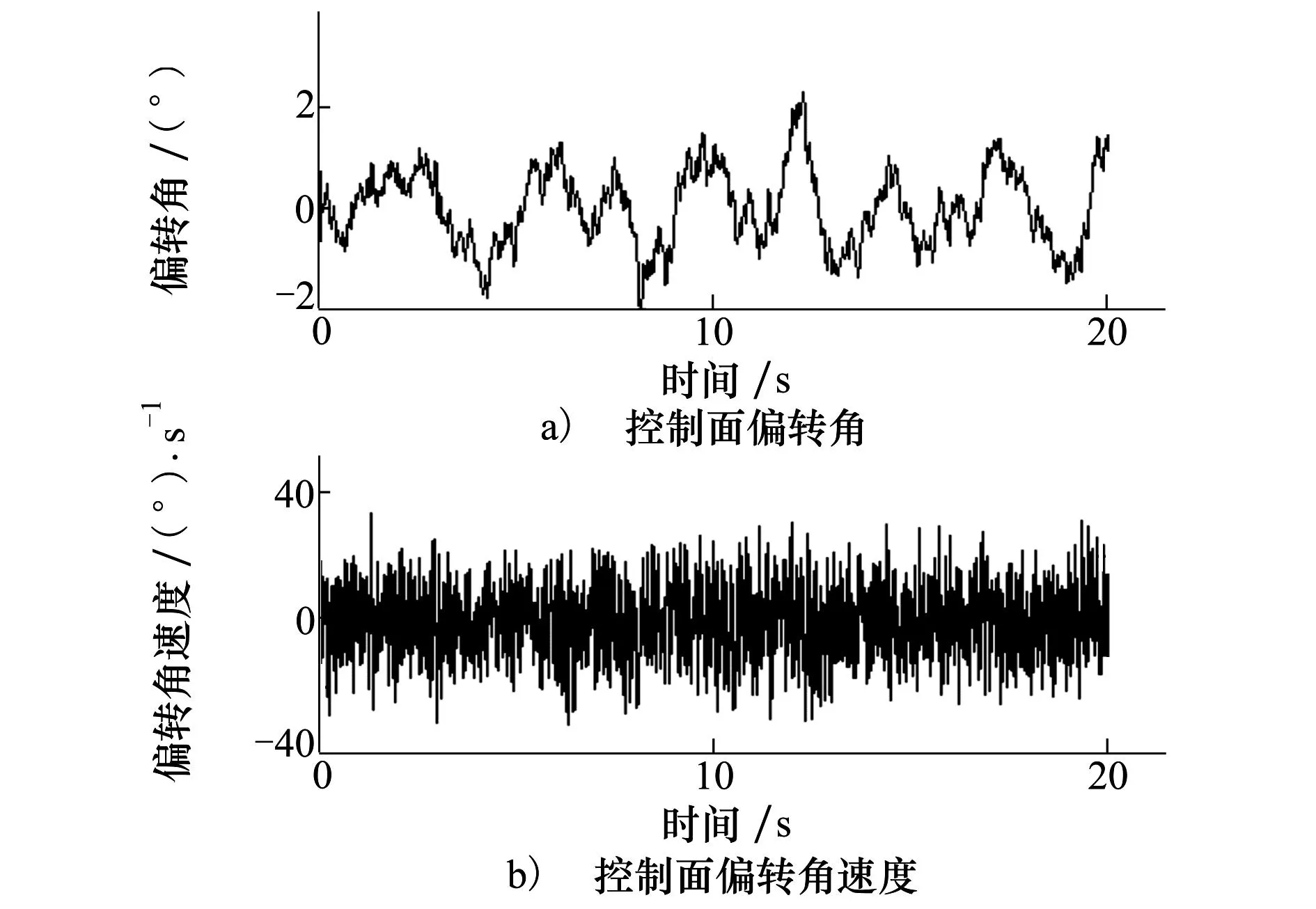
图8　飞行参数变化过程中的控制面响应

5结论

提出了一种亚声速下弹性机翼的颤振主动抑制与阵风减缓方法。因机翼的非定常气动力同时受马赫数和动压的影响,本文以线性参数变化模型为基础构造了含马赫数和动压不确定性的线性分式变换模型。最终设计出的鲁棒控制器,不仅将马赫数0.5～0.7范围内的颤振动压平均提高10%,还有效减缓了机翼的阵风响应。

参考文献：

[1]BorglundD.RobustAeroelasticStabilityAnalysisConsideringFrequency-DomainAerodynamicUncertainty[J].JournalofAircraft, 2003, 40(1): 189-193

[2]KarpelM,MoulinB,IdanM.RobustAeroservoelasticDesignwithStructuralVariationsandModelingUncertainties[J].JournalofAircraft, 2003, 40(5): 946-954

[3]BorglundD.Theμ-kMethodforRobustFlutterSolutions[J].JournalofAircraft, 2004, 41(5): 1209-1216

[4]LindR,BrennerM.AeroelasticandAeroservoelasticModels,RobustAeroservoelasticStabilityAnalysis:FlightTestApplications[M].London:Springer, 1999: 55-63

[5]MoulinB.RobustControllerDesignforActiveFlutterSuppression[R].AIAA-2004-5115

[6]QianWM,HuangR,HuHY,etal.NewMethodofModelingUncertaintyforRobustFlutterSuppression[J].JournalofAircraft, 2013, 50(3): 994-998

[7]BarkerJM,BlalasGJ,BluePA.Gain-ScheduledLinearFractionalControlforActiveFlutterSuppression[J].JournalofGuidance,Control,andDynamics, 1999, 22(4): 507-512

[8]RonchAD,TantaroudasND,JiffriS,etal.ANonlinearControllerforFlutterSuppression:fromSimulationtoWindTunnelTesting[R].AIAA-2014-0345

[9]CassaroM,BattipedeM,MarzoccaP,etal.ComparisonofAdaptiveControlArchitecturesforFlutterSuppression[J].JournalofGuidance,Control,andDynamics, 2015, 38(2): 346-355

[10]BlueP,BalasGJ.LinearParameter-VaryingControlforActiveFlutterSuppression[R],AIAA-1997-3640

[11]AzoulayD,KarpelM.CharacterizationofMethodforComputationofAeroservoelasticResponsetoGustExcitation[R].AIAA-2006-1938

[12]HoblitFM,GustLoadsonAircraft:ConceptsandApplications[M].WashingtonDC,AmericanInstituteofAeronauticsandAstronautics,Inc, 1988

[13]DoyleJC,GloverK,KhargonekarP,etal.State-SpaceSolutionstoStandardH2andH∞ControlProblems[C]//IEEETransonAutomaticControl, 1989: 831-847

[14]MooreB.PrincipalComponentAnalysisinLinearSystems:Controllability,Observability,andModelReduction[C]//IEEETransonAutomaticControl, 1981: 17-31

A Robust Active Flutter Suppression and Gust

Alleviation Method for Flexible Wing

Liu Xiang, Sun Qin

(College of Aeronautics, Northwestern Polytechnical University, Xi′an 710072, China)

Abstract:The stability characteristics and dynamic responses of a flexible wing vary with flight conditions. During the design process of a controller for active flutter suppression or gust alleviation, the controller’s performance cannot be sustained when flight conditions change if it is designed on the basis of a single flight condition. To solve this problem, the time domain state-space model is firstly built up with rational function approximation of the unsteady aerodynamics, then the model’s dependence on Mach number and dynamic pressure is taken into account by constructing a linear parameter-varying (LPV) model. A linear fractional transformation model is finally built up on the basis of the LPV model; after which a robust controller is designed for active flutter suppression and gust alleviation. The results on a test wing show that the flutter dynamic pressure increases about 10% when the Mach number varies between 0.5 and 0.7. As can be seen from the simulation results, when the flight parameters keep varying, the root-mean-square of the wing tip overloads decreases by 51.4%.

Key words:acceleration, closed loop control systems, computer software, controllers, damping, design, dynamic response, finite element method, flexible wings, flow velocity, flutter, Laplace transforms, least squares approximations, Mach number, matrix algebra, mean square error, pressure, robust control, stability, transfer functions, wind effects; active flutter suppression, gust alleviation, linear parameter-varying (LPV) model, unsteady aerodynamics

中图分类号：V215.3

文献标志码：A

文章编号:1000-2758(2015)05-0804-07

作者简介：刘祥(1991—)，西北工业大学博士研究生，主要从事飞行器气动伺服弹性系统研究。

基金项目：中航工业产学研创新项目(Cxy2010xG18)资助

收稿日期：2015-04-22