基于附加频移跳频的方案设计及其性能分析

全厚德，李思奇，崔佩璋，严仕浩

（1.军械工程学院，石家庄050003；2.解放军75130部队，广西贵港537000；3.解放军77552部队，西藏林芝860500）

基于附加频移跳频的方案设计及其性能分析

全厚德1，李思奇2，崔佩璋1，严仕浩3

（1.军械工程学院，石家庄050003；2.解放军75130部队，广西贵港537000；3.解放军77552部队，西藏林芝860500）

为了提高跳频系统的抗预测性能，增大抗跟踪干扰能力，提出了基于附加频移的跳频通信。在给定跳频带宽内，该方案通过双序列的控制输出射频频率来提高其跳变复杂度，从而增大敌方对于跳频序列的正确建模和预测难度。基于混沌特性的分析方法，对采用L-G非连续抽头模型和Logistic-Kent级联映射构造的合成跳频序列的复杂度进行了计算，与相同模型下构造的常规跳频序列相比，基于附加频移的跳频通信均具有更大的复杂度。

附加频移，跳频序列，混沌特性，复杂度

0 引言

跟踪干扰是跳频通信的最大威胁，一旦实施成功，将使跳频通信陷入瘫痪。跟踪干扰的实施主要与跳速、跳频图案、组网方式以及干扰机与通信双方的地域几何关系有关。而对于干扰方，能够有效实施跟踪干扰的前提是对跳频序列进行正确建模和预测。

为了提高跳频系统的抗破译性能，文献［1-4］提出了多种基于混沌映射和宽间隔跳频序列的构造方案。但是常规跳频序列均源自单一的确定性模型，文献［5-6］采用Massey算法和神经网络的预测模型能够对基于移位寄存器和混沌映射产生的跳频序列进行有效预测，其单步和多步预测的有效预测率在90%和70%以上，给常规跳频通信带来了巨大的威胁和挑战。

为了提高现有常规跳频系统的抗破译性能，本文提出了基于附加频移的跳频通信，通过双序列的控制来提高其频率跳变的复杂度，从而增大敌方对于跳频序列正确建模和预测难度。

1 基于附加频移的跳频通信模型

1.1 基本原理

设给定跳频带宽为W，将带宽均分成P个跳频区间，每个区间内设置q个频点，设最小信道间隔为Δfm，则有：

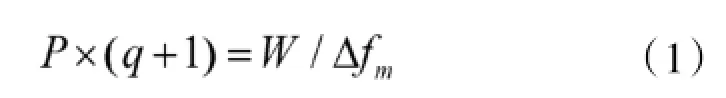
分别用两个跳频序列Su和Sv控制P个跳频区间起始频率的伪随机跳变和q个频点的伪随机跳变，这里称Su为主序列，Sv为附加序列。最后通过Su控制的频率fi（i=0，1，2…，P-1）和Sv控制的频率k×Δfm（k=0，1，2，…，q-1）的叠加，形成最后的射频频率fi+k×Δfm。如图1所示。

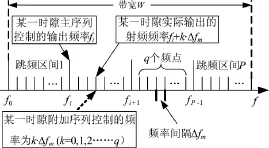
图1 射频频率生成示意图

设主序列Su控制的P个载频的频率集合A={fm（0），fm（i），…，fm（P-1）}，则附加序列Sv控制的q个载频的频率集合B={0，fn（0），fn（i），…，fn（q-1）}，周期长度为L的主序列Su和附加序列Sv可表示为Su= {su（0），…，su（i），…，su（L-1）}，其中su（i）={0，1，2，…，p-1}，Sv={sv（0），…，sv（i），…，sv（L-1）}，其中sv（i）= {0，1，2，…，q}。主序列Su和附加序列Sv控制的跳频码与载频集合A和B之间的映射函数可设为F（·）和H（·），F（·）可表示为：

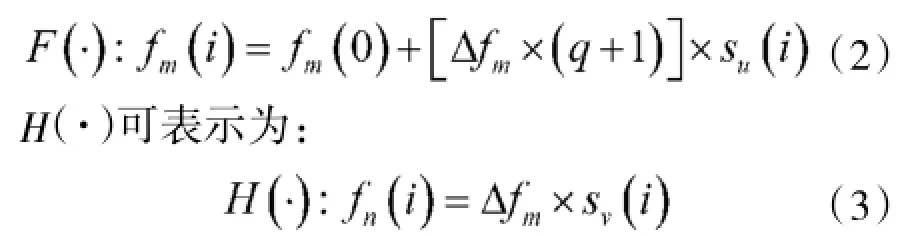
则实际输出的射频频率为fm（i）+fn（i）。

1.2 实现方案

由基于附加频移跳频的基本原理，可得出其收发双方的实现方案，如图2所示。基于附加频移的跳频通信与常规跳频通信系统不同的是射频频率的合成方案，可以看到其原理框图中增加了一个跳频序列发生器、一个频率合成器和一个带通滤波单元。

TOD和密钥共同决定了主序列Su和附加序列Sv的生成，主序列Su从区间频率表中取出频率控制码按照式（2）的映射函数控制频率合成器1在不同时隙输出伪随机跳变的区间起始频率fm（i），附加序列Sv从附加频移表中取出频率控制码按照式（3）的映射函数控制频率合成器2在不同时隙输出伪随机跳变的附加频率fn（i），两频率信号通过混频器1和带通滤波后可得到叠加的射频频率fm（i）+fn（i）。

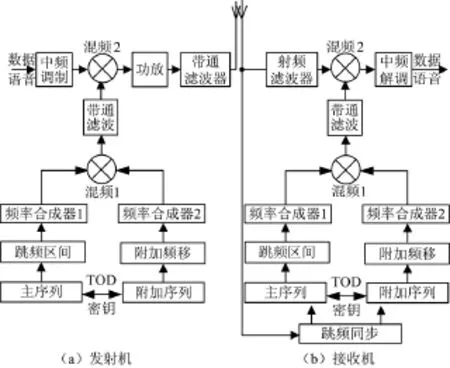
图2 基于附加频移的跳频通信原理框图

2 基于混沌特性的跳频序列复杂度计算

跳频序列均源于某种确定性模型，而混沌理论是对系统产生不规则行为的确定性认识，因此，可用混沌理论对跳频序列进行混沌动力学特性分析［7］。本文基于实际得到的跳频序列，分析其混沌特性，用关联维数度量其复杂度。如果跳频序列满足文献［8］指出的具有小数维的奇异吸引子和正的李雅普诺夫（Lyapunov）指数，则表明具有混沌特性。计算的流程如图3所示。

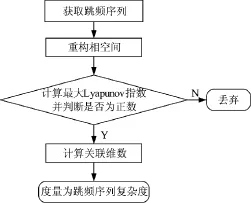
图3 跳频序列复杂度计算流程图

2.1 跳频序列的相空间重构

相空间重构是从时间序列出发创建的一个多维状态空间，它保持了不动点特征值、吸引子维数和轨迹的Lyapunov指数等几何不变量的不变［9］。

根据F.Takens的延迟嵌入定理［10］，设观测到的跳频序列为{x1，x2，…，xn}，对该跳频序列进行延迟采样，设延迟时间间隔为，则可将跳频序列延拓为一个m维的相空间：

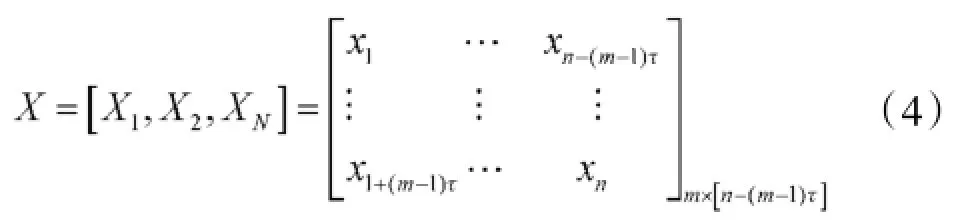
其中相空间中的每一列向量为：

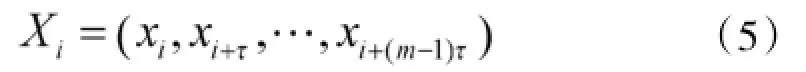
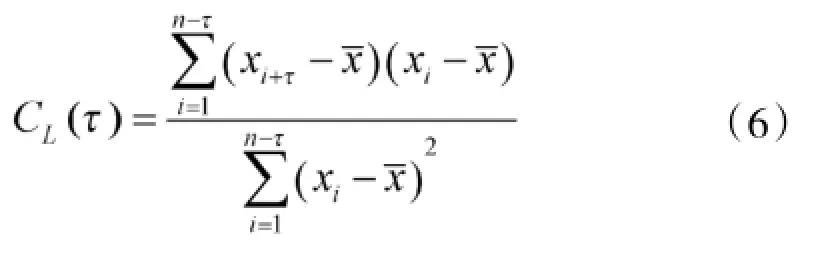
其中，x为跳频序列的平均值，通常取C（L）从起始到第一个斜率由负转正的为延迟时间间隔。

2.2 最大李雅普诺夫（Lyapunov）指数

最大Lyapunov指数是判断跳频序列是否为混沌系统的重要参数，如果最大Lyapunov指数是正的，意味着相邻轨线按指数发散，即系统是混沌的。

由观测时间序列计算最大Lyapunov指数的方法主要有A.Wolf等提出的轨线法［11］和Rosenstein等提出的小数据法［12］等。由于Wolf法需要较大的数据长度，计算结果受各种参数影响，实现较困难。本文采取文献［13］提出的基于Rosenstein改进的小数据量Kantz法计算最大Lyapunov指数。

记重构相空间中一对向量为：

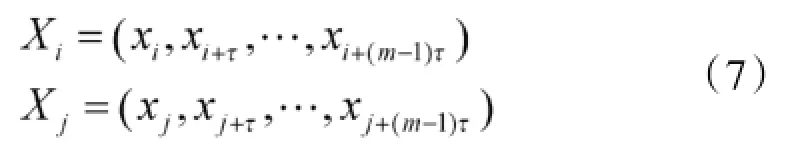
则它们之间的欧式距离为‖Xi-Xj‖，记Xi'为相空间n-（m-1）个列向量中与Xi最近的点，记di=‖Xi-Xi'‖。取一适当的时间步长或演化时间k，则di经过k个离散时间步长后的距离记为d（ik）。则最大Lyapunov指数可表示为：

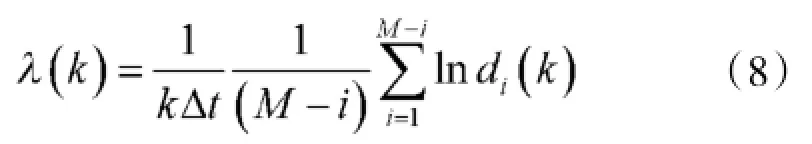
2.3 关联维数

关联维数刻画了相空间中点的分布，是系统复杂程度一种很好的度量。于是可通过计算重构相空间的关联维数来度量跳频序列的复杂度。

由观测得到的跳频序列，可由P.Grassberger和I.Procaccia给出的G-P算法直接计算［14-15］。设在m维的重构空间中，W表示除Xi本身外到Xi的距离小于r（r为一个小的正数）的Xj的点数。

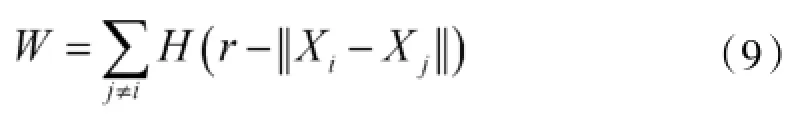
其中，H（·）为Heavside函数，满足：

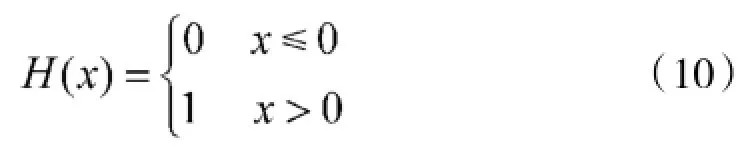
则定义重构的跳频序列的关联积分为：

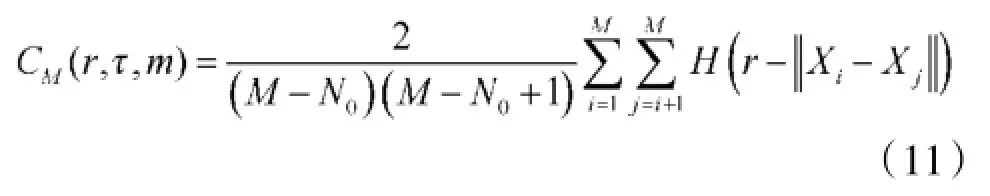
其中，N0=（m-1）+1，C（Mr，，m）描述了距离小于r的对点数的分布情况，如果在r的某一区间段内，有：

则称d是关联维数，它近似刻画了产生跳频序列的系统复杂程度的某种维数。对观测得到的跳频序列，可在r的某一区间段内通过对数lnCM（r，，m）-lnr图观测的方法求出关联维数d。

3 数值计算及仿真分析

为了计算附加频移跳频序列的复杂度，现给出其合成序列的计算公式，由式（2）和式（3）可得到实际输出的射频频率为fm（i）+fn（i），将射频频率转化为合成序列Su+v，其映射函数K（·）可表示为：

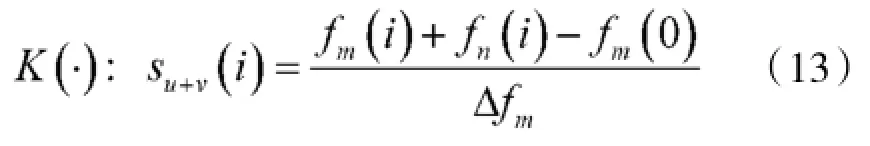
则长度为L的合成序列Su+v可表示为Su+v={su+v（0），…，su+v（i），…，su+v（L-1）}，其中su+v（i）={0，1，2，…，P×（q+1）-1}。

3.1 基于L-G模型构造的跳频序列

本文采用L-G非连续抽头模型构造跳频序列［16］，其原理如图4所示。

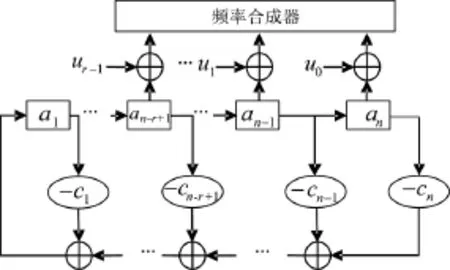
图4 L-G非连续抽头模型

取r个非相邻级控制跳频，即可产生2r个频隙的跳频序列，关系运算式为：

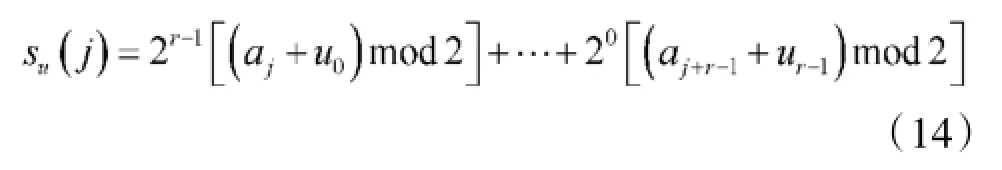
在超短波波段（30 MHz～87.975 MHz）内，将基于附加频移跳频的频率数设为256个，则主序列控制的跳频区间数P和区间内频率数q可有多种组合，首先取P=8，q=31，即构造8个跳频码的主序列Su和32个跳频码的附加序列Sv来构成256个跳频码的合成序列Su+v。

基于17阶的m序列（序列长度为217-1），由图4的L-G非连续抽头模型，分别取3个和5个非相邻级控制，即可构造8个跳频码的主序列Su和32个跳频码的附加序列Sv，设频段起始频率fm（0）为30 MHz，信道间隔Δfm为25 KHz，根据式（13）可得到256个跳频码的合成序列Su+v。基于同一m序列和L-G模型，取8个非相邻级控制，构造了相同序列长度的256个跳频码的常规跳频序列Sc。

分别从两跳频序列中选取5 000个跳频码进行归一化处理，形成［0-1］区间的时间序列。首先对两序列进行相空间重构，由式（6）可得出两序列的自相关函数CL（）与延迟时间的关系如图5和图6所示。

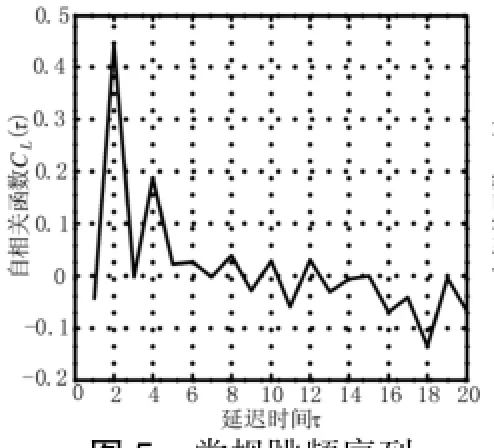
图5 常规跳频序列延迟时间计算

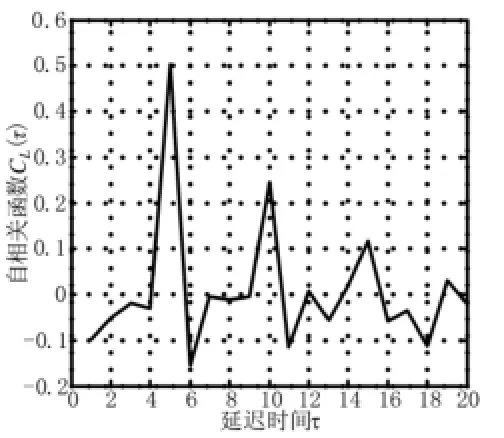
图6 合成跳频序列延迟时间计算

取C（L）从起始到第一个斜率由负转正的为延迟时间间隔，则由图5和图6可知，常规跳频序列进行相空间重构时的延迟时间=3，而基于附加频移的跳频合成序列的延迟时间=4。

对跳频序列进行相空间重构后，由式（8）可求取两序列的最大Lyapunov指数。取不同的演化时间k可求出不同的lndi（k）的平均值＜lndi（k）＞。本文取重构维数m=7，8，9，Δt=1，图7和图8给出了两跳频序列的＜lndi（k）＞-kΔt曲线。

对于混沌系统，其＜lnddi（k）＞-kΔt曲线有一段比较平直的区域，该段区域的斜率就是最大Lyapunov指数λ。当重构维数增加到一定程度后，不同重构维数对应的平直区域大致相同，图7和图8中的虚线表示＜lndi（k）＞-kΔt曲线的平直区域。求出两平直区域的斜率可近似表示两序列的最大Lyapunov指数，经计算，λ1=0.068，λ2=0.086。

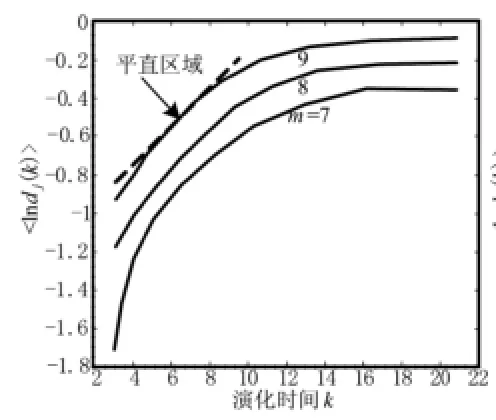
图7 常规跳频序列的最大Lyapunov指数计算

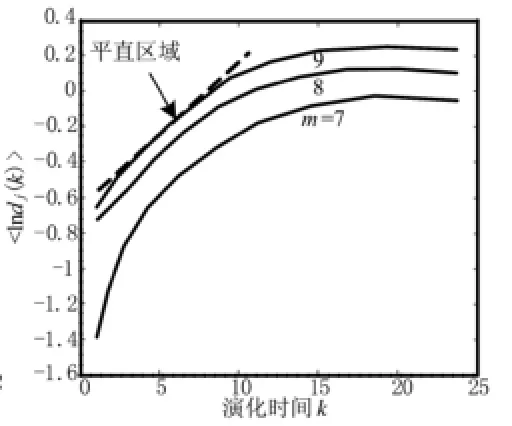
图8 合成跳频序列的最大Lyapunov指数计算

由式（11）可作出对数lnC（Mr，，m）-lnr图，如图9和图10所示，进而可计算其关联维数。

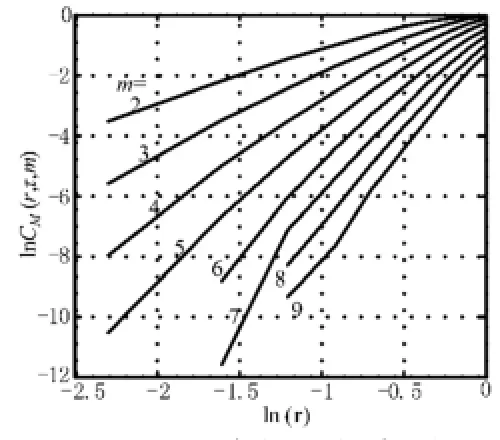
图9 常规跳频序列关联维数计算

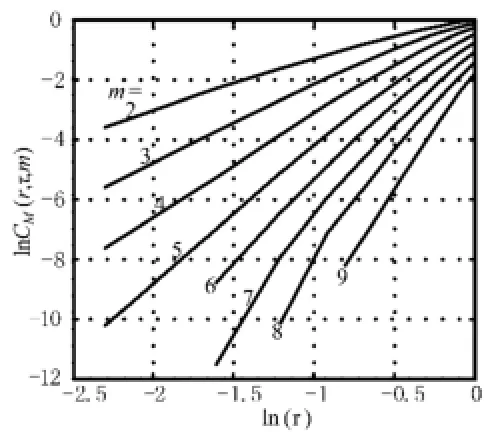
图10 合成跳频序列关联维数计算

由图9和图10可知，当重构维数增加到一定程度后，lnCM（r，，m）-lnr的斜率会趋于稳定值，该稳定值就是关联维数d。经计算，d1=6.777，d2=7.427。

基于同一L-G模型，还可选取其他区间数P和区间内频率数q的组合来构成其合成序列，以增大应用的灵活性和敌方破译的难度，其复杂度计算值如表1所示。

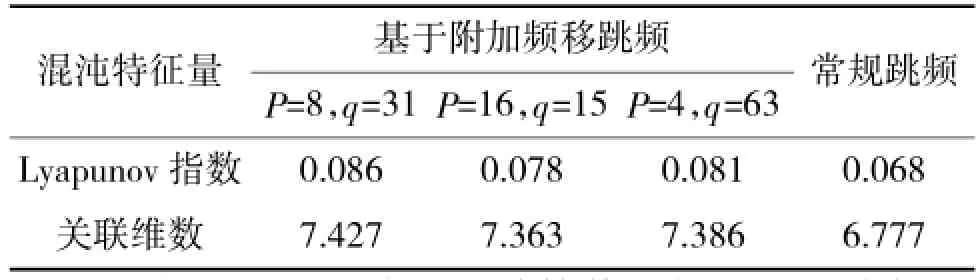
表1 混沌特征量计算值

由表1的混沌特征量计算值可知，基于附加频移跳频3种不同区间数和区间内频率数的组合构成的合成序列和常规跳频序列均具有正的最大Lyapunov指数，其关联维数都是有限的正数，则说明其跳频序列均具有混沌特性。由关联维数的计算值可知，基于附加频移跳频3种不同组合构成的合成序列的最小值为7.363，大于常规跳频序列的6.777，说明在同一L-G模型下，产生相同频点数的跳频序列，基于附加频移跳频的复杂度大于常规跳频。

3.2 基于Logistic-Kent级联映射构造跳频序列

本文采用文献［1］提出的Logistic-Kent级联映射构造混沌跳频序列。

Logistic映射定义为：

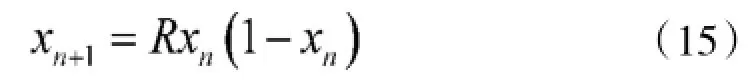
其中，3.75＜R≤4，0＜xn＜1。

Kent映射定义为：

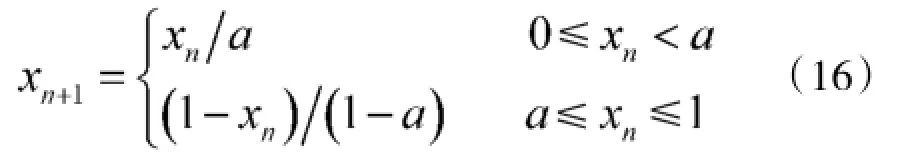
其中，0＜R＜1，0≤xn≤1。构造准则如图11所示。本文中取R=4，a=0.21，x1=0.3，N1=100，N2=1 000则可构造序列长度为100*1 000的混沌时间序列，取不同的M值，则可得到不同频隙数的混沌跳频序列。

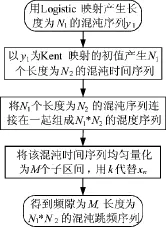
同样取不同的区间数P和区间内频率数q构成256个频点的合成跳频序列，按照3.1节相同的计算流程求取其混沌特征量，其计算值如表2所示。

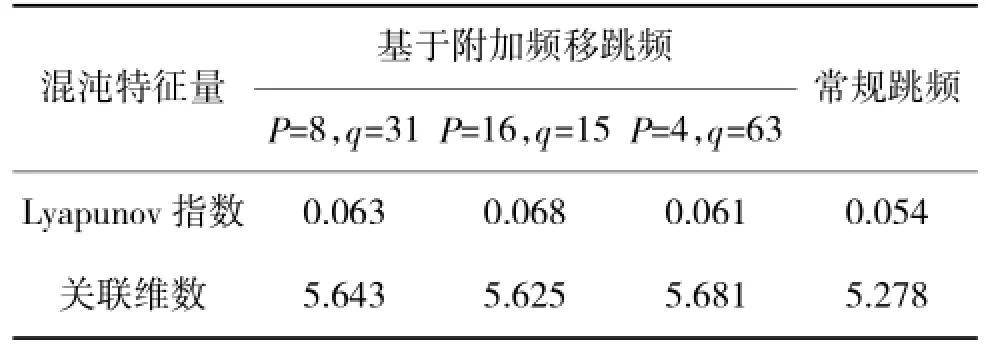
表2 混沌特征量计算值

由表2的混沌特征量计算值可知，基于Logistic-Kent级联映射产生的合成跳频序列和常规跳频序列均具有混沌特性，且基于附加频移跳频3种组合构成的合成序列的关联维数的最小值为5.625，大于常规跳频的5.278，说明在该混沌映射模型下，产生相同频点数的跳频序列，基于附加频移跳频的复杂度大于常规跳频。

4 结论

本文提出一种基于附加频移的跳频方案，通过双序列的控制来提高频率跳变的复杂度，从而增大敌方对于跳频序列的预测难度。通过分析跳频序列的混沌特性，在L-G非连续抽头模型和Logistic-Kent级联映射两类典型模型下，分别计算了基于附加频移跳频和常规跳频两种模式的序列复杂度，其结果表明，在两类典型跳频序列生成模型下，基于附加频移跳频均具有更大的复杂度。

该方案为跳频抗跟踪干扰提供了一种新的参考，但同时应注意到，基于附加频移跳频与常规跳频相比，具有更大的发送和接收处理时延。

［1］李文化，王智顺，何振亚.用于跳频多址通信的混沌跳频码［J］.通信学报，1996，17（6）:17-21.

［2］王喜风，王可人，金虎.基于Tent映射双向耦合映像格子的宽间隔跳频序列及其性能分析［J］.电讯技术，2011，51（5）:17-22.

［3］刘向东，张金海，李志洁，等.基于混沌动态量化的宽间隔跳频序列［J］.电路与系统学报，2010，15（4）:96-100.

［4］马军辉，黄玉清.非重复宽间隔跳频序列的优化［J］.计算机工程与设计，2010，31（4）:3162-3180.

［5］刘思怡.跳频信号预测与混沌同步的研究［D］.成都：电子科技大学，2011.

［6］涂靖.跳频码序列建模与预测研究［D］.成都：电子科技大学，2008.

［7］郭双冰，肖先赐.几种跳频码混沌特性及预测分析［J］.系统工程与电子技术，2000，22（12）:29-32.

［8］陈滨.混沌波形的相关性［M］.西安：西安电子科技大学出版社，2011.

［9］王海燕，卢山.非线性时间序列分析及其应用［M］.北京：科学出版社，2006.

［10］Takens F.On the Numerical Determination of the Dimension of an Attractor.In：Rand D，Young L S editors.Dynamical Systems and Turbulence［M］.Warwick，1980，Lecture Notes in Mathematics，Spring-Verlag，1981，898：366-381.

［11］Wolf A，Swift J B，Swinney H L，et al.Determining Lyapunov Exponents from a Time Series［J］.Physical D，1985（16）：285-317.

［12］Rosenstein M T，Collins J J，De L C.A Practical Method for Calculating Largest Lyapunov Exponents from Small Data Sets［J］.Physical D：Nonlinear Phenomena 1993，65（1-2）：117-134.

［13］Kants H.A Robust Method to Estimate the Maximal Lyapunov Exponent of a Time Series［J］.Physical Letters A. 1994，185（1）：77-87.

［14］Grass B P，Procaccia I.Characterization of Strange Attractors［J］.Physical Review Letters，1983，50（5）：346-349.

［15］Grass B P，Procaccia I.Measuring the Strangeness of Strange Attractors［J］.Physical D，1983（9）：189-208.

［16］梅文华，陈先福.具有最佳汉明相关性能的跳频序列族［J］.国防科技大学学报，1988，10（4）:13-19.

Design of Frequency-hopping Scheme Based on Additional Frequency Shift and Analysis on Its Performance

QUAN Hou-de1，LI Si-qi2，CUI Pei-zhang1，YAN Shi-hao3
（1.Ordnance Engineering College，Shijiazhuang 050003，China；2.Unit 75130 of PLA，Guigang 537000，China；3.Unit 77552 of PLA，Linzhi 860500，China）

To improve the performance of anti-forecasting and enhance the capability of antifollower jamming of Frequency Hopping（FH）system，the FH communication based on additional frequency shift is proposed.In the given FH bandwidth，the complexity of hopped radio frequency is improved under the control of dual-sequence.Thus，this scheme increases the difficulty of modeling and forecasting of FH sequence for enemies.Based on the analysis of chaotic features，the FH complexity is calculated.Compared with the conventional FH system，the results indicate that the FH sequence based on additional frequency shift has greater complexity by the L-G discontinuous tap model and Logistic-Kent cascade mapping.

additional frequency shift，FH sequence，chaotic features，complexity

TN914.41

A

1002-0640（2015）01-0158-05

2013-10-15

：2014-01-27

全厚德（1963-），男，辽宁大连人，博士，教授，博士生导师。研究方向：通信设备性能测试。