导弹飞行试验双方真实风险的确定原则及方法

甄昕

（解放军92941部队，辽宁葫芦岛125000）

导弹飞行试验双方真实风险的确定原则及方法

甄昕

（解放军92941部队，辽宁葫芦岛125000）

长期以来，导弹飞行试验双方风险一直按照规程中规定的方法来确定。采用统计决策理论分析发现以往规程中给出的经典风险和Bayes风险可能存在系统偏差，并给出了修正方法，同时给出了在导弹产品检验中真实风险的确定原则及方法。

经典风险，Bayes风险，简单假设，复合假设

0 引言

从统计决策角度而言，风险就是期望损失。纵观国内外或军内外，在产品抽样检验领域，风险不外乎有两种，一种是经典风险，一种是Bayes风险。

我国海防战术导弹飞行试验主要包括设计定型试验和批抽检试验两大类，无论哪一类试验，其对导弹产品的检验都属于产品抽样检验范畴［1］，都以检验导弹主要质量特性是否满足指标要求来决定导弹产品合格与否。对导弹主要质量特性（一般为单发命中概率）θ的检验主要涉及经典方法和Bayes方法。这些方法体现在已颁布的系列国军标中，包括各类导弹武器系统设计定型规程（例如从1994年颁布的GJBZ20217-94到2009年颁布的GJB6671-2009）和导弹制导精度评定规程等，它们规定了导弹主要质量特性的各种检验方案。数十年来导弹飞行试验一直遵照规程执行，但不论是用经典还是Bayes检验方法，为了体现试验的合理性、公平性，通常采用“风险相当”的原则来制定产品检验方案［2］，所以试验双方风险的确定成为至关重要的因素。

1 问题分析

长久以来，对导弹等昂贵军品的检验，一般采用一次计数或二次计数抽样检验方案、计数序贯概率比假设检验方案等［3］。无论采用哪种检验方案，根据产品质量抽样检验理论，试验前需要确定4个数，即生产方风险α、生产方风险质量（也称可接受质量）θ0、使用方风险β、使用方风险质量（也称极限质量）θ1［4］。当θ≥θ0时，产品合格；当θ≤θ1时，产品不合格。

在产品检验过程中，设有统计假设：

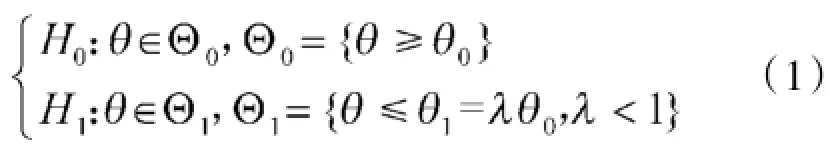
经典风险α和β一般被表示为：

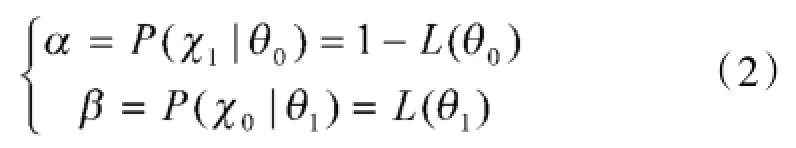
其中，χ0和χ1分别为接受和拒收产品的子样空间，L（θ）为接收概率。

Bayes风险απ和βπ一般被表示为（这也是规程中给出的风险表达式［2］）：

其中，π0、π1分别为θ=θ0和θ=θ1时的先验概率。

对于经典方法而言，在试验前明确α和β，是为了使抽样特性曲线即OC曲线通过两个指定点，即有式（2）成立，所以α和β是“指定风险”，非试验前双方所冒真正风险或期望风险，但是在国军标中采用原假设和对立假设均为简单假设的形式［2］，并规定Θ=Θ0+Θ1，且用式（2）计算双方在试验前的“真实风险”。

在产品质量抽样检验过程中，只有当Θ≠Θ0+Θ1时，统计假设（1）才与实际情况相符，设Θ2=（θ1，θ0），则有Θ=Θ0+Θ1+Θ2，那么式（2）给出的风险公式没有考虑θ∈Θ2时的情况，使经典风险的计算可能存在系统偏差。

2 “真实风险”的确定方法与风险确定原则

根据统计决策理论［5］，经典风险R（θ，a）为：

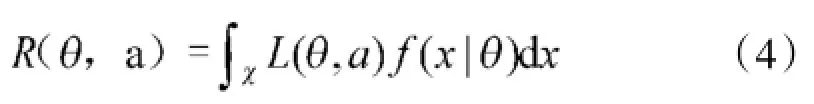
其中，χ为产品子样空间，L（θ，a）为损失函数，f（x|θ）为似然函数。

从产品检验中双方所冒风险或遭受损失角度而言，产品质量的合格标准是“唯一”的，即当θ≥θ0时产品检验结果合格接收此批产品，则此决策对使用方而言是没有风险或损失的；当θ＜θ0时产品检验结果不合格拒收此批产品，则此决策对生产方而言是没有风险或损失的，反之都是有风险或损失的。风险或损失正是由于非全额检验造成的。据此，在制定检验方案时取0-1损失函数［6］，有：

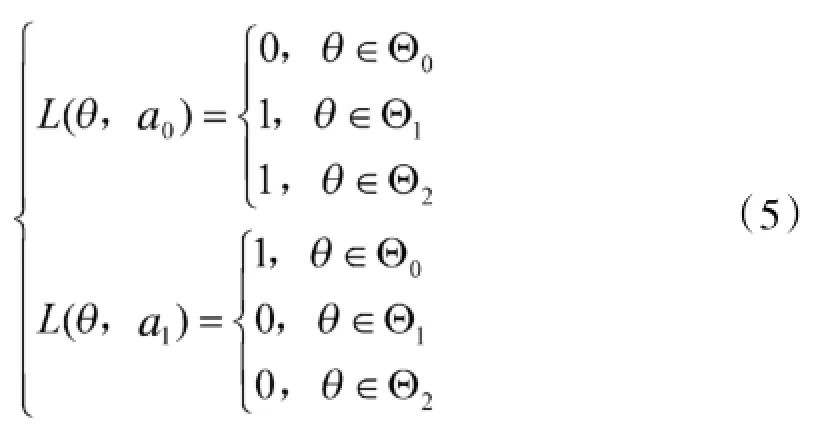
其中，a0：接收假设H0，a1：接收假设H1。

将式（5）代入式（4），可得到“真实”经典风险α'与β'公式：

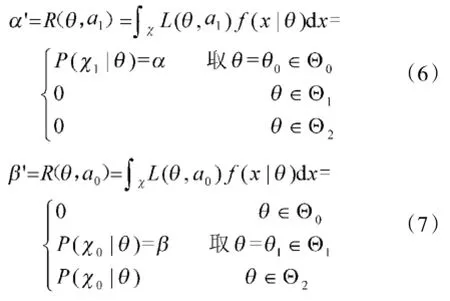
由式（6）、式（7）可得：

（1）当θ∈Θ，α'=α；当θ∈Θ0或θ∈Θ1时，β'=β。

（2）当θ∈Θ2，因β无值或者按θ=θ1来计算β，有β'＞β。

从以上两点可以看出：“真实风险”α'和β'是否与”指定风险”α和β相同，取决于产品质量θ，如果产品质量不好也不差即θ∈（θ1，θ0）时，“真实”使用方风险β'要大于、有时要远远大于“指定”的生产方风险β。无论是用什么方法来制定产品抽样检验方案，以上结论均成立。

目前已颁布的有关海防战术导弹设计定型试验的系列国军标中，有关风险的计算均未考虑θ∈（θ1，θ0）时的情况，致使“真实”使用方风险有可能增大，由于一直以来在制定导弹主要指标检验方案时，都是坚持双方风险相当的原则，其结果是使检验的评定标准（核心是几发几中问题）可能有利于生产方，而不利于使用方（见案例分析）。

产品抽样检验中“真实风险”与“指定风险”的关系是由产品质量θ决定的，而θ在试验前处于什么状态通常是不确知的（对于设计定型的导弹产品尤其如此），或者可以理解为其取值是随机的，那么用Bayes风险来取代经典风险应该是合理的。

通过以上分析，可知规程中给出的Bayes风险απ和βπ即式（3）可能同样存在系统偏差。

根据统计决策理论［5］，Bayes风险r（θ，a）由式（8）决定：

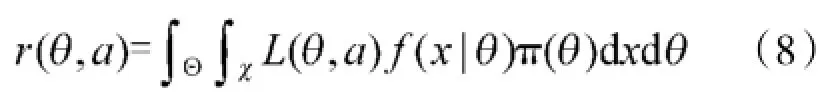
其中，π（θ）为θ的先验概率密度函数。

将式（5）代入式（8），可得到Bayes“真实风险”απ'与βπ'公式：

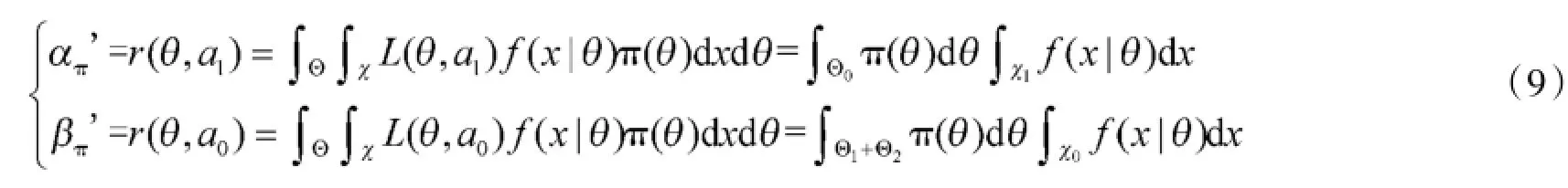
通过以上分析并结合笔者在导弹飞行试验与鉴定领域的工作经验，建议在产品抽样检验过程中，采取以下确定风险的原则：

（1）采用经典方法制定检验方案，应使“真实风险”和“指定风险”相一致，即在选取θ0、θ1时，避免出现产品子样的质量状态θ∈（θ1，θ0）的情况。

（2）采用Bayes方法制定检验方案，双方的Bayes风险按式（9）计算，此时，采用原假设和对立假设均为简单假设的方式是不可取的，应采用原假设和备择假设均为复合假设的方式，如式（1）。

（3）无法确知θ∉（θ1，θ0）时，建议采用（2）原则；如果坚持采用经典方法，建议在实际操作中，在由“指定风险”确定的抽样检验方案基础上适当加大抽验量，以减小使用方的“真实风险”。

3 案例分析

采用GJB6671-2009给出的范例。假设某型导弹设计定型试验，对其单发命中概率θ检验的统计假设为：H0：θ0=0.75，H1：θ1=0.58，且有导弹研制试验结果作为先验信息（n0，s0）=（8，6），利用简单假设Bayes检验方法制定的检验方案为（sn，fn）=（5，2），即定型试验7发5中合格，经计算双方风险απ=0.1510、βπ=0.140 9，基本相当。试根据以上数据制定形如式（1）的复合假设Bayes检验方案，并比较两方案的Bayes风险。

解：设复合假设如式（1）所示，且有θ0=0.75，θ1= 0.58。取导弹试验样本量n=6、7、8，根据子样后验概率似然比，分别得到相应的检验方案（sn，fn），并利用式（9）计算Bayes风险απ'、βπ'，结果见表1。本案例用Matlab编程计算，计算过程中的积分值由int（）函数求取。

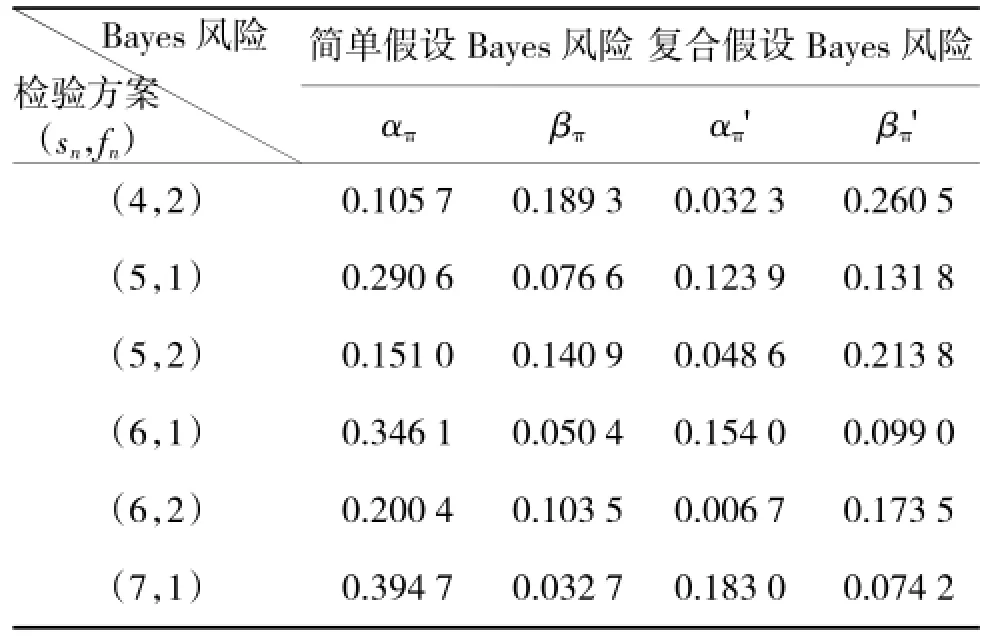
表1 导弹单发命中概率两种检验方案Bayes风险比较

从表1可知：

（1）对于表中给出的6个检验方案，在复合假设Bayes检验方法下，用式（9）计算得出的Bayes风险βπ'均大于相应的规程方法，即式（3）计算得出的Bayes风险βπ。

（2）按照双方Bayes风险相当的原则，规程中给出的检验方案为（sn，fn）=（5，2），即定型试验7发5中合格；用复合假设Bayes检验方法选择的检验方案为（sn，fn）=（5，1），即定型试验6发5中合格。

所以从Bayes风险或试验公平性角度而言，用以往规程给出的简单假设Bayes检验方法来制定检验方案，相比较用复合假设Bayes检验方法来制定检验方案，“人为”地减小了使用方Bayes“真实风险”，使检验方案有利于生产方，照顾了生产方利益，但损害了使用方利益。

4 结论

在导弹飞行试验与鉴定中，由以往规程给出双方风险应为“指定风险”，与试验时双方所冒的“真实风险”特别是使用方Bayes风险存在偏差，所以在制定导弹可靠性指标检验方案时，建议采用文中给出的原则和方法。

文中给出的“真实风险”确定原则及方法，适用于作为“孤立批”检验的军品，同时对于作为“孤立批”检验的民品也有重要的参考和借鉴意义。

［1］何国伟.可靠性试验技术［M］.北京：国防工业出版社，1995：56-57.

［2］李守秀.GJB 6671-2009反舰导弹定型试验规程［S］.北京：中国人民解放军总装备部，2009:15.

［3］茆诗松王玲玲.可靠性统计［M］.南京：华东师范大学出版社，1985：220-221.

［4］马毅林，于振凡.产品质量抽样检验［M］.北京：中国标准出版社，1997：33-36.

［5］James O B.Statistical Decision Theory and Bayesian Analysis［M］.New York：SVNY Publishing，1980：11-109.

［6］王正明，卢云芳.导弹试验的设计与评估［M］.北京：科学出版社，2010：50.

Principles and Methods about the Real Risk of Both Sides in the Flying Test of Missiles

ZHEN Xin
（Unit 92941 of PLA，Huludao 125000，China）

The risk on both sides in the flying test of missiles has been fixxed using the methods stipulated by the criteria.It is found that there is some possible system errors during calculating the classical risk and Bayes risk given by the past criteria through adopting statistical decision theory in this article.Meantime，the relatively correct methods has been vindicated.The principle for determining the risk in the inspection of products has been given at last.

classical risk，Bayesian risk，a point hypothesis，a complex hypothesis

TJ760.6+2

A

1002-0640（2015）01-0167-03

2013-10-10

2014-01-28

甄昕（1970-），男，河北无极人，高级工程师。研究方向：导弹武器系统试验与鉴定总体技术。