Duffing系统线谱值降低的参数选取

兰朝凤，陈 欢，张 梦，李凤臣

(1.哈尔滨理工大学电气与电子工程学院，黑龙江 哈尔滨 150080;2.哈尔滨工业大学 能源科学与工程学院，黑龙江 哈尔滨 150001;3.中国舰船研究设计中心，湖北武汉 430026)

混沌是非线性科学的一个重要分支，是美国气象学家E.N.Lorenz在1963年研究大气运动对流试验时，首次发现的流体的一种特殊运动形式.混沌理论作为非线性科学的重要分支，有人预言它将主导21世纪的科学，同时，自然界中的混沌现象几乎是无处不在.混沌现已被广泛应用于物理学、数学、流体力学、化学、生物学、信息科学、医学、经济学及社会科学等各个领域，而在各个领域中的应用也各有特点［1-6］.

近年来，随着混沌理论的深入研究，混沌控制与反控制技术取得了长足进步，20世纪90年代取得了重要突破，提出了混沌控制及反控制的方法:实现混沌的首要条件是建立对初始条件的敏感性;改变系统参数;引入外部扰动;非线性是系统出现混沌的必要条件，也就是说混沌是非线性系统的通有行为.那么，对于一个系统来说，如何设计系统参数，才可以使系统出现混沌或避免混沌现象的出现，这就涉及到怎样控制系统参数或外激励参数来实现定态到混沌或从混沌到定态的过渡过程［7］.因此，针对非线性动力学系统开展混沌机理、系统动力学运动规律的研究显得具有重要的理论意义和实际应用价值.

目前混沌处理方法被应用到各个领域，如极具代表性的Duffing方程应用到非线性隔振系统、船的横摇运动、结构振动、微弱周期信号检测、电力系统周期振荡分析、周期电路系统的模拟与控制等的分析中［8-10］，它描述了系统的共振现象、调和次调和振动、拟周期振动、混沌现象等.对于系统中复杂的运动形式，如何选取参数以使得系统处于平衡状态、周期运动、拟周期运动、混沌运动非常重要，因此，文中详细探讨系统的阻尼参数、非线性参数、外激励参数对系统输出动力学规律的影响以及输出功率谱值的变化规律，为实际工程应用提供一定的参考.

1 Duffing系统的动力学模型

单自由度Duffing振子是描述系统共振、调和、次调和振动、拟周期振动以及混沌现象的最简单数学模型，因此，对它进行参数分析可以解释一类相似的动力学问题.模型形式为

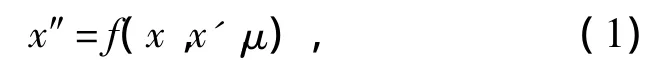
式中:x为状态变量;f(x，x'，μ)为向量场，是一广义函数;μ为系统可调节参数.

外力作用下的硬弹簧Duffing振子的振动形式为

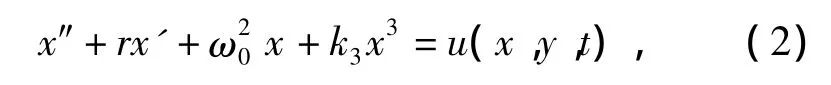
式中:r为系统阻尼参数;ω0为系统固有振动角频率;k3为系统非线性恢复力参数;u(x，y，t)为外部控制器.

式(2)写为广义状态方程的形式为

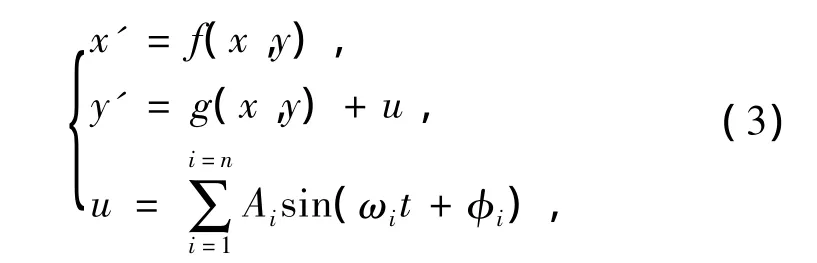
式中:f(x，y)和g(x，y)均为广义函数的形式;A和ω为施加外激励的幅值和角频率;φi为相位角;i代表施加外激励的个数，为正整数.

当式(3)中为单频外激励时，式(3)可写为以下形式的状态方程:

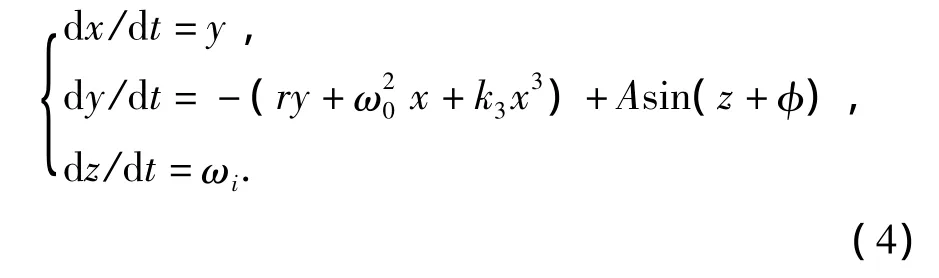
为分析线性系统、非线性系统、外激励作用下的非线性系特征，以及系统参数与外激励参数对系统输出功率谱的影响，进行数值分析.

本文目的在于通过系统参数的有效控制，实现混沌信号的输出，进而实现信号能量的降低.

2 数值分析

根据已有的研究可知，Duffing系统未受外激励扰动时，处于自激振荡状态，由于自身存在阻尼的影响，经过一段时间后系统输出接近于0，最终处于稳定状态;在相平面图上表现为一条孤立的封闭曲线，即极限环;功率谱类似于噪声谱;Poincare截面是处于混沌输出状态的乱点，但是仍然是一个圆环，可以判定系统处于拟周期运动状态.由此分析，要想使系统最终处于稳定的动力学运动状态，需对该非线性自激振动系统施加外激励以维持系统的运动轨迹.以下仿真研究不同的外激励作用于系统和系统参数改变时，系统输出的动力学特征.

2.1 非线性参数对系统输出特性的影响

仿真参数:外激励幅值A=50.00 N，角频率ω=1.000 rad·s-1，系统谐振角频率 ω0=1.000 rad·s-1(全文仿真中此参数均取此值)，阻尼系数r=0.250 0.系统输出随非线性参数k3变化的分岔图如图1所示;非线性参数k3的取值范围为0.100 0～1.000 0，等间隔变化.

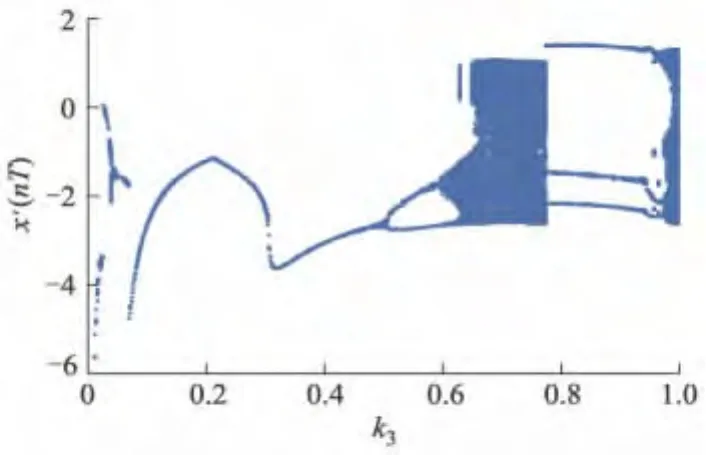
图1 输出随非线性参数变化的全局分岔图

由图1可知，非线性参数取0.200 0，0.510 0，0.600 0与1.000 0时，系统输出分别处于周期一运动、周期二运动、周期四运动与混沌运动状态.系统输出的最大LE(Lyapunov指数的简写)Lmax与非线性参数k3的关系曲线如图2所示.

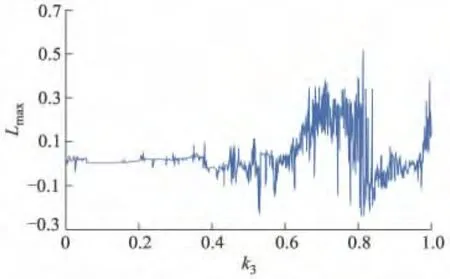
图2 随非线性参数k3的最大LE曲线

由图2可知，非线性参数区间为0.627 6＜k3＜0.805 8，系统输出的最大LE除少数点小于0外，其他参数处取值均大于0，表明系统处于混沌运动状态.非线性参数k3=0.813 8时LE最大，为0.512 3，表明此参数处混沌程度最强.

2.2 阻尼参数对系统输出特性的影响

仿真参数:非线性参数k3=1.000 0，外激励幅值A=50.00 N，角频率ω=1.000 rad·s-1.系统输出随阻尼参数r变化的分岔图如图3所示.

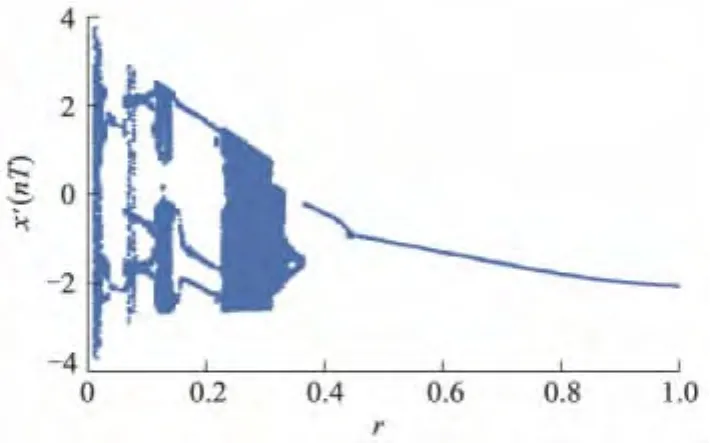
图3 输出随阻尼参数r变化的全局分岔图

由图3可知，在r=0.420 0处发生了一次逆倍周期分岔，r=0.360 0发生第2次逆分岔，即r在区间(0.420 0，1.000 0)中系统处于周期一运动，在区间(0.360 0，0.420 0)中系统处于周期二运动;平面上有无限个混乱的点代表系统发生混沌，即r在区间(0.200 0，0.320 0)中系统处于混沌状态.

仿真参数:外激励幅值A为50.00 N，角频率为1.000 rad·s-1，阻尼参数r为0.250 0，非线性系数k3为 1.000 0，阻尼系数r的取值范围为 0～1.000 0，等间隔变化.系统输出的最大LE与阻尼参数r的关系曲线如图4所示.

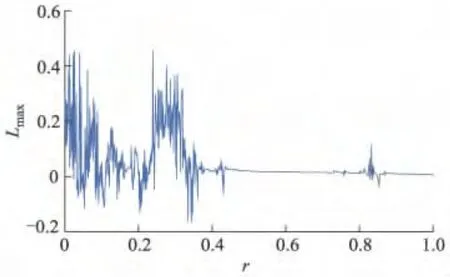
图4 最大LE与阻尼参数的关系

由图4可知，阻尼参数r＞0.460 0时，系统输出的最大LE接近于0，表明系统的混沌程度较弱;当阻尼系数在0.243 2＜r＜0.305 3及0.434 4＜r＜0.829 8区间时，系统输出的最大LE大于0，表明系统处于混沌运动状态;当r=0.239 2时，系统输出的最大LE为0.451 6，系统混沌程度最强.由此，据系统输出的最大LE大小，可选定系统所处混沌程度强弱的阻尼参数.

2.3 外激励幅值与角频率参数对系统输出特性的影响

仿真参数:非线性参数k3=1.000 0，阻尼参数r=0.250 0，外激励幅值从0.10～100.00 N，以0.1为步长变化，角频率以步长0.1变化，系统输出LE大于0时的外激励幅值和角频率参数值利用描点法在图上绘出，如图5所示.

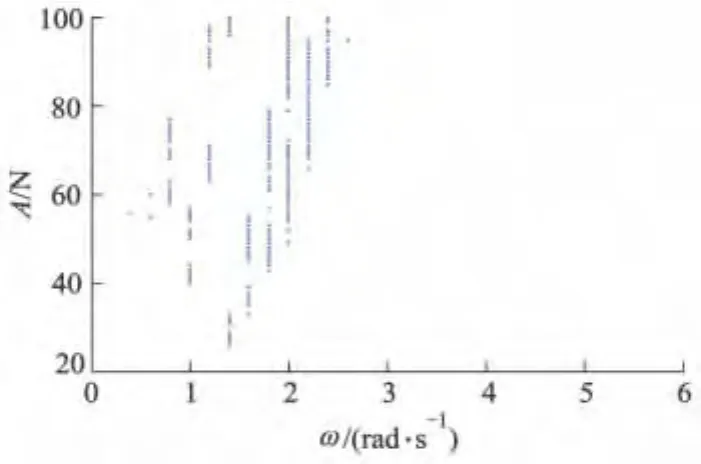
图5 输出LE随A和ω变化的混沌区域图

图5可实现外激励幅值和角频率的混沌区域参数的联合选取.

仿真参数:阻尼参数r为0.250 0，非线性参数k3为1.000 0，外激励角频率ω为1.000 rad·s-1，幅值A的取值范围是0～100.00 N，等间隔变化.系统输出的最大LE与A关系曲线如图6a所示.外激励幅值为50.00 N，角频率ω的取值范围为0～20.000 rad·s-1，等间隔变化.系统输出的最大LE与ω关系曲线如图6b所示.

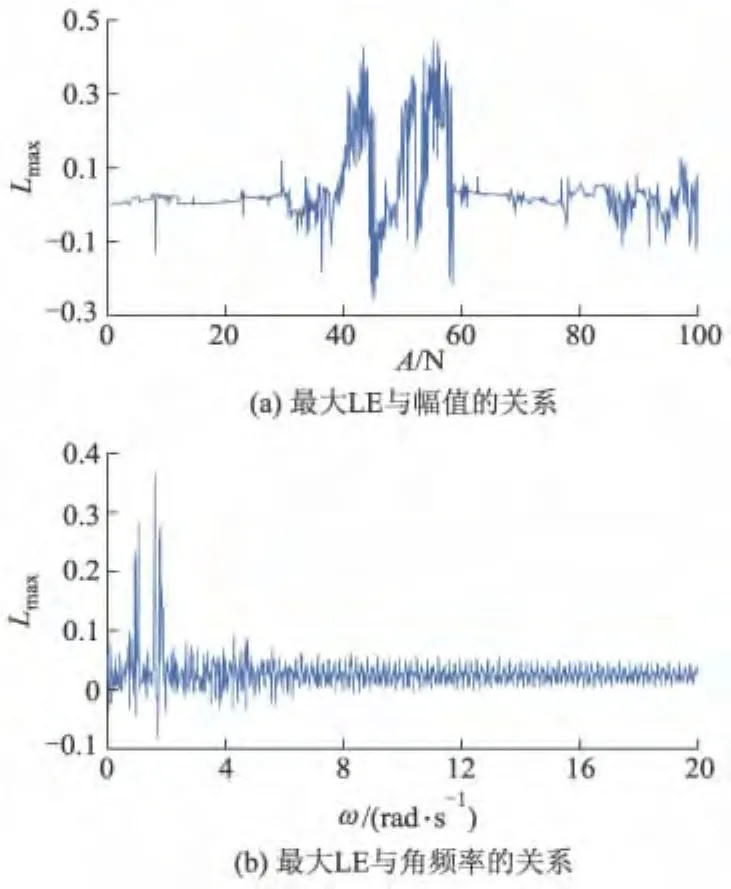
图6 最大LE与A，ω的关系

由图6a可知，当外激励幅值在38.94 N＜A＜44.44 N与53.15 N＜A＜57.66 N区间时，系统输出的最大LE较大.外激励幅值A=55.16 N时，系统输出的LE最大，为0.439 4，此幅值处系统所处混沌程度最强.由图6b可知，外激励角频率在1.702 rad·s-1＜ω ＜2.002 rad·s-1与0.901 rad·s-1＜ω＜1.201 rad·s-1区间时，系统输出的最大LE较大.当角频率ω=1.802 rad·s-1时，系统输出的LE最大，为0.390 3，此角频率处系统所处混沌程度最强.由此表明，据系统输出的最大LE大小，可选取系统所处混沌程度强弱的幅值参数和角频率参数.

2.4 功率谱下降值的数学统计表

根据2.2与2.3节的数值分析结果，选取一些代表性的参数，给出系统输出的基频处功率谱与线性系统基频处功率谱的差值及系统运动状态.表1中外激励角频率ω=1.000 rad·s-1.

对单自由度Duffing系统，调节系统阻尼参数、非线性参数及外激励参数均可改变系统的运动状态，即系统参数与外激励参数共同作用、相互制约着系统的运动规律.通过适当调整控制参数，实现混沌反控制，有望控制系统稳定地处于混沌运动状态，输出线谱值降低，提高隔振效果.

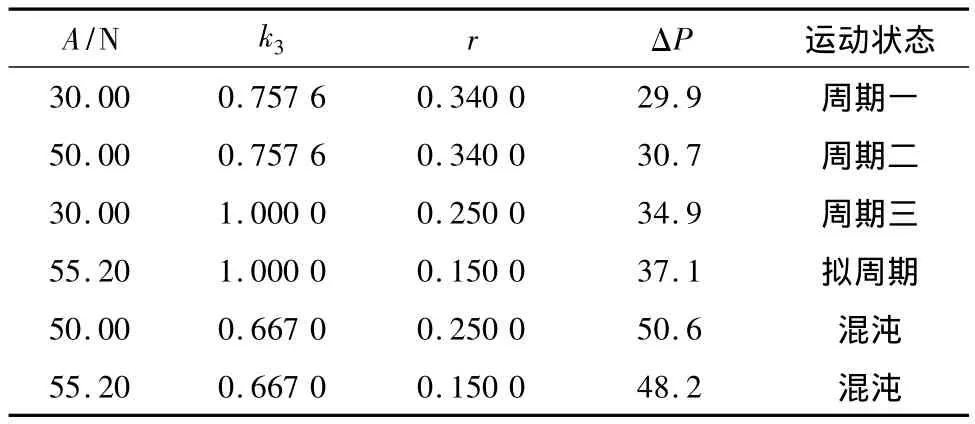
表1 系统输出功率谱值的统计表

3 结论

1)系统具有非线性是系统发生混沌运动的必要条件，非线性系数越小，系统越难发生混沌.

2)系统阻尼参数越小，到达混沌所需的激励力越小，混沌区域分布在更大的参数平面内.

3)在一定范围内，外界的激励力幅值A越大、激励角频率 ω越小，系统发生混沌的可能性就越大.

4)系统混沌运动的产生是系统阻尼参数、非线性参数、外激励参数之间是共同作用、相互制约的结果.适当调整控制参数，实现混沌反控制，有望控制系统稳定地处于混沌运动状态，达到降低单频线谱值的目的.

References)

［1］王树国，姚洪兴.拓扑结构时变的多时滞耦合供应链复杂网络的牵制控制［J］.江苏大学学报:自然科学版，2012，33(2):239-243.

Wang Shuguo，Yao Hongxing.Pinning synchronization of supply chain complex networks with time-varying topological structures and multiple coupling delays［J］.Journal of Jiangsu University:Natural Science Edition，2012，33(2):239-243.(in Chinese)

［2］余 跃，张 春，毕勤胜.非线性切换系统的振荡行为及其Lyapunov指数计算［J］.江苏大学学报:自然科学版，2014，35(5):611-615.

Yu Yue，Zhang Chun，Bi Qinsheng.Oscillated behavior and Lyapunov exponent calculation of nonlinear switching system［J］.Journal of Jiangsu University:Natural Science Edition，2014，35(5):611-615.(in Chinese)

［3］刘海波，吴德伟，戴传金，等.基于Duffing振子的弱正弦信号检测方法研究［J］.电子学报，2013，41(1):8-12.

Liu Haibo，Wu Dewei，Dai Chuanjin，et al.A new weak sinusoidal signal detection method based on Duffing oscillators［J］.Acta Electronica Sinica，2013，41(1):8-12.(in Chinese)

［4］邓冬虎，张 群，罗 迎，等.Duffing振子在低信噪比雷达目标微动特征提取中的应用［J］.电子与信息学报，2014，36(2):453-458.

Deng Donghu，Zhang Qun，Luo Ying，et al.The application of Duffing oscillators to micro-motion feature extraction of radar target under low SNR［J］.Journal of E-lectronics＆Information Technology，2014，36(2):453-458.(in Chinese)

［5］Shoghi Rahim，Tabeshpour Mohammad Reza.An approximate method for the surge response of the tension leg platform［J］.Journal of Marine Science and Application，2014，13:99-104.

［6］He Guitian，Luo Maokang.Dynamic behavior of fractional order Duffing chaotic system and its synchronization via singly active control［J］.Applied Mathematics and Mechanics:English Edition，2012，33(5):567-582.

［7］Liu Bin，Zhou Yiming，Jiang Min，et al.Synchronizing chaotic systems using control based on tridiagonal structure［J］.Chaos，Solitons and Fractals，2009，39:2274-2281.

［8］杨红英，葛传虎，叶 昊，等.基于Duffing振子的天然气管道泄漏检测方法［J］.高技术通讯，2010，20(6):628-631.

Yang Hongying，Ge Chuanhu，Ye Hao，et al.Leak detection based on Duffing oscillators for gas pipelines［J］.Chinese High Technology Letters，2010，20(6):628-631.(in Chinese)

［9］罗文亮，柯熙政，李 欣.电力载波通信中强背景噪声下弱信号的混沌振子检测方法［J］.量子电子学报，2010，27(2):134-139.

Luo Wenliang，Ke Xizheng，Li Xin.Chaotic oscillator detection methods of weak signal in strong background noise of power line communication［J］.Chinese Journal of Quantum Electronics，2010，27(2):134-139.(in Chinese)

［10］Yuan Peixin，Li Yongqiang.Approximate solutions of primary resonance for forced Duffing equation by means of the homotopy analysis method［J］.Chinese Journal of Mechanical Engineering，2011，24(3):501-506.