螺旋桨流固耦合特性的数值模拟

孙海涛，熊 鹰，时立攀

(1.国防科学技术大学指挥军官基础教育学院，湖南长沙 410072;2.海军工程大学舰船工程系，湖北武汉 430033)

螺旋桨通常采用金属材料制作，其设计和性能预报在刚性假设基础上进行，不考虑结构变形的影响.但对于具有较大侧斜角的螺旋桨或采用复合材料制作的螺旋桨，弹性的增加引起变形增大.变形后的螺旋桨将影响周围流场及其承受的水动力载荷，变化后的载荷又将影响桨的变形，这是流体与结构相互作用的问题.此种情况下，桨叶变形对螺旋桨性能的影响不可忽略.

弹性变形桨的数值计算最早出现于1991年，文献［1］采用涡格法计算了水下无空泡螺旋桨的定常水动力性能，并利用有限元软件 ABAQUS进行应力分析，未考虑流体结构的相互作用.文献［2-7］在后来的研究中，针对复合材料螺旋桨耦合变形的特点改进上述方法，将涡格法计算程序与ABAQUS联合迭代求解，并进行了强度评估和模型试验研究，研究表明:材料纤维及铺层设计对螺旋桨变形和性能有显著影响，但仅靠改变纤维铺层方式难以最大限度地发挥复合材料螺旋桨的优势，须配合调整螺旋桨的外形，进行预变形设计.文献［8］以燃料消耗最小化为目标进行纤维的铺层优化设计，采用边界元法与ANSYS软件对设计结果进行耦合计算.文献［9-12］将边界元法与有限元法结合起来，建立了流固耦合算法，并研究了桨叶变形特性及变形对水动力性能的影响.流体部分采用基于速度势的低阶面元法，运用Newton-Raphson方法对格林第3公式进行离散求解，得出桨叶面元的速度势进而求得螺旋桨水动力性能及桨叶表面压力分布.结构部分利用ABAQUS软件的二次开发功能，编写实体单元的生成程序和水动力载荷的加载程序，以实现流体面元与结构单元表面的对应和载荷的正确加载.得到节点位移之后，将其导入流体计算程序以更新面元节点信息进行新的求解.文献［13-16］在复合材料螺旋桨的流固耦合算法方面进行了大量的研究，建立了较为完善的流固耦合控制方程和求解算法，给出了复合材料螺旋桨预变形设计的原则.

上述数值算法在求解螺旋桨水动力载荷时，均采用基于流体为无黏假定的势流方法.随着计算机技术的发展，基于雷诺时均Navier-Stokes方程的计算流体力学方法(CFD)逐渐成为一种预报螺旋桨性能的新兴方法［17］，该方法综合考虑了流体黏性和旋度等因素的影响，使获得螺旋桨黏性流场的全场信息成为可能.笔者采用求解RANS方程的方法对螺旋桨3维流场进行模拟，利用有限元方法计算螺旋桨结构响应，结合ANSYS软件中的流体载荷和结构响应数据实时双向传输技术，对螺旋桨进行流固耦合特性分析.

1 数值方法

RANS方程是黏性流体运动学和动力学的普适性方程，与连续性方程一起构成流体控制方程，将其作为求解螺旋桨水动力性能的基本方程.RANS方程是通过将瞬时N-S方程中的速度、压强、质量力和密度等流体变量进行时历平均化后得到，其形式如下:

式中:ρ为流体密度;ui，uj，ul为速度分量;p0为静压;fi为单位质量力.

桨叶在外载荷作用下将产生弯扭耦合变形，对其运动学方程进行有限元离散可得有限元方程:

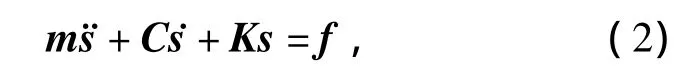
桨叶质量可由密度和外形等确定，刚度可由弹性模量和泊松比确定.桨叶结构阻尼较难计算，通常将其简化为质量矩阵和刚度矩阵的线性组合.

流场计算采用ANSYS中的CFX求解器，结构响应计算采用ANSYS中的结构有限元求解器.为实现流场与结构响应计算数据的实时双向传递，将有限元求解器的设置输出为结构求解程序，形成CFX可接受的INP文件，而后在CFX的分析类型中打开外部求解器功能，选择ANSYS多场分析并读入生成的结构求解程序.这样做的优势:可以充分发挥流体计算与结构计算的已有经验，并且所有流体与结构的分析结果都将保存在流体模块的结果文件中，便于查看.双向流固耦合分析的设置相对较为复杂，设置不合理将导致计算的中断，主要集中的问题:① 流体分析与结构分析的时间步必须统一;②结构变形导致的流场网格问题，需要采用网格移动技术方可模拟变形对流场的影响.

2 网格划分

若要求解较为准确的流场信息，就需要在计算域中划分出能正确反映螺旋桨边界形状且具有一定分辨率的计算网格.螺旋桨几何形状复杂，叶面呈螺旋状扭曲结构，桨叶剖面沿半径方向先逐渐扩大而后急剧收缩，对其流场划分结构化网格十分困难.并且结构化网格以六面体网格为基础，即使设法对包含有螺旋桨这样复杂几何形状的计算域进行了结构化网格划分，也会产生大量质量较差的扭曲网格，影响计算的速度和精度，而非结构网格就可以避免这一问题.非结构化网格以四面体为基础，对网格结点没有严格的限制，比较适用于像螺旋桨流场这样边界几何形状复杂的计算域，但非结构化网格的不足在于同等网格尺度条件下填充率较低，所需要的网格数量较大.

以HG5-1螺旋桨为研究对象，模型直径D为240 mm，将计算域分为圆柱形的固定域和旋转域.外圆柱体区域直径为9.0D，入口取在螺旋桨上游3.0D处，出口取在下游7.0D处.内圆柱体区域直径为1.5D，入口取在螺旋桨上游0.8D处，出口取在下游1.2D处.内部旋转域采用单旋转系模型对螺旋桨的旋转流场进行求解.这种模型是建立一个固连于螺旋桨的旋转坐标系，并将螺旋桨周围的流域独立出来，从而使得这个流域的流场在旋转坐标系下是定常的，而这个流域之外的流域在绝对静止坐标系下也可以近似认为是定常的.为降低总体计算网格的数量，采用结构化-非结构化多块混合网格划分方法，即对紧邻于螺旋桨的形状复杂流域进行非结构化网格划分，如图1，2所示.

图1 螺旋桨表面的非结构化网格

图2 流场内域的非结构化网格

为弥补非结构网格填充率较低的不足，对螺旋桨流场的外域，划分高质量的结构化网格，流场计算域的总网格数为150.0万个，如图3所示.桨叶变形计算时，采用四面体单元对其进行有限元剖分，总单元数为2.9万个，如图4所示.

图3 流场外域的结构化网格

图4 螺旋桨有限元网格

3 结果与分析

螺旋桨转速设为900 r·min-1，通过变化进流速度大小来改变进速系数.螺旋桨材料为铜合金，其杨氏模量为110 GPa，泊松比为0.34，密度为8 300 kg·m-3.为进行比较分析，增加螺旋桨的弹性，将材料的杨氏模量降为15 GPa，密度设为1 500 kg·m-3，其他参数保持不变.记弹性增加后的桨为弹性桨，铜合金桨为刚性桨.流固耦合面设为桨叶表面，数据即在此面上交换传递.

刚性桨水动力性能的预报值与试验值的比较如图5所示，KF，KM，η分别为弹性桨的推力系数、转矩系数和效率，由于变形较小，考虑结构变形影响与否的水动力性能变化甚微，均与试验结果较为接近.因而，对常规金属桨进行性能预报时，可以不考虑流固耦合的影响.而弹性桨的情况则不同，弹性的增加使得变形增大，进而对周围流场产生影响.弹性桨与刚性桨预报值比较如图6所示，考虑变形的影响后，弹性桨的推力和转矩均比刚性桨小.在低进速时，由于转矩小更多，效率略高于刚性桨.高进速时，推力减小更多，效率略低于刚性桨.进速系数J=0.5时，弹性桨的最大变形为0.81 mm，而刚性桨的最大变形仅为0.11 mm;弹性桨的最大应变为1.03×10-3，刚性桨的最大应变为1.42×10-4;弹性桨的最大等效应力为11.03 MPa，刚性桨的最大等效应力为11.16 MPa.对于弹性桨而言，桨叶变形不仅影响水动力性能，还将引起桨叶几何参数的变化，进而导致整个运转状态及流场的改变.在这种情况下，考虑流固耦合的影响是很有必要的.

图5 水动力性能预报值与试验值的比较

图6 弹性桨与刚性桨预报值的比较

不同工况下，弹性桨与刚性桨的结构响应特性对比如图7所示，Δsmax为最大位移，σmax为最大应力，εmax为最大应变.随着进速系数降低，螺旋桨承受的载荷增加，变形及应力应变随之增加.在进速系数相同时，弹性桨的最大变形及应变明显高于刚性桨，而最大等效应力略低于刚性桨.可见，材料特性对变形和应变的影响是显著的.而应力则是表示单位面积上的受力，在螺旋桨载荷未发生明显变化的情况下，其变化范围较小.前面的计算显示，弹性桨承受的载荷较刚性桨为小，因而其最大等效应力亦略小于刚性桨.

最大结构响应从宏观上反映了螺旋桨运转时的情况，在强度评估与分析时，往往需要研究更为细致的应力应变分布.2种材料螺旋桨在J=0.5时的结构响应云图如图8所示，桨叶最大变形出现在叶梢，变形量从叶梢到叶根依次递减，类似于悬臂梁受力后的变形特性.设R为螺旋桨半径，在(0.6～0.7)R之间出现了明显的应力集中，最小值则位于叶梢和叶根随边部位.应变的分布规律与等效应力相近，因为二者的相差仅在于弹性矩阵.

图9，10分别为桨叶压力分布和尾流的计算结果，其分布规律相似，从图中难以看出区别.具体数值上，弹性桨压力的负压峰值增加，正压峰值降低，叶面和叶背的压力差减小.从流线分布情况可知:尾涡半径有一定的收缩，反映了螺旋桨对流体的抽吸作用.

图11，12分别为螺旋桨在J=0.5时不同断面处压力分布和涡量分布的计算结果，图11a，d，图12a，d 为盘面上游 0.20D位置，图 11b，e，图 12 b，e为盘面位置，图 11c，f，图 12 c，f为盘面 下游0.15D位置.涡量幅值和压力在盘面处最大，下游断面次之.弹性桨的涡量幅值和压力在盘面处的增加，上游与下游断面有所降低，分布形式无明显区别.

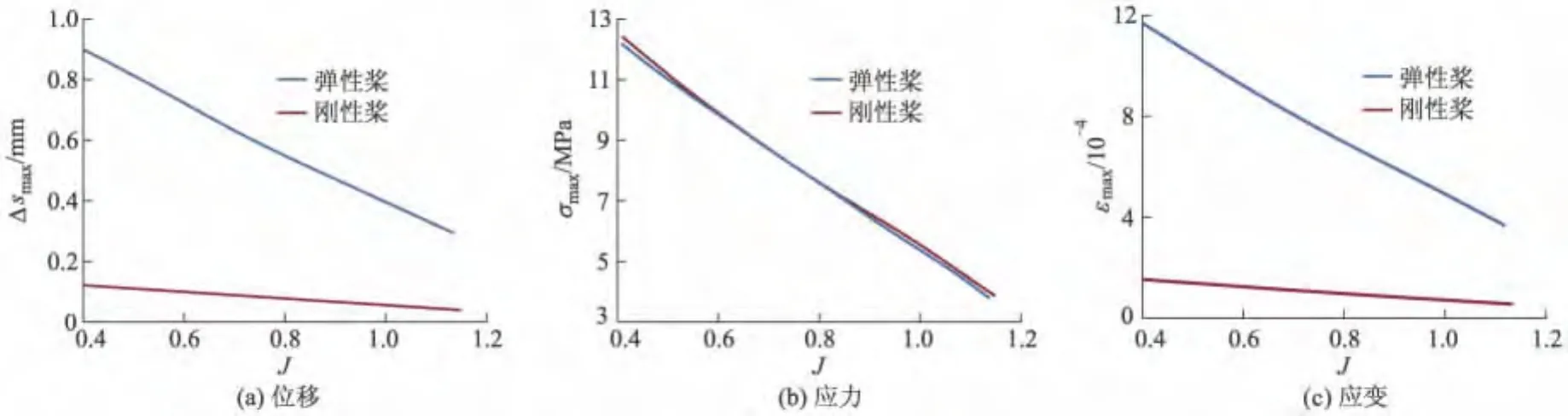
图7 弹性桨与刚性桨位移、应力及应变比较

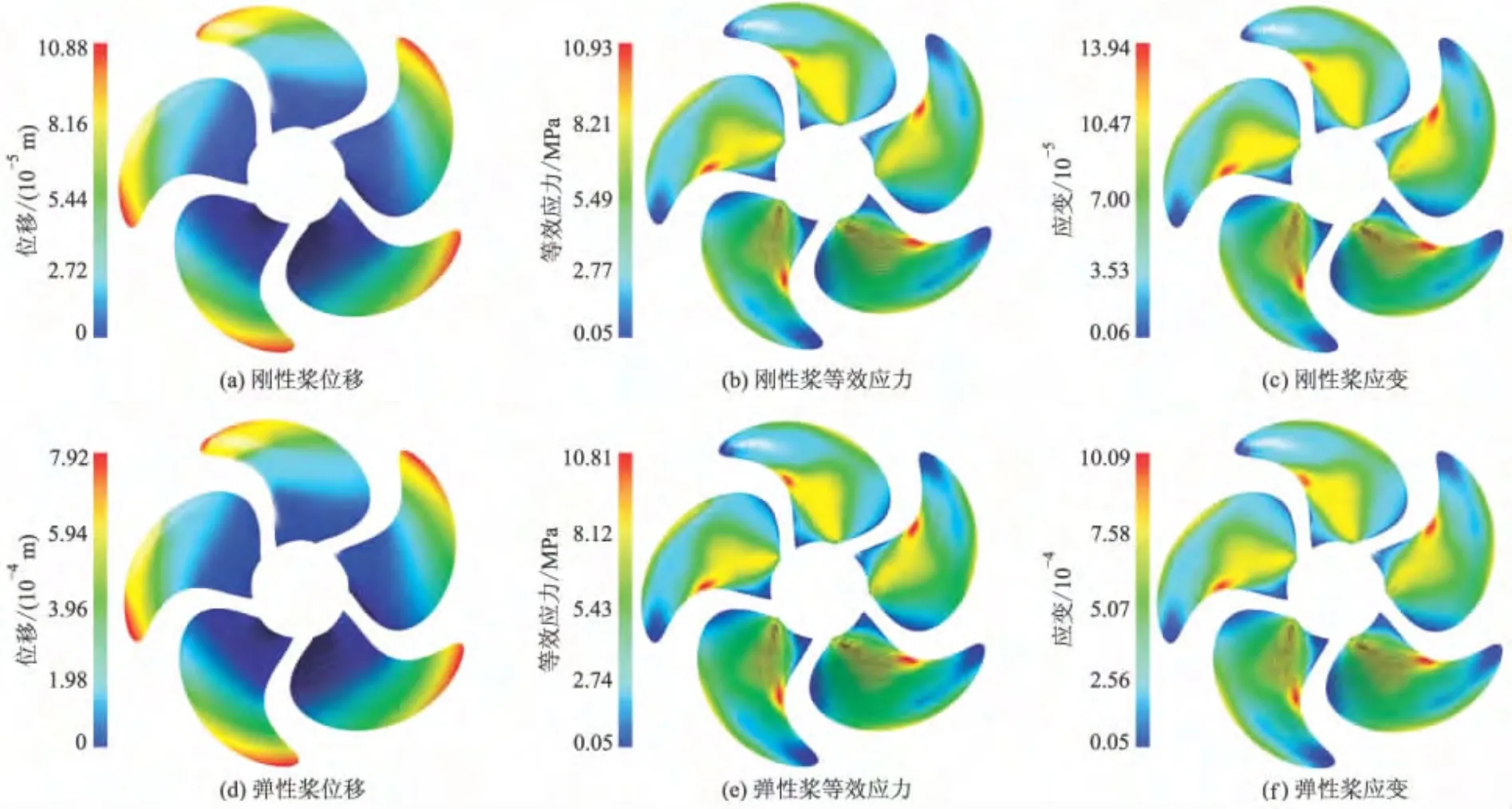
图8 刚性桨与弹性桨变形、应力及应变云图

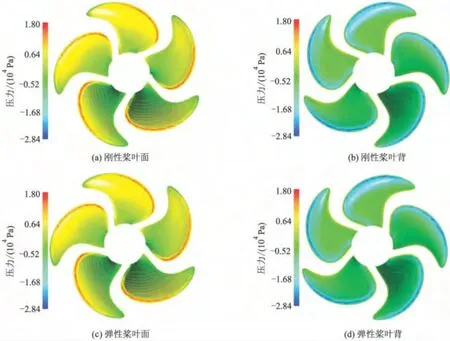
图9 刚性桨与弹性桨压力分布云图

图10 J=0.5时螺旋桨尾流特性的计算结果

图11 不同断面处的压力分布

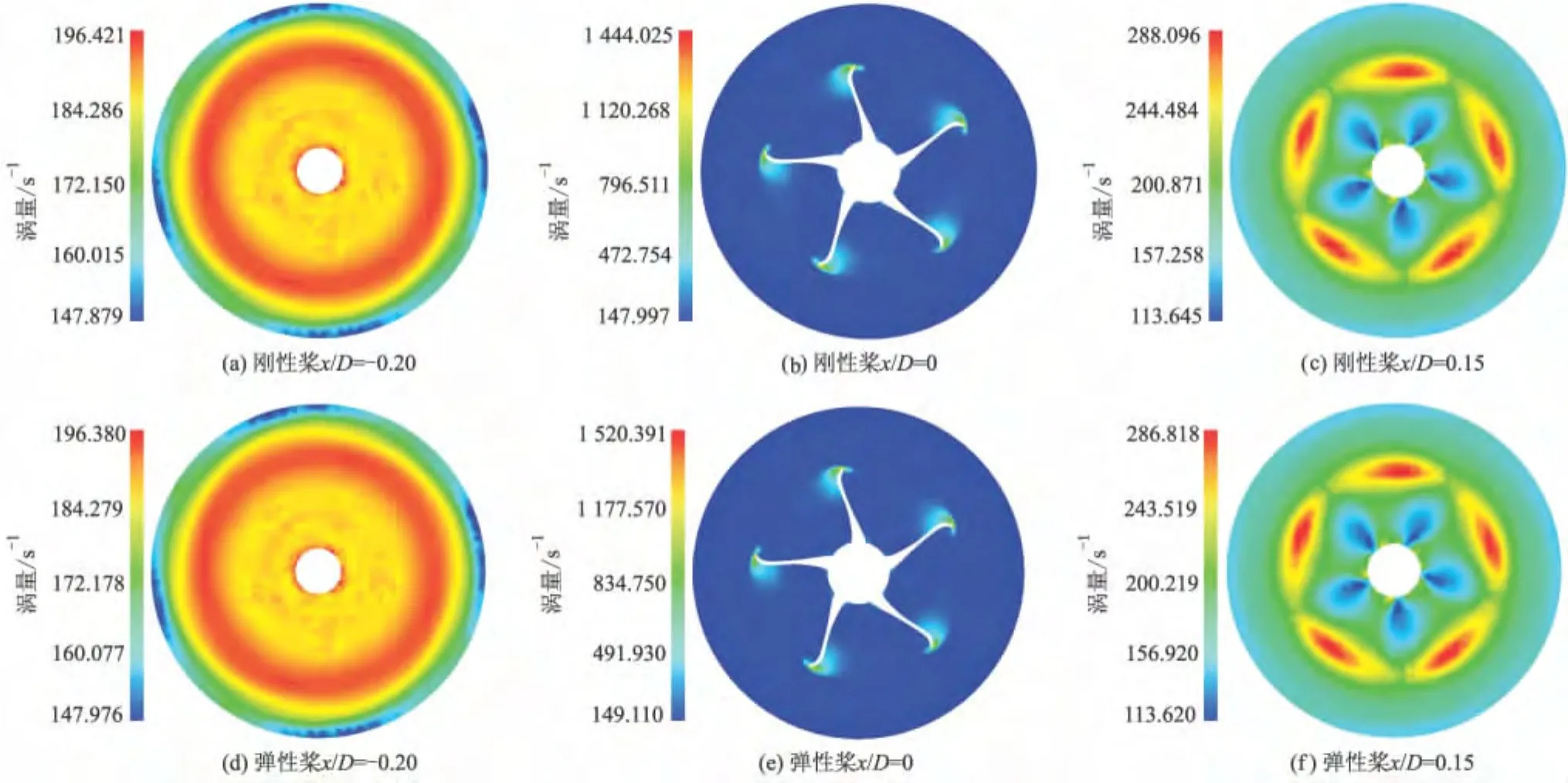
图12 不同断面处的涡量分布

4 结论

利用ANSYS软件中流体载荷与结构响应数据的双向传输技术，将流体与结构计算耦合在一起，给出了求解螺旋桨流固耦合问题的3维数值模拟方法.设定2种材料特性，对螺旋桨的水动力性能、桨叶变形及应力应变特性等进行了数值模拟.结果表明:弹性桨的变形与应变较刚性桨约高1个数量级.桨叶的变形又对水动力性能及周围流场产生了影响，弹性桨的推力和转矩均比刚性桨小.当转矩减小更多时，桨的效率有所提高.这一特性可用于复合材料螺旋桨的优化设计，可以实现螺旋桨整体性能的提升.

References)

［1］Lin G F.Comparative stress-deflection analyses of a thick-shell composite propeller blade［R］.Bethesda，MD:David Taylor Research Center DTRC/SHD-1373-01，1991.

［2］Lin H J，Lin J J.Nonlinear hydroelastic behavior of propellers using a finite-element method and lifting surface theory［J］.Journal of Marine Science and Technology，1996，1(2):114-124.

［3］Lin H J，Lai W M，Kuo Y M.Effects of stacking sequence on nonlinear hydroelastic behavior of composite propeller blade ［J］.Journal of Mechanics，2010，26(3):293-298.

［4］Lin C C，Lee Y J.Regression of the response surface of laminated composite structures［J］.Composite Structures，2003，62:91-105.

［5］Lin C C，Lee Y J.Stacking sequence optimization of laminated composite structures using genetic algorithm with local improvement ［J］.Composite Structures，2004，63:339-345.

［6］Lee Y J，Lin C C.Optimized design of composite propeller［J］.Mechanics of Advanced Materials and Structures，2004，11(1):17-30.

［7］Lin H J，Lin J J，Chuang T J.Strength evaluation of a composite propeller blade ［J］.Journal of Reinforced Plastics and Composites，2005，24(17):1791-1807.

［8］Blasques José PedroAlbergariaAmaral， Berggreen Christian，Andersen Poul.Hydro-elastic analysis and optimization of a composite marine propeller［J］.Marine Structures，2010，23:22-38.

［9］Sun Haitao，Xiong Ying.Fluid-structure interaction analysis of flexible marine propellers［J］.Applied Mechanics and Materials，2012，226:479-482.

［10］孙海涛，熊 鹰.桨叶变形对复合材料桨水动力性能影响［J］.华中科技大学学报:自然科学版，2013，41(6):81-85.

Sun Haitao，Xiong Ying.Effect of blade deformation of a composite propeller on its hydrodynamic performance［J］.Journal of Huazhong University of Science and Technology:Natural Science Edition，2013，41(6):81-85.(in Chinese)

［11］孙海涛，熊 鹰，黄 政.大侧斜螺旋桨水动力及变形特性研究［C］∥第十一届全国水动力学学术会议暨第二十四届全国水动力学研讨会.北京:中国海洋出版社，2012:961-967.

［12］孙海涛，熊 鹰.考虑变形的螺旋桨水动力及变形特性研究［J］.哈尔滨工程大学学报，2013，34(9):1108-1112.

Sun Haitao，Xiong Ying.Study on hydrodynamic and deformation performance of propellers considering the blade deformation［J］.Journal of Harbin Engineering U-niversity，2013，34(9):1108-1112.(in Chinese)

［13］Young Y L.Time-dependent hydroelastic analysis of cavitating propulsors［J］.Journal of Fluids and Structures，2007，23:269-295.

［14］Young Y L.Fluid-structure interaction analysis of flexible composite marine propellers［J］.Journal of Fluids and Structures，2008，24:799-818.

［15］Liu Z K，Young Y L.Utilization of bend-twist coupling for performance enhancement of composite marine propellers［J］.Journal of Fluids and Structures，2009，25:1102-1116.

［16］Motley M R，Liu Z K，Young Y L.Utilizing fluid-structure interactions to improve energy efficiency of composite marine propellers in spatially varying wake［J］.Composite Structures，2009，90:304-313.

［17］刘志华，熊 鹰，叶金铭.基于多块混合网格的RANS方法预报螺旋桨敞水性能的研究［J］.水动力学研究与进展，2007，22(4):450-456.

Liu Zhihua，Xiong Ying，Ye Jinming.Study on the prediction of propeller open-water performance using RANS formula and multi-block hybrid meshes［J］.Chinese Journal of Hydrodynamic，2007，22(4):450-456.(in Chinese)