车辆钢板弹簧悬架的有限元模型
柴 山,郭 明,徐上海,张 强,刚宪约
(1.山东理工大学交通与车辆工程学院,山东淄博 255049;2.济南交通高级技工学校,山东济南 250200;3.潍柴动力股份有限公司,山东潍坊 261001)
钢板弹簧是载货汽车上广泛应用的悬架弹性元件.它的优点是结构简单、工作可靠、成本低廉和维修方便,既是悬架的弹性元件,又是悬架的导向装置.它的一端与车架铰接,可以将路面作用于车轮上的垂直反力(支撑力)、纵向反力(牵引力和制动力)和侧向反力以及这些反力形成的力矩传递到车架(或承载式车身)上,同时它本身也有一定的摩擦减震作用.
在进行车架结构有限元分析时,钢板弹簧提供了车架的边界条件,钢板弹簧有限元模型能否较好地模拟真实钢板弹簧结构的工作情况,将直接影响到车架结构有限元分析的结果[1].因此对钢板弹簧悬架进行合理、正确的分析与简化,建立符合钢板弹簧悬架实际工作情况又简单实用且避免非线性分析的钢板弹簧悬架有限元模型是非常重要的.
笔者在研究钢板弹簧悬架的结构与工作特点的基础上,给出钢板弹簧有限元模型应该满足的4个基本条件,并总结和提出5种不同的钢板弹簧悬架简化模型.由某载货汽车的弯曲工况和制动工况的分析实例,对比分析5种模型的优缺点及对4个基本条件的满足情况,为钢板弹簧有限元模型建模提供参考.
1 钢板弹簧悬架的有限元模型
1.1 钢板弹簧悬架模型的基本要求
东风EQ1090E型汽车的钢板弹簧后悬架如图1所示,它由主钢板弹簧、副钢板弹簧、主簧前支架(卷耳支架)、吊耳、吊耳支架和副簧支架组成.与主簧直接安装在车架上不同,副簧与副簧支座之间有初始间隙δ0.在载荷较小时,副簧与副簧支座并不接触,副簧不受力,同时也就不对车架起支承作用,悬架刚度等于主簧刚度;当载荷逐渐增加,由于主簧变形,副簧支座随车架下移,直到消除了初始间隙δ0后,副簧与副簧支座开始接触,副簧与主簧共同支撑车架载荷,此时悬架刚度等于主簧刚度与副簧刚度之和.主副簧钢板弹簧悬架结构,根据所受载荷大小不同表现为分段线性刚度[2].

图1 东风EQ1090E型汽车的钢板弹簧后悬架
通过对钢板弹簧悬架的结构分析可以得出钢板弹簧悬架具有以下特点:①钢板弹簧相对于车轴对称,钢板弹簧与车轴的连接相当于铰接,为保持钢板弹簧平衡,前后支座铅垂反力相等;② 钢板弹簧的卷耳通过销轴与前支座连接,除可传递铅垂反力外还可传递水平推力和横向推力;③钢板弹簧通过吊耳与后支座连接,当钢板弹簧变形,弦长增大时,吊耳转动可以保证钢板弹簧弦长的自由伸缩,忽略吊耳引起的水平力,吊耳只传递铅垂反力和横向推力;④没有副簧的钢弹簧载荷与位移成线性关系,弹簧刚度是常数,有副簧的钢板弹簧载荷与位移成分段线的非线性关系,弹簧刚度是分段常数;⑤ 由于副簧与副簧支座之间有初始间隙δ0,只有在副簧支座下移,消除了初始间隙δ0后,副簧与副簧支座接触,副簧才开始发挥作用,因此副簧与副簧支座之间的变形之差为初始间隙δ0.
对于采用钢板弹簧悬架的汽车,钢板弹簧悬架提供了对车架和整车的全部位移约束.根据前述钢板弹簧悬架的5个特点,钢板弹簧悬架有限元模型应当满足以下基本要求:① 满足等支反力边界条件,作用于前后支座的竖直载荷相等;② 可传递水平载荷的能力,钢板弹簧有限元模型除可传递竖直载荷外,还可以传递纵向推力和横向推力;③ 满足简支梁边界条件,钢板弹簧有限元模型在卷耳处只能发生相对转动、不能发生纵向相对滑动,在吊耳处可以同时发生相对转动和纵向滑动;④满足主副簧边界条件,副簧发挥作用时,钢板弹簧有限元模型的弹簧刚度等于主簧刚度与副簧刚度之和,副簧末端与对应支座之间的相对竖直位移等于二者之间的初始间隙.
1.2 常用的几种钢板弹簧悬架有限元模型
车架坐标系的定义:汽车纵向对称面在车架第1横梁上平面的投影为x轴,向前为正;第1横梁中心轴为y轴,向右为正;根据右手法则,z轴竖直向上.
为进一步研究钢板弹簧的性质,建立更符合工程实际的钢板弹簧有限元模型,将对几种模型进行深入地分析和比较.首先用板壳单元建立1个完整的载货车边梁式车架有限元模型[3],如图2所示,在此基础上采用不同的钢板弹簧悬架模型,并进行只承受竖直载荷的弯曲工况和既承受竖直载荷又承受纵向载荷的制动工况的有限元分析,根据车架变形及支反力结果,检验各种钢板弹簧悬架有限元模型的合理性.

图2 施加竖直载荷的车架有限元模型
1.2.1 弯曲工况的载荷
车架的弯曲工况分析中各部件的重量以载荷的形式施加在车架上,主要施加的等效载荷:驾驶室4 620 N(包括2人)、发动机2 300 N、变速箱560 N、备胎机构378 N、货厢及货物43 720 N、油箱780 N、车架自重、电瓶320 N、减震器载荷2 800 N以及变速箱吊挂转矩为834 N·m,加载后的有限元模型如图2所示.
1.2.2 制动工况的载荷
制动工况考虑前后轮完全抱死的情况,取附着系数φ=0.7,汽车制动时的最大减速度为7.00 m·s-2[4].货车满载质量为 5 900 kg,制动时的惯性力大小为41 300 N,其中车架质量为270 kg,对车架施加纵向152.96 m·s-2的制动加速度就可以模拟出货车制动时惯性力.其他载荷施加及约束条件与弯曲工况相同.钢板弹簧的参数如表1所示.

表1 钢板弹簧的参数
应用SANS电子万能试验机进行钢板弹簧的刚度测试得到载荷位移曲线如图3所示,曲线为一条直线,钢板弹簧刚度是常数.
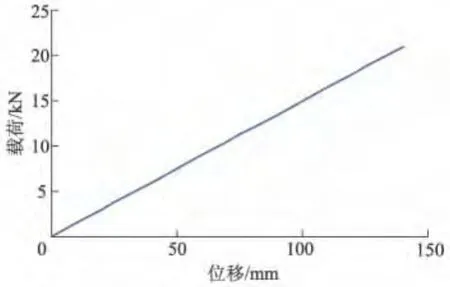
图3 钢板弹簧的载荷位移曲线
1.2.3 5种方案的受力情况分析
下面对5种常用的板簧支座有限元模型在弯曲和制动2种工况下车架的受力情况进行讨论.5种方案的车架模型均用上文已建立的车架模型,并依据钢板弹簧刚度试验得到的结果将悬架的前簧和后簧刚度全部设定为171 000 N·m-1.
1)方案1为独立螺旋弹簧(轴向压缩弹簧)单元模型.把钢板弹簧悬架简化为在板簧悬架支座处的弹性支座,为了避免应力集中,每个弹性支座用1组(9个)并联的螺旋弹簧单元代替.为了保证钢板弹簧刚度一致,由试验数据及文献[5]中的公式得出每根螺旋弹簧的刚度为9 500 N·m-1.将车架的几何模型进行网格剖分,在悬架支座处找相邻多个节点,把节点竖直向下复制,本方案中节点在竖直向下复制0.3 m,分别用弹簧单元(在 ANSYS中是COMBIN14单元)连接上下对应节点,并将弹簧的属性设为轴向伸缩弹簧,每根弹簧设为相同的刚度:

式中:K为该板簧支座处的弹簧刚度;n为该支座处弹簧单元的个数.
以弯曲工况和制动工况为例,讨论等效钢板弹簧悬架的边界建模方法的合理性和适用性.对于弯曲工况,在每根弹簧单元下端的节点处施加位移约束,限制各节点的3个方向的平动自由度.因为螺旋弹簧单元只能承受轴向载荷,即竖直载荷,不能承受侧向力,所以需要在车架上任选一个节点约束车架的水平平动和转动,不妨将此节点选在某一横梁的中间位置[5].施加位移约束后的车架有限元模型如图4所示.
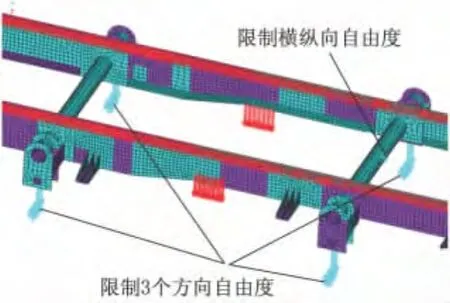
图4 弹簧单元与车架的位移约束
计算结果如表2所示,弯曲工况下此方案得到的钢板弹簧悬架各处支反力与实际情况严重不符.以左前钢板弹簧为例,吊耳处的竖直反力竟然比卷耳处高出1倍;制动工况下,由于弹簧单元不能承受横向应力,导致车架位移较大,可见此方案弹簧不能承受纵向推力,与钢板弹簧特性不符.

表2 钢板弹簧两端受力N
2)方案2为刚性梁-螺旋弹簧(轴向伸缩弹簧)组合模型.分别用1根竖直螺旋弹簧与钢板弹簧的卷耳、吊耳支座的多个节点以RBE3方式连接,同时将同一钢板弹簧的前后2组竖直弹簧的下端用1根刚性梁连接起来[6].在每根刚性梁的中部1个节点上施加3个方向的平动自由度约束,同时还必须像方案1一样在车架的合适节点上施加水平平动和转动自由度约束.采用该方案建立的车架有限元模型如图5所示.

图5 刚性梁-螺旋弹簧组合悬架模型
计算结果如表2所示,钢板弹簧前后卷耳、吊耳处的支反力相等,满足1.1节中的等支反力条件.同样,该方案也只能承受竖直载荷,由于制动时纵向载荷的作用,在车架上用于约束车架水平位移的节点位置产生较大的应力值,如图6所示.比较方案1,2可知:车架整体受力和变形更接近实际情况,但车架上用于约束水平自由度的节点处出现不正确的高应力区,是这2种采用螺旋弹簧作为弹性支承的钢板弹簧悬架有限元模型共同的缺点.

图6 车架位移约束点处的高应力区
3)方案3为等效弧形薄板模型.采用与实际钢板弹簧等弧高、等弧长、等宽度和等刚度的一条纵向弧形薄板来模拟实际的钢板弹簧悬架,薄板采用板壳单元进行剖分.在卷耳处弧形薄板的上边缘节点与卷耳销轴的对应节点耦合3个方向的平动自由度,多组对应节点的自由度耦合将使得弧形薄板只能与卷耳发生相对转动;在吊耳处,弧形薄板的上边缘节点与吊耳上的对应节点相互耦合竖直方向和左右横向平动自由度,多组对应节点的自由度耦合将使得弧形薄板只能与吊耳发生纵向相对滑移和相对转动[7].整车模型的位移边界全部施加在弧形薄板(即钢板弹簧)的中间对称线上的1组节点,一般可以在后桥钢板板簧位置处施加3个方向的平动自由度约束,在前桥钢板弹簧位置处施加横向和竖直2个方向的平动自由度约束,放松纵向自由度,以使车架弯曲时可以产生纵向位移,不会对车架产生过约束.
除了几何参数外,等效弧形薄板模型的1个重要参数就是薄板的厚度.为了确保弧形薄板的竖直刚度和实际钢板弹簧相等,可以这样确定薄板的厚度[8]:单独建立1个具有相同几何参数的弧形薄板模型,以简支梁的形式在弧形薄板两端施加位移约束,在弧形薄板的中间最大弧高处的1组节点上均匀施加竖直方向载荷,使其合力等于给定的钢板弹簧悬架竖直刚度值;给定弧形薄板大概的厚度区间,采用二分法进行迭代,当施加载荷点的竖直位移大于1时应增大当前板厚,小于1时减小板厚,直到位移δ满足|δ-1|≤ε时为止,取此时的厚度为钢板弹簧等效弧形薄板有限元模型的板单元厚度.另一种方法是采用材料力学中的悬臂梁变形公式来估算弧形薄板的厚度:

式中:t,b,l分别为弧形薄板厚度、宽度和弧长;K,E分别为钢板弹簧刚度和弹性模量.
取前簧的厚度为19.500 mm,后簧的厚度为15.754 mm.考虑到板簧可能发生大变形,为考察采用线弹性分析是否会与大变形分析有较大的误差,分别对同一板簧的有限元模型进行了线性弹性分析和大变形非线性分析[9].结果表明:在载荷为17 425 N时,大变形分析所得的竖直最大变形为106.285 mm,小变形结果为102.389 mm,两者之间的误差为3.81%,因此用小变形分析代替大变形分析可满足工程要求.
采用钢板弹簧悬架的等效弧形薄板模型计算分析车架的弯曲工况,前后悬架的自由度耦合和位移约束分别如图7,8所示.钢板弹簧两端受力情况的计算结果如表2所示,由表2中钢板弹簧支反力的数据可以看出:卷耳和吊耳处的支反力相等,能够满足1.1中提出的条件①,②和③.由于弧形薄板简化悬架模型具有纵向和横向承载能力,因此无需在车架上再施加额外约束,在制动工况也不会引起局部的不恰当应力集中.
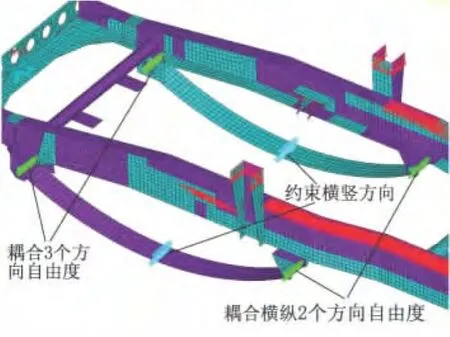
图7 前簧的约束及耦合情况
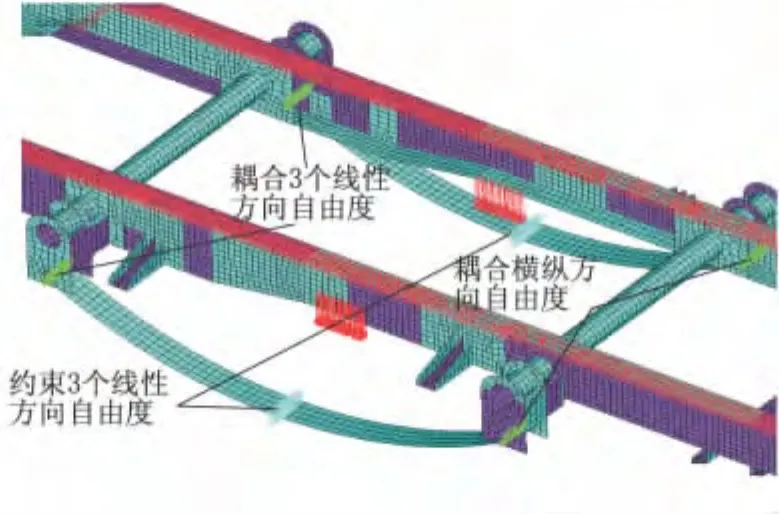
图8 方案3后簧的约束及耦合情况
4)方案4为等效弧形薄板模型+吊杆.此方案是用板壳单元SHELL181和杆单元LINK8共同模拟板簧,板壳单元模拟实际中的钢板弹簧,杆单元模拟实际中的吊耳结构,这样可以使模型更加贴近实际情况.在卷耳处弧形薄板的上边缘节点与卷耳销轴的对应节点耦合3个方向的平动自由度,多组对应节点的自由度耦合将使弧形薄板只能与卷耳发生相对转动,模拟吊耳的1组杆单元因为其节点只有3个方向的平动自由度,将其直接与车架、钢板弹簧末端对应的节点相连即可.此方案仍采用方案3模拟的钢板弹簧厚度.整车模型的位移边界施加方法同方案3,如图9所示.

图9 方案4后簧的约束及耦合情况
计算结果如表2所示,各钢板弹簧变形时,弦长增大,吊耳处均发生纵向的水平位移,可承受纵向推力,符合钢板弹簧特性.方案3,4都能准确地模拟钢板弹簧的工作特性,方案4比方案3的模型复杂,但它可以比较准确地计算吊耳支座处的反力.
5)方案5为等效弧形薄板模型+副簧约束方程.具有副簧的钢板弹簧悬架在副簧末端与其支座之间存在一初始间隙δ0,轻载时只有主簧起作用,在重载时主簧将和副簧共同起作用,在分析车辆承受满载的工况时,副簧已经处于承载状态,钢板弹簧悬架的刚度是主、副簧刚度之和.如果建立有限元模型时,直接在模型中将主簧与其支座相连、副簧与其支座相连,虽然二者的合成刚度与实际悬架相等,但由于主副簧的变形不一样,承受的载荷与实际状态有很大差异:主簧载荷将大大小于实际载荷,副簧载荷大大高于实际载荷[10].因此,建立带有副簧的钢板弹簧悬架模型时,必须保留副簧与其支座之间的初始间隙,并建立副簧与其支座位移之间的约束方程如下:

式中sLz和sBz分别为副簧及其支座上耦合点的垂向位移.
此方案中所用约束方程的const为空载时副簧与车架的间隙,即保证副簧上耦合的点在垂直方向上的位移比车架上耦合点的位移低50 mm.副簧刚度采用138 000 N·m-1,其厚度模拟与方案3厚度模拟方法一致.采用弧形薄板简化钢板弹簧、主簧端部自由度耦合、副簧端部约束方程定义的轻型货车后悬架模型如图10所示.
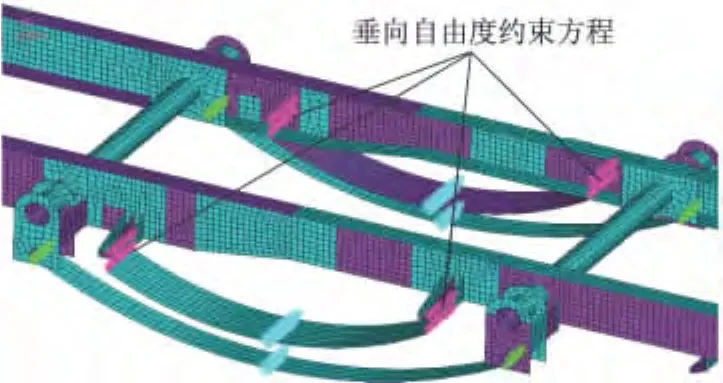
图10 轻型货车的主副簧钢板弹簧悬架模型
进入通用后处理模块获得钢板弹簧两端受力情况如表2所示,该方案车架的整体位移较均匀,未出现前面翘起的情况,说明对后簧的弹簧刚度模拟较合适,副簧在满载情况下发生作用;前后簧变形时,弦长增大,吊耳处均发生纵向的水平位移,可以承受纵向推力作用,则此方案可准确模拟主副簧共同作用时的钢板弹簧特性.
2 钢板弹簧悬架的有限元模型分析
前面讨论了各种钢板弹簧有限元模型的简化方案,并在相同条件下(即相同的车架有限元模型、相同的载荷和相同的钢板弹簧刚度)进行了各种方案弯曲工况和制动工况的静力分析,求得钢板弹簧两端受力情况如表2所示,对5种方案的特点进行总结如下:
1)方案1的钢板弹簧有限元模型只能承受垂直方向的载荷,且每个弹簧的吊耳和卷耳两处的垂直方向受力不相等,这与钢板弹簧特性不符,相对于实际情况的误差较大.此方案结构简单,建模方便,适用于选用悬架时,对悬架刚度进行大致的估算.
2)方案2钢板弹簧模拟板簧的承载能力从结构上看较方案1有所改善,较为逼近板簧的结构,每个弹簧的吊耳和卷耳两端垂直方向受力相等.但是此方案的弹簧单元不能承受横向载荷,因此吊耳和卷耳处不能承受横向推力作用,这与钢板弹簧特性不符.
3)方案3钢板弹簧的模拟几何形状接近真实的板簧,并且满足钢板弹簧悬架有限元模型的等支反力边界条件、可传递水平推力和横向推力以及在卷耳处只能发生相对转动、不能发生纵向相对滑动,在吊耳处可以同时发生相对转动和纵向滑动的3项要求.
4)方案4是对方案3的一种改进,即在方案3的基础上考虑吊耳的结构,建立吊耳的有限元模型,此方案的悬架构造更贴合实际的悬架构造.方案4的结构比方案3复杂,其分析结果与方案3相近,同时验证了方案3对车架应力计算也比较可靠.
5)方案5是在方案3的基础上加以改进,在此基础上增加了副簧,前簧和主簧的约束与耦合情况与方案3一致,而副簧与车架的约束采用约束方程,从板簧实际结构组成上,增加副簧是对真实情况的模拟.该方案考虑了副簧的作用,有效模拟了分段线性的非线性关系的载荷位移关系,与实际情况吻合度较高.
综合比较以上5种钢板弹簧有限元模型,对于1.1节中提出的钢板弹簧有限元模型的4项基本要求的满足情况如表3所示.

表3 5种模型对4项基本要求的满足情况
3 结论
通过对钢板弹簧悬架的结构与工作特点的分析给出了钢板弹簧有限元模型应该满足的4个基本条件.通过某实例的弯曲工况和制动工况的分析,研究了5种不同的钢板弹簧悬架简化模型.对于一般的钢板弹簧悬架,利用方案3中的模型即可达到很好的建模效果,而对于含有副簧的悬架,则可采用建立副簧与其支座位移之间的约束关系来建模即可达到很好的效果,也能满足各项基本要求,建议在钢板弹簧悬架有限元模型构造时以方案3,5为基础进行,这样能较容易得到合适的有限元模型.
References)
[1]陆 波.板簧模型对车架强度计算的影响分析[J].汽车技术,2002(4):9-10.
Lu Bo.Analysis of effect of leaf spring modes on calculation of strength of frames[J].Automotive Technology,2002(4):9-10.(in Chinese)
[2]Liu Hanyi,Su Ganlong.A double thick beam FEM of dynamics analysis based on spline wavelets in automobile leaf spring[C]∥The Sixth Asian Conference on Multibody Dynamics.2012:49-54.
[3]Chai Shan,Wang Yougang,Wang Pengcheng,et al.A research and application of parametric modeling technology for truck frame base on ANSYS[J].Key Engineering Materials,2011,460/461:534-539.
[4]Gang Xianyue,Chai Shan,Ren Chuanbo,et al.Research on the load state nonlinearity problem of truck frame under braking conditions[J].International Journal of Advancements in Computing Technology,2010,23(4):58-66.
[5]刚宪约,张 帆,柴 山,等.空气弹簧悬架客车的转弯、扭转工况有限元建模方法研究[J].汽车工程,2013,35(12):1099-1104.
Gang Xianyue,Zhang Fan,Chai Shan,et al.FE modeling method for an air suspension bus under turning and torsion conditions[J].Automotive Engineering,2013,35(12):1099-1104.(in Chinese)
[6]李丽君,刚宪约,李红艳,等.车架有限元分析中的自由度耦合技术[J].农业装备与车辆工程,2008(10):3-5.
Li Lijun,Gang Xianyue,Li Hongyan,et al.DOF coupling techniques in the finite element analysis of vehicle frame[J].Agricultural Equipment&Vehicle Engineering,2008(10):3-5.(in Chinese)
[7]MSC Software Gorp.MSC/NASTRAN2004r1Reference Manual[M].Santa Ana,USA:MSC Software Gorp,2004.
[8]柴 山,李基恒,刘书田,等.串联多轴油气弹簧悬架车辆车架强度分析[J].机械科学与技术,2004,23(4):408-411.
Chai Shan,Li Jiheng,Liu Shutian,et al.Strength analysis for the vehicle frame with series-arranged multiaxes oil and air spring suspensions[J].Mechanical Science and Technology,2004,23(4):408-411.(in Chinese)
[9]Kueh Joo-teck Jeffrey,Faris Tarlochan.Finite element analysis on the static and fatigue characteristics of composite multi-leaf spring[J].Journal of Zhejiang University Science A:Applied Physics&Engineering,2012,13(3):159-164.
[10]雷昌浩.汽车钢板弹簧计算的一种新模型及其静动态特性研究[D].柳州:广西工学院汽车与交通学院,2010.

