基于能量法的注浆抬动变形

陈 娟，徐力生，徐 蒙，张 帆

(1.中南大学地球科学与信息物理学院，湖南长沙410083;2.中南大学机电工程学院，湖南长沙410083)

注浆抬动效应是岩土注浆领域研究的热点，国内外相关专家围绕岩土注浆过程中的地层抬动效应展开了大量研究，王广国等［1］研究了压密注浆过程中的地层抬动机理，并推导了压密注浆过程中地层抬动位移的解析解.唐智伟等［2］从控制地表沉降的角度出发，基于镜像原理［3-4］推导了注浆引起地层抬动的位移解，提出了一种注浆抬动地层的数值模拟方法.侯艳娟等［5］在分析建筑物沉降恢复特点的基础上，研究注浆抬动机制，提出地层充填密实、止浆围护形成、抬动力形成及建筑物结构抬动的4个阶段作用模式.李立新等［6］基于随机介质理论，假设多孔注浆抬动量为单孔注浆抬动量的线性叠加，分别建立了单孔与多孔注浆抬动量的随机介质预测模型，但多孔时计算结果与实际偏差较大.边学成等［7］针对铁路路基的沉降问题，采用非水反应高分子聚合物填充注浆的方法使轨道均匀抬动，并采用大型物理试验验证了所用方法的有效性.

混凝土盖重堆石坝在水利水电工程中是一种常见的坝型，而此坝型的固结注浆和帷幕注浆一般都是在混凝土盖重上进行施工.在施工中经常会引起混凝土盖重的抬动变形，甚至可能使混凝土盖重产生裂缝，从而严重影响盖重的整体性和防渗能力.目前控制抬动变形的方法主要依靠现场仪器监测以及工程经验，而对于混凝土盖重注浆抬动变形的机理研究还较为缺乏.为此，本研究针对混凝土盖重注浆过程中出现的抬动变形这一工程问题，通过对土体与混凝土盖重进行受力分析，建立混凝土盖重注浆抬动变形的势能方程，并基于最小势能原理推求盖重注浆抬动变形值的解析解，分析各注浆参数对该抬动变形值的影响.然后引入工程实例，采用有限元分析软件ABAQUS对实例进行仿真模拟，并与理论分析结果对比，以期在一定程度上提升混凝土盖重注浆技术的科学性，从而为注浆工程的规范化、精细化施工提供指导.

1 混凝土盖重受力分析

1.1 注浆引起的混凝土盖重抬动变形

混凝土盖重固结注浆抬动的主要原理是由于注浆引起土体体积膨胀，从而克服浆液上方倒圆台土体重力、土体剪切力以及混凝土盖重重力使混凝土盖重抬动变形.由于盖板有钢筋网分布，可以把它看成一个线弹性体.盖重主要受自身重力以及通过土体传递的注浆压力作用.随着注浆压力的增大，浆液上方的土层与岩层将会形成一个倒锥形剪切面.注浆压力产生的上抬力p使土体抬动的条件是p需要克服混凝土盖重的自身重力Gm、倒锥形土体自身重力Gt以及倒锥形侧表面的剪力Ft，此时，混凝土盖重将发生上抬现象.当产生抬动变形时，混凝土盖重与土体受力分析如图1所示.注浆时，混凝土盖重有向上抬的趋势，如图2所示.

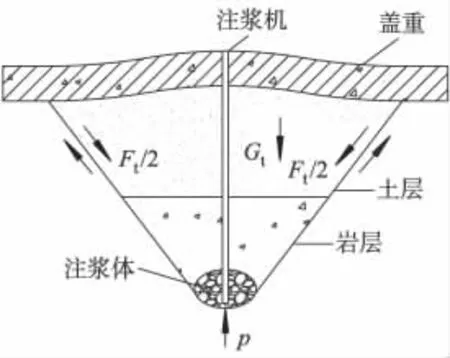
图1 混凝土盖重抬动变形受力分析

图2 混凝土盖重抬动变形示意图

设混凝土盖重变形的弯曲方程［8-9］为

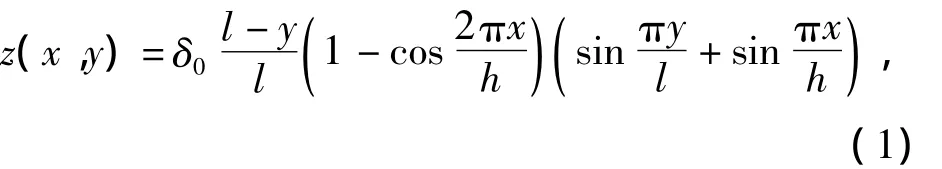
式中:δ0为与混凝土盖重变形位移有关的系数;l为混凝土盖重长度;h为混凝土盖重宽度.

1.2 土体上的注浆压力

由于在注浆时混凝土盖重抬动变形允许的位移比较小，因此，假设注浆压力在土体中均匀分布，土体上抬受到均布的注浆压力［10］为

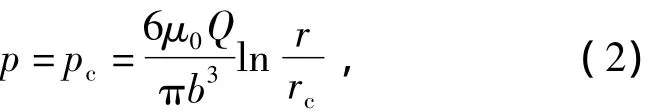
式中:pc为注浆孔内注浆压力;μ0为浆液运动黏度;b为裂缝宽度;r为浆液扩散半径;rc为注浆孔半径;Q为注浆量.

2 能量分析

注浆时，总的势能包括注浆压力引起的外力势能、混凝土盖重弯曲应变能、混凝土盖重重力势能、倒圆台土体的重力势能以及克服浆液上方倒圆台土体侧表面剪切力所消耗的一部分能量.

2.1 外力势能

如果采取均布荷载，则压力的衰减只与浆液的扩散半径有关，注浆区域扩散半径r内受均布荷载p作用的外力势能为

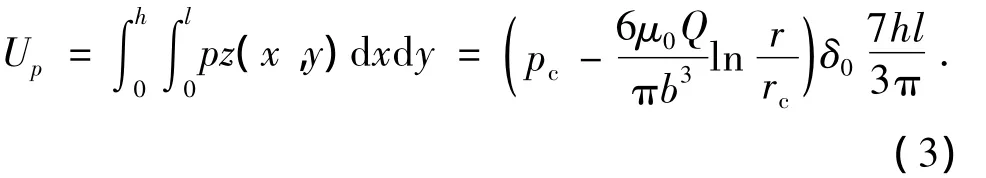
2.2 混凝土盖重的应变能与重力势能

混凝土盖重受力弯曲变形产生的应变能为

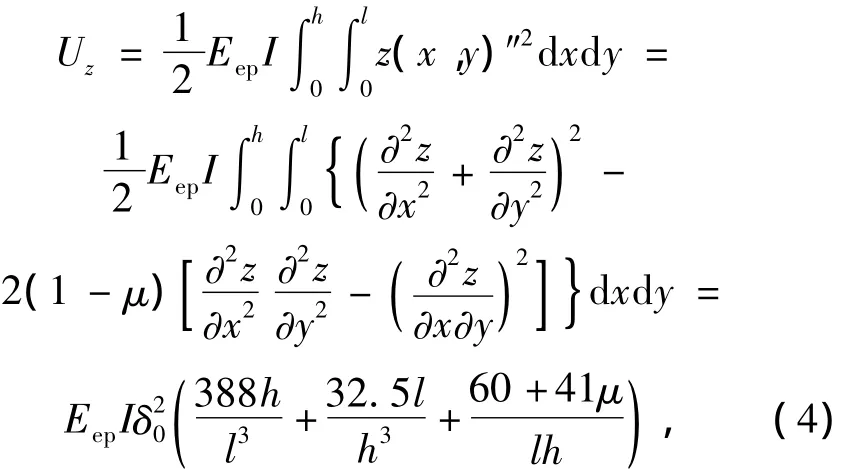
式中:μ为混凝土盖重的泊松比;Eep为混凝土盖重弹性模量;I为惯性矩，I=lh31/12;h1为混凝土盖重厚度.

混凝土盖重的重力势能为

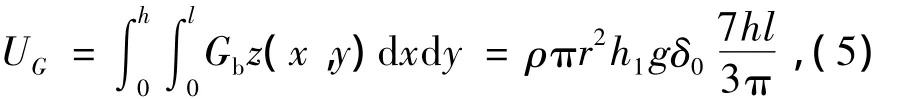
式中ρ为混凝土盖重重度.

2.3 土体的重力势能与剪切能

浆液通过渗透、填充、挤密和劈裂等4种方式在地层中作用［11］，浆液上方倒圆台土体重力Gt与浆液上方倒圆台土体侧表面剪切力Ft分别为［12］

式中:a为倒圆台土体高度，a=0.5(B-2r)×tan(θ +φ);B为混凝土盖重抬动区域的最大跨度;r 2为注浆体半径;θ为破坏面与水平方向夹角;φ为土体内摩擦角;γ为土体的重度.则克服Gt和Ft做功消耗的能量为

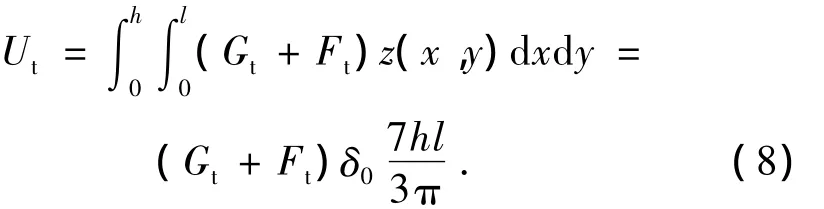
2.4 注浆系统总势能

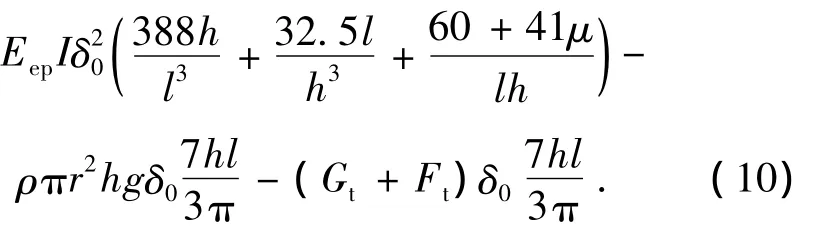
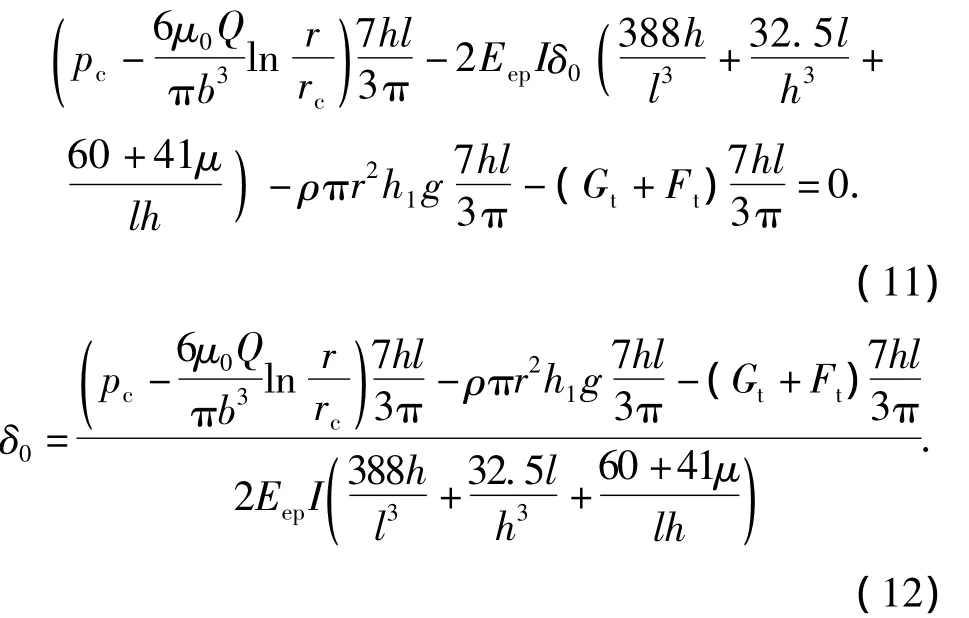
将式(12)代入式(1)，得混凝土盖重固结注浆混凝土盖重抬动变形的解析解为

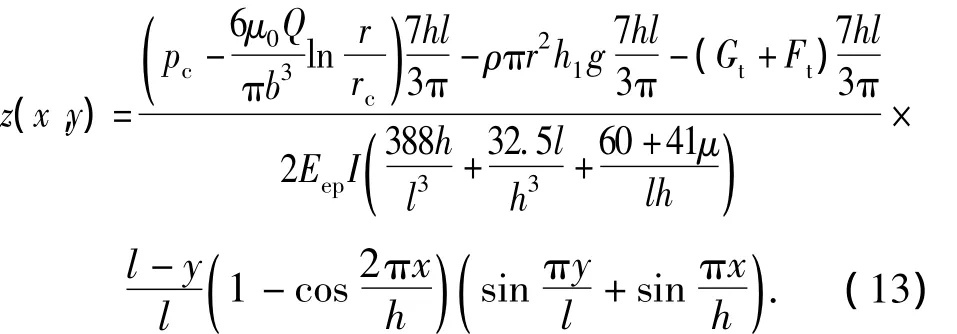
3 多孔注浆对混凝土盖重抬动的影响

3.1 注浆孔分布形式

在沿圆周等间距布孔方案下，分析多孔同时注浆对混凝土盖重抬动的影响如图3所示.设有n个注浆孔沿着圆周等间距布置，各孔注浆压力pc相等，注浆的布孔半径为R.

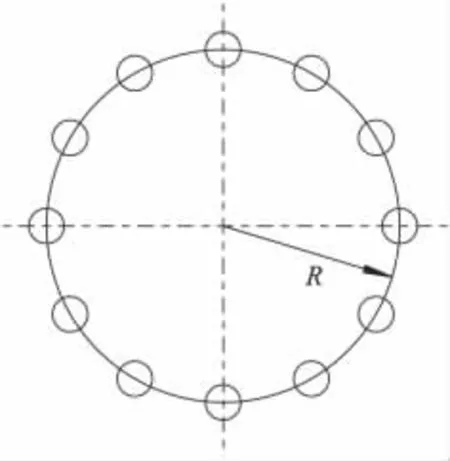
图3 注浆孔分布形式

根据式(2)，注浆流场中任意一点M的注浆压力［13］为

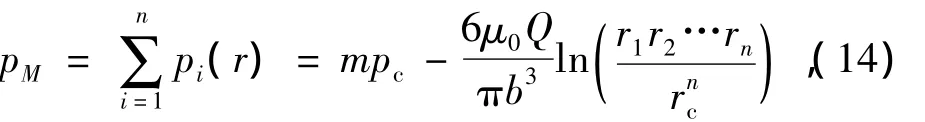
式中r1，r2，…，rn为各注浆孔中心与M的距离.

3.2 多孔注浆能量分析

工程实际中，混凝土盖重固结注浆通常采用多个注浆孔同时施工，其影响往往叠加.多孔注浆引起的混凝土盖重变形比单孔注浆更加复杂，由于浆液的膨胀将对混凝土盖重下方土体产生扰动，对其作用范围内的其余注浆孔产生影响，从而导致较大的地表抬动位移.当注浆孔间的间距较大时，相互影响较小，可用叠加法计算最终混凝土盖重抬动位移.本研究将多孔注浆引起的混凝土盖重抬动位移视为单孔注浆引起的抬动位移的线性叠加.则多孔注浆时的外力势能为

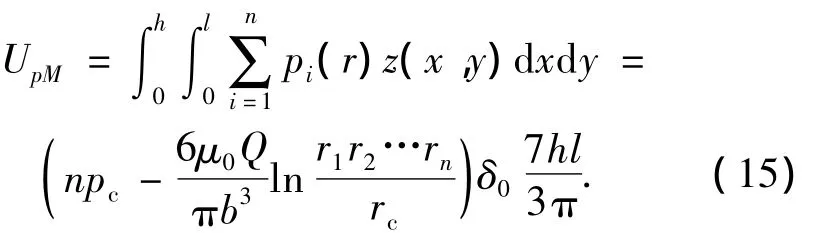
多孔注浆时混凝土盖重的应变能与重力势能分别为

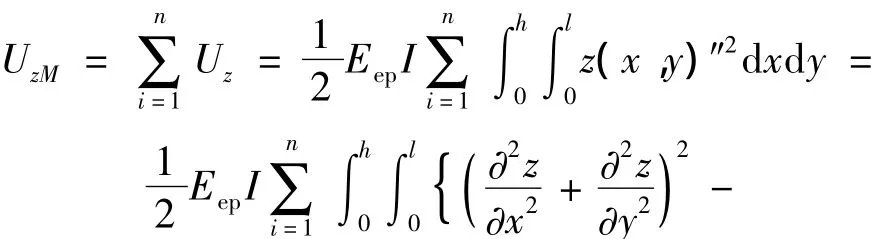
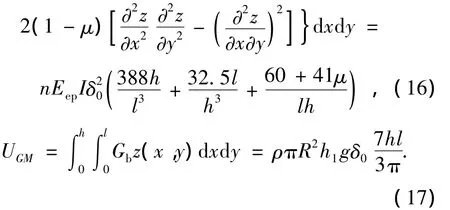
多孔注浆时，土体的重力势能与剪切能如式(18)所示，系统总势能如式(19)，(20)所示.

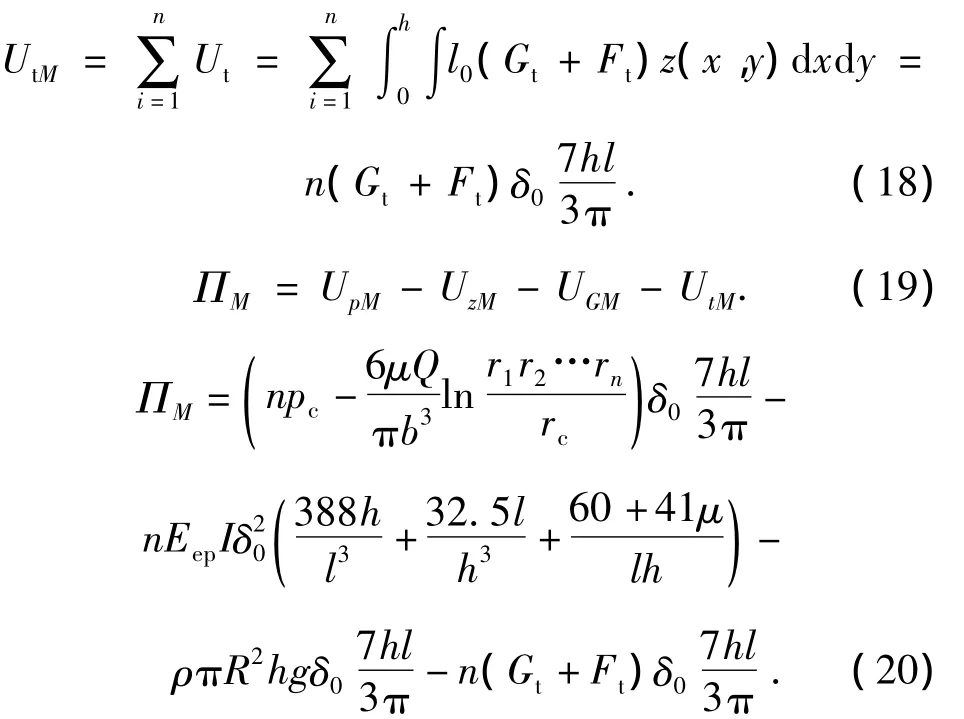
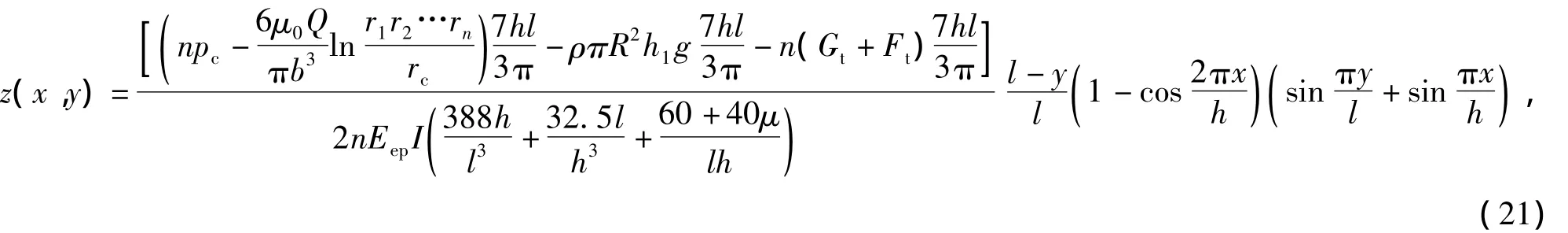
4 工程实例分析

以某大坝混凝土盖重固结注浆施工为例，土体、面层、注浆参数根据施工现场岩土条件以及相关试验资料确定.盖重主要力学特性参数:弹性模量Eep=26 480 MPa，泊松比 μ =0.167，重度 ρ=24.0 kN·m-3;土体主要力学特性参数:弹性模量Eep=2 540 MPa，泊松比 μ =0.200，重度 ρ=21.5 kN·m-3，黏聚力 c=25 kPa，内摩擦角 φ =40°，膨胀角θ=20°.混凝土盖重注浆试验参数:注浆压力pc=4 MPa，注浆半径r=1.2 m，注浆深度a=5m，注浆管半径rc=0.025 m，裂缝宽度b=0.03 m，浆液流量Q=33 L·min-1，浆液黏度 μ0=0.001，混凝土盖重尺寸l×h×h1=60m×10m×0.8m.有限元法是分析混凝土这类非线性材料变形的一个有效方法［14］，本研究结合有限元软件ABAQUS与推导的理论模型，分别分析单孔和多孔注浆条件下的混凝土盖重抬动位移.

4.1 单孔注浆参数分析

4.1.1 注浆压力对混凝土盖重抬动位移的影响

在保持原方案其他设计参数不变条件下，将注浆压力分别设计为1.45，2.40，3.25和4.00 MPa时，盖重相应的抬动位移变化曲线如图4所示.

图4 注浆压力一定时，最大抬动位移随注浆深度变化关系

由图4可知:不同的注浆压力对盖重抬动位移值的影响较大，混凝土盖重抬动位移值随注浆压力的增加而增大，这是因为注浆压力增加时，通过土体作用于盖重上的压力增加，从而使混凝土盖重的变形位移增大.盖重抬动位移值对注浆压力变化比较敏感，因此注浆时要合理设计此参数，以保证混凝土盖重抬动位移值在工程许可范围内.

4.1.2 注浆半径对混凝土盖重抬动位移的影响

在保持原方案其他设计参数不变的条件下，考虑注浆半径分别为0.6，1.2，1.8和2.4 m时，混凝土盖重相应的抬动位移变化曲线如图5所示.由图5可知，混凝土盖重抬动位移值随注浆半径的增加而减小.这是因为注浆半径增加时，浆液上方形成的倒圆台体积增加，使土体的重力势能与土体剪切破坏所需要的能量增大，从而使得通过土体作用于混凝土盖重上的压力减小，造成抬动位移值减小.

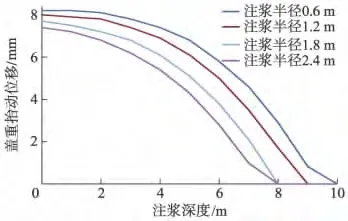
图5 注浆半径一定时最大抬动位移随注浆深度变化关系

4.1.3 混凝土盖重厚度对抬动位移的影响

在保持原方案其他设计参数不变的条件下，将混凝土盖重厚度分别设计为0.5，0.8和1.2 m时，相应的抬动位移变化曲线如图6所示.由图6可知，混凝土盖重抬动位移随厚度增加而略有减小，但变化不大.这说明与注浆压力、注浆半径相比，混凝土盖重厚度对于抬动位移的影响相对较小.

图6 混凝土盖重厚度一定时，最大抬动位移随注浆深度变化关系

4.2 多孔注浆参数分析

为了验证所推导的多孔注浆的混凝土盖重抬动位移计算模型的有效性，依据前述的土体和混凝土盖重参数，采用ABAQUS建立盖重抬动变形分析模型.分析在不同注浆孔间距和注浆孔数目下混凝土盖重的抬动位移.

4.2.1 注浆孔间距对混凝土盖重抬动位移的影响

在保持原方案其他设计参数不变的条件下，采用6个注浆孔同时注浆，注浆孔沿圆周均匀分布，分别分析在不同注浆孔间距下混凝土盖重相应的抬动位移，得到抬动位移的理论解、数值解与实测值如图7所示.由图7可知，抬动位移值随着注浆孔间距增加而显著减小.说明注浆孔间距对于混凝土盖重抬动位移的影响较大，这是因为随着注浆孔间距增大，作用于混凝土盖重上的压力由集中变得分散，导致单位面积混凝土盖重受力减小，从而使得混凝土盖重抬动位移减小.

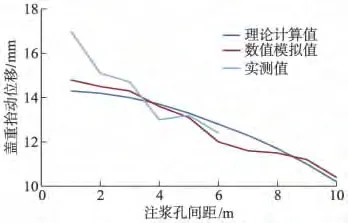
图7 注浆孔间距与混凝土盖重最大抬动位移的关系

4.2.2 注浆孔数目对抬动位移的影响

在保持原方案其他设计参数不变的条件下，根据文献［12］结果，将注浆孔间距固定在4 m，得到混凝土盖重抬动位移的理论解、数值解与实测值如图8所示.由图8可知，混凝土盖重抬动位移随注浆孔数目增加而逐渐增加，但当注浆孔数目大于5个时，抬动位移增加不再明显.这是因为当注浆孔间距固定时，随着注浆孔数目增加，注浆孔间的相互扰动越来越强烈，导致注浆压力衰减较大，当注浆孔数目大于一定值后，其对抬动位移的影响减小.

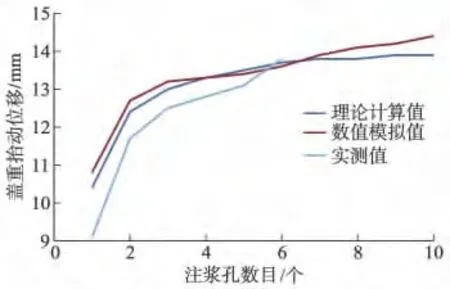
图8 注浆孔数目与混凝土盖重最大抬动位移的关系

5 结论

1)根据大坝混凝土盖重固结注浆时混凝土盖重的受力特性，建立势能方程.根据最小势能原理分别推导了单孔与多孔均布注浆条件下混凝土盖重抬动位移解析解的表达式.

2)基于所推导的解析表达式，分析了注浆压力、注浆半径以及混凝土盖重厚度对抬动位移的影响.结果表明:注浆压力与注浆半径对于抬动位移均有较大影响，混凝土盖重厚度对抬动位移影响较小.因此，在混凝土盖重固结注浆工程中，应经济合理地设计注浆参数，以保证混凝土盖重抬动位移在工程许可范围内.

3)结合工程实例与ABAQUS有限元分析，对所推导的解析表达式进行了验证，结果表明了解析解的有效性.

References)

［1］ 王广国，杜明芳，苗兴城.压密注浆机理研究及效果检验［J］.岩石力学与工程学报，2000，19(6):670-673.Wang Guangguo， Du Mingfang， Miao Xingcheng.Mechanism of compaction grouting and effect examination［J］.Chinese Journal of Rock Mechanics and Engineering，2000，19(6):670-673.(in Chinese)

［2］ 唐智伟，赵成刚.注浆抬动地层的机制、解析解及数值模拟分析［J］.岩土力学，2008，29(6):1512-1516.Tang Zhiwei，Zhao Chenggang.Mechanisms of ground heave by grouting and analytical solutions＆numerical modeling［J］.Rock and Mechanics，2008，29(6):1512-1516.(in Chinese)

［3］ Gonzalez C，Sagaseta C.Patterns of soil deformations around tunnels:application to the extension of Madrid Metro［J］.Computers and Geotechnics，2001，28(6/7):445-468.

［4］ Gollegger J.Numerical and analytical studies of the effects of compensation grouting［D］.Graz，Austria:Graz University of Technology，2001.

［5］ 侯艳娟，张顶立，陈峰宾.隧道施工下穿建筑物注浆抬动机制及预测研究［J］.岩石力学与工程学报，2011，30(12):2407-2415.Hou Yanjuan，Zhang Dingli，Chen Fengbin.Study of mechanism and prediction of grouting uplift in tunnel construction under crossing buildings［J］.Chinese Journal of Rock Mechanics and Engineering，2011，30(12):2407-2415.(in Chinese)

［6］ 李立新，童无欺，邹金锋.注浆抬动位移的随机介质理论预测方法［J］.铁道科学与工程学报，2013，10(5):47-51.Li Lixin，Tong Wuqi，Zou Jinfeng.Study on grouting uplift displacement prediction using stochastic medium theory［J］.Journal of Railway Science and Engineering，2013，10(5):47-51.(in Chinese)

［7］ 边学成，程 翀，王复明，等.高速铁路路基沉降高聚物注浆修复后动力性能及长期耐久性的试验研究［J］.岩土工程学报，2014，36(3):562-568.Bian Xuecheng，Cheng Chong，Wang Fuming，et al.Experiment study on the dynamic stability for the highspeed railway foundation rehabilitated by polymer injection technology［J］.Chinese Journal of Geotechnical Engineering，2014，36(3):562-568.(in Chinese)

［8］ 黄 炎.工程弹性力学［M］.北京:清华大学出版社，1982:23-95.

［9］ 吴家龙.弹性力学［M］.北京:高等教育出版社，1987:98-171.

［10］ 邹金锋，李 亮，杨小礼，等.劈裂注浆能耗分析［J］.中国铁道科学，2006，27(2):52-55.Zou Jinfeng，Li Liang，Yang Xiaoli，et al.Energy dissipation analysis for crack grouting［J］.China Railway Science，2006，27(2):52-55.(in Chinese)

［11］ Warner J.Practical Handbook of Grouting:Soil，Rock，and Structures［M］.New York:John Wiley ＆ Sons，Inc，2004.

［12］ 《岩土注浆理论与工程实例》协作组.岩土注浆理论与工程实例［M］.北京:科学出版社，2001:71-93.

［13］ 邹金锋，李 亮，杨小礼.劈裂注浆扩散半径及压力衰减分析［J］.水利学报，2006，37(3):314-319.Zou Jinfeng，Li Liang，Yang Xiaoli.Penetration radius and pressure attenuation law in fracturing grouting［J］.Journal of Hydraulic Engineering，2006，37(3):314-319.(in Chinese)

［14］ 杨 涛，薛伟辰.单调荷载下体外预应力钢-混凝土组合梁的受力性能［J］.江苏大学学报:自然科学版，2012，33(2):233-238.Yang Tao，Xue Weichen.Static behavior of steel-concrete composite beams prestressed with external tendons under monotonic loading［J］.Journal of Jiangsu University:Natural Science Edition，2012，33(2):233-238.(in Chinese)