积分方程法结合Ewald变换和栅格对称性分析周期性结构的散射特性

苏建勋，李增瑞

(中国传媒大学 信息工程学院，北京 100024)



积分方程法结合Ewald变换和栅格对称性分析周期性结构的散射特性

苏建勋，李增瑞

(中国传媒大学 信息工程学院，北京 100024)

摘要：本文提出空域积分方程法分析周期性结构。空域周期格林函数的计算通过改进的Ewald变换进行加速。利用周期性结构栅格的对称性简化了几何模型的尺寸，未知量大大减少，以致填充矩阵和求解MoM线性系统的时间大为减少。我们的方法跟目前已发表的文章和商业软件相比，更高效和精确。

关键词：频率选择表面(FSS)；周期格林函数(PGF)；Ewald变换；积分等式(IE)；栅格对称性(Lattice symmetry)

1引言

周期性结构目前广泛用于微波波段频率复用系统中的子反射面，以及用于构成复合雷达罩，在红外波段还能被用于极化器或者分束器以及可见光波段的太阳能吸收表面。除此之外，频率选择表面与雷达吸波材料(RAM)[1，2]结合的吸波体还被涂敷于飞行器表面用于RCS减缩。频率选择表面的单元形状比较多元化，近年来分形结构[3，4]也被应用到频率选择表面的单元设计中，使其具有多频谐振特性。

在过去30年，世界很多学者研究FSS等周期结构的分析方法。周期矩量法有一个问题就是周期格林函数收敛很慢，以致矩阵填充时间很长。过去很多人在谱域和空域里都做过很多的研究，尤其是Mittra等人。虽然周期格林函数计算速度上有了很大的改进，但是也无法跟最近几年兴起的新技术Ewald变换相比，Ewald变换能使得周期格林函数通过几项求和就能收敛。周期结构栅格(lattice)通常具有很好的对称性，但目前还没有相关的文献报道，利用栅格对称性简化几何模型。

本文详细地介绍了空域积分方程法(Spatial-domain IE)分析频率选择表面，利用改进的Ewald变换加速周期格林函数的快速收敛。同时利用栅格的对称性简化计算几何模型，使得未知量大大减少，实现了快速填充MoM矩阵和求解线性系统。跟目前已发表的文献和最新版本的商业软件比，本文的方法更高效和精确。

图1　双周期性结构

2积分方程与Ewald变换

2.1积分方程

完全导体(PEC)表面电场的切向分量为零，把边界条件强加于金属面S，可得电场积分方程(EFIE)[5]：

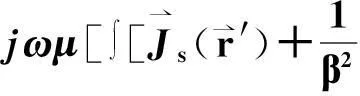
(1)

其中Gp为周期格林函数。基于三角片元的Rao-Wilton-Glisson (RWG)基函数应用于离散表面电流。

2.2改进的Ewald变换

(2)

其中

是互易栅格矢量。

其中Re(kzmn)≥0，Im(kzmn)≤0。

(3)

其中

(4)

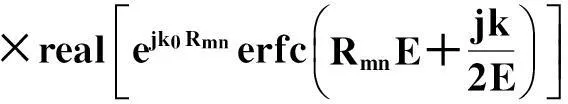
(5)

通过对两个序列的渐进性进行分析，优化撕裂因子可得：

其中H2是最大指数许可。在实际应用中，9项就可确保双序列收敛(即求和限由-1到+1)，PGF的误差值小于 0.1%。

3利用栅格对称性(Lattice symmetry)简化几何模型

以缝隙周期结构如图2为例。因为缝隙周期结构相对来说，复杂一些了，跟周期边界(PB)接触的那些三角网格要做一些特殊处理。

图2　矩形缝隙FSS

3.1平面波垂直入射

图3　场三角和源三角(红线：源三角的电流流向)

平面波垂直入射FSS，假设电场(E-field)方向沿X-轴(TEMx)。利用栅格的对称性可以把几何模型简化为原来的1/4。除了主源三角(primary source triangle)，其他三个源三角的坐标可以通过主源三角坐标的镜像(mirror)获得。四个源三角的电流扩展系数有如下关系：

I1=-I2=-I3=I4

(6)

电场积分方程(EFIE)的阻抗矩阵元素为

(7)

其中

四个源三角同时作用于一个场三角。fn1是主源三角n1的基函数；fn2，fn3和fn4分别为其他三个源三角(n2，n3，n4)的基函数。

贴片左右边缘(red line)上的三角必须分配半基函数(half-RWG basis function)，因为实际上有电流流过贴片的左右边缘。贴片的上下边缘没有电流，是开放边缘(open boundary edge)。

3.2平面波斜入射

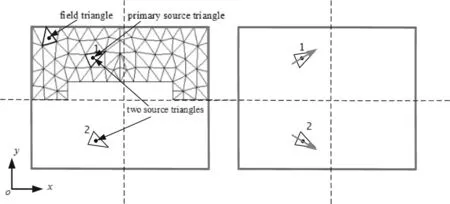
图4　场三角和源三角(红线：源三角的电流流向)

平面波斜入射FSS，假设电场(E-field)方向垂直于yoz-面。利用栅格的对称性可以把几何模型简化为原来的1/2。两个源三角的电流扩展系数有如下关系：

I1=I2

(8)

电场积分方程(EFIE)的阻抗矩阵元素为

(9)

贴片左边缘的三角和右边缘的三角对应地构成RWG基函数。贴片的上下边缘没有电流，是开放边缘(open boundary edge)。

4数值算例

4.1耶路撒冷十字架(Jerusalem Cross)贴片阵

图5　耶路撒冷十字单元

第一个例子是耶路撒冷十字架贴片阵列。单元的尺寸(mm)：w=1.9，l1=3.8，l2=5.7，a1=a2=15.2。图6为Floquet TEM mode的反射系数，电场沿X-轴方向(TEMx)。Ewald求和项设为9，进一步增加求和项，反射系数没有任何变换。为了确保整个频段里的仿真精度，整个单元结构剖分为320个三角。我们方法的仿真结果(Black line)跟FEKO的仿真结果(dashed line)和Mittra的谱域法结果(Blue line)很吻合。我们方法更高效，几何模型简化为原来的1/4，三角网格数目减少到80个，计算时间约为原来的1/4，内存为原来1/16

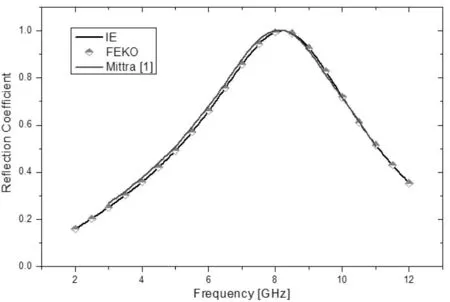
图6　反射系数

4.2十字架状的缝隙阵—红外光学滤波器(Quasi-Optical Filter)

下面分析一个红外光学带通滤波器，由十字架状缝隙组成的阵列，谐振频率为280GHz[8]。平面波垂直入射，电场沿X-轴方向(TEMx)。由于仿真频带很宽，Ewald求和项设为25(-2到2)，确保周期格林函数收敛。图8为传输系数的仿真结果，黑实线(Black solid line)为我们的仿真结果；红虚线(Black dot line)为参考文献[8]的仿真结果；蓝圈线为[8]的测试结果。我们方法跟测试结果吻合的很好。利用栅格对称性，几何模型简化为原来的1/4，如图8所示，三角网格数目由原来的2696个减少到674个。

图7　十字状缝隙

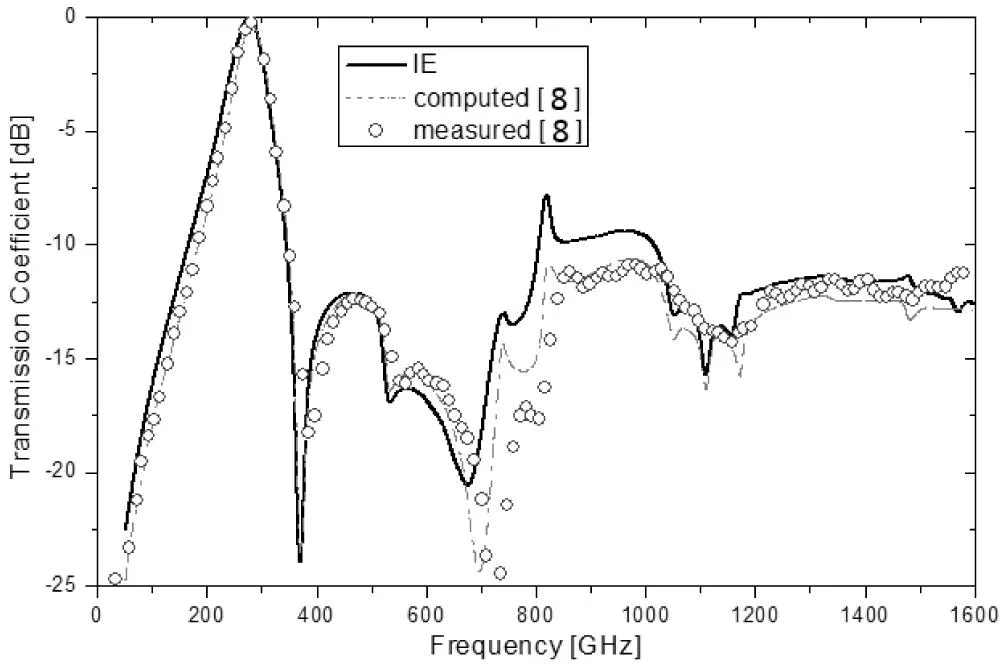
图8　传输系数

5结论

本文详细地介绍了空域积分方程法分析周期性结构，利用改进的Ewald变换加速周期格林函数的快速收敛。同时利用栅格的对称性简化计算几何模型，使得未知量大大减少，实现了快速填充MoM矩阵和求解线性系统。跟目前已发表的文献和最新版本的商业软件比，本文的方法更高效和精确。仿真表明，Ewald求和通常9项就能获得足够的精度，仿真结果跟其他文献的测试结果或数值结果吻合的很好，改进的Ewald变换是一种很好的加速周期格林函数收敛的方法。

参考文献

[1]R Mittra，C H Chan，T Cwik.Techniques for analyzing frequency selective surfaces—A review[J]. Proc IEEE，76(12)：1593-1615，Dec，1988.

[2]J B Pendry，A J Holden，D J Robbins，W J Stewart.Magnetism from conductors and enhanced nonlinear phenomena[J]. IEEE Trans Microw Theory Tech，47(11)：2075-2084，Nov，1999.

[3]D R Smith，W J Padilla，D C Vier，S C Nemat-Nasser，S Schultz.Composite medium with simultaneously negative permeability and permittivity[J]. Phys Rev Lett，84(18)：4184-4187，May，2000.

[4]A Boag，Y Leviatan，A Boag.Analysis of diffraction from doubly periodic arrays of perfectly conducting bodies by using a patch-current model[J].J Opt Soc Amer A，7(9)：1712-1718，Sep，1990.

[5]K E Jordan，G R Richter，P Sheng.An efficient numerical evaluation of the Green’s function for the Helmholtz operator on periodic structures[J]. J Comput Phys，63：222-235，1986.

[6]A W Mathis，A F Peterson.Efficient electromagnetic analysis of a doubly infinite array of rectangular apertures[J]. IEEE Trans Microw Theory Tech，46(1)：46-54，Jan，1998.

[7]F Capolino，D R Wilton，W A Johnson.Efficient computation of the 2-D Green’s function for 1-D periodic structures using the Ewald method[J]. IEEE Trans Antennas Propag，53(9)：2977-2984，Sep，2005.

[8]M Bozzi，L Perregrini，J Weinzierl，C Winnewisser.Efficient analysis of quasi-optical filters by a hybrid MoM/BI-RME method[J].IEEE Trans Antennas Propag，49(7)：1054-1064，Jul，2001.

(责任编辑：宋金宝)

Integral-equation Analysis of Periodic Structure Using

Ewald Transformation and Lattice Symmetry

SU Jian-xun，LI Zeng-rui

(School of Information Engineering，Communication University of China，Beijing 100024)

Abstract：In this paper，we present a space-domain integral-equation method for the analysis of periodic structures formed by three-dimensional (3-D) metallic objects arranged in a general skewed two-dimensional lattice.The computation of the spatial domain Green’s function is accelerated by the Ewald transformation.The geometric model is simplified by the lattice symmetry，so that the unknown is greatly reduced.Filling MoM matrix and solving linear system are greatly reduced.Our technique shows much higher efficiency when compared with available commercial software and the methods published at present.

Keywords：frequency selective surfaces (FSS)；periodic Green’s functions(PGF)；Ewald transformation；integral equations；lattice symmetry

作者简介：苏建勋(1982-)，男(汉族)，广东台山人，中国传媒大学博士后.E-mail：sujianxunjlgx@163.com

基金项目：国家自然科学基金项目(61331002，61201082)

收稿日期：2015-03-20

中图分类号：TN011

文献标识码：A

文章编号：1673-4793(2015)03-0024-05