正交异性矩形板固有频率的确定*

苏　铁　坚

(吉林建筑大学交通科学与工程学院，长春　130118)

正交异性矩形板固有频率的确定*

苏铁坚

(吉林建筑大学交通科学与工程学院，长春130118)

摘要：笔者应用最小余能原理的理论和方法对弹性正交异性矩形板进行动力分析，计算了结构的固有频率，对于剪力以及不同边界支承条件对正交异性板动力参数的影响进行讨论.

关键词：最小余能原理；弹性正交异性板；固有频率

0引言

在实际工程中，有许多构造上的正交异性(矩形)板结构.如建筑工程、桥梁工程或船舶工程中由交叉梁和连续矩形板构成的整体梁板结构；机械工程及航空工程中广泛使用的具有辗制方向的金属板、波纹板和加肋板等.分析这类正交异性板的动力问题，作为近似计算方法之一的最小余能原理显示出独特的优越性.尤其是在处理多种变形共存以及复杂边界条件下的振动问题时更为突出.

1基本原理与方法

对于弹性正交异性板，仍然采用与普通同性板相同的假设条件.为了计算和推导方便，假设正交异性板的两个弹性主方向与坐标方向(x , y方向)重合.

当板以频率ω作自由振动时，假设其振型函数为：

W=w(x,y)

所对应的板上的面分布横向惯性力集度为：

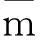
(1)

式中：D1，D2分别为弹性主方向(x,y方向)的抗弯刚度；Dk为板的抗扭刚度；μ1，μ2分别为板的主方向(x,y方向)的泊松比，且D3=D1μ2+2Dk[1].

对于每一种特定情况，由上式可确定满足平衡方程及力边界条件的振型函数，进而求出结构的弯矩(Mx，My)、扭矩(Mxy).由诸内力及振型函数表示的结构总余能为：

(2)

式中，第二个积分为剪力引起的应变能，δ为板的厚度，最后一个积分表示结构的动能.问题的位移边界条件(变形连续条件)应用最小余能原理：

(3)

2四边简支板的动力分析

2.1　固有频率的计算

如图1所示，当边长分别为a,b的四边简支板作自由振动时，其振型取为在x方向有m个正弦半波，在y方向有n个正弦半波，对应的固有频率为ωmn，采用一次近似计算.

图1 四边简支板模型

设振型函数为：

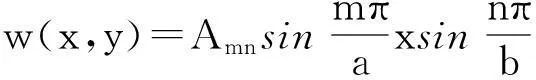
对应的面分布横向惯性力集度为：

将前两式代入平衡方程(1)中，求得振型函数为：

式中：

由惯性力引起的内力为：

(4)

对于同性板，固有频率

(5)

为该问题的精确解[3].

2.2　剪力对固有频率的影响

在问题2.1中加入剪力的影响.设m=n=1，按边长为a的方板计算，取惯性力作用下的剪力为：

(6)

式中：

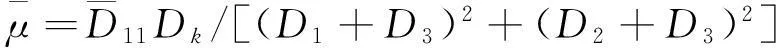
(7)

(8)

式中：

(9)

为剪力影响系数.对于同性板，有

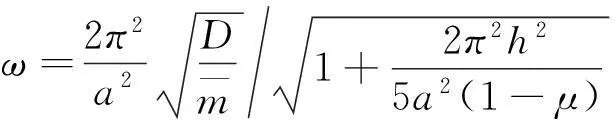
(10)

3不同支承条件下正交异性板的固有频率

3.1　一边固定，另三边简支

一边固定，三边简支、边长为a的正交异性方板，见图2，求固有频率.将问题简化成四边简支方板，对应原固定边界处有分布力矩作用，见图3.采用一次近似计算，设振型函数为：

由惯性力引起的内力均与问题2.1中的结果一致.

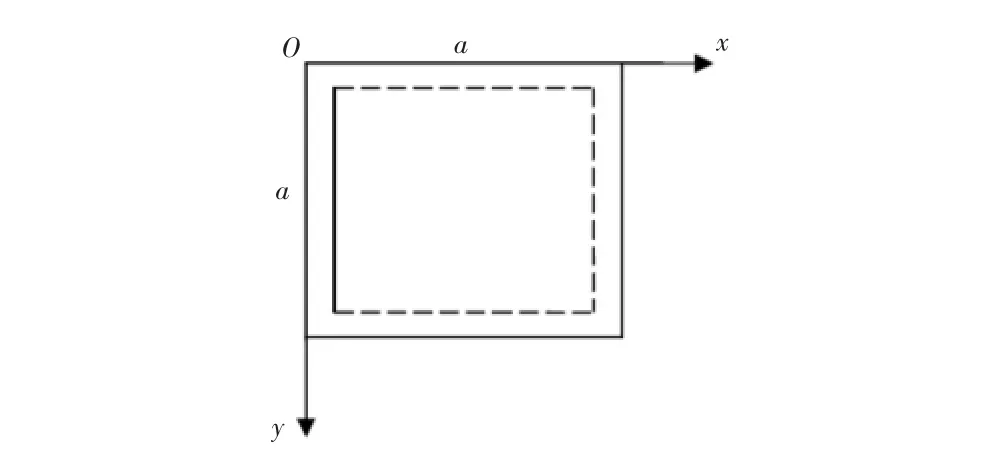
图2 一边固定，三边简支板模型

图3 简化后的简支板模型

设边界分布力偶m0引起的内力为：

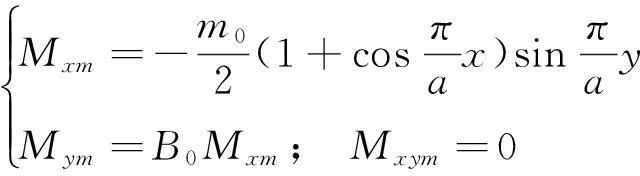
式中：B0=D2(1+μ1)/D1(1+μ2)为内力比例系数，对于同性板有B0=1.则板的总内力为：

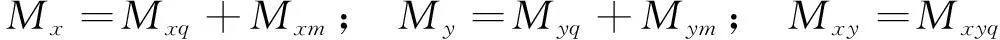
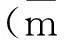
(11)

式中：

对于同性板有D0=D，其固有频率为：

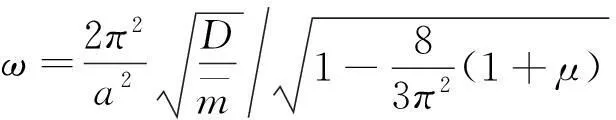
(12)

结果(μ=0.2)与问题精确解的误差为1.50%.

3.2　一对边固定支承，另两边简支

一对边(平行于y轴)固定支承，另两边简支、边长为a的正交异性方板，求结构的固有频率.将其简化为四边简支方板，对应原固定支承边界上有分布力偶作用的计算模型.由惯性力引起的内力与问题2.1相同，由边界力偶引起的内力取为：

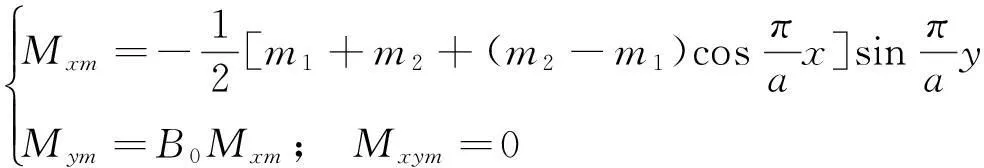
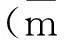
(13)

对于同性板，其固有频率为：

(14)

结果(μ=0.2)为问题的精确解[4].

参考文献

[1] 曹治杰,余传禧.正交异性板的计算[M].北京：中国铁道出版社，1983:2-6.

[2] 林家浩,曲乃泗,孙焕纯.计算结构动力学[M].北京：高等教育出版社，1989:167-170.

[3] 徐芝纶.弹性力学(第三版)下册[M].北京：高等教育出版社，2003:79-82.

[4] Warren C.Young Richard G.Bndynas.Roark’s Formulas for Stress and Strain (Seventh Ed)[M].New York:McGraw-Hill Companies,2002:764-766.

*基金项目：吉林省科技厅应用基础研究项目资助(201205056).

Determine the Natural Frequencies of Rectangle Orthogonal Plate

SU Tie-jian

(SchoolofCommunicationScienceandEngineering,JilinJianzhuUniversity，Changchun，China130118)

Abstract：In this paper, the minimum excess principle are used in dynamic analysis of rectangle orthogonal plate. The natural frequencies are calculated in detail, and the influences of shear and different Constraints on the natural frequency are discussed.

Keywords:minimum excess principle；rectangle orthogonal plate；natural frequencies

中图分类号：TU 311.3

文献标志码：A

文章编号：2095-8919(2015)06-0005-04

作者简介：苏铁坚(1957~),男,吉林省长春市人,教授.

收稿日期：2015-02-09.