基于自适应Memetic算法的多级多商品物流网络优化设计

张光平

（贵州电子信息职业技术学院 计算机科学系，贵州 凯里 556000）

1 引言

物流网络包含了物流网络中相互作用的组织和设施。物流网络的结构直接决定了物流网络的效率，与此同时，企业物流网络的好坏又在一定范围内代表企业的综合管理水平。因此，物流网络引起了众多研究者越来越多的关注，目前已成为物流系统设计中极为关键的一步。然而，当前的物流网络往往针对固定的三层或四层的单一商品流进行物流网络的设计，不能更好地适应多商品流或网络结构拉长的问题，若根据情况不断建立新模型，又增加了物流过程中的建模难度，使得物流配送过程效率低，成本高。

根据上述情况，本文提出了一种更符合实际的多级多商品物流网络结构，在建立与实际情况更符合的物流网络模型的基础上，采用群集智能的方法解决该模型的优化问题。所设计的多商品物流网络与优化模型可以根据多商品流的物流状况，最大化减少网络的存储费用、运输费用和建设费用等，设计出可解决一般性的多级多商品物流网络设计问题并含约束条件的优化模型，该模型适用于任意层的物流网络（实际应用中层级数不小于3），最后利用相应的算法框架解决该模型的优化问题。

2 多商品物流网络数学建模

物流网络是一个相互联系的组织和设施集合的结构，其目的是符合客户需要，提高企业竞争力。物流网络的优化能够给用户越来越多的依赖，越来越灵活的适应日益增长的需求。目前三级物流网络应用最为广泛，但只适用于节点数目少或者节点集中的地区。随着物流网络越来越复杂，商品流向少批量、多批次的方向发展，原来的物流网络会造成物流运输成本增加，运输频率提高，造成严重的经济损失。因此，企业迫切需要设计一种合理的多级多商品物流网络，可根据每一级物流网络的任务和设施条件有区别地设计物流网络。

图1 多商品物流网络

图1就是一种典型的多级物流网络。网络中选择合理的地点，再根据流量密度和交通运输方向来建立适当规模的物流节点，在节点处对集中到此的商品进行统一管理，最后通过最佳模式将商品运输至下一层节点，直到商品抵达目的地。

本文中多商品物流网络数学建模问题涉及变量定义如下[2]：

N：多级多商品物流网络的级数，实际问题中通常取N≥3；

：需求点i对商品l的需求量；

：第n(2 ≤n≤N)级的第i个物流网点的建设费用；

Wn：第n级的建设数目；

：第n级第i个网点流通和存储的能力；

：商品l在第n级第i个网点的存储费用；

：商品l从第n(n≤N-1)级第i个网点流到第n+1 级第j个网点的运输费用；

：商品l在第n级第i个网点的可变存储成本；

：第n(n≤N-1)级第i个网点处商品l的数量（流通量）；

：商品l从第n(n≤N-1)级的第i个网点流到第n+1级第j个网点的商品数；

Mn：第n级网点处产品的最大数目。

此外，定义二值变量Xn i代表是否决定修建第n级第i个网络（修建时为1，相反为0），实际中若第n级第i个网点的流通量=0，则=0，否则=1，L为商品数目。二值变量取为0 代表第n 级节点对商品l 的需求由第n+1 个级节点j决定，反之取1。

另外所做的假设如下：

（1）多层多商品物流网络末端需求点的数量必须小于企业生产的商品数目，也就是说，商品数满足市场的需求；换一种表示方式为：第n级第i个网点处是无穷大的。

（2）物流网点处不需要商品，也就是网点i处Vi为0。

（3）一个需求点处的商品只由一个网点提供。

（4）位于网络结构起始级的一个工厂只生产一种产品，若一个工厂生产多种产品，则该产品的物流网络起始点为对应的若干工厂。

由此可知，物流网络各级流通量为：

在多层多商品物流网络中，起点和终点的位置确定，设计该物流网络的过程就是每个节点的多重选址问题。换言之，就是在各种约束条件下选择最佳的中心地址，设计的目标是在最少的成本下满足用户要求。

3 多商品物流网络模型优化设计

在多级多商品物流网络的优化设计中，通常以总费用最低作为优化的目标函数。正常物流业务费用包括库存费用、运输费用、建设费用等。其中运输和库存的比重大。

（1）目标函数设计。多级多商品物流网络的费用主要包含库存费用、运输费用和建设费用：

①库存费用：库存费用含不变和可变库存费用。其中，不变库存费用为，可变库存费用可由鲍姆沃夫方法得到为，参数0 ≤θ≤1 的值和物流网络节点的规模相关。

②运输费用：商品从生产点到需求点过程中产生的所有费用，计算公式为

③建设费用：建设费用产生在网络建设的初期，一次性支付，是建设网络节点的基本费用，其计算公式为

（2）约束条件设计。设计物流网络的过程中，需要满足以下的约束条件：

①网络节点的能力约束。节点的能力范围是任意中间的节点，经过其的商品数换成的能力之和不能超过其处理的能力，也就是：

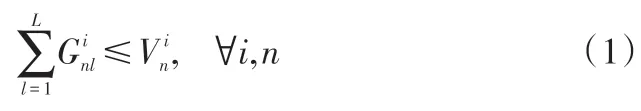
②网络节点的数量限制。出于对前期建设费用的考虑，需要限制网络节点的数目，约束条件为：

③物流网点的等量限制。对于任意的物流网络节点，从上级流入的商品数应等于流向下级的商品数。该限制可以写成：

④非负限制。一些变量如、等不能为负数。

（3）多商品物流网络优化模型构建。假设建立物流网络的总费用为Ψ，该优化模型为：

4 基于自适应Memetic 算法的多商品物流网络优化设计实现

1975 年J.Holland 教授提出遗传算法，该算法被广泛用在优化领域，尤其适用于较大规模的优化组合问题。遗传算法遵循“适者生存”的原则，指导染色体的逐代进化（含选择、交叉和突变等），实现个体适应性的提高。其特点是可直接对结构对象操作，没有求导和函数连续性的约束，不需要辅助信息；易于并行化和全局寻找最优解的能力；通过概率化的寻优方式，具有内在的启发式随机搜索的特点，可以自适应地搜索，不需要确定的规则。然而，遗传算法存在运算时间长、可能陷入局部最优的缺点。Memetic 算法是最近一种非常有效的群集智能优化算法，它将遗传算法的全局搜索与局部搜索相结合，其数学模型定义如下：

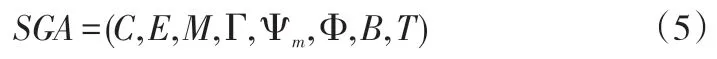
其中：

C：个体的编码方式；

E：个体适应度的评价函数；

M：种群大小；

Γ：交叉算子；

Ψm：变异算子；

Φ：选择算子；

Β：局部搜索算子；

T：终止条件。

由于多级多商品物流网络费用函数的优化是一个非常复杂的问题，本文提出基于自适应算子的新的自适应Memetic算法。自适应算子具体介绍如下：

（1）自适应度值调整。Memetic 算法不断收敛时，继续优化的困难增大，使得最优解附近摇摆不定。为提高选择力，应放大个体适应度值。标定适应度值公式:

其中，f为初始适应度值，f'为调整后的适应度值，fmax和fmin分别为适应度值的上下界，0 ＜α＜1。

由图2可知，角度α随着fmax和fmin的差值增大而变小，防止了超常个体过多，缩小了标定后的适应度值变化范围；反之α变大，拉开群体中个体之间的差距，增大标定后的适应度值变化范围，以尽快得到最优解。适应度值随实际情况发生变化，加快了获得问题最优解的速度。

图2 标定后的适应度值随种群适应度差值的变化关系

（2）群体多样化。若不限制较大概率成为局部最优解的高适应度值个体，算法在初始设置不合理的状况下容易陷入局部最优。为解决这类问题，本文引入群里多样化的定义。该方法是在对个体选择之前，比较每两个个体在相同地方的相同基因的数目，定为R，将R是否大于个体的一般作为是否相似的分界点[6]。选择不相似的个体组合到一起构成新群体。

综上所述，所设计的自适应Memetic 算法的流程如图3所示。

图3 自适应Memetic算法流程图

将上述自适应Memetic算法应用于物流网络模型，可利用自适应Memetic设置多层多商品网络优化模型的初始参数，分析每一种商品并按需求配送。目前的算法只针对3级物流网络，而对于求解多级多商品的物流网络初始解，需要使用更多空间和多次迭代，也就是说按照先前的算法，计算第一、二级组成的物流网络的初始解，再将第二级中的物流网点作为假定用户点，再计算第二、三级组成的多商品物流网络的初始解，一直划分与迭代，直到解出所有网络节点的分配决策变量。其框架为：

（1）划分寻优空间，按个体适应度值的大小排序。

（2）计算自适应适应度，选出适应度值大于个体平均适应度的个体。

（3）除去最高适应度个体的相似个体。

（4）重复（3），选出与适应度值最高的个体不相似的个体组成新群体。

（5）若群体规模不满足规定，那么将除去的个体按适应值大小依次填补所缺数量。

（6）判断是否结束，若是则结束，否则将前规定值个体所在的字符串子空间作为新的寻优空间，进行步骤（1）。若全局最优解在边界处，则移动寻优空间再进行步骤（1）。

下面通过实证分析验证方法的有效性，在本案例中N=3，

在本文所提出的Memetic 算法中，种群数目M为150，交叉为简单交叉，交叉概率为0.7，变异为单点变异，变异概率为0.4，初始的种群采用随机初始化，局部搜索采用最速梯度下降，在相同的规模下对比了所提出的自适应Memetic算法与标准遗传算法的性能。寻找到最优解所需要的最大迭代次数Max与最优解对应的目标函数见表1。从结果可以看出，自适应Memetic 算法相比标准遗传算法，不仅能够找到更优的解，而且具有更快的收敛速度。

表1 网络优化结果对比分析

5 结语

随着企业规模的增大，其商品的配送方式和客户的定位也更复杂化，为了降低物流成本，且满足企业的需要，设有约束条件的多级多商品物流分配网络应运而生。本文设计了一种新的基于自适应Memetic算法的多商品物流网络。一方面，自适应Memetic 算法框架可有效解决带有约束条件的多级网络寻找全局最优解的问题；另一方面，算法中的局部搜索与自适应算子大大降低了群集算法陷入局部极值点的可能性，并且加速了搜索，使得快速高效的实际复杂物流网络的优化成为可能，因此在多商品物流网络设计上具有较好的应用前景。

[1]徐磊.基于遗传算法的多目标优化问题的研究与应用[D].长沙:中南大学,2007.

[2]张哲.基于遗传算法的多商品物流网络设计的研究[D].大连:大连海事大学,2012.

[3]高自友,孙会君.现代物流与交通运输系统[M].北京:人民交通出版社,2003.

[4]Gen M,Cheng R.Genetic algorithms and engineering optimization[M].New York,N Y,USA:John Wiley & Sons,2000.

[5]曹友道.基于改进遗传算法的应用研究[D].合肥:安徽大学,2010.

[6]Jaramillo,Bhadury, Batta.On the use of genetic algorithms to solve location problems[J].Computers&Operations Research,2002,29(6):761-779.