液压衬套与液阻悬置作用机理的对比分析*

杨超峰　殷智宏†　吴川永　上官文斌

(1.华南理工大学 机械与汽车工程学院， 广东 广州 510640； 2. 上汽通用五菱汽车股份有限公司， 广西 柳州 545007)

液压衬套与液阻悬置作用机理的对比分析*

杨超峰1殷智宏1†吴川永2上官文斌1

(1.华南理工大学 机械与汽车工程学院， 广东 广州 510640； 2. 上汽通用五菱汽车股份有限公司， 广西 柳州 545007)

摘要：建立了液压衬套与液阻悬置的集总参数模型，比较了两者的连续方程、动量方程及传递力方程.通过分析对应的等效机械模型，对比了惯性通道内液体的等效质量及阻尼的放大倍数.推导了惯性通道内流量响应及液室内压强响应的方程，阐释了两者作用机理的差别.在谐波激励下，对比了液压衬套与液阻悬置特征参数点及阻尼比取值范围的不同.研究表明，通过改变液压衬套的体积柔度参数，可使液压衬套的模型适用于液阻悬置的动态特性分析.最后通过实验验证了计算分析的正确性.

关键词：液压衬套；液阻悬置；集总参数模型；动态分析；统一模型

为了控制来自发动机、变速器、路面及车轮的不平衡等干扰激励引起的振动及噪声，发动机、变速器一般通过橡胶悬置或液阻悬置与车身或副车架相连接，悬架控制臂一般通过橡胶衬套或液压衬套与车身相连接.橡胶悬置、橡胶衬套、液阻悬置(HEM)、液压衬套(HDB)统称为橡胶隔振器[1-3].由于要限制振幅及快速衰减振动，要求橡胶隔振器应具有大刚度、大阻尼特性.同时，又要控制高频、小振幅振动所诱导的高频噪声，隔振器应具有小刚度、小阻尼特性[1].但由于典型的橡胶悬置或橡胶衬套因橡胶材料的滞后角一般在3°~15°之间[1-2]，难以满足设计需求.通过在橡胶衬套或悬置中封装液体，得到的液阻隔振器具有大阻尼特性，可以满足快速衰减大振幅振动的要求[2-5].

HDB与动力总成中的HEM不同点在于其两个液室均为工作液室，即两个液室中的压力均很大，而HEM中下液室的橡胶膜很薄，且直接与大气相通，液室内的压力较小[3-4].潘孝勇[5]认为HDB在阻尼方向上的刚度稍大于HEM，其峰值阻尼频率的可调节范围较大，开发难度大于HEM，但并没有给出理论的对比模型.Chai等[6-8]认为HDB虽然工作原理上类似于发动机HEM，但它们的应用、结构及动态特性并不相同，但作者并没有对两者之间的区别进行解析分析.由上所述，目前对HDB与HEM之间的区别及转换的作用机理分析得较少.

文中通过建立的集总参数模型，对比了两者的连续方程、动量方程及力的传递方程.采用解析的方法对比了两者不同性能的差别，并阐释了两者作用机理的不同.对特征参数的不同进行了分析.通过改变HDB的参数，实现了两种液阻隔振器的转换.计算结果与实验所采用的方法相吻合.为采用HDB替换HEM的初期开发及设计提供一种选型的依据.

1HEM及HDB集总参数模型对比

封液式减振器被认为是性能最好的被动式橡胶隔振器，HEM已经发展到惯性通道-解耦盘-节流盘式HEM[3].但由于HDB结构内部没有足够的空间布置解耦装置，单惯性通道式HDB虽然在工作原理及结构上与HEM有一定的相似性，但它们的应用、结构及动态特性有较大的差别[8-10].液阻橡胶隔振器的动特性一般采用动刚度与滞后角进行评价[3].

1.1　液阻悬置的集总参数模型

由文献 [3]中所示的HEM的结构示意图，可得到惯性通道式HEM的集总参数模型，如图1(a)所示，图中参数的定义与文献[10]中相同.其中液体的连续方程、动量方程及传递力方程可参考文献[10].

图1　HEM与HDB的集总参数模型Fig.1　Fluid system models of HEM and HDB

基于假设，忽略非线性流量阻尼的影响，通过Laplace变换，可得到HEM的复刚度的表达式[10]：

(1)

式中,Krm、Brm分别为橡胶主簧的动刚度及阻尼系数,Apm为橡胶主簧的等效活塞面积；K1m、K2m表示上、下液室的体积刚度，Iim为惯性通道内液体的惯性系数，Ri1m为惯性通道内液体的线性的流量阻尼系数.

1.2　液压衬套的集总参数模型

HDB的集总参数模型如图1(b)所示.图中p1m(t)、p2m(t)分别为两液室内的压力波动量；在压力的作用下，上下液室的膨胀特性采用体积柔度C1m、C2m表示；Krb、Brb分别为橡胶主簧的动刚度及阻尼系数；Ap1b、Ap2b分别为橡胶主簧泵液的等效活塞面积；P1b(t)、P2b(t)分别为两液室内的压力波动量；在压力的作用下，两液室的膨胀特性采用体积柔度C1b、C2b表示；K1b、K2b分别为体积刚度；Qib(t)为液体流径惯性通道的流量；lib为惯性通道的长度；Aib为惯性通道的横截面积；xib(t)为液柱相对壁面的位移.内管上承受正弦位移激励为xrb(t)=Xrbsinωt，动反力为FTb(t).

由液体的连续方程，得

(2)

由通道内液体的动量方程，得

(3)

式中：Iib为惯性通道内液体的惯性系数；Ri1b、Ri2b分别为惯性通道内液体的线性与非线性的流量阻尼系数，其值与通道的横截面形状、液体的黏度及管道壁面的粗糙度等参数有关[8].Iib、Ri1b及Ri2b的物理意义及定义与HEM中Iim、Ri1m及Ri2m类同[8].

衬套固定端动反力[2,10]的表达式为

(4)

同理，由式(2)-(4)，得到HDB复刚度的表达式为

(5)

1.3　集总参数模型的对比

由HEM及HDB液体的连续方程可知，HDB内管受到的位移激励xrb，同时影响两液室的体积柔度C1b与C2b.而HEM的顶端受到位移激励xrm作用，下液室的体积柔度C2m对液阻悬置动特性的影响较小[3].

假设HDB具有对称的橡胶主簧，则构成两液室的形状类似，可认为橡胶主簧泵液的等效活塞面积Ap1b与Ap2b相同，且两液室的体积柔度C1b与C2b相等，令式(2)中两式相加，可得到

P1b(t)+P2b(t)=0

(6)

式(6)表明两液室内的压强大小相同，但方向相反.而HEM下液室内的压强与上液室内的压强相比较小，下液室内的压强与大气压接近.

对比HEM与HDB的动量方程可知，当采用同种类型的混合防冻液体，且悬置与衬套惯性通道的参数(长度、横截面积及局部损失)相同时，则对应两者惯性通道内液体的动量方程相同.

对比HEM与HDB的传递力方程可见，HEM内部的液体主要通过上液室对固定端起作用，而HDB内两液室内的压强对FTb(t)都有贡献.

所采用的HEM与HDB相关参数如表1所示，Apmd为HEM下液室的等效活塞面积，但是由于下液室的体积柔度较大，可认为Apmd≈0，其对FTm(t)的影响忽略不计.由表中的参数可得到HEM及HDB的动特性如图2所示.

表1　几何材料参数Table 1　Geometric and material parameters

由图2(a)可知，与HEM的动刚度相比，HDB动刚度的陷波峰值降低，出现陷波峰值的频率增大；但HDB动刚度的最大峰值增大很多，出现最大峰值的频率也增加.

由图2(b)可知，与HEM的滞后角相比，HDB的滞后角的峰值增高，出现峰值的频率增加，并且滞后角的带宽增加，表明HDB可在较宽的频率范围内提供较大的阻尼.

图2　HEM与HDB动特性对比图Fig.2　Comparison of dynamic characteristics between HEM and HDB

2HEM与HDB性能的对比

由于液阻橡胶隔振器被称为“速度放大型吸振器”[11]，橡胶隔振器的等效质量及阻尼的放大倍数是其性能的表征参数.液室内的压强响应量及惯性通道内液体流量的响应量对液阻橡胶隔振器动特性的影响较大，且低频下液阻橡胶隔振器的陷波峰值、液柱的共振频率及阻尼是设计的重点.本节中采用定量分析的方法对两种液阻隔振器参数的放大倍数、液柱的共振频率、阻尼比、通道内的流量响应、液室内压强响应量及特征参数点进行分析.

2.1　等效质量及阻尼放大倍数的比较

HEM及HDB惯性通道的横截面积只是对应等效活塞面积面积的几十分之一，由液体的连续性可知，惯性通道内液体的运动的速度应该是液室内液体速度的几十倍，这种液力机构的动力放大作用类似于杠杆机构.由于惯性通道内液体速度被放大，可认为通道内液体运动的大部分动能等效集中在这一小质量的惯性液柱上，液室内的液体只具有液力传递的作用，而对振动衰减的贡献较小.所以这两种液阻橡胶减振器都可称为“速度放大型吸振器”，或“惯性阻尼增强器”[12].

由以上分析，建立低频、大振幅激励下HEM与HDB的等效机械模型，如图3所示.图3(a)中，k1m为上液室的等效线性刚度，k2m为下液室的等效线性刚度，bim为惯性通道内液体的等效阻尼[13].图3(b)中，k1b、k2b分别为两液室的等效线性刚度，bib为衬套惯性通道内液体的等效阻尼[6-8].

由图3中两种液阻橡胶隔振器的等效机械模型，可得到HEM及HDB参数通道内液体质量及阻尼的放大倍数[13],如表2所示.

图3　HEM与HDB的等效机械模型Fig.3　Analogous mechanical models of HEM and HDB

表2　参数的放大比率Table 2　Amplification ratios of parameters

表2中，mimo、bimo分别为HEM惯性通道内液柱基于物理表达的质量与阻尼,mime、bime分别为HEM惯性通道内液柱的等效质量与阻尼,mibo、bibo分别为HDB惯性通道内液柱基于物理表达的质量与阻尼,mibe、bibe分别为HEM惯性通道内液柱的等效质量与阻尼[13].Aibe为惯性通道的等效横截面积,

(7)

如果采用表1中参数，则HDB与HEM等效的质量与阻尼的比值λ为

(8)

式(8)表明，采用文中的参数，HDB与HEM等效的质量与阻尼相同，表明放大倍数相同.但当HDB的体积柔度改变时，两者的等效质量与阻尼并不一定相同，放大倍数也有所不同.

2.2　通道内液体的固有频率及阻尼比的比较

HEM惯性通道内液柱的共振频率ωnm及无量纲阻尼比ζm的表达式[14]为

(9)

将式(2)代入式(3)，可得HDB惯性通道内液体的标准无量纲受迫振动方程：

(10)

式中,ωnb为HDB惯性通道内液柱的共振频率,ζb为HDB的无量纲阻尼比,F0b为强迫系数.ωnb与ζb的表达为

(11)

式(9)与(11)表明,HDB与HEM惯性通道内液柱的共振频率和阻尼比与液体的物理参数(密度、动力粘度等)、惯性通道的几何参数(长度、横截面积等)及两液室的体积刚度都密切相关，并且两液室的体积刚度为并联关系.

如果假设

(12)

2.3　通道内流量响应量的对比

通过Laplace变换，可得到HEM惯性通道内液体的流量随振幅变化的方程：

(13)

由式(2)和(3)，同理可得到HDB惯性通道内液体的流量随振幅变化的方程：

(14)

由图4可见，两种液阻隔振器惯性通道内流量的响应与频域下单自由度的稳态谐波振动曲线相类似.由图4(b)可知，HEM的液柱的无阻尼共振频率约为11 Hz，而HDB液柱的无阻尼共振频率约为15 Hz.在达到共振频率之前，通道内液体流量的响应运动与激励位移同相；当液体流量响应的滞后角达到-90°时，此时流量响应所对应的频率值与两种液阻隔振器的共振频率值相同；当激振频率值大于所对应的固有频率值后，流量响应与激振位移激励反向.又如图4(a)所示，两种液阻隔振器通道内流量的响应量振幅急速减小，表明惯性通道内的流量减小，通道趋于“锁止”.可见，通道内流量响应量的变化改变了两种液阻隔振器液室内压强差，进而影响两者的动特性.

图4　HEM与HDB动特性与液体流量响应量的对比Fig.4　Comparisons between response of volume and dynamic performance of HEM and HDB

由以上分析可知，与HEM相比，HDB通道内流量响应量达到峰值的频率增大，且峰值变大.在同等频率下，HDB通道内流量响应量的滞后角较小.

2.4　液室内压强响应量的对比

通过Laplace变换，可得到HEM上、下液室内压强随振幅变化的方程为：

(15)

由式(2)和(3)，同理可得到HDB两液室内压强随激励振幅变化的方程：

(16)

图5为HEM与HDB的动刚度与液室内压强响应量的对比，又由于K1m≥100K2m,由式(15)可知，HEM下液室内的压强响应量与上液室内的压强响应量相比较小，图5验证了式(15)的正确性.图5可知，HDB上、下液室的压强响应量相同，也验证了式(16)的正确性.

图5　HEM与HDB的动刚度与压强响应量的对比

Fig.5Comparisons between response of pressure and dyamic stiffenss of HEM and HDB

由图5可知，HEM上液室的压强响应量对HEM的动特性贡献最大，在8 Hz邻近，上液室的压强响应振幅还相对较小，在频率为8~11 Hz的范围内，压强急剧增大，在频率为12 Hz邻近时达到最大，表明由于通道内液柱在此频率段的反向运动，强迫大量液体涌入上液室，使上液室内压强增大.当频率大于18 Hz时，由于惯性通道的“锁止”，通道内的流量减小，上液室内的压强降低到一定水平.

由图5可见，HDB两液室的压强响应量对HDB的动特性贡献都较大，在12 Hz邻近，两液室的压强响应振幅还相对较小，但在频率为12~14 Hz的范围内，压强急剧增大，在频率为15 Hz邻近时达到最大，表明由于通道内液柱的反向运动，使两液室内的压强都增大.当频率大于25 Hz时，由于惯性通道的“锁止”，通道内的流量减小，上液室内的压强趋近于定值.

综上所述，与HEM上液室的压强响应量相比，HDB两液室的压强响应量出现峰值的频率增大.当惯性通道“锁止”后,HDB趋向的定值较大.

2.5　特征频率点的对比

2.5.1液阻悬置的特征频率点

(17)

(18)

由式(18)，又由于ω≥0，可得到[15]

(19)

(20)

而当式(19)成立时，有

(21)

图6　HEM存储动刚度的特征参数Fig.6　Key frequency parameters of complex dynamic stiffness of HEM

(22)

由式(20)可得

0<ζm≤1/2

(23)

上式即为存储动刚度具有陷波峰值的条件.

2.5.2液压衬套的特征频率点

将式(11)代入方程式(5)，通过变换，可得到HDB复刚度的表达：

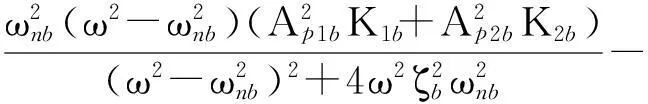
(24)

忽略Brb的影响，令

(25)

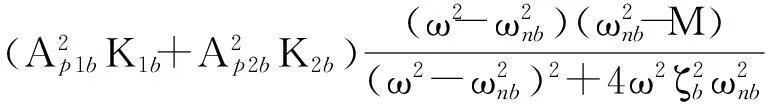
(26)

(27)

(28)

又由于ω≥0，可得到

(29)

(30)

(31)

同理，由上述特征频率点及特征参数的表达，根据实验数据，可对HDB的参数进行辨识.

当式(29)成立时，有

(32)

图7　HDB存储刚度的特征参数Fig.7　Key frequency parameters of complex dynamic stiffness of HDB

(33)

(34)

但当两橡胶主簧的等效活塞面积Ap1b与Ap2b相等时，M等于0，则阻尼比ζb的取值与式(23)相同.

由上所述，通过计算分析可见，当两种液阻隔振器采用同样的参数，两者的放大倍数、液柱的共振频率、阻尼比、通道内的流量响应、液室内压强响应量及特征参数点的解析表达类似，所以通过改变HDB特定的物理参数，可实现两者模型的统一.

3液压衬套与液阻悬置动特性的转换

将式(5)进行变换，可得到HDB复刚度的另一种形式的表达式：

(35)

(36)

由上式可见，若假设

(37)

根据式(37)，当HDB上部液室的体积刚度变小时，由式(36)可知，HDB的复刚度与HEM的复刚度相同，这时两种液阻橡胶减振器的动特性表达相同.

HDB的动特性随C2b的变化如图8所示，由图可知:随着C2b的增大，动刚度的陷波峰值增大，陷波峰值频率减小；最大动刚度峰值降低，产生最大峰值的频率减小.同时滞后角的峰值降低，峰值频率变小.当C2b=50C1b时，HDB的动特性几乎与HEM相同，当倍数增大到100时，改变并不明显.当C2b与C1b的比值大于50后，HDB的动特性与HEM的动特性相同.采用解析分析得到的结论与所采用方法与文献[4]中所采用的改型的HDB型悬置的设计方法相吻合，表明了理论分析的正确性.

当C2b与C1b的比值大于50后，在第2节中的两种液阻橡胶隔振器的参数性能近似相同.表明通过改变HDB的体积柔度的大小可实现两种液阻橡胶隔振器模型之间的转换.

图8　HDB动特性随C2b的变化Fig.8　Influence ofC2bon dynamic characteristic of HDB

4结论

(1)通过比较集总参数模型，认为HDB虽然工作原理上类似于发动机HEM，但两者的作用机理并不相同，只有两者液室的体积柔度之比大于50时，才可以得到类似的动态特性.在两者同等参数情况下，HDB的动刚度在较高的频率下具有较低的陷波峰值.

(2)采用定量分析的方法，与HEM进行比较，HDB惯性通道内液体的等效质量与阻尼放大倍数近似相同，但HDB的内液柱的共振频率较大；并且HDB惯性通道内液体流量响应量及压强响应量增大；采用计算的方法，对比了特征参数的不同，并得到存储动刚度具有陷波峰值的阻尼比的范围，认为当HDB的结构不同时，两者阻尼比的取值可以相同.

(3)通过解析分析，采用改变HDB液室体积柔度的方法，实现了两种液阻隔振器模型之间的转换，所采用方法与文献[4]中所采用的改型HDB式悬置的设计方法相吻合，表明了结论分析的正确性.

参考文献：

[1]Bernd Heißing,Metin Ersoy.Chassis handbook [M].Springer:Science & Business Media,2010.

[2]上官文斌,徐驰.汽车悬架控制臂液压衬套动态特性实测与计算分析 [J].振动与冲击,2007,26(9):7-10.

Shangguan Wen-bin,Xu Chi.Experiment and calculation methods of the dynamic performances for hydraulic bushings used in control arms of a suspension [J].Journal of Vibration and Shock,2007,26(9):7-10.

[3]Shangguan Wen-bin.Engine mounts and powertrain mounting systems:a review [J].Vehicle Design,2009,49(4):237-258.

[4]Müller Michael,Eckel Hans-Gerd,Leibach Markus,et al.Reduction of noise and vibration in vehicles by an appropriate engine mount system and active absorbers [J].SAE Technical Paper,1996:960185.

[5]潘孝勇.橡胶隔振器动态特性计算与建模方法的研究[D].浙江:浙江工业大学机械工程学院,2009.

[6]Chai Tan,Jason T Dreyer,Rajendra Singh.Time domain responses of hydraulic bushing with two flow passages [J].Journal of Sound and Vibration,2014,333(3)：693-710.

[7]Tan Chai,Jason T Dreyer.Rajendra Singh.Transient response of hydraulic bushing with inertia track and orifice-like elements [J].SAE Technical Paper,2013-01-1927.

[8]Tan Chai,Jason T Dreyer,Rajendra Singh.Dynamic stiffness of hydraulic bushing with multiple internal configurations [J].SAE Technical Paper,2013-01-1924.

[9]Yasuo Miyamoto,Sou Nakamura.Study of hydro bush for reduction of harshness and road noise [J].Review of Automotive Engineering,2005,26(1):33-40.

[10]Shangguan Wen-bin,Lü Zhen-hua.Modeling of a hydraulic engine mount with fluid structure interaction finite element analysis [J].Journal of Sound and Vibration,2004,275(1/2):193-221.

[11]Sugino M,Abe E.Optimum appliction for hydro-elastic engine mount [J].SAE Technical Paper,1986:861412.

[12]Singh Rajendra,Kim G.Linear analysis of automotive hydro-mechanical mount with emphasis on decoupler characteristics [J].Journal of Sound and Vibration,2002,158(2):219-243.

[13]Song He,Rajendra Singh.Estimation of amplitude and frequency dependent parameters of hydraulic engine mount given limited dynamic stiffness measurements [J].Noise Control Engineering Journal,2005,53(6):271-285.

[14]Aaron A Geisberger.Hydraulic engine eount eodeling parameter identication and experimental validation [D].Ontario:School of Mechanical Engineering of University of Waterloo,2000.

[15]Hwa Lee Jun,Kwang-Joon Kim.An efficient technique for design of hydraulic engine mount via design variable-embedded damping modeling [J].Journal of Vibration and Acoustics,2005,127:93-99.

Comparison of Working Mechanisms of Hydraulic Damped Bushings and Hydraulic Engine Mounts

YangChao-feng1YinZhi-hong1WuChuan-yong2ShangguanWen-bin1

(1.School of Mechanical and Automotive Engineering,South China University of Technology,Guangzhou 510640,Guangdong,

China;2. SAIC-GM-Wuling Automobile Co.,Ltd., Liuzhou 545007,Guangxi,China)

Abstract:First,the lumped parameter models of hydraulic bushings and hydraulic engine mounts are established,and the two hydraulic devices are compared in terms of the continuity equation,the momentum equation and the transfer force equation. Next, by analyzing corresponding equivalent mechanical models,both the equivalent masses of the liquid in inertia channels and the magnification of the damping of the two hydraulic devices are compared.Then, the equations of the pressure and flow response of the two hydraulic devices are derived and compared to interpret the difference in the working mechanisms of the two hydraulic devices.Moreover,under a harmonic excitation,the feature parameter and damping ratio of the two hydraulic devices are extracted and compared.It is found that changing the flexibility parameter of the hydraulic bushings can make the model suitable for the dynamic performance analysis of the hydraulic engine mounts.Finally,the proposed models and the analysis methods are proved to be correct by an experiment.

Key words:hydraulic bushing;hydraulic engine mount;lumped parameter model;dynamic analysis;unified model

中图分类号：TH 113；U 464

doi:10.3969/j.issn.1000-565X.2015.08.013

文章编号：1000-565X(2015)08-0082-09

作者简介：杨超峰(1981-)，男，博士生，主要从事液阻橡胶隔振器设计、车辆振动噪声分析与控制、汽车系统动力学等的研究.Email： ychf8130@163.com†通信作者： 殷智宏(1982-)，女，博士，讲师，主要从事汽车振动噪声分析与控制、汽车动力学、橡胶隔振、悬架系统设计与主动控制研究.E-mail: mezhyin@scut.edu.cn

*基金项目：国家自然科学基金青年基金资助项目(51305139);华南理工大学中央高校基本科研业务费专项资金资助项目(2013ZM0016)

收稿日期：2014-10-09

Foundation item: Supported by the National Natural Science Foundation for Young Scholars of China(51305139)