基于递归趋势调整的单位根检验

江海峰，杨海文

（1.安徽工业大学商学院，安徽 马鞍山243001；2.江西财经大学信息管理学院，南昌 330013）

0 引言

众所周知，单位根检验不仅包括单位根项本身的估计，还涉及到漂移项、趋势项估计及其经济意义解释，为使参数意义更为明确，Bhargava(1986)将数据生成的趋势项和单位根过程分离，提出如下数据生成过程：

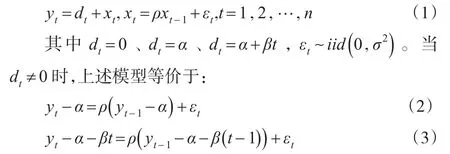
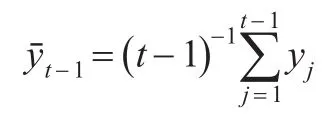
并检验假设 H01:ρ=1和联合假设 H02:ρ=1，α=β=0。然而，对于此类数据生成的递归趋势调整单位根检验尚没有文献研究，受到上述递归趋势调整模式研究的启发，本文也从递归趋势调整角度研究数据生成为dt=0的单位根过程而估计与模型（4）相对应的单位根检验量分布，并与经典DF检验量比较检验水平和检验功效。

1 递归趋势调整单位根检验量分布

为讨论这类模型，本文采用类似Bhargava(1986)的做法，估计如下模型：

2 蒙特卡罗模拟分析

为得到上述基于递归趋势调整单位根检验量有限样本下的分位数，下面进行蒙特卡罗模拟分析。设定模拟次数为50000次，为降低分位数的随机性，将该过程进行50次，取50次分位数的平均值作为最终的模拟结果。表1给出5种样本常见分位数的模拟结果，其中每个样本中第一行和第二行是分别与式（8）和式（9）对应检验量的分位数。和同种条件下的经典DF检验量相比，分位数明显偏大。模拟显示，当 ρ=1时，表1中5种样本单位根项ρ基于递归趋势调整式（7）估计的平均值分别为0.919、0.959、0.979、0.992和0.996，而根据式（4）得到 ρ的平均值分别为0.647、0.810、0.902、0.959和0.979，显然，正是由于采用了递归趋势调整估计方法，消除了存在于经典DF模式中解释变量与扰动项之间自相关问题，因此降低了估计偏差，这从估计角度说明了递归趋势调整方法的优越性。

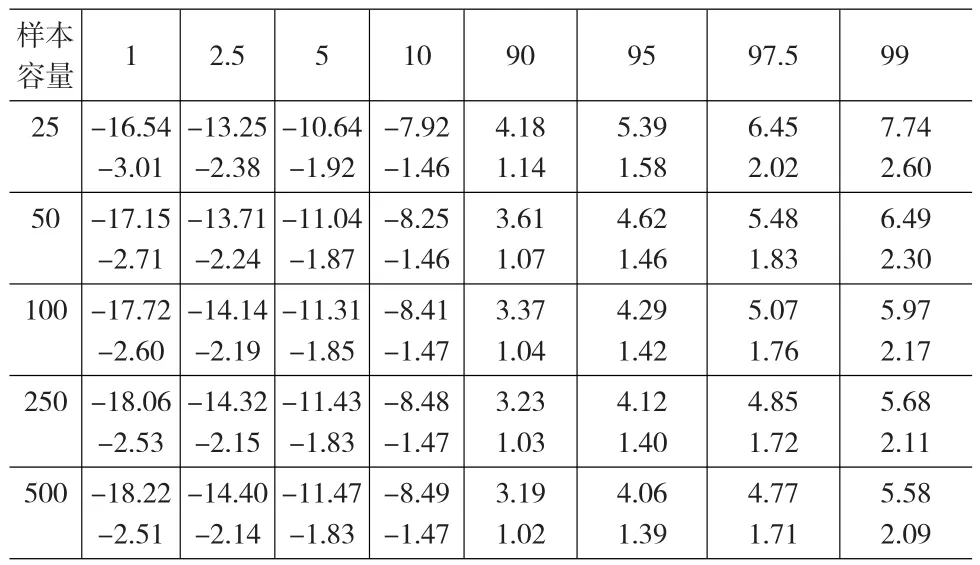
表1 递归趋势调整单位根检验量常见分位数

为比较基于递归趋势调整检验量与经典DF检验量这两类检验方法的优劣，接下来再进行模拟分析，设定模拟次数为10000次，自回归系数 ρ的取值分别为1、0.95、0.90、0.85、0.80和0.75，显著性水平为0.05。表2给出了模拟结果，其中DF1、DF2分别表示对模型（4）采用传统DF检验量对应的系数检验量和伪t检验量，而DFR1、DFR2表示基于递归趋势调整的系数检验量和伪t检验量。

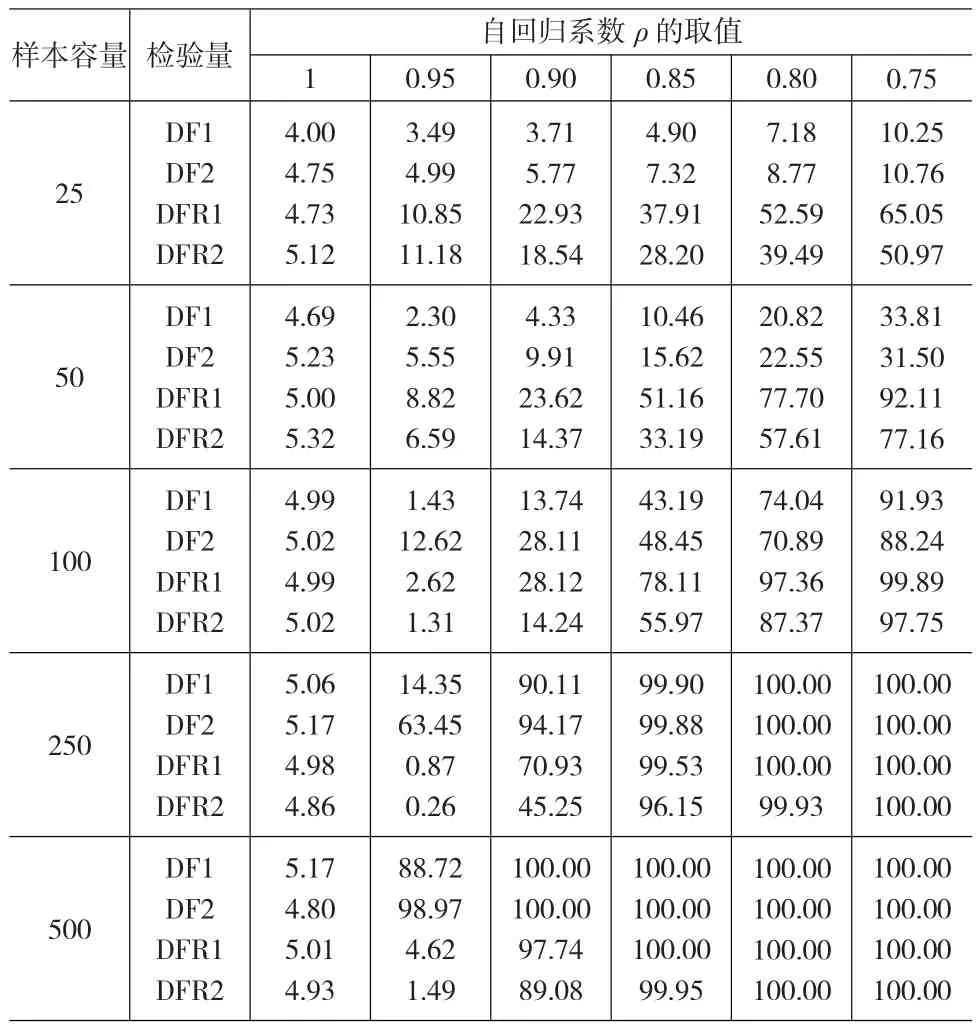
表2 两类检验量的检验水平与检验功效的模拟结果

首先比较两类检验量的检验水平扭曲程度，即当ρ取1时实际拒绝率与名义拒绝率0.05的差异程度。由于模拟的随机性，无论使用哪类检验方法，每类检验的实际显著性水平不可能正好等于名义水平0.05，根据Godfrey和Orme（2000）提供的实际显著性水平区间估计公式，取概率度为1.96得到实际显著性水平的区间估计为（4.57%，5.43%）。根据这个标准，除样本为25且检验量DF1的实际检验水平落在上述区间之外，其它场合的实际检验水平均落在上述区间之内，这表明本文提出的递归趋势调整检验量和经典的DF检验量相比，也具有满意的检验水平。其次就检验功效而言，当样本为25和50时，基于递归趋势调整的两个检验量DFR1和DFR2的检验功效明显高于对应检验量DF1和DF2的结果，且样本越小优势越明显；当样本为100时，DFR1较DF1仍有较高的功效，而DFR2较DF2在 ρ≤0.85时仍有优势；当样本为250和500时，如果ρ≤0.85，则两种检验方法下的检验功效基本相当，但当ρ＞0.85时，传统DF检验量的检验功效明显高于递归趋势调整下对应的检验量结果。这表明，基于递归趋势调整检验量更适合于小样本和中等样本的检验，而当样本较大时，该方法适用于序列偏离单位根过程较远时的检验。

3 结论

对于数据生成为无漂移项的单位根过程而言，本文得到以下几点结论：

（1）采用基于递归趋势调整方法进行单位根检验，当原假设成立时，用于单位根检验的系数检验量和伪t检验量都具有明确的分布，且分布中不含有任何未知的参数，因此可以用于单位根检验，同时也给出了几组样本下检验的分位数，这与文献3和文献4所提出的三种转换方法单位根检验量没有精确分布形成鲜明对比。

（2）蒙特卡罗模拟表明，当原假设成立时，基于递归趋势调整的单位根项估计结果比经典DF检验方法下单位根项估计更为精确，而且系数检验量和伪t检验量都具有满意的检验水平；在检验功效方面，当样本为中小样本时，该检验量在ρ的5种取值中较经典DF检验量都具有更高的功效，而当样本较大时，经典DF检验量具有优势，但此时当序列偏离单位根较远时，两种方法下检验量的检验功效基本相当。因此，当实证分析中的样本较小时，对于此类单位根检验应使用基于递归趋势调整的检验量以降低犯第二类错误的可能。

[1]Bhargava A.On the Theory of Testing for Unit Roots in Observed Time Series[J].Review of Economic Studies,1986,53(3).

[2]Shin D H,So B S,Recursive Mean Adjustment for Unit Root Tests[J].Journal of Time Series Analysis,2001,22(5).

[3]Rodrigues P.Properties of Recursive Trend-Adjusted Unit Root Tests[J].Economics Letters,2006,91(3).

[4]Alanez E L,Alva J A V.Ajuste Recursivo con Transformaciones Invariantes y Bootstrapping:El Caso de Una Caminata Aleatoria Conintercepto[J].EconoQuantum,2010,7(1).

[5]Dickey D A,Fuller W A.Likelihood Ratio Statistics for Autoregressive Time Series With a Unit Root[J].Econometirca,1981,49(4).

[6]Kurtz T G,Protter,P.Weak Limit Theorems for Stochastic Integrals and Stochastic Differential Equations[J].Ann.Probab,1991,(19).

[7]Godfrey L G,Orme C D.Controlling the Significance Levels of Prediction Error Tests for Linear Regression Models[J].Econometrics Journal,2000,3(1).