拖网渔船曳纲的运动建模及仿真

高帅，尹勇，孙霄峰，神和龙

(大连海事大学航海学院，辽宁大连116026)

曳纲作为水下拖缆的一种，其水动力研究可借鉴现有的水下拖缆相关理论成果，根据目前国内外发表的相关文献可知，在拖曳系统的数学模型中应用最为广泛的有两类:有限差分法和集中质量法。Ablow等［1］首次用有限差分法求解拖缆的三维运动，Howell［2］、张潞怡［3］、Sun 等［4］、李英辉［5］、孙霄峰［6-7］对有限差分法进行了进一步修正;Walton等［8］首先采用集中质量法研究了海军武器试验中水下锚链的二维运动响应，Delmer等［9］、Huang［10］、王飞［11］、陈英龙［12］先后对集中质量法进行了改进。国内外学者在进行水下拖缆建模时，大多只考虑模型的精准性及其与模型试验的验证，没有进行可视化和实时性方面的研究。而模拟器中的视景系统为操作者提供一个训练仿真环境，其可视化效果对环境真实感和训练效果具有重要意义。本研究中，在现有拖曳系统水动力理论研究的基础上，忽略曳纲的扭转、抖动、弯矩等，基于集中质量法建模思想，针对拖曳整体运动进行分析，建立拖网渔船曳纲的动态运动模型，并考虑视景显示的实时性要求，利用三维图形引擎OSG(OpenScene-Graph)实现拖曳系统的三维可视化。

1 曳纲稳态运动

当拖网渔船在水中稳定直航时，系统处于相对静止的状态，此时曳纲的运动状态称为曳纲的稳态解。稳态运动方程是一个复杂的非线性偏微分方程组，通过解析解很难得到，只有通过数值方法来近似求解。稳态解是动态运动方程的初始条件。

1.1 坐标系统

为进行曳纲的运动分析计算，采取图1两种坐标系:曳纲惯性坐标系o-ijk和局部坐标系ptnb。在o-ijk中，o为拖点位置，oi、oj轴分别平行于船艏向和船舶右舷正横方向;ok轴垂直水平面向下;在p-tnb中，p为曳纲上一点，pt轴向为曳纲在p点处的切线方向，pn、pb方向分别为在p点处的两个法线方向，pb方向平行于oi、oj所组成的平面。两个坐标系统可以通过拖缆姿态角(θ，φ)相互转换，其中θ为偏航角，φ为俯仰角。它们的转换关系以矩阵形式表示为

其中，

1.2 曳纲稳态运动数学模型

曳纲为细长、柔性的圆柱体，忽略弯矩和扭矩

图1 拖曳系统坐标示意图Fig.1 Schematic diagram of a towed system

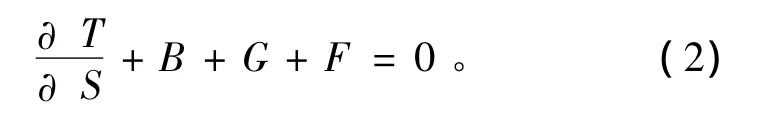
其中:T为微元段曳纲的张力，指向曳纲切向;B、G分别为单位长度曳纲的浮力和重力;F为曳纲受到的流体阻力;S为微元段曳纲拉伸后的弧长。

将式 (2)在曳纲局部坐标系下展开，则平衡方程可写成标量形式［11］:

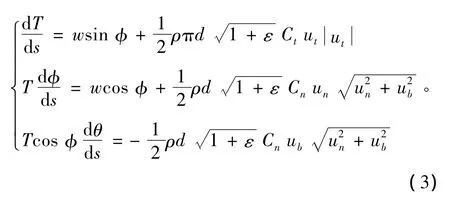
其中:w为曳纲水中质量;ρ为海水密度;d为曳纲截面的直径;s表示未拉伸的曳纲弧长;ε为曳纲的应变;Ct和 Cn为切向和法向阻力系数;ut、un、ub为局部坐标系下的速度分量，由系统相对于水流的拖曳速度转换到局部坐标系下得到，如下式:

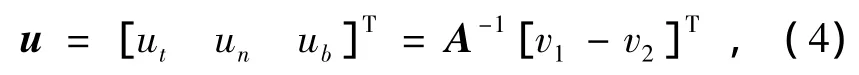
式中，v1为拖曳速度，v2为流速。而曳纲在惯性坐标系下的坐标由下列关系式给出:

给定曳纲在端点处或者任意位置上的状态值(T0，θ0，φ0)，便可由式 (3)通过四阶龙格库塔法进行积分求解，再由式 (5)求出曳纲分段的位置信息。对于两点边值的稳态问题，边界条件不能直接应用到数值求解中，联立方程将转换为关于初始值的隐式方程组，其中初始值(T0，θ0，φ0)为待求量。

1.3 稳态初始值及方程求解

稳态运动控制方程的求解，需要在曳纲首尾两端加上一定的边界条件，将其转变为初始值问题再进行求解。考虑拖船以某一航速匀速直航，在拖曳首端，拖船拖点和曳纲的速度与位置始终一致。此时，ut、un、ub由式 (4)可以直接求出。为验证稳态模型的合理性，先假设均匀海流下拖曳尾端不受渔网的拉力而是自由端，此时，T0=0(T=0对方程 (3)来说为一奇点，可取一接近零的数来代替)和θ0=φ(φ为船艏向)。将T0=0代入式(3)可求得φ0值，如下式所示:

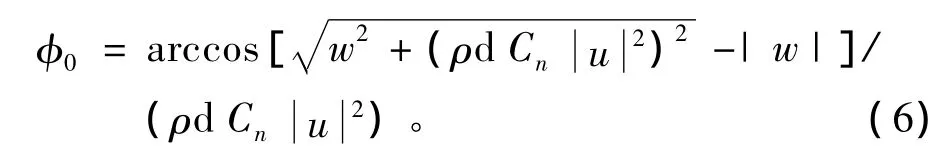
自由端的边界条件表示成一个显式的初始值方程，将(T0，θ0，φ0)代入方程 (3)通过四阶龙格库塔法进行积分求解，而曳纲的首端与拖船相连，拖点的位置 (x0，y0，z0)可认为已知，这样由式(5)求出曳纲分段的位置信息。

为了比较的一致性，考虑均匀流下稳定直航状态，在进行曳纲的分析时采用了文献 ［4］的物理参数，如表1所示。表2为本研究结果与文献［4］的参数对照，可以看出，拖点的俯仰角φ、张力T和曳纲尾端的深度基本一致。曳纲长度不变，尾端为自由端时，仿真计算结果 (图2)表明，随着拖速的增加，拖曳的深度降低;图3表明，随着拖速的增加，拖点张力增大。

表1 曳纲物理参数Tab.1 Physical parameters of the warp

表2 拖曳稳定后相关参数对照Tab.2 Parameter contrast of the trawling stabilization

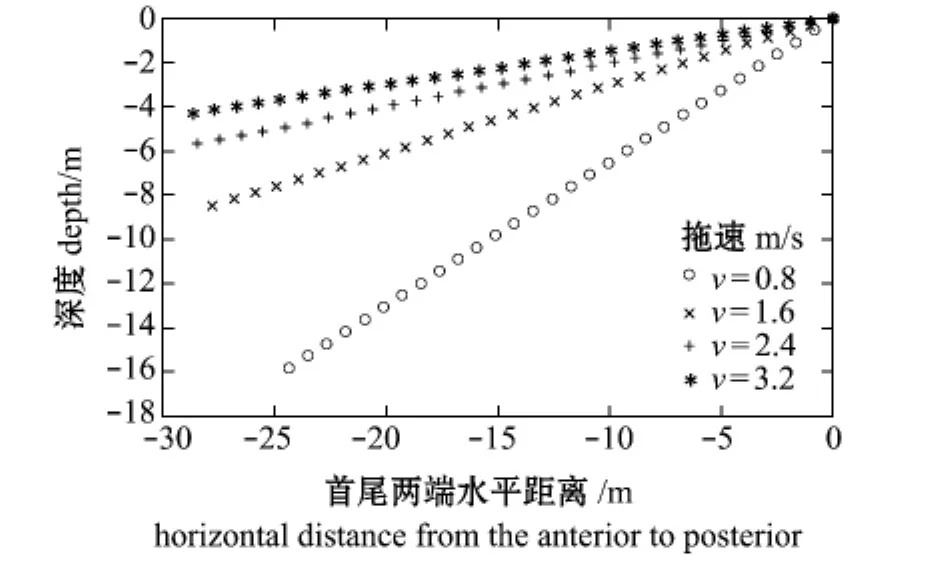
图2 曳纲阵形随拖速的变化Fig.2 Displayed warp at different towing speeds of trawling

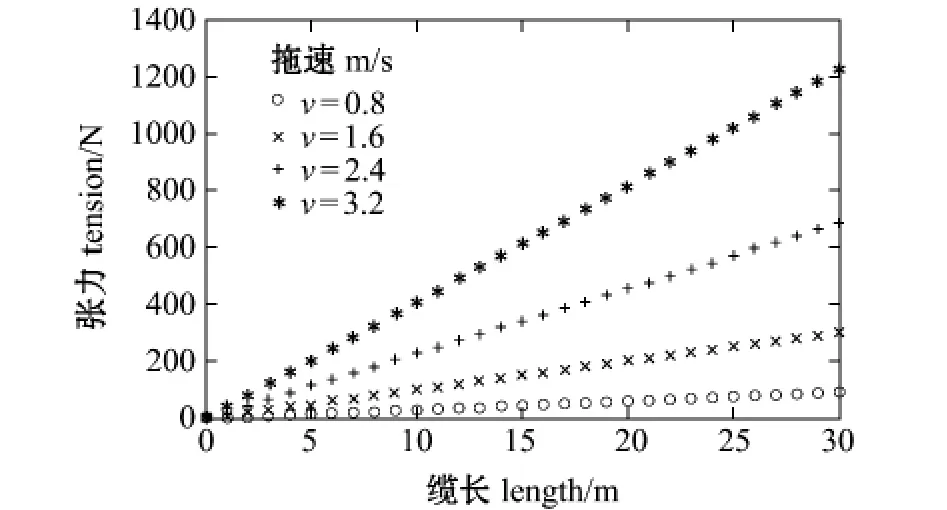
图3 均匀海流不同拖速的张力分布Fig.3 Distribution of strain at different towing speeds in uniform current

2 曳纲动态运动

2.1 曳纲动态运动方程

在曳纲惯性坐标系下对曳纲动态运动进行分析，不考虑弯矩和扭矩的影响，每段的作用力 (重力G、浮力B、流体阻力F和张力T)均集中作用在节点上。对曳纲第i个节点应用牛顿第二定律，建立在流体中运动的曳纲节点i的动力方程:

其中:Mi和Δ Mi分别为节点i的质量和附加质量;为节点i的加速度。

(1)附加质量。流体中的物体加速运动会引起周围流体也做加速运动，流体的质量会引起一个反作用力，相当于物体具有了一个附加质量，即

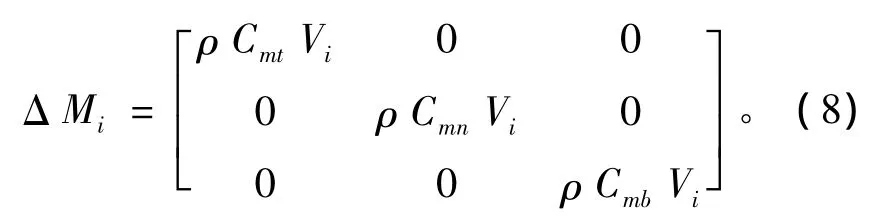
其中:Cmt、Cmn、Cmb分别为局部坐标系各方向的附加质量系数，参考文献 ［12］中的值，Cmt=0，Cmn=Cmb=1．0;Vi表示节点i段的体积。

(2)张力。绳索在拉伸后具有一定的张力。当曳纲尾部为自由端时，尾部节点只受到上一节点的张力作用;当曳纲尾部为拖网时，尾部节点与渔网手纲相连，受到网具的阻力作用。

其中:Tij为曳纲在惯性坐标系受到的张力矢量;E为弹性模量;Aij为i段的横截面积;lij和loij分别为微元段的实际长度和初始长度;e=(lij-loij)/loij。

(3)流体阻力。参照Albow等［1］使用的方法，将拖缆阻力进行简化，分为切向和法向两部分处理:

在曳纲惯性坐标系下，只在垂直方向受到重力和浮力作用，由此，曳纲的动态运动方程 (7)可写成下式:

2.2 边界条件

(1)拖点边界条件。在拖曳的上端点，渔船对曳纲的影响主要是改变了曳纲首节点的位置和速度。设导缆孔在随船坐标系下的坐标为(xw，yw)，转换到空间坐标系下可表示为

其中:Xw、Yw为导缆孔在空间坐标系下的坐标;x、y为渔船重心在空间坐标系下的坐标;φ为船艏向。

导缆孔在随船运动坐标系下的速度可表示为

其中:uw、vw分别为导缆孔处的纵向和横向速度;u、v、r分别为渔船重心处的纵向速度、横向速度和转艏角速度;α=tan-1(yw/xw)。

(2)尾端边界条件。曳纲末端与渔网手纲相连，为简化处理，渔网的阻力采用日本小山武夫网具阻力公式［13］:

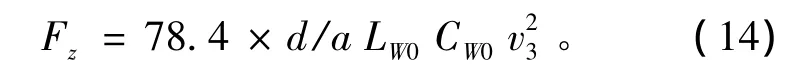
其中:Fz为网具阻力 (N);d/a为网具线面积系数，即网线直径与目脚长度之比;LW0为网具拉直的总长 (m);CW0为网具网口拉直的周长 (m);v3为相对拖速 (m/s)。

将渔网视为一个点融入到曳纲尾部结点i=0的控制方程中，此时边界条件可近似为

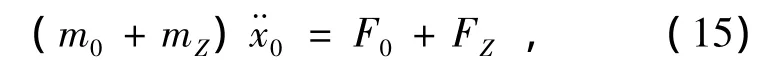
其中，mZ为网具质量。

2.3 曳纲动态方程数值求解

联立控制方程 (7)和相应的边界条件及速度v=dx/dt，便组成一个完整的微分方程组:

采用四阶龙格库塔方法求解此微分方程，便可得到t+Δt时刻的位置和速度，其计算公式如下:

在求解此方程时，张力T是位移的隐式函数，由式 (17)可以看出，单次求解过程需要4次循环后得到节点的位移和速度，在每次循环后更新一次数据，用得到的临时位置来计算各点的张力和流体阻力。用表1的参数进行动态仿真，尾部设为自由端，拖点在30 s内速度从0 m/s加速到 0．8 m/s，此后以0．8 m/s的速度前进，所得到的缆形如图4所示，该缆形与文献 ［4］采用有限差分法所得缆形基本一致。

在实际中，曳纲都是与渔网手纲相连的，而渔网的阻力在不考虑渔获物的情况下受力较大，此时曳纲基本呈直线状态［14］。

对曳纲进行空间离散，离散的段数直接决定了运动方程的复杂程度，即离散段数越多，预测结果精度就越高，但同时计算量就越大。在可视化过程中，既要保证仿真的准确性，又要考虑系统的实时性，从而选择合适的空间步长。图5为本研究中采用集中质量法和文献 ［6］利用有限差分法建立模型的分段数与解算时间的关系，可以看出，集中质量法在实时性方面具有更高的效率。

图4 自由端拖缆阵形的变化Fig.4 Displayed configurations of towed cable with free end

图5 模型分段数与解算时间关系Fig.5 Relationship between solution time and model segments

至此，建立了曳纲的稳态运动模型和动态控制方程，动态运动是以稳态运动作为初始值，进行积分求解得到每个节点的速度和位置，由于采用龙格库塔法求解集中质量模型需满足一定条件才能稳定，即时间步长Δt必须满足一定的稳定性条件，由文献［11］可知，数值稳定性的充要条件为

Eσ/m·Δ t2/Δ s2＜1(σ为横截面积)。

3 拖曳系统的可视化

利用三维图形引擎OSG开发了拖网曳纲的视景驱动程序，根据曳纲的数学模型解算得到各节点的位置信息进行实时绘制，实现曳纲的三维动态可视化，整个系统的仿真流程如图6所示。

图6 仿真流程图Fig.6 Flowing chart of simulation

为增强可视化效果，加入海浪、天空、岛屿等进行渲染，但并不考虑曳纲受到的波浪力。渔船在航行中，船上物体会随渔船发生振荡，这要求曳纲的物理模型要进行相应的矩阵变换。假定渔船的位置矩阵为M，M是一个3×3的矩阵，海面波浪的坐标矩阵为A(posX posY h)，这里(posX，posY)为船所在的海平面坐标，h为该点的波高，则船在波浪里的位置矩阵为M':M'=M·A，船上物体相对船中心的位置为M0(X0Y0Z0)，物体随船振荡的坐标矩阵表示为P=M0·M'。这样便可使得物体随船振荡，如图7所示。

在仿真过程中，将渔网视作水下拖体，不考虑渔网的数学模型。OSG采用一种自上而下的、分层的树状数据结构来组织空间数据集，以提升渲染效率。将渔船、曳纲和渔网分别作为独立的节点，这些节点中包含了几何信息和用于控制其外观的渲染状态信息，通过回调函数进行实时渲染。

将曳纲离散为许多相连的圆柱体，并将纹理对象映射到每个圆柱曲面上，选取纹理对象时首先应注意单个纹理映射到圆柱体上的融合，其次为使相邻两个圆柱体连接时不会出现纹理图像的断裂，纹理图片的上侧与下侧应保证对称［7］。曳纲纹理可视化结果如图8～图10所示。

图7 物体随船振荡Fig.7 Object shaking with ship

图8 曳纲局部可视化效果Fig.8 Local visualization of warp

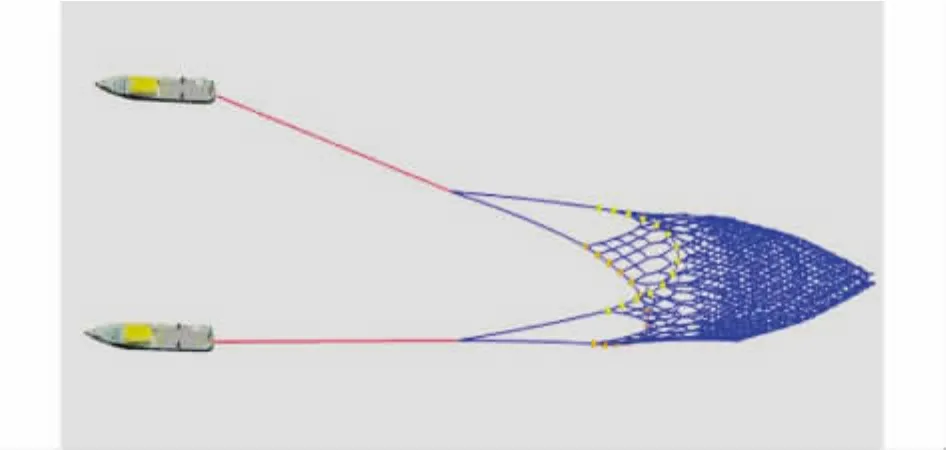
图9 双船拖曳运动 (俯视)Fig.9 Drag motion of a pair trawler(vertical view)

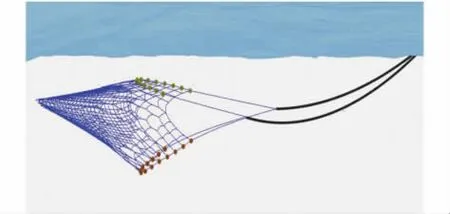
图10 双船拖曳运动 (侧视)Fig.10 Drag motion of a pair trawler(side view)

整个场景的渲染过程中，除去曳纲后系统的渲染帧率基本维持在60帧，这样曳纲模型的解算时间成为影响整个系统实时性的主要因素。分析图5选择合适的空间步长，以满足视景系统实时性的要求。

4 结语

本研究中在现有拖曳系统水动力理论研究的基础上，采用集中质量法建立了曳纲的运动数学模型，最后利用三维图形引擎OSG实现拖曳系统的三维可视化。通过和已有的试验数据对比，证明该数学模型是合理的，在三维可视化中，其显示的速率也得到保证，从而为渔具系统的水动力模型的建立和视景可视化奠定了基础。

［1］Ablow C M，Schechter S．Numerical simulation of undersea cable dynamics［J］．Oceanic Engineering，1983，10(6):443-457．

［2］Howell C T．Investigation of the dynamics of low-tension cables［D］．Massachusetts:Massachusetts Institute of Technology and Woods Hole Oceanographic Institution，1992．

［3］张潞怡．6000米深拖系统非线性运动理论研究及仿真［D］．上海:上海交通大学，1996．

［4］Sun Yang，Lenard J W．Dynamics of ocean cables with local low tension regions［J］．Ocean Engng，1998，25(6):443-463．

［5］李英辉．合成孔径声纳拖曳系统运动的理论与实验研究［D］．哈尔滨:哈尔滨工程大学，2002．

［6］孙霄峰．单船中层拖网系统的建模与仿真［D］．大连:大连海事大学，2008．

［7］孙霄峰，高帅，尹勇，等．渔船模拟器中中层拖网的建模与仿真［J］．大连海洋大学学报，2012，27(3):284-288．

［8］Walton T S，Polachek H．Calculation of transient motion of submerged cables［J］．Mathematics of Computation，1960，14:27-46．

［9］Delmer T N，Stephens T C，Coe J M．Numerical simulation of towed cables［J］．Ocean Engineering，1983，10:119-132．

［10］Huang S．Dynamic analysis of three-dimensional marine cables［J］．Ocean Engineering，1994，21:587-605．

［11］王飞．海洋勘探拖曳系统运动仿真与控制技术［D］．上海:上海交通大学，2006．

［12］陈英龙．拖网捕捞拖曳系统的建模及控制研究［D］．杭州:浙江大学，2013．

［13］崔建章．渔具与渔法学［M］．北京:中国农业出版社，1997．

［14］陈英龙，赵勇刚，周华，等．大型中层拖网网具系统的仿真研究［J］．浙江大学学报:工学版，2014，48(4):625-632．