基于分形盒维数的油膜涡动与油膜振荡轴心轨迹分析

胡道达，马振利，石文凯

(中国人民解放军后勤工程学院研究生管理大队，重庆 401311)

基于分形盒维数的油膜涡动与油膜振荡轴心轨迹分析

胡道达，马振利，石文凯

(中国人民解放军后勤工程学院研究生管理大队，重庆 401311)

在转子实验台上进行实验，模拟滑动轴承正常、共振、油膜涡动、油膜振荡4种工作状态。根据信号的分形特征，对4种状态的50组实验数据进行分形盒维数处理。结果表明:正常运行和共振工作状态的轴心轨迹为椭圆或圆形，其对应的盒维数值分别在1.032 7～1.193 8和1.101 1～1.174 0范围内波动，二者的盒维数值区分度不明显;油膜涡动和油膜振荡轴心轨迹分别为大圆套小圆和不规则紊乱形状，其对应的分形盒维数值分别在1.220 3～1.350 5和1.380 4～1.541 7范围内波动，二者区分度较明显。因此，可以用分形盒维数作为油膜涡动与油膜振荡的故障特征量，通过划分盒维数值区间来准确识别故障状态。

盒维数;油膜涡动;油膜振荡

大功率、高转速机械设备支撑系统通常采用滑动轴承，而油膜涡动与油膜振荡是滑动轴承的常见故障，一旦发生将导致机械系统不能平稳工作。因此，掌握油膜涡动与油膜振荡故障特征对于预防和排除油膜涡动与油膜振荡具有极为重要的意义［1］。目前，油膜涡动与油膜振荡故障特征的主要提取方法是对信号的时、频域进行分析，不能进行准确量化。本文用分形盒维数来定量描述滑动轴承转子系统的轴心轨迹，提出了采用盒维数分析轴心轨迹的油膜涡动与油膜振荡故障特征提取方法。

1 分形及盒维数

目前，学者们对分形没有准确的定义，一般认为在不同尺度下具有自相似的形体是分形体。分形体具有分数的维数，分形维数通常包括:Hausdorff维数、自相似维数、关联维数、盒维数、信息维数、广义维数及Lyapunov维数。由于盒维数计算比较简单，所以本文将盒维数作为故障信号的特征量，以一种简洁的方式定量描述转子系统的状态信息［2］。

盒维数是应用最广泛的维数之一，因为盒维数计算简单，经验估算相对容易。设F是Rn上的任意非空子集，直径(边长)最大为δ的盒子覆盖F集的最少个数为Nδ(F)，则F的上、下盒维数定义为［3］:

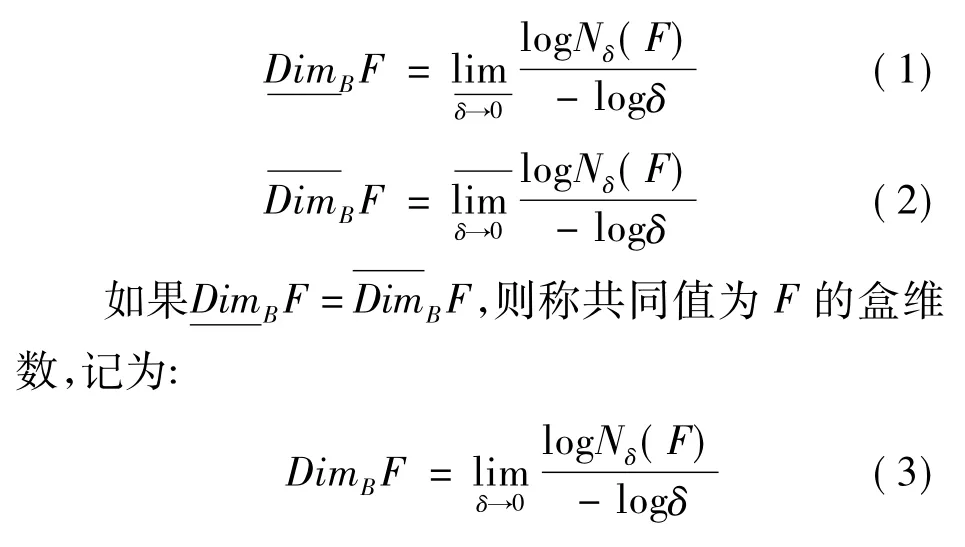
在计算信号盒维数时，一般是构造边长为δ的正方形盒子，然后计算不同δ的值覆盖信号的盒子个数Nδ(F)，通过Nδ(F)-logδ图的斜率值来估计盒维数。盒维数能够度量信号的空间填充能力，一般来说信号越不规则、越复杂、盒维数值越大。信号的盒维数值一般在1～2。因此，可以用盒维数的大小来判别信号的复杂程度［4］。

2 油膜涡动与油膜振荡的常见故障特征

滑动轴承在发生油膜涡动和油膜振荡时，信号的波形、轴心轨迹、频谱图和二维全息谱都会发生很大的变化，这些变化规律可以作为它们的故障特征。油膜涡动和油膜振荡的故障特征有:①油膜涡动时，波形发生畸变;轴心轨迹图呈现大圆套小圆的特征，在频谱图中，油膜涡动在工频约一半处出现峰值;在二维全息谱的涡动频率处会出现偏心率很小的椭圆，且进动方向均为正进动。②油膜振荡时，轴心轨迹图呈紊乱状态;在一阶临界转速处出现峰值［5］。

3 油膜涡动与油膜振荡轴心轨迹实验研究

3.1 实验系统介绍

INV1612型多功能柔性转子实验系统由北京东方振动和噪声技术研究所生产，主要由硬件系统和软件系统两部分组成(图1所示)。硬件系统主要由转子试验台、电涡流位移传感器、光电传感器、电动机、调速器、数据采集仪和计算机组成。INV1612型多功能柔性转子实验配有 DASPINV1612软件。该软件可以实现波形分析、频谱分析、波谱分析、x-y轴心轨迹分析、谱阵分析、幅值分析等功能。本文利用了该实验系统模拟滑动轴承油膜涡动与油膜振荡的故障特征规律。

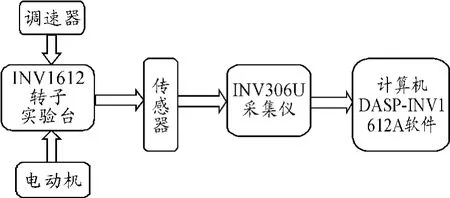
图1 INV1612型多功能柔性转子实验系统

3.2 测试原理与参数设置

本实验测试原理如图2所示。实验数据文件有3个通道，其中1#通道与光电速传感器连接，测量转轴速度;2#通道和3#通道与位移传感器连接，其中2#通道测量x方向的振动信号，3#通道测量y方向振动信号。轴心轨迹图由x-y方向合成，振幅转速图与2#通道连接。本实验设置采样频率为2 048 Hz，采样点数为1 024，滤波方式为0-1x低通滤波(保留基频及以下的频率段)，位移传感器灵敏度为8.0 V/mm，工程单位为μm。电机转速控制在8 000 r/min内。

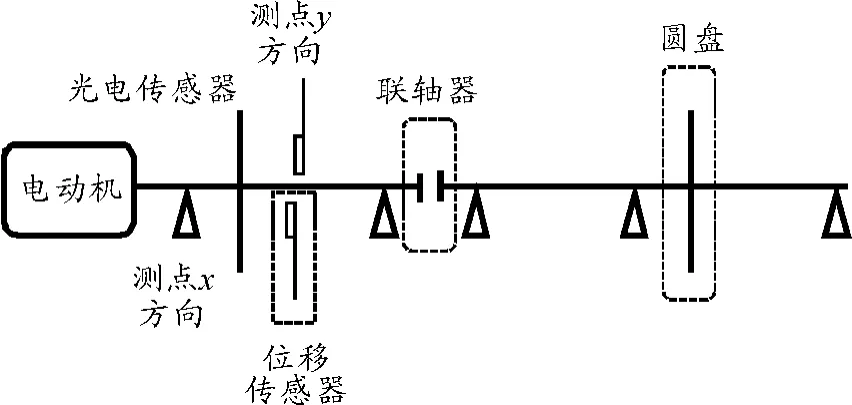
图2 测试示意图

3.3 数据分析

通过调速器将电机转速逐步提高到8 000 r/min时，基频振幅-转速曲线如图3所示。从图中可以看出:在大约2 700～3 000 r/min时，幅值明显增大;在2 900 r/min时出现峰值，大约为800 μm。由此可以判断转轴的临界转速大约在2 700～3 000 r/min。在实验操作时，为了避免共振给实验装置带来损坏，应尽快通过临界转速区。半频振幅-转速曲线如图4所示。从图中可以看出:在约3 800 r/min时出现半频成分，油膜涡动发生;在5 600 r/min时出现峰值，油膜振荡发生;此时转速大约为临界转速的2倍。因此，转轴在不同转速下共有4种工作状态，即正常运行状态、共振状态、油膜涡动状态与油膜振荡状态。4种状态的波形与轴心轨迹分别如图5～8所示。将实验测得的50组4种状态轴心轨迹数据用Fractal-Box2.0软件进行盒维数计算，计算结果如表1所示。

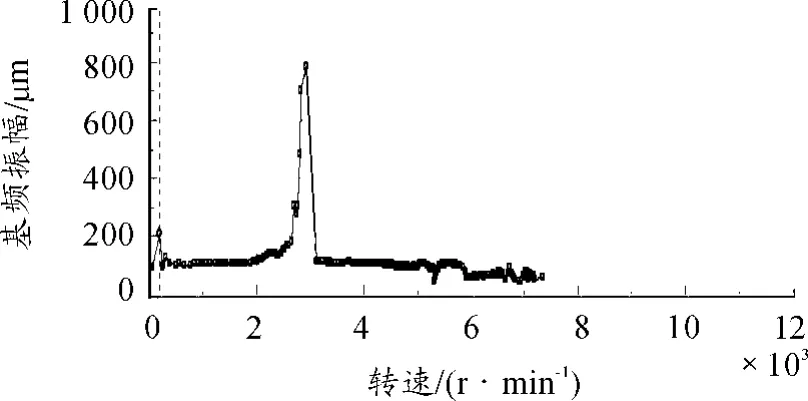
图3 基频振幅-转速曲线

图4 半频振幅-转速曲线

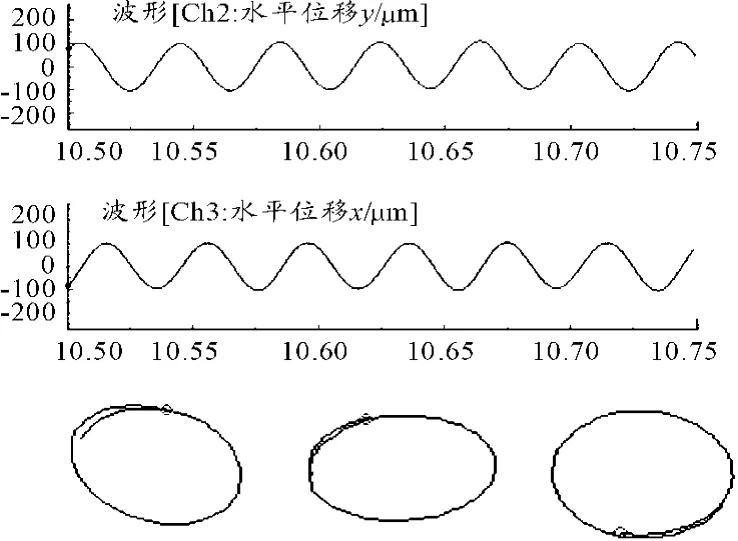
图5 正常状态的波形和轴心轨迹

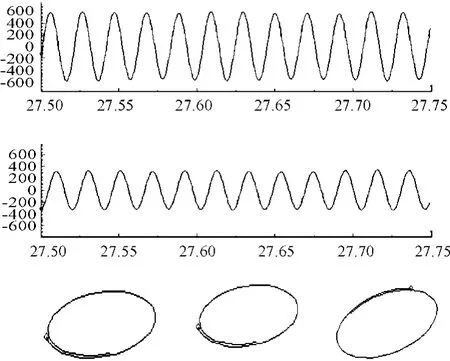
图6 共振状态的波形和轴心轨迹

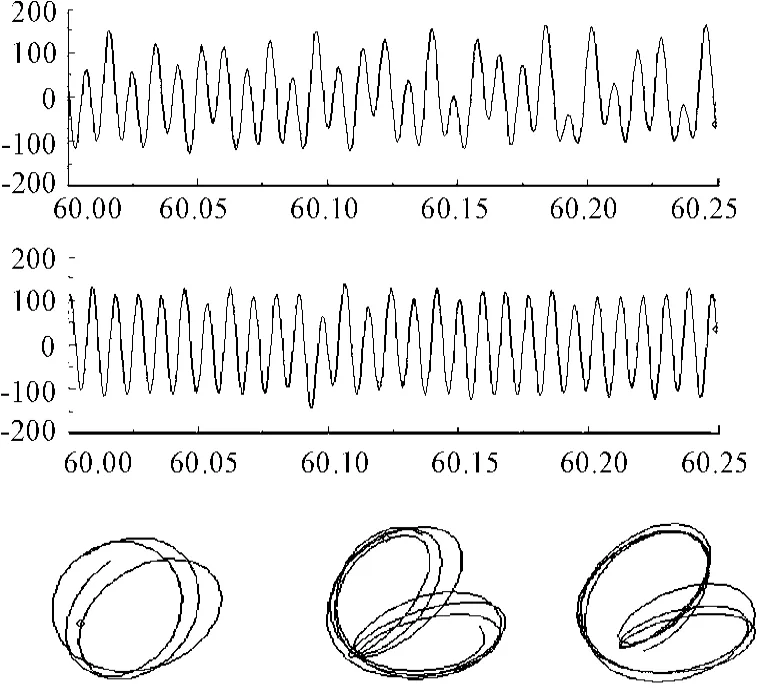
图7 油膜涡动状态的波形和轴心轨迹

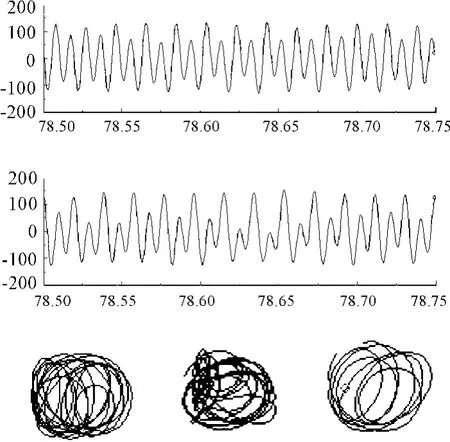
图8 油膜振荡状态的波形和轴心轨迹

表1 转子在不同状态下轴心轨迹分形盒维数

从表1和转轴在不同状态下的轴心轨迹图可以看出:转轴在不同状态下有不同的盒维数，其中正常状态轴心轨迹为椭圆或近似圆形，盒维数均值最小，为1.087 5;临界转速状态轴心轨迹图为椭圆形，盒维数均值为1.148 1;油膜涡动轴心轨迹类似大圆套小圆的形状，盒维数均值较大，为1.299 7;油膜振荡轴心轨迹图为不规则散乱形状，盒维数均值最大，为1.460 6。从而可以看出:转子系统在不同状态下的盒维数具有较好的区分度，但在正常状态和临界转速状态下，盒维数值相差较小，区分度不明显，正常状态的盒维数值在1.032 7～1.193 8，临界转速状态盒维数值在1.101 1～1.174 0，2种状态的盒维数值可能出现重合的情况;油膜涡动状态、油膜振荡状态两者之间盒维数值区分度较大，油膜涡动的盒维数值在1.220 3～1.350 5，油膜振荡的盒维数值在1.380 4～1.541 7，油膜涡动的最小值与正常状态的最大值相差0.026 5，油膜振荡的最小值与油膜涡动的最大值相差0.029 9，没有出现重合情况。因此，盒维数可以作为转子系统油膜涡动与油膜振荡的故障特征量，定量实现转子系统油膜涡动与油膜振荡的诊断，但不能作为临界转速的故障特征量。

产生这种现象的原因是:盒维数能够度量信号的空间填充能力，在正常状态和临界状态下，成周期的正弦曲线，轴心轨迹图为规则的椭圆或圆形，两者信号空间填充能力相差不大，所以盒维数值小且区分度不明显;在油膜涡动和油膜振荡发生时出现半频成分，信号发生畸变，油膜涡动轴心轨迹图为大圆套小圆的形状，油膜振荡轴心轨迹图为散乱不规则形状，所以油膜涡动与油膜振荡轴心轨迹的盒维数值较大，区分度较明显。

3.4 划分状态区间

盒维数可以作为油膜涡动与油膜振荡的故障特征量。但在实际的的转子系统中，油膜涡动与油膜振荡的盒维数值不是恒定不变的，而是在各自的维数值区间内波动。因此，要用盒维数值实现油膜涡动与油膜振荡的判别，需要对各自的状态划分区间。如果油膜涡动的盒维数值区间在［a1，a2］之间，只要转子系统轴心轨迹的维数值在区间［a1，a2］内，则认为转子系统发生了油膜涡动，油膜振荡判别同理［6］。

从表1可知:转子系统正常状态最大盒维数值为1.193 8，油膜涡动的维数值在1.220 3～1.350 5，油膜振荡的维数值在1.380 4～1.541 7。在划分状态区间时，以某一状态的最大值和最小值作该状态区间的2个端点，油膜涡动的最小值为1. 220 3，最大值为1.350 5，由于该值只是对50组实验数据进行统计分析，在实际的油膜涡动判别中可能会出现维数值比1.220 3小或比1.350 5大的情况，所以为了更准确地实现油膜涡动的判别，可以适当放宽维数值区间。由于油膜涡动的最小值与正常状态的最大值相差0.026 5，二者状态各取一半。油膜涡动盒维数的最小值可在此基础上减小0.026 5/2(取3位有效数值);油膜涡动的最大值与油膜振荡的最小值相差0.029 9;油膜涡动盒维数的最大值可以放宽到1.350 5+(0.029 9/2);油膜振荡的最小值可放宽到1.380 4-(0.029 9/2);油膜振荡的最大值右边无状态区间，可以无穷放宽。根据盒维数定义和在实际的油膜振荡识别中，轴心轨迹维数值绝不可能超过2，以1.999 9作为油膜振荡状态区间的最大值。因此，油膜涡动与油膜振荡的状态区间划分结果如表2所示。

表2 转子系统状态区间

4 结论

1)根据实验数据显示:滑动轴承转子系统由低速到高速的工作过程中，会经历临界转速、油膜涡动、油膜振荡3个运行状态。在临界转速状态，基频振幅出现峰值;在油膜涡动状态，信号发生畸变，出现半频成分，且半频振幅较小，轴心轨迹出现大圆套小圆的形状;在临界转速2倍左右时，出现油膜振荡状态，半频振幅出现峰值，轴心轨迹为紊乱状态。

2)在正常运行和临界转速状态，轴心轨迹分形盒维数较小，均值分别为1.087 5和1.148 1，二者区分度不大，在2种状态下可能会出现维数值重合;在油膜涡动、油膜振荡运行状态轴心轨迹分形盒维数较大，均值分别为1.220 3和1.380 4，二者区分度较大，在2种状态下，不会出现维数值重合。因此，可以用轴心轨迹的盒维数作为油膜涡动和油膜振荡的故障特征量。

3)油膜涡动状态盒维数值区间为［1.207 3，1.365 4］，油膜振荡的维数值区间为［1.365 5，1.999 9］。因此，可以通过维数值区间来判别油膜涡动和油膜振荡状态。

［1］朱瑜，张朋波，王雪.转子系统油膜涡动及油膜振荡故障特征分析［J］.汽轮机技术，2012(4):306-308.

［2］Falconer K.Fractal geometry:mathematical foundations and applications［M］.Chichester:John Wiley & Sons，2004.

［3］张济忠.分形［M］.北京:清华大学出版社，2011.

［4］刘晓波，马善洪.基于分形盒维数的裂纹转子故障诊断［J］.仪器仪表学报，2008，29(4):497-499.

［5］张新勇，段滋华.滑动轴承油膜涡动和油膜振荡故障诊断及在线消除［J］.煤矿机械，2008(1):196-199.

［6］郝研.分形维数特性分析及故障诊断分形方法研究［D］.天津:天津大学，2012.

(责任编辑陈 艳)

Axis Track Analysis on Oil Whirl and Oil Oscillation Based on Fractal Box Counting Dimension

HU Dao-da，MA Zhen-li，SHI Wen-kai
(The Production Brigade of Graduate Student Management，Logistics Engineering University of PLA，Chongqing 401311，China)

The paper simulated four working conditions of sliding bearing in the rotor platform，which includes regular work condition，resonance condition，oil whirl condition and oil oscillation condition. According to the fractal characteristics of vibration signal，the fractal box counting dimension of experimental data so groups about four working conditions was calculated.The results show that the axis track under regular working and resonance condition is ellipse or roundness，and the fractal box counting dimensions of which vary from 1.032 7 to 1.193 8 and 1.101 1 to 1.174 0，so their results are not distinguished and that the axis track under oil whirl condition and oil oscillation condition are greatcircle of small round and irregular shape，and the fractal box counting dimensions of which vary from 1.220 3 to 1.350 5 and 1.380 4 to 1.541 7，so their results can be distinguished easily.So the fractal box counting dimension can be used as fault characteristic quantity of oil whirl condition and oil oscillation and they can be distinguished by dividing box counting dimension interval.

box counting dimension;oil whirl;oil oscillation

TH13

A

1674-8425(2015)11-0078-05

10.3969/j.issn.1674-8425(z).2015.11.013

2015-06-11

中国人民解放军总后勤部基金(YX214J038)

胡道达(1987—)，男，四川德阳人，硕士研究生，主要从事石油与天然气工程研究。

胡道达，马振利，石文凯.基于分形盒维数的油膜涡动与油膜振荡轴心轨迹分析［J］.重庆理工大学学报:自然科学版，2015(11):78-82.

format:HU Dao-da，MA Zhen-li，SHI Wen-kai.Axis Track Analysis on Oil Whirl and Oil Oscillation Based on Fractal Box Counting Dimension［J］.Journal of Chongqing University of Technology:Natural Science，2015 (11):78-82.