凹槽凸轮的快速建模与变步长数控加工

吴新良

(厦门理工学院现代工程训练中心，厦门 361024)

凹槽凸轮的快速建模与变步长数控加工

吴新良

(厦门理工学院现代工程训练中心，厦门 361024)

基于解析法设计了盘形凹槽凸轮，并用Matlab进行相关计算输出凸轮轮廓点，给出了具体编程实现。将凸轮轮廓点作为CAD样条曲线的控制点进行凸轮轮廓线的快速建模，建模过程直观且容易实现。最后采用变步长直线插补凸轮非圆轮廓线进行数控加工，提高了加工效率。该方法为盘形凸轮的建模和数控加工提供了参考。

凹槽凸轮;建模;数控加工;刀具路径

凸轮机构可实现各种复杂的运动要求，且结构紧凑，因而广泛应用于各种自动机械、仪器和操纵控制装置。在凸轮机构中又以盘形凸轮应用较多，因此相关建模和数控加工得到了广泛的重视［1-4］。本文利用Matlab强大的计算能力，结合CAD绘制样条曲线的便利性，快速进行凸轮的数字化建模，并利用变步长直线快速插补对凸轮非圆轮廓进行加工。该方案在满足精度要求的情况下具有程序段少、加工效率高、容易实现等特点。

1 基于解析法的凹形凸轮的快速CAD建模

根据凹槽凸轮解析法设计，其中心线理论表达式为［5-6］

带滚子的凸轮内、外轮廓曲线为

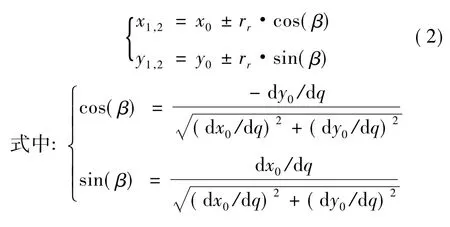
其中:为凸轮转角，凸轮顺时针转动取正值，逆时针转动取负值;s为推杆位移方程，为转角q的函数表达;r0为凸轮基圆半径;e为偏向距，若凸轮从动件导路偏在y轴的右侧则取正值，若偏在在y轴左侧则取负值，若对心则取0;rr为从动件滚子半径。

由上述公式可知:要进行凹槽凸轮的解析设计，必须要计算相关导数等信息。Matlab具有强大的数学运算功能，在工程计算中得到了广泛的应用。现以应用在某重力驱动的避障小车中的凹槽凸轮［7］为例进行CAD快速建模，其推杆位移方程为:

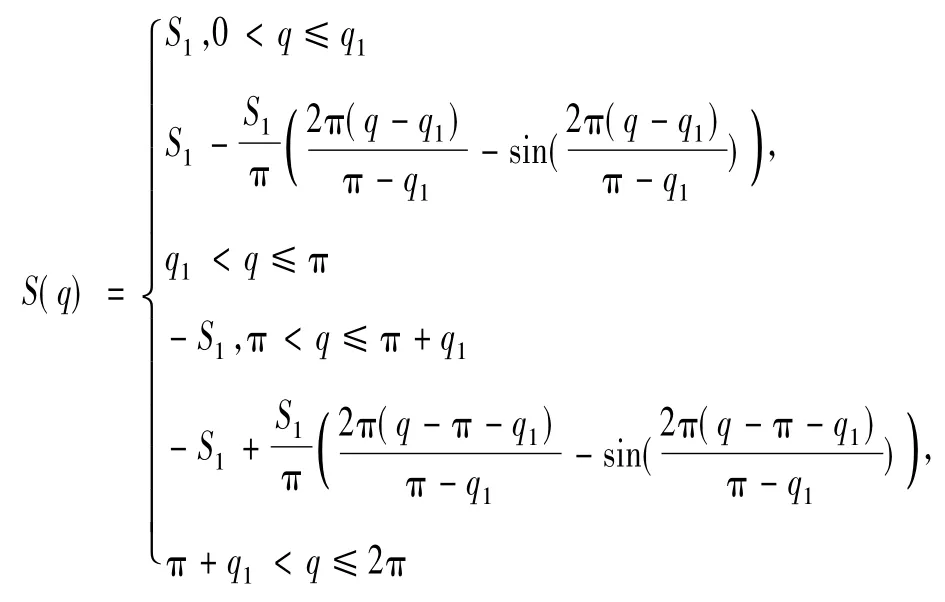
式中:q1=1.55 rad;S1=12.19 mm。

相关Matlab代码如下:

运行该Matlab程序即可在硬盘上得到凸轮理论轮廓点数据文件“cam_center.txt”。限于篇幅，上述程序末尾省略凸轮内、外轮廓点数据的写入程序段，只需将程序末尾的数组x0、y0改成相应的x1、y1和x2、y2即可得到凸轮内、外轮廓点数据文件。应当指出的是，该Matlab程序有较强的通用性，对不同的平面凸轮，只需将其中的推杆位移表达稍作修改即可满足使用要求。

利用平面CAD软件，运行“样条曲线“命令，并将上面得到的各凸轮轮廓数据点复制并粘贴到CAD程序命令框中作为样条曲线的控制点，最后将样曲线条闭合并指定切向即可得到凸轮各轮廓曲线的CAD格式图形，如图1所示。

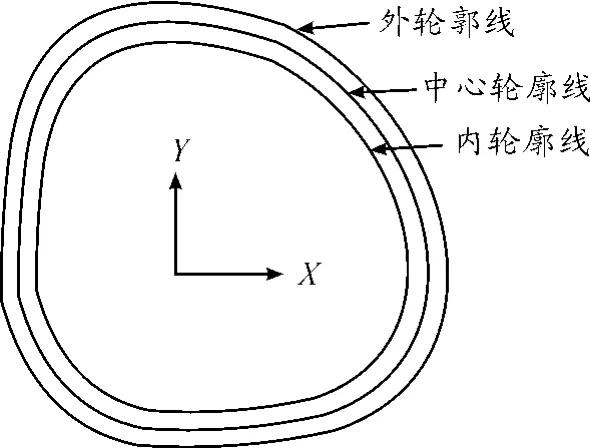
图1 CAD样条曲线绘制凹形凸轮轮廓

在三维造型软件Pro/E中进入“草绘“命令，从其中“文件系统”导入图1中CAD绘制好的凸轮轮廓图文件，即可进行凸轮的三维拉伸建模。凹形凸轮轮廓的三维建模如图2所示。

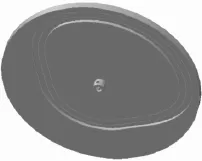
图2 凹形凸轮轮廓的三维建模

上述建模方法充分利用了Matlab较强的计算功能和二维CAD软件的易用性，相比一些文献直接利用三维软件通过参数法建模的方法更直观、更容易实现。

2 凹形凸轮变步长数控加工

凹形凸轮轮廓曲线由2段圆弧和连接圆弧的非圆曲线组成。因大多数控机床提供直线和圆弧插补功能，故须用直线或圆弧拟合非圆曲线。其中圆弧样条利用多段相切圆弧插补非圆曲线［8］，使得加工表面比较光滑，但计算过程复杂费时，较适用于精密加工场合。在直线拟合时利用多段微小直线逼近非圆曲线，因线段连接没有切向连续，不如圆弧拟合光滑，但计算相对简单，速度较快，适用一般应用。该方法是大多数商用CAM软件加工非圆曲线生成刀具路径的常用方法。直线插补非圆曲线的核心在于能在满足精度要求的情况下尽可能增大加工步长以提高加工效率。确定加工步长的方法主要有等参数法、等步长法和等弓高误差法［9-11］。等参数法和等步长法均取误差最极端的情况考虑加工步长增量，导致加工步长最为保守，加工效率较慢。

本文采用等弓高误差法对凸轮轮廓刀具中心线进行直线插补。定义相关弓高误差如图3所示。凸轮轨迹在微小段内其曲率半径单调变化，凸轮轨迹与插补的微小线段最大实际误差εmax在插补直线段的中间点附近，实际求解较为困难。如图3所示，在凸轮轮廓微小段内，过凸轮轨迹上两点且以ρi为半径的圆弧代替实际轮廓线，相应圆割线中点的弓高误差为δ，则有εmax≤δ。若以δ作为加工允许误差代替实际误差εmax，则依此插补的直线段必需符合加工精度要求，且该微小直线段随着曲率半径ρi的变化步长是不断变动的，避免了等参数法和等步长法中步长取固定值导致加工效率不高的情况。

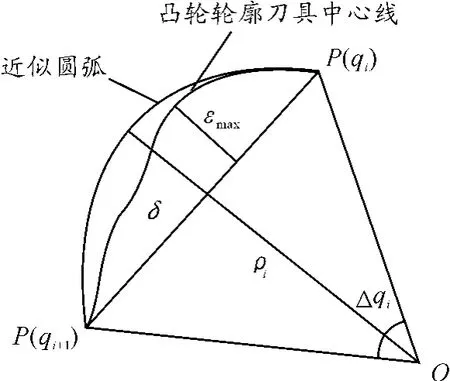
图3 凸轮曲线微小直线逼近

当前点为p(qi)，现求下一点p(qi+1)，即求Δqi。由图3可知:

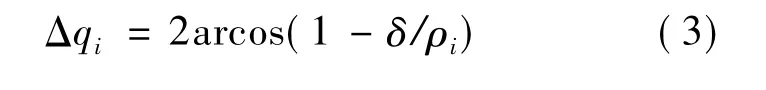
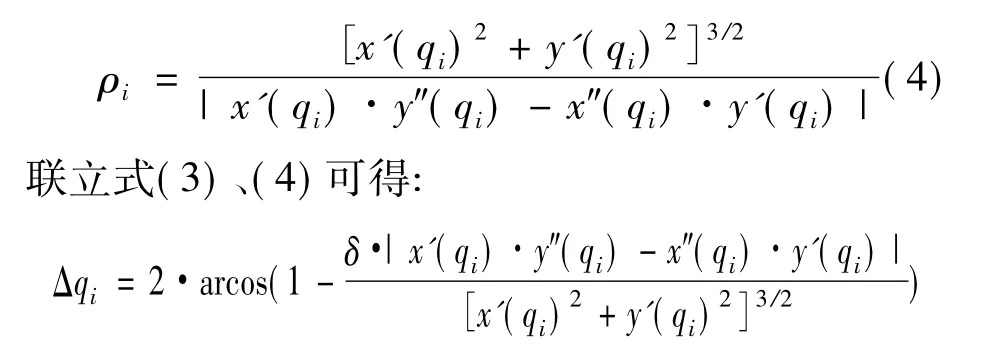
凸轮曲线点p(qi)曲率半径为

变步长凸轮轮廓数控编程算法流程如图4所示，其中x(q)，y(q)为凸轮轮廓刀具中心线方程。若刀具直径等于凸轮滚子直径，则该方程为式(1);否则将式(2)中rr替换为偏置距离，大小为凸轮滚子直径差与刀具直径差，且相应地往外偏置取“+”，往内偏置取“-”。算法流程中Δq选取也如上所述。

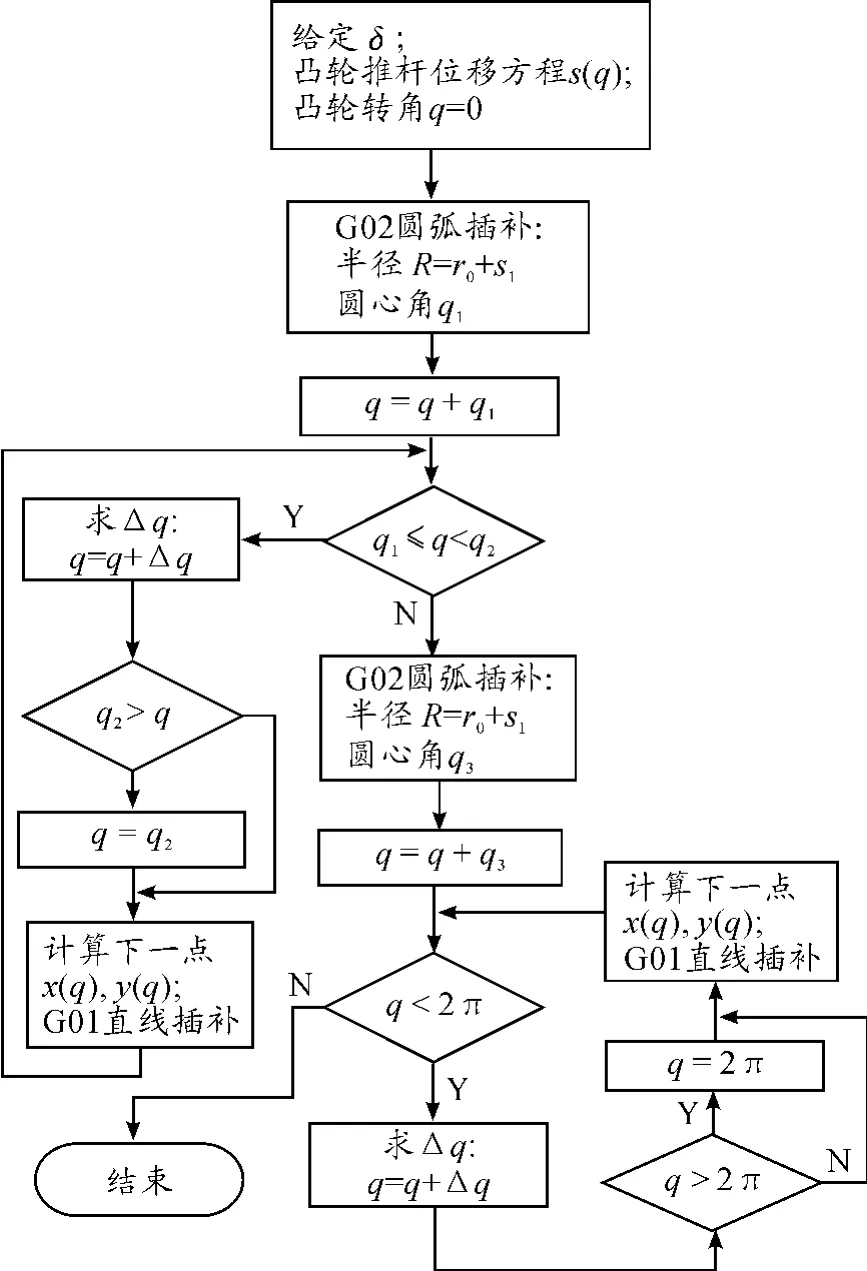
图4 变步长凸轮轮廓数控编程算法流程

该算法对凸轮远休止角q1对应的轮廓段作圆弧插补;接着对凸轮回程角(q2-q1)所对应的非圆轮廓段进行变步长直线插补;然后对凸轮近休止角(q3-q2)所对应的轮廓段进行圆弧插补;最后对凸轮的推程角(2π-q3)所对应的非圆轮廓段进行变步长直线插补。这样保证了误差在要求范围内，且插补步长依凸轮曲率半径变化而变化，从而提高了加工效率。以本文的凸轮为例，采用直径10 mm铣刀，取弓高误差δ为0.01 mm，遵循图4算法，利用Matlab辅助计算生成数控加工代码，其非圆曲线直线插补的步长情况如图5所示。图5中每段非圆段直线插补数为66条，最大步长ΔL=3.21 mm，平均步长为1.40 mm。

在相同弓高误差下，若采用等参数法，在凸轮最大曲率半径为37 678.77 mm处的步长转角增量最小，即Δq=0.001 5。以此等参数增量对每段非圆段进行直线插补，则插补线段数须为1 093条，显然图4算法变步长加工步数明显较少。若用等步长法，非圆曲线的直线插补允许的最大步在最小曲率半径为ρmin=34.46 mm处，ΔL为0.83 mm，显然小于图5的平均步长，即加工效率低于变步长法。

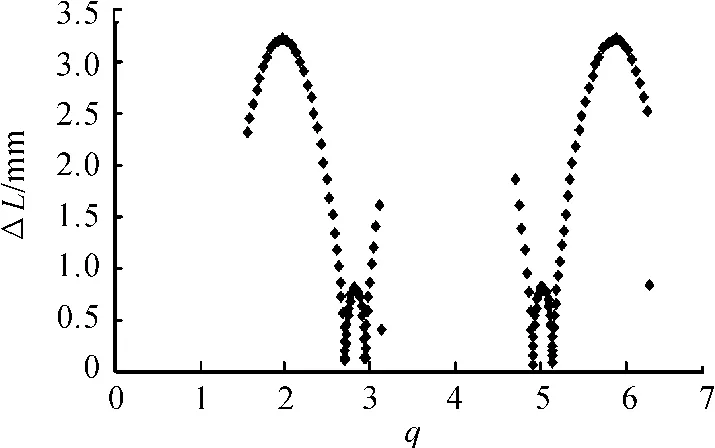
图5 凸轮非圆曲线变步长直线插补步长

将算法生成的数控代码输入机床进行实际加工，得到的凸轮轮廓表面质量良好，与凸轮滚子滚动配合顺利。加工结果如图6所示。

图6 示例凸轮变步长加工实物

3 结束语

采用解析法并用Matlab计算得到凹形凸轮各轮廓线轨迹点，将其输入作为CAD样条曲线控制点进行凸轮轮廓线的快速建模，方法较直观简便。建模后采用直线变步长插补凸轮非圆曲线，加工效率较高。

［1］路宗新.基于数控铣床的平面凸轮铣削加工方法研究［J］.煤矿机械，2010(1):123-125.

［2］杨德卿，姜小兰.平面凸轮极坐标数控加工研究［J］.机械传动，2010(8):83-86.

［3］林鹏，夏重，张晓洪，等.基于Pro/NC的高速凸轮数控加工的实现［J］.机床与液压，2012，40(17):130-133.

［4］谭哲丽，李克天，郑德涛.参数化转换凸轮轮廓及自动生成NC代码［J］.机床与液压，2001(6):29-31.

［5］陈静，杨安杰，李春明.凹槽凸轮轮廓线的解析设计及C语言实现木［J］.组合机床与自动化加工技术，2011 (5):105-107.

［6］丁丙坤，夏田，陈少博.平面凸轮铣削宏指令的开发［J］.河南科技大学学报:自然科学版，2014(4):10-12，17.

［7］吴新良，刘建春，郑朝阳.重力驱动的避障小车设计与制造［J］.机械设计，2014(10):25-28.

［8］陈明君，赵清亮，董申，等.基于双圆弧步长伸缩数控插补非圆曲线算法的研究［J］.机械工程学报，2003，39(1):110-116.

［9］Elber G C E.Tool path generation for freeform surface models［J］.Comput Aided Design，1994，26(6):490 -496.

［10］刘雄伟.数控加工理论与编程技术［M］.2版.北京:机械工业出版社，2001.

［11］赵世田，赵东标，付莹莹.自由曲面加工刀具路径生成高精度变步长算法研究［J］.机械科学与技术，2010 (1):32-35.

(责任编辑刘 舸)

Fast Modeling and Variable Step Size Tootpath CNC Manufacturing of Concave Cam

WU Xin-liang
(Mordern Engineering Training Center，Xiamen University of Technology，Xiamen 361024，China)

The groove cam was designed based on the analytical method，and the detail MATLAB programe was introduced and used to calculate and output cam sharp points，thus the programming realization was given.The sharp curve of cam was built up rapidly by treating CAM contour point as the control point of CAD，and the modeling method is intuitive and easy to implement.Then the variable step size linear was used to have the interpolation cam contour line for computer numeric control machine manufacturing cam，and machining efficiency is improved by using this method.This paper provides a reference for modeling and CNC machining of cam.

concave cam;modeling;computer numerical control machining;toolpath

TH164

A

1674-8425(2015)11-0073-05

10.3969/j.issn.1674-8425(z).2015.11.012

2015-09-09

福建省教育厅科技项目(JB13158)

吴新良(1981—)，男，福建仙游人，硕士，实验师，主要从事数字化设计与制造研究。

吴新良.凹槽凸轮的快速建模与变步长数控加工［J］.重庆理工大学学报:自然科学版，2015(11):73-77.

format:WU Xin-liang.Fast Modeling and Variable Step Size Tootpath CNC Manufacturing of Concave Cam［J］. Journal of Chongqing University of Technology:Natural Science，2015(11):73-77.