近距离开挖卸荷条件下运营地铁高架桥墩响应研究

张子新 ，李佳宇 ，周 湘 ，李文勇

（1.同济大学 地下建筑与工程系，上海 200092；2.同济大学 岩土及地下工程教育部重点试验室，上海 200092；3.上海轨道交通有限公司，上海 200092）

1 引 言

从20 世纪90年代初至今，上海轨道交通全网运营线路总长已超过560 km，车站共计300 余座。绝大部分地铁车站都建设在中心城区，周围环境复杂，而且基坑施工场地狭小、条件复杂[1]，建设难度非常高。基坑的开挖实际上是一个水平和竖向压力同时卸载的过程[2]，卸载导致基坑周围地层变形，对周围建筑、设施产生影响甚至致其破坏，施工时如处理不当，可能酿成重大事故，引起严重城市地质灾害，从而导致经济财产和人民生命的损失[1,3]。开挖卸载引起地层移动会对邻近建构筑物的桩基础产生附加挠度和弯矩，如位移过大则会进一步导致建构筑物的破坏[4]。

目前，绝大多数临近桩基础的基坑为单面相邻，丁勇春[5]，王成华等[6]均对此进行了研究，并在结构内力、位移、桩承载力变化等方面取得了很多有益的结果。本研究面对的工程背景是在运营地铁高架下方进行深基坑施工，并且有一根高架桥墩位于基坑中部，其周围的土体要全部开挖，这样的全周卸荷对高架桥墩的影响如何，国内外鲜有相关的先例及经验。

本文将以上海地铁12 号线龙漕路车站基坑工程为依托，利用FLAC3D有限差分软件建立精细的三维计算模型，对近距离卸荷引起的运营地铁高架桥墩及其基础的响应展开详细研究。

2 工程背景

上海12 号线龙漕路站位于龙漕路、近龙吴路交叉口，车站主体呈东西向布置，与运营3 号线龙漕路站换乘，车站基坑位置平面图如图1 所示。车站主体为地下二层结构，基坑开挖深度为16.5～19.1 m，外包长度为158 m，标准段外包宽度为19.4 m。车站附属结构位于主体结构的两侧，附属结构均为地下一层结构，基坑开挖深度为9.5 m 左右，基坑外包长度为160 m，最大宽度为30 m。主体基坑采用地下连续墙围护，深度为38 m，宽为0.8 m；附属基坑采用φ 1 000 mm 钻孔桩灌注围护，深度为23 m。基坑坑底相关区域采用旋喷桩加固。

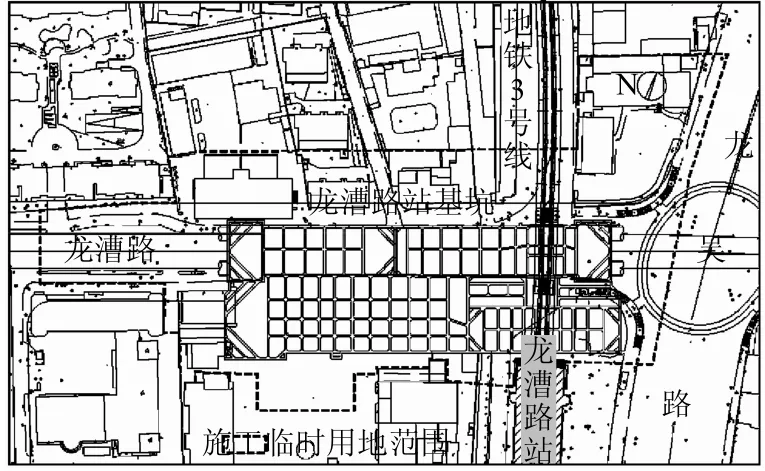
图1 基坑位置平面图Fig.1 Plan of excavation site

工程场址位于城市中心区域，车站主体及南侧附属结构均下穿3 号线高架，高架下方净空只有5 m。3 号线高架共有3 根桥墩紧邻基坑，基坑围护结构距北侧桥墩（A 桥墩）承台约1.3 m，距南侧桥墩（C 桥墩）约1.2 m；中间的桥墩（B 桥墩）位于车站基坑内部，其周围的土体要全部开挖。其中对卸载最严重的B 桥墩采用了MJS 工艺进行了全周加固。基坑施工时，除需保证自身安全外，还必须确保3 号线的正常运营，因此，本工程的建设难度非常高。

工程拟建场地位于古河道地层沉积区。在所揭露深度80.55 m 范围内均属第四系河口、滨海、浅海、沼泽、溺谷相沉积层，场地土层自地表从上至下依次为：填土、粉质黏土、淤泥质粉质黏土、淤泥质黏土、黏土、砂质粉土及粉砂。

场地地下水属第四纪孔隙潜水，补给来源主要为大气降水与地表径流，其水位动态变化主要受大气降水和地表径流影响。地下水埋深一般为0.90～2.40 m，上海地区地下水年平均水位埋深为0.5～0.7 m，低水位埋深为1.5 m。

3 近距离开挖卸荷全过程数值分析

3.1 方案设计及建模规划

上海软土地区基坑开挖对地表的影响一般不超过围护结构边缘外5H（H为开挖深度），主要影响范围在2H 以内，且受到基坑规模和长宽比的影响[7]。本文所研究的基坑平面尺寸为160 m×50 m，围护墙最深达38 m，模型水平边界取距基坑边4H，竖向边界取距围护墙底3H。

计算时，土体、高架桥、地下连续墙及钻孔灌注桩（按照等刚度原则折算为连续墙）均采用实体单元模拟，坑内、坑外均运用interface 单元模拟墙土之间的接触关系，高架桥基础采用pile 单元模拟。计算时不考虑列车动载的作用，而按照文献[8]在桥面板上施加车辆静载。

模型侧向边界采用法向约束，模型底部采用固定约束、顶面自由，高架结构约束水平法向位移。基坑及高架桥整体网格模型见图2，高架及桩基础见图3。

3.2 本构模型及计算参数

修正剑桥模型（Modified Cam-clay）对于正常固结黏土及弱超固结黏土比较适用，计算时对于土体加、卸载过程采用不同的模量，并考虑土体材料静水压力屈服特性和压硬性，被广泛应用于软土地区地基开挖分析中[9-10]。

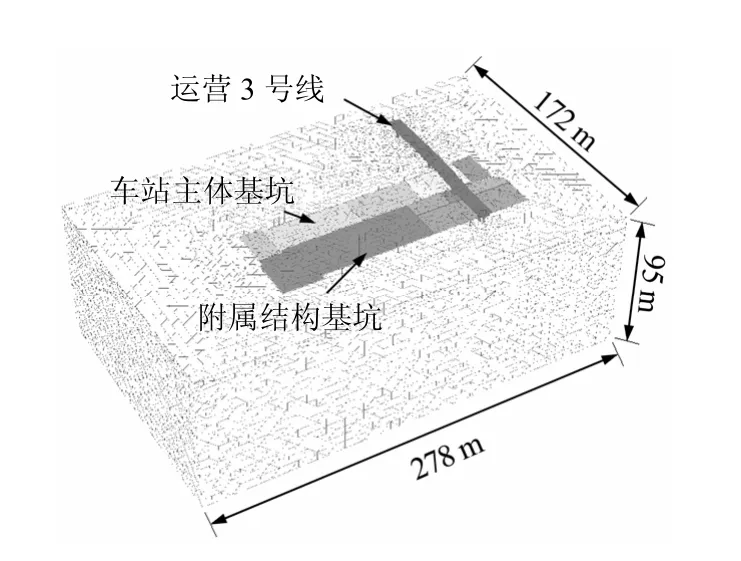
图2 模型整体网格Fig.2 Mesh of the entire model

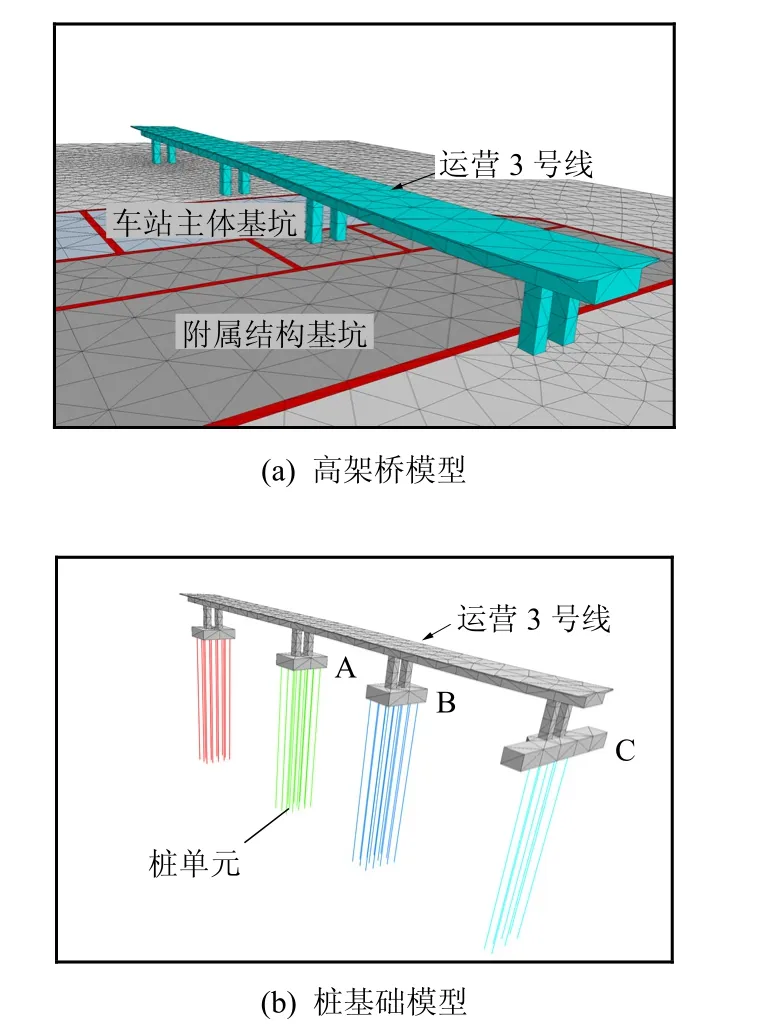
图3 高架桥及桩基础模型Fig.3 Model of metro viaduct and pile

本文将采用修正剑桥模型进行分析，该模型需要如下4 个参数：土体破坏时平均剪应力与平均应力之比值M，压缩指数λ，回弹指数κ 和泊松比υ ；与Biot 固结理论耦合，则又需增加渗透系数k。FLAC3D中修正剑桥模型所需的参数均可由上述参数计算得到，具体方法详见文献[11]。

根据勘察报告计算得到本文中土体的计算参数如表1 所示，其中λ 和k 需通过固结试验确定，如图4 所示。由试验数据，绘制e-lg p 曲线，得到各土层压缩回弹指数 cc和 cs，再换算成λ 和k[12]。

图4 土体固结试验Fig.4 Consolidation test of soil

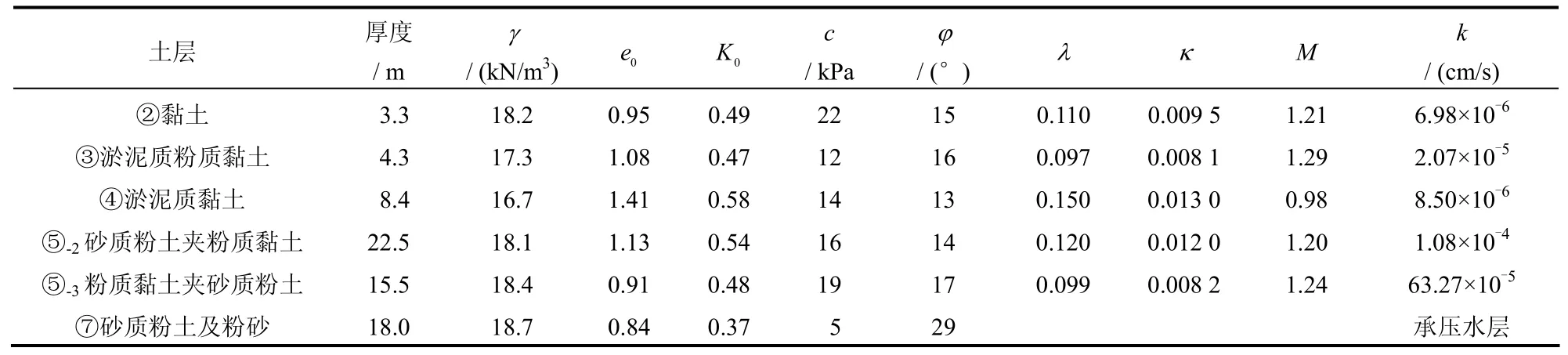
表1 土体计算参数Table 1 Parameters of soils

对于水泥加固体，施工或设计单位一般只会提供其无侧限抗压强度qu，该参数无法在数值分析中直接采用。马军庆等[13]通过对大量数据的分析，拟合得到qu与黏聚力c 和变形模量E50的关系，分别如式（1）和（2）所示，其中式（1）的单位均为kPa，式（2）的单位均为MPa。

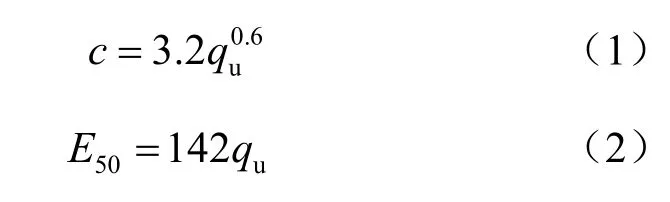
马军庆等[13]同时还给出了内摩擦角φ 的建议取值，如表2 所示。

根据本工程的设计方案，加固土 qu28≥1.2 MPa，考虑土体的不均匀性及施工因素等，淤泥质黏土中加固土取c=200 kPa，E50=150 MPa，φ=27°，粉质黏土中取φ=32°。由于加固土的类似于硬土，故采用Mohr-Coulomb 本构模型。

表2 水泥土φ 值建议取值Table 2 Suggested values of φ of cemented soils

高架、地下连续墙和其他钢筋混凝土结构采用弹性本构，弹性模量按相应混凝土等级选取。

模型中的接触面法向刚度和切向刚度参数按式（3）选取[11]。

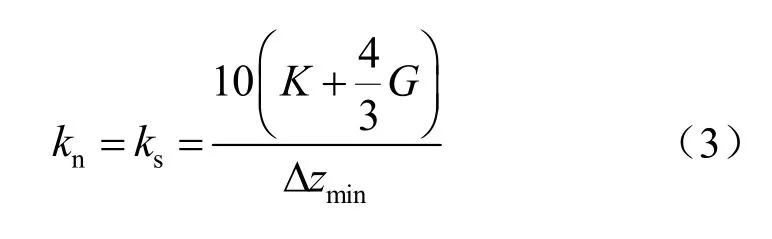
式中：K、G 分别为相邻土体的体积模量和剪切模量；Δzmin为触面法向方向上相邻网格的最小尺寸。

对于围护墙，由于其表面较为粗糙，故接触面的抗剪参数c、φ 取相邻土体的0.8 倍[14]，而对于承台，表面相对光滑，c、φ 取相邻土体的0.6 倍，不考虑接触面的抗拉强度。

3.3 基坑开挖步序

主体基坑分成3 部分开挖，由西至东依次命名为主1、主2、主3 基坑，如图5 所示。其中主3基坑在高架下段有20 m 长的逆作法区。附属基坑按照开挖先后顺序，从东至西分别为F1、F2、F3和F4。

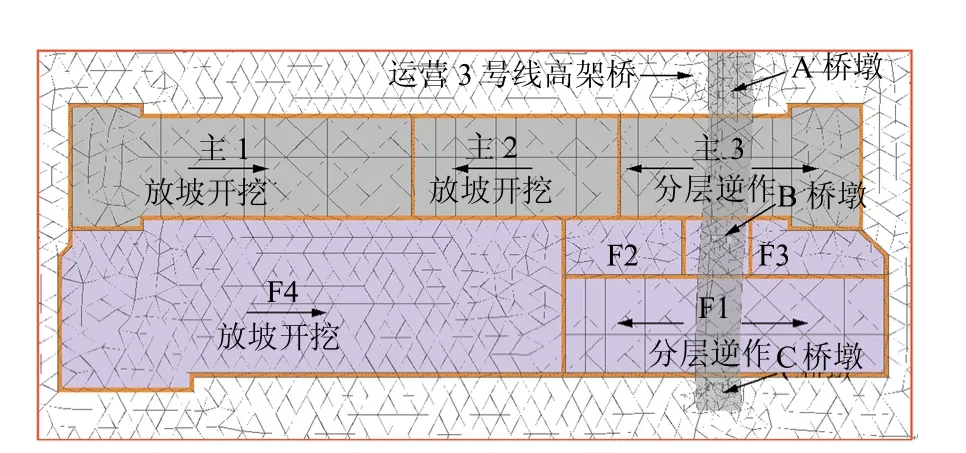
图5 基坑分块及命名Fig.5 Blocks and names of excavation

根据施工组织方案，并结合钢盖板施工及区间节点计划要求，车站基坑施工流程如下（详见图5）：

车站主体：根据盾构到达基坑的顺序，车站主体施工流程为先西区后东区：主1→主2→主3；

附属结构：先开挖F1 基坑，结构封顶后开挖F2、F3 基坑，最后开挖F4 基坑。由于F4 基坑长度较长，土方开挖从西侧开始，由西向东放坡开挖。

在数值分析时，开挖顺序完全遵循实际施工步骤，将实际的分层、分块开挖简化为分层开挖。考虑到上海地区的土质条件导致流场平衡时间远大于力学平衡，故数值分析时，每步计算均先进行力学计算，力学平衡后在打开渗流场，进行流-固耦合计算。

4 计算结果与现场实测结果对比分析

4.1 现场实测

工程施工过程中，主要监测对象为3 号线高架桥及车站的垂直位移、水平位移、同一墩台相邻立柱的差异沉降、相邻墩台两立柱的差异沉降。在高架桥墩上布设位移监测点10 点，编号GJ9～GJ18，其中GJ9～GJ14 测点同时观测水平位移。测点平面布置情况见图6，电子水平尺架在立柱横梁上。

图6 高架位移监测点布置平面图Fig.6 Displacement monitoring plan

图7 所示为主1 基坑开挖阶段GJ17～GJ18 测点的竖向位移曲线。主1 基坑标准段开挖深度H为16.8 m，距离GJ17～GJ18 两测点约64 m（＞4H），监测结果表明，两点竖向位移在±1 mm 左右波动，可以认为基坑开挖对其基本无影响，可认为此位移监测结果为3 号线正常运营引起的桥墩竖向位移。

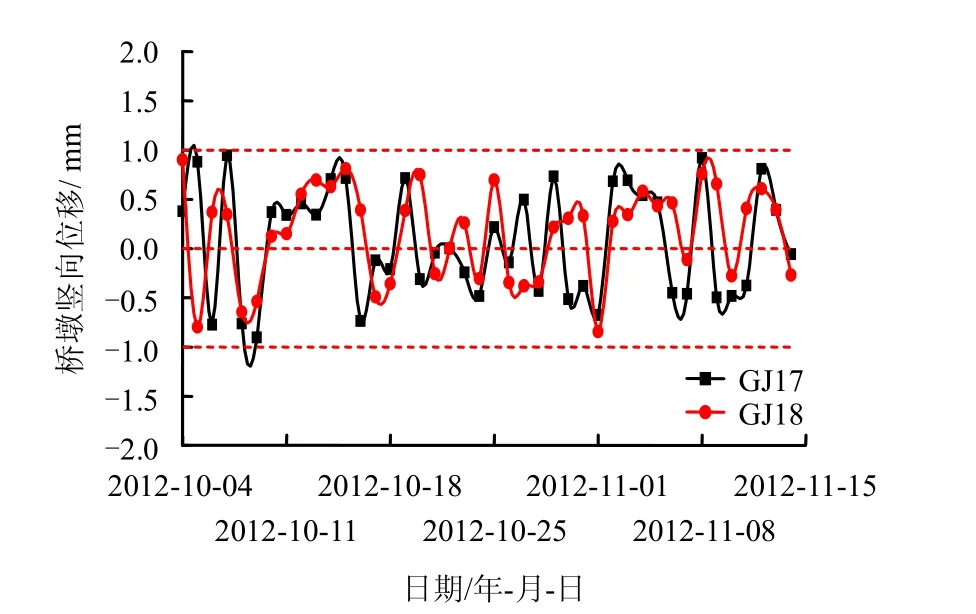
图7 主1 基坑开挖阶段GJ17、GJ18 测点竖向位移Fig.7 Vertical displacements from monitoring points GJ17 and GJ18 during Z1 excavation

图8 所示为主1 基坑开挖阶段GJ9～GJ14 测点的竖向位移曲线。主1 基坑距离高架桥墩最近为57 m（略小于4H），处于基坑开挖影响范围的边缘。与图7 中的位移曲线对比，可发现图8 中所示的桥墩竖向位移并无明显增大，仍在±1 mm 上下波动，故可以认为主1 基坑开挖对A、B、C 桥墩的竖向位移基本无影响，该阶段的监测结果可作为后续分析的位移初始值。

GJ9～GJ14 测点的水平位移监测开始于F4 基坑开挖，如图9 所示，在该阶段，桥墩水平位移表现为不规则震荡，幅度同样稳定为±1 mm。故在F4 基坑开挖及其之前的阶段，基坑开挖对桥墩水平位移几乎无影响，该阶段的位移主要由列车运行、制动等因素导致。

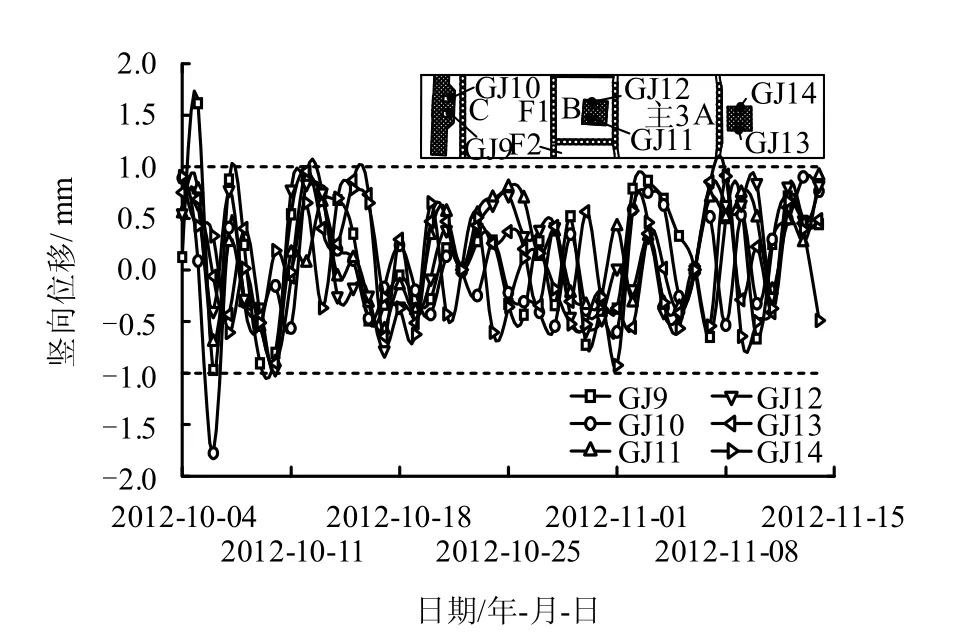
图8 主1 基坑开挖阶段GJ9～GJ14 测点竖向位移Fig.8 Vertical displacements from monitoring points GJ9-GJ14 during Z1 excavation

图9 附4 开挖阶段GJ9～GJ14 测水平位移Fig.9 Horizontal displacements from monitoring points GJ9-GJ14 during F4 excavation

主1 基坑开挖过程中，受MJS 桩施工的影响，靠近南侧附属基坑的GJ7～8、GJ9～10、GJ11～12出现一定的隆起，隆起值在5～8 mm 左右，后期有缓慢恢复，最终仍有2～5 mm 的隆起残留。由于MJS 施工是非常复杂的固、液、气三相耦合过程，且伴随着高水（气）压作用，难以在数值分析中准确考虑，故本文计算中没有考虑MJS 施工过程，仅在累计沉降监测数据中减掉由于MJS 施工引起的位移。

4.2 桥墩竖向位移

图10～12 分别为A、B、C 3 个桥墩在基坑开挖过程中竖向位移的发展情况。由于计算中没有考虑列车运营中产生的随机振动，根据图8 的监测结果，将计算结果增加±1 mm 的幅值以考虑列车振动的影响。为方便分析，在数据处理时将每个基坑的工期均匀拉长或缩短，使其在图中所占横轴的长度一致。

从图10～12 看出，虽然监测数据表现出很大的不规则性及不稳定性，但整体呈现出不同程度的隆起，计算结果基本吻合了这个趋势，在量值上的差异也较小。

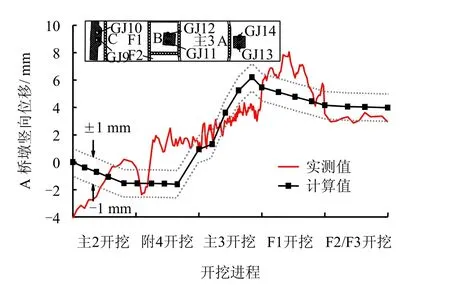
图10 A 桥墩竖向位移Fig.10 Vertical displacements of Pier A

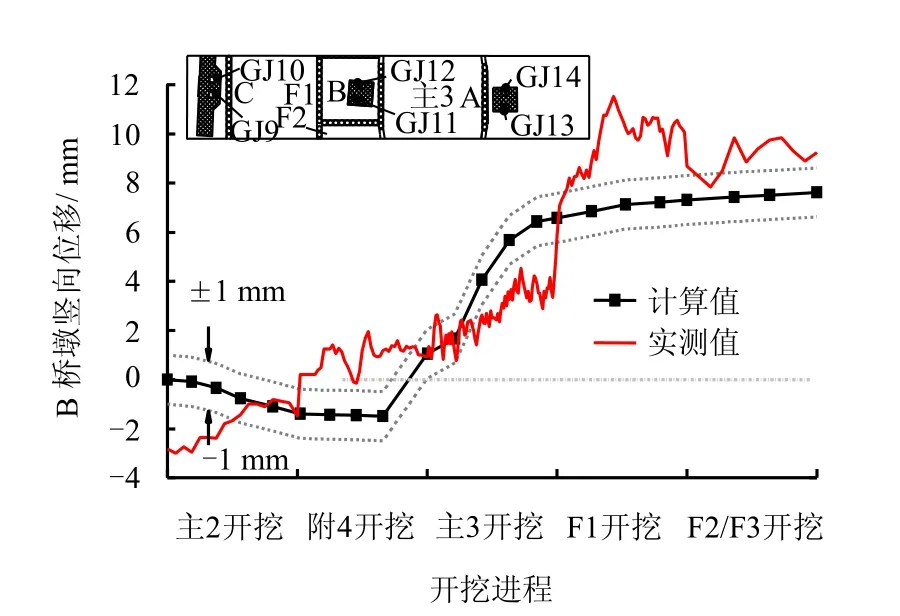
图11 B 桥墩竖向位移Fig.11 Vertical displacements of Pier B

如图10、11 所示，A、B 桥墩在主2 基坑开挖过程中均表现为沉降，计算最大值约为-2 mm，随后的附4 基坑开挖对其影响很小。计算结果表明，A、B 桥墩均处于主2 和附4 基坑的影响范围内，而附4 基坑开挖较浅且距离较远，故主2 基坑对桥墩的影响占到主导作用，表现为沉降。由于紧邻主3 基坑，A、B 桥墩受开挖卸荷影响表现为明显的上抬，至主3 基坑开挖结束时，A、B 桥墩的上抬量分别为6.2 mm 和6.4 mm；不同的是A 桥墩已经开始有下沉的趋势。从监测数据看，这个阶段A、B桥墩一直表现为上抬趋势，这与计算结果出现了差异，其主要原因是前期MJS 施工对桥墩产生了复杂的影响，计算中没有考虑这一点；但到附4 基坑开挖完成时，计算值与实测值非常吻合，说明MJS 施工对桥墩的影响是相对短暂的，后期基坑开挖仍然占到主导作用。

F1、F2、F3 基坑围绕B 桥墩，故这3 个附属基坑的开挖造成进一步卸荷，B 桥墩继续上抬，至F2、F3 基坑开挖结束时，累计上抬量计算值为7.6 mm；而此时相对远离的A 桥墩则表现为缓慢的沉降，至F2、F3 基坑开挖结束时，其上抬量已回复至4.0 mm。

图12 C 桥墩竖向位移Fig.12 Vertical displacements of Pier C

图12 所示，C 桥墩在主2、附4 和住基坑开挖过程中表现为缓慢、轻微的沉降，计算值最大约为-0.84 mm，在主3 基坑开挖至坑底标高时，由于卸载量增大，C 桥墩开始上抬。随后的F1 基坑开挖对C 桥墩产生明显影响，其上抬量计算值最大为4.6 mm；F2、F3 基坑开挖对C 桥墩影响不明显，此时C 桥墩已表现为下沉趋势。C 桥墩监测结果与计算值对比规律与A、B 桥墩类似，但上抬最大发生的时机，计算值滞后于监测值。

通过上述分析可知，虽然在数值分析中未考虑MJS 施工影响，造成了开挖初期计算值与实测值有一定的差异，但随着开挖地进行，这种差异逐渐减弱，计算值与实测值最终在趋势和量值上均吻合较好。在桥墩的上抬最大值发生的时机方面，计算时与实测值吻合较差。这些差异性表明：MJS 施工对桥墩的影响是相对短暂且能够恢复的，基坑开挖卸荷的影响仍然起主导作用。

图13 所示为桥墩的工后长期沉降预测曲线。A、C 桥墩在开挖完成时的位移量计算值分别为3.98±1 mm（监测值4.43 mm）和4.09±1 mm（监测值5.84 mm），随着卸荷作用的消散，土体内部应力重分布，A 桥墩在工后2 个月内发生沉降，随后稳定，最终位移为3.05 mm；类似地，C 桥墩在基坑完成后也发生沉降并持续到工后4 个月，随后趋于稳定，最终位移为2.22 mm。B 桥墩在基坑开挖完成时位移量计算值为7.64±1 mm（监测值9.24 mm），由于其位于基坑中部，孤岛四周均有围护结构约束，开挖卸荷的影响无法完全消散，故基坑完成后并没有发生明显的长期沉降，位移量最终为7.62 mm。3 个桥墩的长期沉降预测曲线表明，对于周围约束不显著的桥墩（A、C 桥墩），开挖卸荷造成的桥墩上抬效应会在基坑完成后缓慢减弱，但不会完全消散，桥墩最终状态为轻微上抬；对于周围约束明显的桥墩（B 桥墩），卸荷的影响很难消散，其导致的上抬效应不会减弱，桥墩最终状态为较大的上抬。

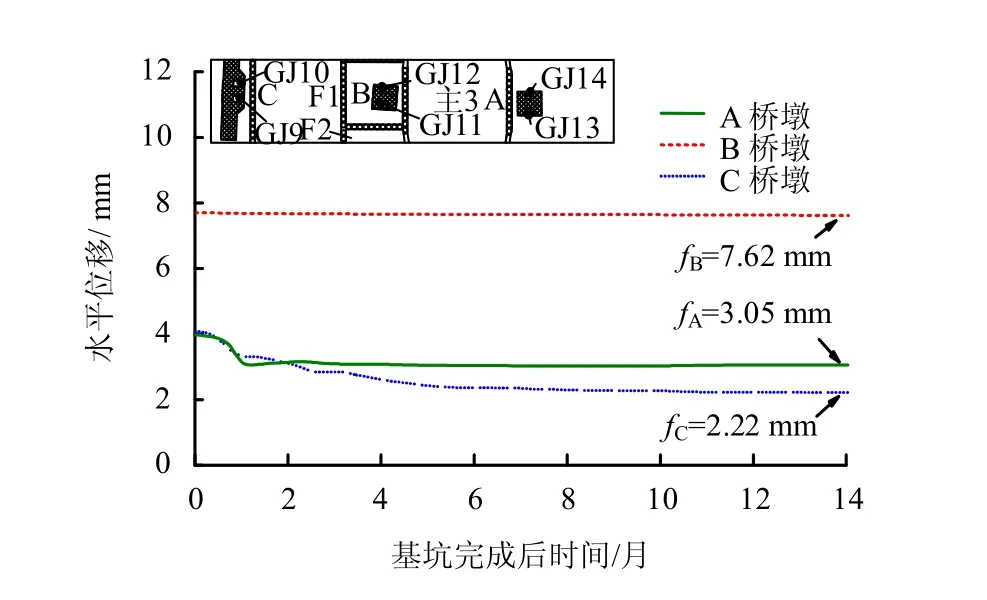
图13 桥墩长期沉降预估Fig.13 Long-term settlement estimation of piers

4.3 桥墩水平位移

本工程对A、B、C 3 个桥墩两个方向的水平位移进行了监测：垂直高架走向（X 方向）和沿着高架走向（Y 方向）。为明确表示桥墩在基坑开挖过程中的水平位移，将每个测点同一次的X、Y 方向位移组合成一个矢量，绘制于如图14～16 所示的靶形图中，图中靶心为桥墩初始位置。

如图14 所示为A 桥墩在主3 及其之后的基坑开挖引起的水平位移情况，其中空心点为桥墩位移的过程值，实心点为最终稳定值，中心填充区域为数值分析的计算值（±1 mm 以考虑随机振动）。可以看出，A 桥墩在X 方向两侧均有位移发生，沿Y方向则主要向基坑方向位移。这主要是由于实际施工中很难做到桥墩两侧的土体对称开挖，随着两侧土体交替向下开挖，土体深层位移方向不断变化，但开挖最终完成后，桥墩的水平位移为3.5 mm。在Y 方向，由于基坑开挖侧的卸荷作用，土体向基坑方向变形对桥墩约束减弱，桥墩向基坑方向位移最大值为9.5 mm，考虑X 向位移，则位移矢量大小最大已经超过12 mm，这说明基坑开挖对桥墩的影响是非常显著的。最终，随着基坑状态的稳定，桥墩位移有所恢复并稳定在4 mm 左右，桥墩整体向东侧移动，并发生轻微的扭转（GJ13 与GJ14 在Y 方向位移异号）。数值计算对桥墩的预估位移为2.44±1 mm，与监测结果基本吻合，但由于没有考虑诸如围护结构施工、止水帷幕施工、MJS 加固、开挖不对称等非开挖因素，计算结果未能反映出桥墩在施工过程中位移的发展变化过程。

图14 A 桥墩的水平位移Fig.14 Horizontal displacements of Pier A

图15 所示为B 桥墩在主3 及其之后的基坑开挖引起的水平位移发展过程。受主3 基坑开挖影响，桥墩B 总体向主3 基坑方向发展，X、Y 方向最大位移分别达到6.5 mm 和4.5 mm。随后，受F1 基坑开挖影响，B 桥墩转而向F1 基坑位移，X、Y 方向最大位移分别达到8.5 mm 和6.0 mm。在前述的两个阶段，B 桥墩有一定的侧移，随着F2/F3 基坑的开挖，B 桥墩位移向初始位置恢复，最终整体向F1基坑方向位移2.5 mm，GJ11 和GJ12 分别向两侧位移，但其中心位置仍在Y 轴附近，说明B 桥墩在X方向的位移很小。B 桥墩水平位移的数值分析结果为1.19±1 mm，小于实测值，其原因同样是数值计算未考虑非开挖因素，且B 桥墩实际卸载路径远远比数值计算的工况复杂的多，对土体的扰动也更大。

图15 B 桥墩的水平位移Fig.15 Horizontal displacements of Pier B

C 桥墩水平位移的发展如图16 所示，其表现的规律与A 桥墩类似，不同的是，由于F1 基坑开挖深度近为主3 基坑的一半，故C 桥墩水平位移值总体上也小于A 桥墩，但最终位移值与A 桥墩基本一致，未发生明显扭转；数值分析结果与实测结果吻合较好。

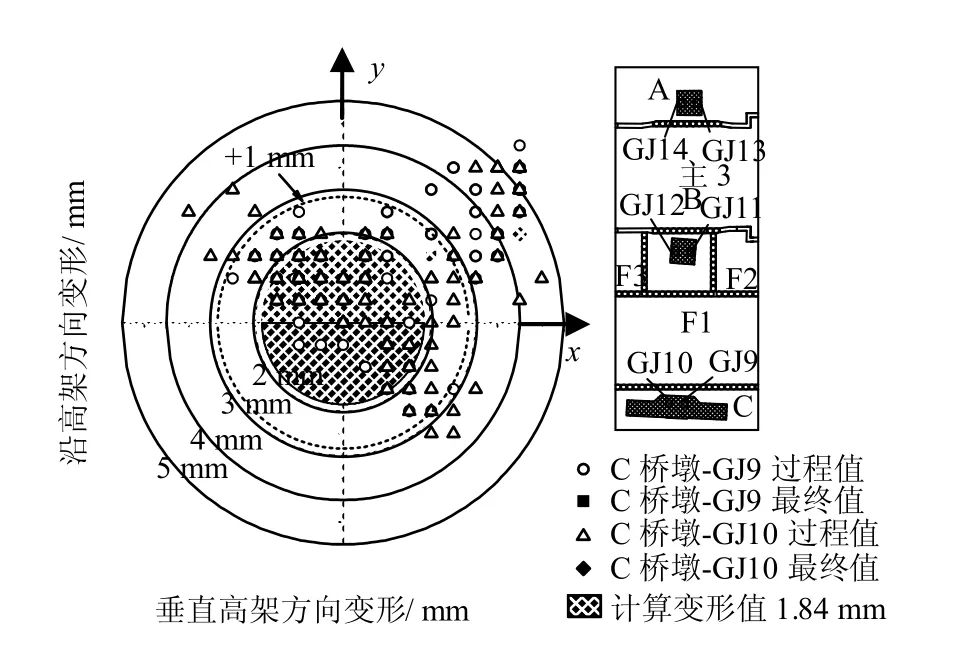
图16 C 桥墩水平位移Fig.16 Horizontal displacements of Pier C

总览图14～16，3 个桥墩水平位移的数值计算结果与实测最终值吻合度尚可，但数值分析没有反映出桥墩水平位移的发展、震荡情况。数值计算是实际施工过程和复杂因素的简化，其计算结果自然具有一定的局限性，特别是对于位移的发展过程，因此，在运用数值分析结果时，应充分考虑实际施工中多种因素的不利影响。

4.4 基础桩承载力损失

计算显示，A、B、C 3 个桥墩基础桩的侧向变形均较小（＜10 mm），故本文不对桩身变形展开分析，而是着重分析基坑开挖导致的基础桩承载力的变化。

根据《建筑桩基础技术规范》[15]，灌注桩单桩承载力特征值可由下式求得：

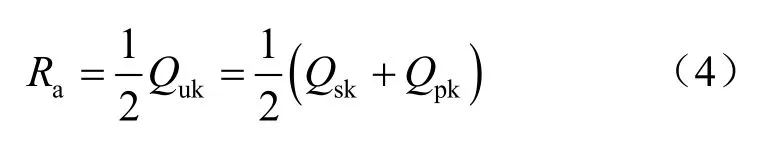
式中：Ra为单桩竖向承载力特征值；Quk为单桩竖向承载力标准值；Qsk为总极限侧阻力标准值；Qpk为总极限端阻力标准值，计算中取安全系数为2。

本文中，高架桥的基础为摩擦桩，由 Quk提供主要的承载力，并受到土体强度参数、成桩工艺等多种因素影响。实际施工中，桩-土界面很难平整（见图17），陈雨孙[16]认为，摩擦桩周围土体（I 和II）都在法向力N=K0γzz的作用下受到剪力（摩擦力）作用，其中，K0为静止侧压力系数，γz为土体重度，z为埋深。图中，w为剪切面外侧土体的弹性变形，Δw为剪切面的相对位移。

据此，总极限侧阻力标准值 Qsk可表示为

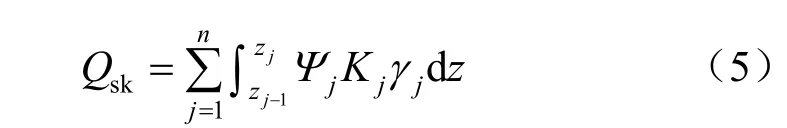
式中：Kj、γj、zj分别为第j 土的静止侧压力系数、重度和层底标高；Ψj为等效广义摩擦系数，它是影响桩-土界面摩擦力的多种因素的综合反映。假设Ψj在基坑开挖卸载过程中不发生变化，则桩-土界面上的静止土压力损失程度直接决定了摩擦桩承载力的损失。

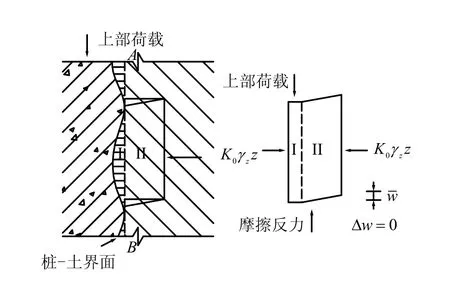
图17 桩-土界面相互作用Fig.17 Interaction between pile and soil

现场试验[17-18]、理论计算[16]及规范方法都表明，黏性土地层中桩身摩阻力并非沿桩长均匀分布，而是呈现浅部摩阻力小，深部摩阻力大的特点。为简化分析基础桩极限承载力的变化，可以保守地假设桩身摩阻力与桩身受到的静止土压力成正比，不考虑其随深度的变化，则可通过求得静止土压力损失比率曲线与坐标轴围成的面积来估算基础桩极限承载力的损失。基础桩周围静止土压力损失比例可定义为

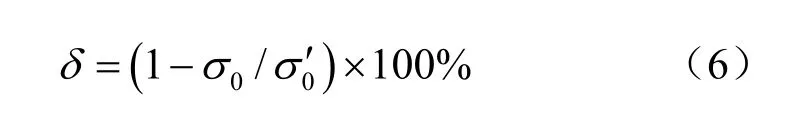
式中：σ0为基桩周围初始静止土压力；σ0′为基坑开挖后基础桩周围静止土压力。将式（6）带入式（5）并与开挖前基础桩承载力公式作比值，即可得到基础桩极限承载力的损失比例，如式（7）所示，若假设Ψj不变，则式（7）可简化为式（8），式（7）、（8）中，Qsk′为基坑开挖后桥墩基础桩的极限承载力，其他参数的含义同前。

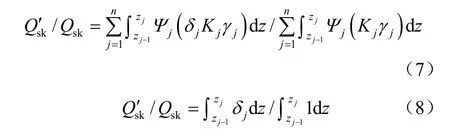
图18为计算得到的A 桥墩基础桩静止土压力损失。桥墩基础桩主要受主3 基坑开挖的影响，其静止土压力的损失主要发生在20 m 深度范围以内，最初随深度增加而增加，在13.5 m 处达到最大值22.7%，随后开始减小，在桩底标高处，静止土压力损失几乎为0。根据式（8），利用数值积分可以求得对于A 桥墩桩基的极限承载力损失为8.6%。

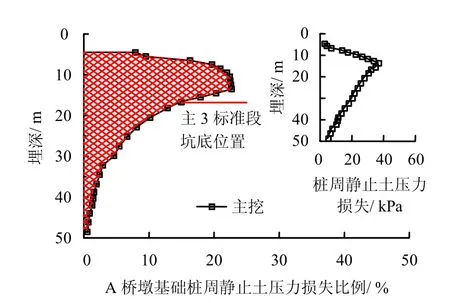
图18 A 桥墩基础桩静止土压力损失Fig.18 Static earth pressure losses of pile belonging to Pier A

图19 所示为B 桥墩基础桩静止土压力损失。B桥墩处于主3、F1、F2 和F3 共4 个基坑的包围中，属于全周开挖卸荷情况。在主3 基坑开挖后，基础桩静止土压力损失与A 桥墩表现为类似的规律，在13.5 m 处损失比例达到最大值19.3%，此时基础桩极限承载力损失为7.3%。随着F1、F2 和F3 基坑的开挖，浅部桩周静止土压力进一步损失，并在附属基坑底标高处最为严重，相应的基础桩极限承载力损失分别为8.0%和8.4%。由于在B 桥墩周围保留了一块孤岛未开挖，有效地减小了桩周静止土压力损失，使基础桩极限承载力的损失反而略小于A桥墩。

图19 B 桥墩基础桩静止土压力损失Fig.19 Static earth pressure losses of pile belonging to Pier B

C 桥墩位于F1 基坑一侧，距离主3 基坑约30 m，如图20 所示，其基础桩仍然受到主3 基坑开挖的影响。在主3 基坑开挖后，C 桥墩基础桩静止土压力损失规律与A、B 桥墩类似，在13.5 m 处达到最大值5.8%，此时基础桩极限承载力损失为2.2%。主1基坑开挖后，静止土压力进一步损失，并在其坑底标高出达到最大值10.6%，此时基础桩极限承载力损失为2.6%。由上面的分析可以看出，虽然主3 基坑没有紧邻C 桥墩，但其对C 桥墩桩基础的影响仍占主导作用，但相比于A、B 桥墩，影响程度显著降低，仅为1/3 左右。

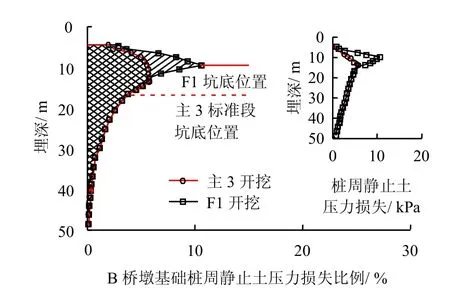
图20 C 桥墩基础桩静止土压力损失Fig.20 Static earth pressure losses of pile belonging to Pier C

从上面的分析可以看出，A、B、C 3 个桥墩坑底标高以上的部分静止土压力有比较明显的损失，在此深度以下，损失程度降低。由于基础桩较长，故由式（8）计算得到的基础桩极限承载力损失比较小，A、B、C 3 个桥墩分别为8.6%、8.4%和2.6%，考虑到设计过程中参数取值均比较保守，故小幅度的承载力损失基本不会对高架桥安全造成威胁。

5 结论与建议

（1）基坑的开挖卸荷将导致高架桥墩产生向上的位移，位移的大小与邻近基坑的开挖深度以及桥墩的卸荷程度（全周或半周）有关，基坑开挖深度越大、卸荷越多，则上抬变形越大。

（2）由于非开挖因素对桥墩水平位移影响的方向不一致，高架桥墩水平位移在基坑开挖过程中震荡明显，总体趋势为朝向卸荷一侧位移，垂直高架走向的位移相对较小。桥墩水平位移数值计算结果与实测终值吻合度尚可，但没能反应位移发展过程。

（3）长期沉降计算表明，对于半周卸荷情况（A、C 桥墩），上抬位移在后期有一定的恢复；对于全周卸荷情况（B 桥墩），则不会恢复，其长期位移仍然保持较大的上抬。

（4）基坑开挖卸荷将导致基础桩周围静止土压力损失，特别是坑底标高以上部分；由此导致基础桩极限承载力产生损失，开挖越深，损失越大，但均小于10%，该程度的损失基本不会对高架桥安全造成威胁。

（5）数值分析对实际施工进行了简化，未考虑MJS 施工过程、开挖无法完全对称等因素，计算结果表明，数值计算可以较好地预估桥墩竖向位移的趋势和位移量；但在桥墩水平位移方面，仅能对位移终值进行相对合理地预估，无法反应水平位移的发展过程。应用数值分析结果时，应充分考虑其局限性，以确保工程安全。

[1]朱炎兵,周小华,魏仕锋,等.临近既有地铁车站的基坑变形性状研究[J].岩土力学,2013,34(10):2997－3002.ZHU Yan-bing,ZHOU Xiao-hua,WEI Shi-feng.et al.Investigation on deformation behaviors of foundation pit adjacent to existing metro stations[J].Rock and Soil Mechanics,2013,34(10):2997－3002.

[2]殷德顺,王保田,张文慧.不同方向卸载对基坑支护位移内力的影响[J].岩土力学,2008,9(6):1701－1705.YIN Shun-deng,WANG Bao-tian,ZHANG Wen-hui.Influences of different directional unloadings upon displacements and internal forces of retaining structure for foundation pit[J].Rock and Soil Mechanics,2008,9(6):1701－1705.

[3]LIU G B,NG C W W,WANG Z W.Observed performance of a deep multistrutted excavation in Shanghai soft clays[J].Journal of Geotechnical and Geoenvironmental Engineering,2005,131(8):1004－1013.

[4]张羽.基坑开挖与邻近桩基础的相互影响分析[D].上海:同济大学,2007.ZHANG Yu.The Analysis of interaetion between excavation of foundstion pit and nearby pile foundation[D].Shanghai:Tongji University,2007.

[5]丁勇春,王建华.深基坑施工对高架基础的变形影响及控制研究[J].土木工程学报,2012,45(7):155－161.DING Yong-chun,WANG Jian-hua.Influence of deep excavation on deformation of elevated bridge foundations and counter-measures[J].China Civil Engineering Journal,2012,45(7):155－161.

[6]王成华,刘庆晨.考虑基坑开挖影响的群桩基础竖向承载性状数值分析[J].岩土力学,2012,33(6):1851－1856.WANG Cheng-hua,LIU Qing-chen.Numerical analysis of vertical bearing behavior of group pile foundation considering pit excavation effect[J].Rock and Soil Mechanics,2012,33(6):1851－1856.

[7]丁勇春.软土底层深基坑施工引起的变形及控制研究[D].上海:上海交通大学,2009.DING Yong-chun.Excavation-induced deformation and control in soft deposits[D].Shanghai:Shanghai Jiaotong University,2009.

[8]上海市隧道工程轨道交通设计研究院.DGJ08－109 城市轨道交通设计规范[S].上海:上海市城乡建设和管理委员会,2004.Shanghai Tunnel Engineering &Rail Transit Design and Research Institute.DGJ08－109 Urban rail transit design standard[S].Shanghai:Shanghai Urban Construction and Communications Commission,2004.

[9]徐中华.上海地区支护结构与主体地下结构相结合的深基坑变形性状研究[D].上海:上海交通大学,2007.XU Zhong-hua.Deformation behavior of deep excavations supported by permanent structure in shanghai soft deposit[D].Shanghai:Shanghai Jiaotong University,2007.

[10]王清,郭惟嘉,刘正兴.修正剑桥模型在基坑开挖分析中的应用[J].上海交通大学学报,2001,35(4):565－569.GUO Qing,GUO Wei-jia,LIU Zheng-xin.Application of modified cambridge model in foundation excavation[J].Journal of Shanghai Jiaotong University,2001,35(4):565－569.

[11]Itasca Consulting Group,Inc..Fast Lagrangian Analysis of Continua in 3 Dimensions:Theory and background,Version 3.0,Users' Manual[M].[S.l]:Minneapolis,2002.

[12]朱百里,沈珠江.计算土力学[M].上海:上海科学技术出版社,1990.ZHU Bai-li,SHEN Zhu-jiang.Calculation of soil mechanics[M].Shanghai: Shanghai Science and Technology Press,1990.

[13]马军庆,王有熙,李红梅,等.水泥土参数的估算[J].建筑科学,2005,25(3):65－67.MA Qing-jun,WANG You-xi,LI Hong-mei,et al.Study on the relations of cement-soil parameters with compressive strength[J].Building Science,2005,25(3):65－67.

[14]胡黎明,濮家骝.土与结构物接触面物理力学特性试验研究[J].岩土工程学报,2001,23(4):431－435.HU Li-ming,PU Jia-liu.Experimental study on mechanical characteristics of soil-structure interface[J].Chinese Journal of Geotechnical Engineering,2001,23(4):431－435.

[15]中华人民共和国住房和城乡建设部.JGJ 94 建筑桩基础技术规范[S].北京:中华人民共和国住房和城乡建设部,2008.Ministry of Housing and Urban-Rural Development of the People's Republic of China.JGJ 94 Technical code for building pile foundations[S].Beijing:Ministry of Housing and Urban-Rural Development of the People's Republic of China,2008.

[16]陈雨孙.纯摩擦桩荷载-沉降曲线的拟合方法及其工作机理[J].岩土工程学报,1987,9(2):49－61.CHEN Yu-sun.The mechanism and fitting method of loading-settlement curve of pure friction pile[J].Chinese Journal of Geotechnical Engineering,1987,9(2):49－61.

[17]杨宇,马晔,宋春霞.中风化花岗岩层与基桩侧摩阻性能现场试验研究[J].岩石力学与工程学报,2013,32(1):97－106.YANG Yu,MA Ye,SONG Chun-xia.In-situ test research on side friction of bridge piles in moderate weathered granite[J].Chinese Journal of Rock Mechanics and Engineering,2013,32(1):97－106.

[18]宋兵.桩侧摩阻力特性的研究[D].广州:华南理工大学,2010.SONG Bing.Study on the characteristies of shaft soil resistance of pile[D].Guangzhou:South China University of Technology,2010.