抓问题特征，简单解答求数列通项公式问题

（酒泉师范学校735000）

抓问题特征，简单解答求数列通项公式问题

朱 鸿（酒泉师范学校735000）

抓问题特征，简单解答求数列通项公式的问题。

数列特征求法

求数列的通项公式是学习数列知识的难点，通常表现出来的问题是教师讲解，学生能听懂，但遇到问题学生不会自己解答。这主要是学生对求数列通项公式问题的特征没有很好的把握，见了问题辨认不清造成的。要很好地解决这个问题，首先应掌握问题的特征，然后再掌握求解的思路和方法。下面笔者就一些常见的简单的求数列通项公式问题的解答略作总结。

一、观察数列中各项的特征，求数列的通项公式

这类问题的特征是给出一个数列的前几项，求数列的通项公式。一般在给出的前几项中，存在着丰富的信息，对此，我们只要抓住最具特征的信息，以此为突破口，就能很容易地找到第n项an与项数n之间的关系，求出通项公式。

二、利用等差或等比数列的通项公式，求数列的通项公式

这类问题的特征是数列是等差数列或等比数列，是求数列通项公式中最简单的一类问题，根据等差数列或等比数列的通项公式求解即可。

三、利用an与Sn之间的关系，求数列的通项公式

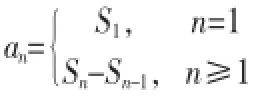
第一步：当n=1时，a1=S1；

第二步：当n≥2时，an=Sn-Sn-1；

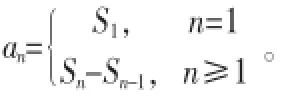
解：（1）当n=1时，a1=S1=3

当n≥2时，an=Sn-Sn-1=2n+1

把n=1代入n≥2时的通项，得a1=3=S1，所以，an=2n+1。

（2）当n=1时，a1=S1=6

当n≥2时，an=Sn-Sn-1=2n+1

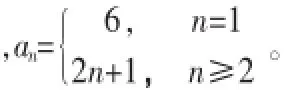
（2）当n＝1时，10a1＝10S1＝a21+5a1+6，解之，得a1＝2或a1＝3。

当n≥2时，10an＝10Sn-10Sn-1＝a2n+5an+6-a2n-1-5an-6

即（an+an-1）（an-an-1-5）＝0

又∵a1，a3，a15成等比数列∴an＝5n-3

∴｝的前n项和为Sn，满足4Sn＝a2n+1-4n-1，n∈N*且a2，a5，a145构成等比数列,求数列an｛｝的通项公式。

解：当n＝1时，4a1＝4S1=a22-5,a22=4a1+5，

当n≥2时，即4an＝4Sn-4Sn-1=a2n+1-a2n-4，a2n+1=（an+2）2

∵an＞0∴an+1＝an+2∴n≥2时，数列an｛｝是等差数列。

又∵a2，a5，a14是等比数列,∴a25＝a2a14，即（a2+6）2＝a2（a2+24），解得a2＝3

又a22＝4a1+5∴9＝4a1+5，a1=1∴a2-a1＝2∴an｛｝是等差数列

∴an＝2n-1

四、已知数列的递推公式，求数列的通项公式

已知数列的递推公式，求数列的通项公式时，要求记住三点：记住递推公式的特征；记住求解思路；记住求解方法，最关键是记住递推公式的特征。

（一）已知数列｛an｝的首项a1及递推公式an+1= an+f（n），求通项公式

1．递推公式特征：an+1=an+f（n）；

2．求解思路与求解方法：累加法或叠加法。

例5在数列｛an｝中，已知a1=1，当n≥2时，an＝an-1+2n+1，求数列｛an｝的通项公式。

解：当n≥2时，

an＝a1+（a2-a1）+（a3-a2）+…+（an-an-1）＝1+3+ 5+…+（2n-1）＝n2

把n＝1代入上式，得a1＝1，与已知相符，所以an＝n2。

1．递推公式特征：an+1＝f（n）an。

2．求解思路与求解方法：累乘法或叠乘法。

例6在数列｛an｝中，已知a1＝1，当n≥2时, nan-1＝（n+1）an，求数列｛an｝的通项公式。

（三）已知数列的一元二次字母系数方程，通过解方程得出递推公式an+1＝f（n）an，再利用累乘法求出数列｝的通项公式。

例7在各项均为正数的数列an｛｝中,a1＝2,，求an。

把n＝1代入上式，得a1＝2，与已知相符，所以an＝2n。

（四）已知数列an｛｝的首项a1及递推公式an+1＝pan+q（p≠0且，p≠L,q≠0），求通项公式

1.递推公式特征：an+1＝pan+q（p≠0且，p≠L, q≠0）。

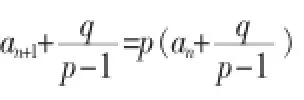
例8已知数列an｛｝的通项。(an＝2n+1-3)

解：递推公式可化为an+1+3＝2（an+3）∴数列｛｝中，a1＝1，2an+3求数列an an+3｛｝的首项a1及递推公式an+1＝ManN（an＞0，M＞0），求通项公式

1.递推公式特征：an+1＝ManN（an＞0，M＞0）2.求解思路与求解方法：通过两边取对数｛｝是首项为4等比数列。

∴an+3＝2n+1∴an＝2n+1-3

例9已知数列an｛｝满足a1＝c＞0,an+1＝an3+ 3an2+3an（n∈N*）求数列的通项公式。

解：递推公式可化为an+1+1＝（an+1）3……（1）

∵a1＞0∵a1＝c＞0,an+1＝an3+3an2+3an（n∈N*），∴an＞0

∴给（1）两边对数，得lg（an+1+1）＝3lg（an+1）

∴lg（an+1+1｛｝）是公比为3，首相为lg（c+1）的等比数列

∴lg（an+1）＝lg（c+1）3n-1＝lg（c+1）3n-1∴an+1＝（c+1）3n-1-1

（六）已知数列an｛｝的首项a1及递推公式an+1＝pan+qn（pq(p-1)（q-1）≠0），求通项公式

1.递推公式特征：an+1＝pan+qn（pq(p-1)（q-1）≠0）。

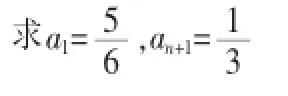
1.递推公式特征：an+2＝pan+1+qan（p,q均为常数）

2.求解思路与求解方法：利用待定系数法，即令原递推公式可化为an+2-San+1＝t(an+1-San)的形式，构造一个以t为公比的等比数列an+1-San

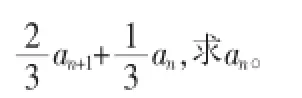
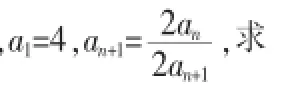
（责编 赵建荣）