面向绿色制造的机床主轴加工工艺路线优化

臧维娜， 高国生

（石家庄铁道大学 机械工程学院，河北 石家庄 050043）

0 引言

绿色制造是一种现代化的制造方式，这种制造方式充分考虑到制造业对生态环境的破坏以及对能源资源的使用效率。绿色制造要求产品在设计、制造、运输、销售以及使用的整个过程中，实现对资源的充分利用，使资源的利用率达到最高程度，将环境破坏的程度降低到最小范围［1］。绿色制造的研究包括绿色设计、绿色工艺、绿色包装、绿色回收处理等技术领域。其中绿色工艺与零件制造过程直接相关，工艺路线的优劣更对工艺的合理与否占有重大影响。纵观国内外研究现状，目前在绿色制造工艺路线优化方面己经取得了一定结果，所采用的优化方法主要集中在遗传算法［2－5］上。工艺路线优化属于NP－hard问题［2］，遗传算法是一种启发式非数值并行算法，它对优化对象既不要求连续，也不要求可微或其他辅助知识，尤其适合求解NP－hard问题［6］，但由于工艺路线的排序并非任意，需满足一定的约束条件，采用遗传算法在寻优过程中往往存在大量不合理路线，出现冗余迭代，致使求解效率降低。鉴于此，本文以机床主轴为例，利用分组拓扑排序法对主轴加工工艺约束有向图进行简化，并通过全拓扑排序直接生成所有满足约束的可行工艺路线集，然后根据优化目标进行评判，从而找到最优工艺路线。这种方法避免了对变异序列合法性的逐个验证，进一步提高了求解效率，特别适用于工艺约束条件较多的复杂零件的工艺路线排序优化。

1 工艺优先约束

合理的加工工艺路线制定必须满足加工特征和加工方法间的优先关系约束，主要包括以下几个方面：

（1）先粗后精。即先粗加工，再半精加工，最后安排精加工或光整加工。

（2）先主后次。即主要表面先加工，后安排次要表面加工，一般情况下，次要表面安排在最后的精加工或光整加工之前。

（3）基准面先于其它面加工。两个加工特征间存在形位公差关系时，包含基准的加工特征首先加工。如果基准面不只一个，则按照基准面转换的顺序和逐步提高加工精度的原则来安排加工。

（4）紧邻次序约束。对于加工机床、刀具、夹具以及加工阶段均相同的两工序，在无特别因素影响下，要求其加工顺序邻接，以减少不必要的变换次数。

（5）非破坏性约束。保证后面的加工不会破坏前面加工过程中产生的属性。

图1为一机床主轴零件图，由图1可知，主轴呈阶梯状，主要加工表面包括两个支承轴颈、前端短锥面及其端面、锥孔，以及安装齿轮的各个轴颈等。非主要表面包括螺孔、螺纹、键槽等。因不易出现废品，这些表面的加工顺序应尽量排后，但为了防止其在加工过程中损伤主要表面，所以应安排在主要表面最终精加工工序之前。根据基准选择原则，应以主轴两端的顶尖孔为精基准面。所以在粗车加工主轴之前应以前、后支撑轴颈为粗基准优先加工顶尖孔。加工过程中，为了保证支承轴颈与内锥面的同轴度要求，宜按互为基准原则选择基准面［7］。在此，因支承轴颈为外锥面，不宜装夹，可选择与支承轴颈相邻而且又是同一基准加工出来的外圆柱面为定位准面。据上述内容，得出主轴加工单元间优先关系，如表1所示。

图1 机床主轴零件图（单位：mm）

表1 加工单元间优先关系

2 工艺约束有向图分组拓扑排序和全拓扑排序实现

2．1 工艺约束有向图

在约束规则下，加工单元间的优先关系约束表现为执行的先后顺序。工艺路线排序过程实际上就是将约束逐个作用到加工特征单元集合上，使得加工方法在一定的排列顺序下，目标函数值最优［2］。由于描述性的、定性的约束信息在计算机处理时较为复杂，不便于计算机的底层推理与简化计算，在遵循约束规则下，本文通过绘制工艺约束有向图来表示零件的多工艺路线，并以邻接矩阵的方式来存储加工单元间的优先关系约束，将定性的优先关系约束信息转化为定量的、数字化的矩阵来表达。

有向图是由单元顶点集合和顶点间的关系集合组成的一种数据结构：Graph＝（V，E），这种有向图也通常被称为AOV 网。对工艺有向图而言，V 表示加工某零件需要的加工方法（工序或工步）的有穷非空集合，在此称为加工单元集；E 是加工单元顶点间关系的有穷集合，也叫做边集合，其存储的是加工单元间的优先关系。Graph的邻接矩阵A 按如下方式定义

如果顶点i到顶点j 间存在有向边，则称顶点i为顶点j 的前趋，也可以说顶点j是顶点i 的后继。当两顶点之间没有直接或间接的有向连线时，表明两顶点间没有优先关系。在绘制工艺约束有向图时，为了表达明确、便于后期处理，对没有唯一起点的有向图设置一个虚拟最前顶点，对于图中未涉及到的加工单元，通过有向边从虚拟最前顶点连接到该单元，对于由多个有向图描述的优先关系，也通过虚拟最前顶点连接各有向图。如图2所示为工艺约束有向图的建立方法，加工单元序号从2到11，1为虚拟最前顶点。按照此方法建立主轴加工工艺约束有向图，如图3所示。

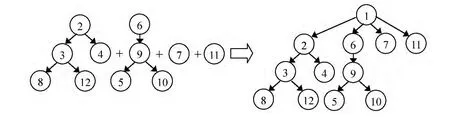
图2 工艺约束有向图建立方法

图3 主轴加工工艺约束有向图

2．2 全拓扑排序实现

求一个AOV 网的所有拓扑排序序列即为全拓扑排序，在此用一维数组分别存储排序过程中各顶点的入度值和输出情况，用栈结构临时存储排序序列，矩阵存储全部序列，其方法如下：

（1）选择一个入度为0的顶点，并输出入栈（按照顶点标号由小到大决定入栈次序）；

（2）对该顶点的直接后继顶点的入度值减1；

（3）如存在入度为0的顶点，则重复步骤（1）（2），否则序列完成，存储该序列；

（4）栈顶顶点出栈，删除输出状态；

（5）对该顶点的直接后继顶点的入度值加1；

（6）如存在其它入度值为0的顶点（只考虑标号值大于该顶点的顶点），输出一个并入栈，重复步骤（2）（3）；如不存在则重复步骤（4）（5）；

（7）栈空时结束。

通过上述方法，对主轴加工工艺约束有向图进行全拓扑排序，最终得到的可行路线条数为16 800条，因为数量较大，运算效率低，不便于评价，所以需要对有向图进行简化处理，以减少可行路线。减少路线的方法通常有两种，一是在顶点间増加有向边，二是减少顶点数即合并顶点，具体方法按实际应用来选择。由于工艺约束有向图的有向边表示工序间的先后顺序约束，后期不能再随意添加，在此选择方法二，即对加工单元进行合并，但应注意的是并非任意两顶点都可以合并，只有在排序序列中可以相邻的两顶点才能合并，为此提出分组拓扑排序方法［6］。

2．3 分组拓扑排序方法

对有向图G＝（V，E）的结点集V 进行分组，设V＝G1∪G2∪…Gm且Gi∩Gj＝Ø（i≠j），若序列：G1，G2，…，Gm满足如下条件：Gk（k＝2，…，m）中任何结点存在前驱结点，且前驱结点必在Gk－1中，则称序列G1，G2，…，Gm为有向图的分组拓扑序列［8］。

对有向图进行分组拓扑排序的具体方法如下：

如果某顶点没有前驱顶点，即入度为0，则把这些顶点作为拓扑排序的第一组输出，第一组的顶点输出后，删除从该组顶出发的所有有向边，由此产生新的入度为0的顶点作为第二组顶点输出，如此循环直到输出最后一个顶点。

经上述方法进行分组拓扑排序后，同组中的顶点之间不存在约束，为并行关系，相邻组中的顶点存在直接先后顺序约束，即任意两点间没有强制输出顶点，在排序序列中可以相邻，这对不相邻组中两顶点来说则不完全成立，如图4为主轴加工工艺有向图分组拓扑排序结果，顶点6和顶点10在排序序列中就不能相邻。因此，选择同组或相邻组的元素对顶点进行合并，合并依据按优化目标而定。合并后将两顶点视为一个顶点进行全拓扑排序，路线优选好之后再对合并顶点顺序进行优选，最终即可得到完整的最优工艺路线。

图4 主轴加工工艺有向图分组拓扑排序

3 机床主轴工艺路线优化目标及结果

3．1 工艺优化目标函数

所谓绿色制造，是要综合考虑制造过程中成本、时间、质量、资源消耗以及环境污染五个方面的影响，因此面向绿色制造的加工工艺路线优化理论上应该以成本最低、时间最小、质量最优、资源消耗最少、环境影响最小为目标。在加工方法确定的情况下，加工过程中采用的加工顺序不同，产生的加工时间、加工费用和能量消耗也是不同的［3］。假设所选机床均能满足加工质量要求，对于可选工艺路线来说，加工成本与加工时间不同是由于对各表面加工所需机床、刀具、夹具的不同而导致的变换成本（包括运输成本、人工成本等）和时间消耗差异。机械加工系统的资源消耗包括物料消耗和能量消耗，其中物料消耗主要决策于工艺加工设计阶段，机械加工中的能量消耗则主要来源于加工过程中的电能消耗。因此，在确定了各加工单元的加工方法、定位基准以及加工资源后，把成本、时间和资源消耗作为优化目标，其中时间以时间成本一并计入成本中。

用一维数组存储加工单元编号，数组元素的顺序即代表对应加工单元在工艺路线中的顺序。令满足约束集合的加工单元工艺排序的定义域为X，上述各分目标经过归一化处理得到相应的目标函数，表示为

式中，

据上述内容，可进行优化的加工成本包括机床变换成本（MCC）、装夹变换成本（SCC）和刀具变换成本（TCC），则FC（x）可表示为

式中，

式中，n为加工单元总数，MCCI为机床变换成本指数，表示在加工过程中，若顺序相邻的两加工单元需要在不同机床上加工，则变换一次所需的成本。同理SCCI为装夹变换成本指数，TCCI为刀具变换成本指数，M、S、T 分别表示机床、夹具和刀具。θ（Xi＋1－Xi）为变换判断函数，表示如下

3．2 优化求解

［2］，令MCCI为160，SCCI为100，TCCI 为25，和应根据企业实际加工需求来制定，在此初步设为60%，40%，因给成本分配的权重值较高且其中机床变换成本最高，对加工工艺有向图进行分组拓扑排序后，对邻组加工单元进行检测，将使用机床相同的两加工单元合并成为新加工单元，并重新绘制工艺约束有向图，如图5所示。

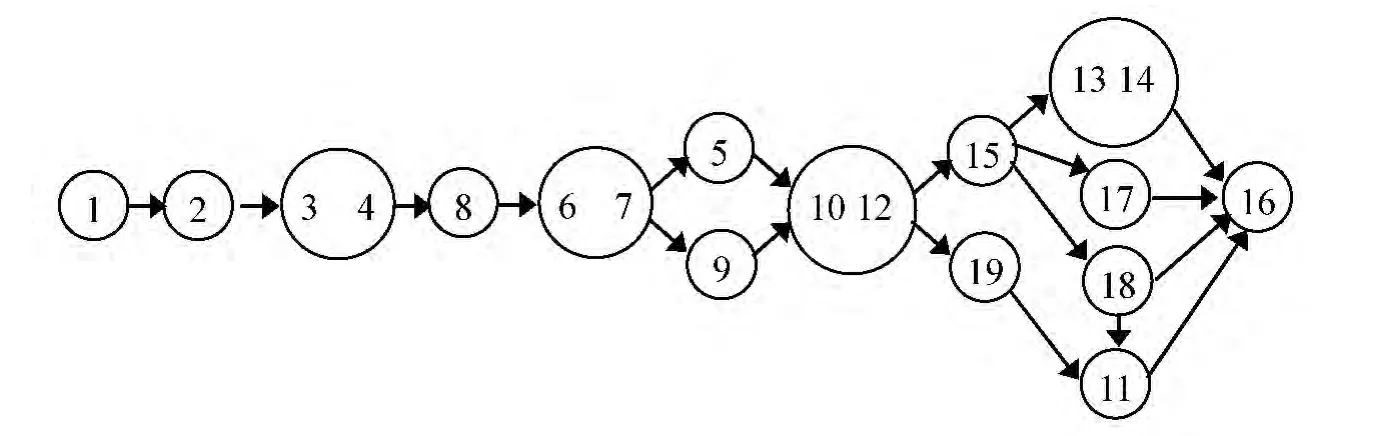
图5 简化后的主轴加工工艺约束有向图

完成后重新编排加工单元序号进行全拓扑排序，得到可行路线条数为104条，相比之前排序得到的16 800条，复杂度明显降低，根据优化目标进行评价，按照公式（2）计算各路线的目标函数，依据所得数据的最小值得到初步最优路线为：1－2－3，4－8－6，7－9－5－10，12－19－15－18－17－13，14－11－16，然后对合并的加工单元进行优化排序，依旧根据目标函数值的大小，选取目标函数最小值对应的加工路线为最优工艺路线，结果为：1－2－3－4－8－6－7－9－5－10－12－19－15－18－17－14－13－11－16，在该路线中，机床变换12次，刀具变换3次，能量消耗为7 337．124 kJ。

4 结语

工艺路线决策与优化是CAPP系统的难点与重点。本文提出通过工艺约束有向图的分组拓扑排序和全拓扑排序方法得出满足约束规则的全部可行路线集，并以最小变换成本、最低能量消耗为目标得出主轴加工的最优工艺路线，该方法简单，应用效率高，并且由于是对所有的可行路线进行加工评价，使得评价数据完整，结果清晰明了，通过选取综合目标值最优的序列可以得到较好的加工工艺路线，该方法相对于遗传算法而讲，避免了产生局部最优解，结果更为精确。对于工艺过程来讲，工艺优化是极其复杂的，其中，切削参数、机床、刀具、夹具的选择均与决策过程相关，若想得到一条更为完善的加工工艺路线，每一部分的优化选择都需要进行考虑，因此今后还需要对工艺路线所涉及的各方面进行整合优化，得出更为系统完整的优化方法。

参 考 文 献

［1］艾永旭．浅析绿色制造工艺在机械加工中的应用［J］．中国新技术新产品，2013（2）：92．

［2］王忠宾，王宁生，陈禹六．基于遗传算法的工艺路线优化决策［J］．清华大学学报：自然科学版，2004，44（7）：988－992．

［3］谭显春，刘飞，曹华军．绿色制造中的一种工艺路线决策模型及其求解算法［J］．机械工程学报，2004，40（4）：154－159．

［4］ZHANG F，ZHANG Y F．Using genetic algorithms in process planning for Job Shop machining［J］．IEEE Transactions on Evolutionary Computation，1997，1（4）：278－289．

［5］范顺成，王进峰，李世杰．基于遗传算法的工艺路线决策与优化［J］．制造技术与机床，2012（3）：95－99．

［6］黄伟军，蔡力钢，胡于进，等．基于遗传算法与有向图拓扑排序的工艺路线优化［J］．计算机集成制造系统，2009，15（9）：1770－1778 ．

［7］韩兴国．机床主轴加工工艺教学案例分析——以CA6140车床主轴机械加工为例［J］．桂林航天工业高等专科学校学报，2009（2）：211－214．

［8］舒芳，王洪发．基于组的拓扑排序［J］．赣南师范学院学报，2003（3）：18－20．