连续刚构桥跨中下挠的影响因素分析

杨晋文

（中铁十六局集团 第五工程有限公司，河北 唐山 063000）

0 引言

随着我国交通事业的蓬勃发展，大跨度预应力混凝土连续刚构桥以其施工方便、跨越能力强、结构刚度大、行车平顺、养护方便等一系列优点得到广泛应用。但是跨中长期下挠成为大跨度预应力混凝土连续刚构桥的通病。

混凝土的收缩徐变存在较大的不确定性，是一个复杂且难以精确计算的非线性问题。虽然许多学者对混凝土收缩与徐变进行了长期研究，计算理论和方法也在不断改进，但是收缩徐变对结构性能的影响至今仍难以准确计算［1］。因此在考虑混凝土徐变效应分析时，利用大型有限元软件对混凝土徐变进行模拟十分必要。本文通过建立有限元模型得出收缩徐变、应力差对高速铁路桥、高速公路桥跨中长期下挠的影响规律。

1 工程概况

高速公路连续刚构桥——贺坪峡大桥，全长310 m，位于河北省邢台市贺家坪村。主桥为80＋150＋80 m 三跨预应力混凝土连续刚构箱梁，跨中梁高3．3 m，顶板厚28 cm；墩顶箱梁顶板加厚至50 cm，底板厚从跨中至根部由32 cm 变化为110 cm；腹板从跨中至根部分3段采用50 cm、65 cm、85 cm3种厚度；箱梁高度和底板厚度均按二次抛物线变化。箱梁顶板横向宽14．13 m，底宽7．5 m，翼缘悬臂长3．315 m。箱梁0号节段长14 m，每个悬浇“T”纵向对称划分为18个节段，梁段数及梁段长从根部至跨中分别为10×3．5 m、8×4 m，节段悬浇总长为67 m。贺坪峡大桥整体布置见图1。

高速铁路连续刚构桥——南庄特大桥，南庄特大桥全长0．980 8 km，位于山西省介休市遐壁村。该连续刚构设计孔跨布置56＋104×2＋56 m，其中两跨104 m，主墩为8＃、9＃和10＃墩。0号段长14 m，中支点处梁高7．85 m，端部梁高4．85 m，截面采用单箱单室直腹板形式。顶板厚为40 cm，腹板厚130 cm，底板厚度根部为150 cm。顶板宽度12 m，底板宽度6．8 m。主桥采用三向预应力混凝土变截面连续刚构，箱梁高度和底板厚度均按照二次抛物线变化。主桥按8＃、9＃和10＃墩共3个“T”构对称悬浇施工，8＃、9＃和10＃墩墩高分别为52．5 m、62 m、60 m，除0号梁段采用搭设托架浇注完成外，其余梁段采用挂篮悬浇。边跨采用搭设支架现浇，全桥合龙顺序为先边跨、后中跨。南庄特大桥整体布置见图2。

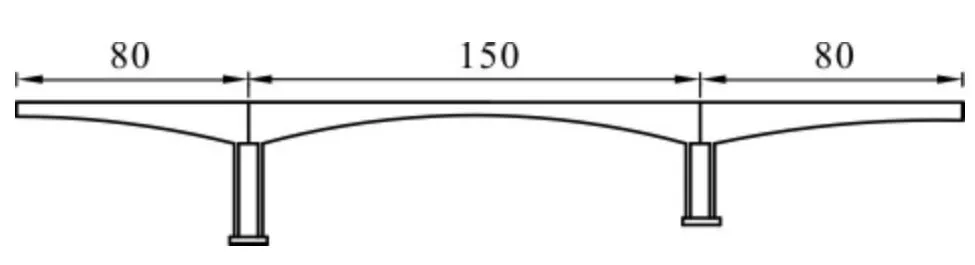
图1 贺坪峡大桥（单位：m）

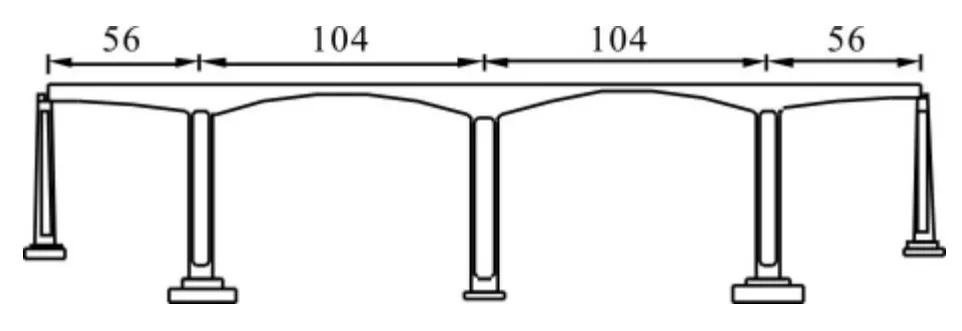
图2 南庄特大桥（单位：m）

2 有限元模型

高速公路贺坪峡大桥和高速铁路南庄特大桥均采用有限元软件Midas／Civil建模，主要包括桥墩、主梁、荷载、边界条件和施工阶段几部分。贺坪峡大桥全桥共划分116个施工阶段，共建立单元144个，节点175个，有限元模型示意图如图3所示。南庄特大桥全桥共划分94个施工阶段，共建立单元174个，节点206个，有限元模型示意图如图4所示。

图3 贺坪峡大桥全桥梁单元模型示意图

图4 南庄特大桥全桥梁单元模型示意图

3 收缩徐变对成桥预拱度的影响

在施工控制中，线形控制是非常重要的工作内容之一。这里讨论徐变效应对成桥预拱度影响是指从桥梁竣工进入运营阶段开始，直到混凝土徐变效应基本稳定为止徐变对桥梁挠度的影响。文献［2］中提到由于徐变效应持续时间较长，一般认为30 a后徐变影响基本停止，因此取成桥半年、成桥1 a、成桥3 a、成桥10 a、成桥20 a和成桥30 a进行分析，符号规定：正号表示上挠，负号表示下挠。图5所示为收缩徐变对高速公路贺坪峡大桥成桥预拱度的挠度曲线；图6所示收缩徐变对高速铁路南庄特大桥成桥预拱度的挠度曲线。

图5 不考虑收缩徐变和考虑收缩徐变贺坪峡桥成桥各个阶段挠度值（单位：mm）

图中的数据是在假设其它影响因素不变的情况下计算出来的。由数据可以看出，在不考虑收缩徐变和考虑收缩徐变两种工况下，桥梁的挠度有非常大的差异。

对于高速公路贺坪峡大桥，不考虑收缩徐变，梁体最大下挠25．1 mm；考虑收缩徐变，在成桥30 a后，梁体最大下挠达56．22 mm，增幅达到123．98%。在考虑收缩徐变的情况下，半年、1 a、3 a、10 a、20 a和30 a内梁体最大下挠值分别为45．51 mm、45．98 mm、47．12 mm、50．43 mm、53．83 mm、56．22 mm；在这5个时间段内，挠度增幅最大分别为1．03%、2．47%、7．02%、6．74%、4．43%，说明随着时间的推移，挠度增长速率逐渐增大，在3～10 a间增长速率达到最大，之后梁体挠度仍然增加，但是增长速率在逐年减少。在不考虑收缩徐变时，左右边跨有下挠现象，但考虑收缩徐变之后，一开始出现略微上挠，而后下挠。如果不考虑收缩徐变，在成桥30 a内梁体挠度变化很小。

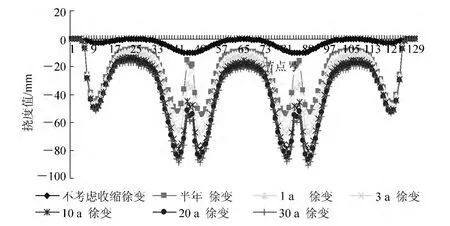
图6 不考虑收缩徐变和考虑收缩徐变南庄特大桥成桥各个阶段挠度值（单位：mm）

对于高速铁路南庄特大桥，不考虑收缩徐变，梁体最大下挠10．45 mm；考虑收缩徐变，在成桥30 a后，梁体最大下挠达90．78 mm，增幅达到768．7%。在考虑收缩徐变的情况下，半年、1 a、3 a、10 a、20 a和30 a内梁体最大下挠值分别为54．71 mm、58．97 mm、68．26 mm、79．60 mm、85．24 mm、90．78 mm；在这5个时间段内，挠度增幅最大分别为7．78%、15．75%、16．61%、7．08%、6．49%，说明随着时间的推移，挠度增长速率逐渐增大，也是在3～10 a间增长速率达到最大值，之后梁体挠度仍然增加，但是增长速率逐年减少。

就上述分析的数据来看，混凝土收缩徐变对于梁体成桥预拱度的影响非常大，所占比例很高，所以，对于混凝土收缩徐变引起的梁体挠度变化要引起足够的重视。从各个时间段内的梁体挠度增幅大小来看，成桥3～10 a间是收缩徐变对桥梁挠度影响最大的时间段，也就是梁体挠度变形最大的时间段。成桥30 a后，铁路连续刚构南庄特大桥的挠度变化明显比公路桥贺坪峡大桥大，再加上铁路对线路的平顺性要求极高，因此在施工过程中，对于铁路桥梁的预拱度设置更要严格、准确。

4 成桥后箱梁上下缘应力与梁体挠度的影响关系

桥梁结构在施工过程中以及在成桥状态下的受力变化情况对梁体结构的水平位移、梁体裂缝产生以及跨中挠度等都有重要影响。梁体结构应力的控制不像线形控制那样易于发现，若应力控制不力，考虑不周将会对结构造成危害，严重者将使结构发生破坏［3－4］。表1所列为贺坪峡大桥和南庄特大桥在成桥之后的各个时间段内梁体上下缘应力的变化情况。

表1 成桥各个时间段跨中上下缘应力和应力差情况 MPa

从表1中可以看出，在成桥之后的各个时间段内，箱梁上缘所受的压应力逐渐增大，下缘所受的压应力逐渐减少，导致上下缘应力差逐渐增大，而应力差的变化和梁体挠度变化有密切关联。

对于贺坪峡大桥而言，从成桥半年到30 a间，上缘应力变化幅度大小为0．28 MPa，下缘应力变化幅度大小为1．1 MPa，而上下缘应力差值在这6个时间点内的5个时间段内增幅分别为34．00%、43．28%、52．08%、17．17%、9．94%，与贺坪峡成桥后的挠度变化规律相同，上下缘之间的应力差值随时间变化逐年增大，在成桥后的3～10 a间达到最大，之后虽然也在增加，但速率降低。

对于南庄特大桥，从成桥半年到30 a间，上缘应力变化幅度大小为1．01 MPa，下缘应力变化幅度大小为0．47 MPa，而上下缘应力差值在这6 个时间点内的5 个时间段内增幅分别为25．00%、43．66%、55．69%、33．32%、17．07%，与南庄特大桥成桥后的挠度变化规律相同，上下缘之间的应力差值随时间变化逐年增大，在成桥后的3～10 a间达到最大，之后虽然也在增加，但速率降低。

在应力差值增幅最大的3～10 a间，相应的梁体挠度变化也是增幅最大的。通过以上分析还可以进一步看出，在两座不同类型的连续刚构桥中，箱梁底板的压应力在逐年减少，这也意味着底板拉应力在增加，而底板拉应力的增加势必会加剧底板裂缝的产生，而底板裂缝的产生又加剧跨中挠度的增加，所以，箱梁上下缘应力差值与梁体挠度变化有关，上下缘应力差值的增加会导致箱梁挠度的增大，因此，设计时应充分考虑上下缘应力差对梁体后期挠度的影响，必要时应加以控制［5］。

5 结论

连续刚构桥的跨中下挠是目前都在讨论的一个话题，其受到多方面的共同作用，本文仅考虑成桥之后，混凝土收缩徐变以及箱梁梁体上下缘应力差对梁体结构挠度的影响关系。之所以出现这种现象，主要是因为收缩徐变引起的梁体变形导致预应力钢绞线的松弛，最终梁体表现为跨中下挠。得出主要结论如下：

（1）混凝土收缩徐变对于连续刚构桥的挠度影响非常大，所占比例极高。成桥之后的3～10 a间是梁体跨中下挠增幅最快的时期。考虑到混凝土收缩徐变的重要性，不仅在理论分析上应继续深入研究，而且在模型模拟预拱度方面也要更加细化、准确，确保桥梁在施工过程中和成桥之后的梁体受力、线形情况更加合理、准确。

（2）连续刚构桥箱梁跨中上缘压应力随时间推移不断增大，下缘压应力随时间推移不断减少，导致上下缘应力差不断增大，这与梁体跨中下挠有直接的关系。若在设计方面加强对应力差的考虑和控制，对于减少跨中下挠有很好作用。

［1］朱宇峰，王解军．大跨径连续刚构桥施工控制中的混凝土徐变分析［J］．公路工程，2008，33（4）：14－17．

［2］龙永章，李伟．混凝土徐变在刚构桥预拱度设置中的应用［J］．公路与汽运，2009（4）：181－182．

［3］马保林，李子青．高墩大跨连续刚构桥［M］．北京：人民交通出版社，2001．

［4］王培金．大跨连续刚构桥长期挠度分析［D］．哈尔滨：哈尔滨工业大学，2005．

［5］张世辉．大跨预应力混凝土连续刚构桥跨中持续下挠原因分析及施工控制实践［D］．成都：西南交通大学，2007．