盾构隧道开挖对既有管线及地表的影响分析

马 林

（山西省交通科学研究院 黄土地区公路建设与养护技术交通行业重点实验室，山西 太原 030006）

0 引言

盾构法施工是目前地铁区间隧道施工广泛采用的技术之一。我国因地铁施工造成地面沉陷、周边建筑物损害、隧道涌水、城市生命线工程损害等事故时有发生，由此造成的经济损失和社会影响相当严重。其中盾构施工直接引起的地层和地表沉降是目前关注的焦点［1］。对于此类问题的研究目前主要有经验公式、随机介质理论方法、弹塑性与黏弹塑性理论解析法、数值计算方法等［2］，其中数值计算法因其能够模拟土层的变异情况、盾构管片结构－围岩共同承载特性、盾构施工工艺参数、壁后注浆参数等优点而被广泛采用［3］。

西安地铁某黄土区间盾构隧道下穿地下管线。由于黄土特有的湿陷性和结构性［4－5］和大量的地下管线，给施工带来了巨大困难［6－7］。鉴于此，采用有限差分软件FLAC3D，对此区间的盾构法施工进行了数值计算，考虑了既有管线对盾构法施工的影响，研究结果对类似工程施工提供参考。

1 工程概况

西安地铁玉洒区间始于玉祥门车站，止于洒金桥车站，区间隧道位于莲湖路正下方，区间隧道穿越西安城墙玉祥门及护城河，区间地势较平坦。该段区间隧道采用盾构法施工，隧道拱顶最大埋深17．2 m，水位线埋深为5 m。地层从上到下依次为素填土、新黄土（湿陷）、饱和黄土、新黄土（饱和）、古土壤、老黄土、分支黏土、粉土、粉质黏土、粉土、中砂、粉质黏土，埋深分别为2．5 m、6．0m、7．0m、11．4 m、15 m、17 m、21．4 m、22．4 m、24．9 m、25．6 m、28．9 m、35．0m。隧道上方有一根埋深为1．8 m 的JSDN400的铸铁管，隧道主要位于粉质黏土层。

2 数值模拟

2．1 模拟方法

地铁隧道开挖时引起的周围地层沉降是影响管线沉降的直接原因。国内外众多学者提出了隧道地表纵向沉降槽的预估经验公式［8－9］，但该经验公式不适于计算地下某一深度处地下管线的沉降，且对管隧平行时地下管线受盾构施工的影响少有研究。

前人在对土舱压力［10－11］进行研究时，均采用一均布荷载直接作用在掌子面，这与实际不太相符。盾构隧道开挖一般采用土压平衡式盾构机，其原理是盾构施加外力平衡掌子面土压力，而掌子面土压力是呈梯形分布。故采用均布荷载模拟易使开挖面前方地表隆起，后方地表沉降增大，显然是不合理的。本文在隧道开挖后及时进行衬砌安装，并对开挖面土体施加梯形支护压力（采用grad命令模拟梯形斜边，其中S0＝191．110 4kPa，gz＝9 587）。为模拟给水管线与周围土体间的摩擦作用，管线采用壳单元，并施加接触面。隧道开挖长度取为80 m，模型地表面为自由边界，其余为位移边界，侧面限制水平移动，底部为固定边界，限制水平移动和垂直移动。如图1所示。

图1 计算模型

2．2 基本假定

为了简化问题，分析问题的主要规律，计算中假定如下：

（1）地下管线为等直径、等壁厚，由于管道变形很小，管线材料本构关系可按线弹性考虑。

（2）管线按刚性接口考虑，铸铁管和混凝土管每5 m 处设置一长度为0．5 m 的接口，接口处的刚度采用强度折减法予以考虑；钢管为等刚度考虑，不设接口。

（3）假定土体为弹塑性材料，满足摩尔－库伦强度准则。地层参数见表1，每层按均匀分布考虑。

（4）地下管线位于隧道轴线的正上方，与隧道平行，此位置受施工影响最大。

（5）计算模型中，坐标原点取为隧道中心位置处，X 轴与管线轴线正交，Y 轴为隧道轴向，Z 轴为竖直方向。

2．3 计算模型及计算参数

计算模型的隧道内径为5．4 m，衬砌厚0．6m，等代层内径为6．3 m，隧道中心埋深20 m，管线外径0．4 m，壁厚0．1 m，模型长、宽、高分别为80 m、120 m、35 m，共163 200个单元，172 304个节点。计算各土体为摩尔库伦材料，管片及注浆体为弹性材料，其中注浆体用等代层［10］模拟。管道采用衬砌单元模拟，如图2所示，各部分参数选取见表1。

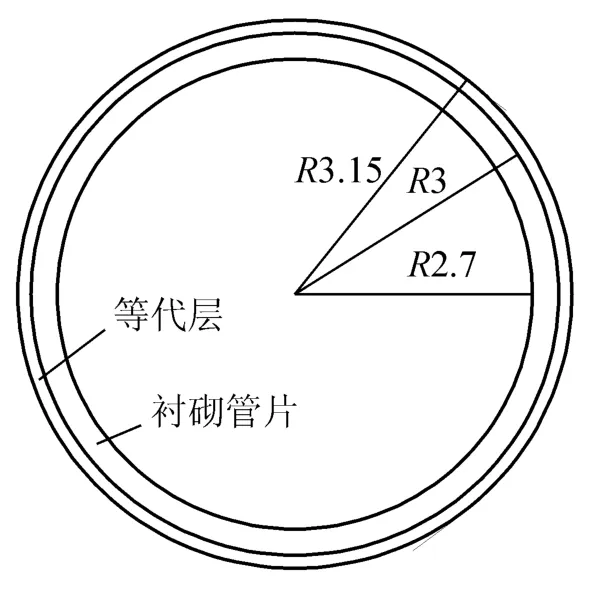
图2 衬砌管片及等代层示意图

表1 地层及支护的物理力学参数

3 隧道开挖对管线及地表的影响分析

影响地下管线沉降变形的主要因素包括管道材料、管道直径、管道埋深等，下面分别就这3方面对地铁盾构施工引起的管线沉降变形及地表变形进行分析。

3．1 不同管材对管线及地表沉降的影响

分析了给排水工程中常用材质（铸铁管、钢管、混凝土管）对管线沉降的影响，结果如图3所示，其中等直径（d ＝400mm）的3种管线计算参数见表2。

表2 管道材料计算参数

由图3可看出：3种材质管线在地铁隧道开挖过程中沉降变化规律基本一致，开挖面后方管线沉降先略微增大（距开挖掌子面大约18 m 的位置管线的沉降达到最大），而后急剧减小；在开挖面前方，管线的变形一直减小，最终趋于稳定。弹性模量变化对管线沉降的改变并不显著。同时，3种管线的最大沉降量分别为20．63 mm、20．61 mm、20．60 mm，管线的不均匀沉降允许值一般为30 mm，可见上述3种管线均处于安全状态。对管线存在时地铁隧道开挖对地表的影响进行分析，结果如图4所示。

图3 不同材质管线的沉降曲线

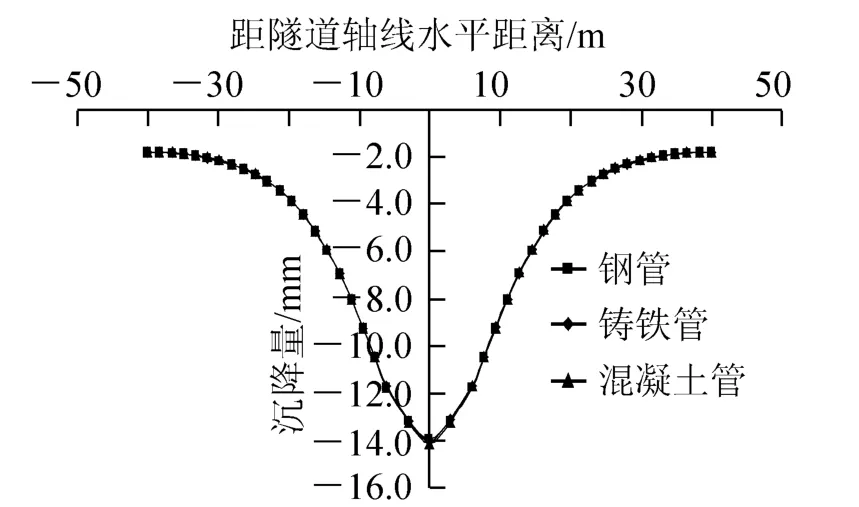
图4 不同材质管线作用下地表沉降曲线

由图4不难发现，地表沉降规律基本符合Peck沉降曲线，即高斯分布规律：中间大，两头小。3种材质的管线对地表沉降变形的影响基本一致，略微呈现出增大的趋势，3种材质管线作用下地表的最大沉降分别为13．91 mm、14．02 mm、14．14 mm，说明地铁隧道开挖时地下管线对地表的沉降变形有一定的支撑作用，管线的刚度越大，这种支撑作用越明显。

图3和图4没有出现明显区别是因为模拟的管道尺寸太小，相对整个模型是一个小窟窿，故对不同材质反应不明显，表现出地表变形和管线变形量差别不大。

3．2 不同管径对管线及地表沉降的影响

以铸铁管为对象，考察了管道直径分别为0．4 m、1 m、1．6 m 时的管线沉降变化规律。隧道纵向管线的沉降变形规律如图5所示。

图5表明，不同管径下管线沉降规律基本一致，在隧道出口端有所差异，表现为随管径增大沉降增大，原因是不同管径下小管径管线与周围土体完整性耦合较好，使得它与土体共同作用的能力较强，表现为地表沉降较大。因此在施工时要特别注意大管径管线的沉降，避免其因沉降过大发生破坏。

同时，分析了在此种工况下地表沉降变形规律，如图6所示。

由图6可看出，由于管径不同而使得隧道开挖引起的地表沉降略有不同，但基本规律保持一致，即靠近隧道方向区域影响较大，远离区域影响较小，在隧道正上方由开挖引起的沉降最大，3种管径下的最大沉降分别为14．32、14．50、14．67 mm，差异不大。

3．3 不同埋深对管线及地表沉降的影响

以直径为0．4 m 的铸铁管为研究对象，考察了管隧平行时地铁隧道开挖对地下管线的影响。结果如图7所示。

图5 不同管径下管线的沉降曲线

图6 不同管径下的地表沉降曲线

由图7可知，管线在不同埋深下的沉降量不同，即随埋深增加管线沉降随之增大。3种埋深下管线沉降曲线最大切线斜率分别为0．86 mm／m、1．00mm／m、1．58 mm／m。当管线埋深8 m 时，管道差异沉降段范围最长，切线斜率最大。原因是随着埋深的增大，管道上覆土压力增大，当地铁隧道开挖时此压力效果较明显，直接作用于管道，使得管道发生较大位移。考察不同埋深下隧道开挖对地表的影响。如图8所示。

图7 不同埋深下的管线沉降曲线

图8 不同埋深下地表沉降曲线

由图8中可以看出，开挖引起的地表沉降变形随埋深的增大而增大，在隧道正上方地表沉降量达到最大，最大沉降值分别为14．13、14．32、14．40 mm。

分析地铁隧道开挖对同一场地不同地层的沉降变形，如图9、图10所示。

图9 同一工况不同埋深地层沉降与隧道轴向的关系曲线

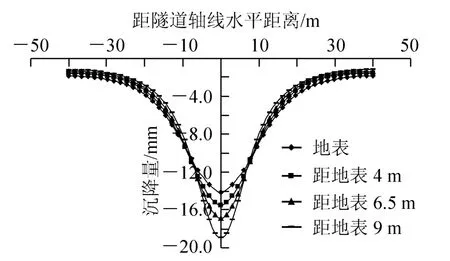
图10 同一工况不同埋深地层沉降与隧道横断面的关系曲线

从图9、图10可看出，随着埋深增大，同一工况下不同地层沉降变形增大，两者呈正比关系，原因是隧道开挖引起隧道围岩应力释放，并由围岩向4周传递，最后到达地表，在传递时逐渐递减，使得不同埋深的沉降量有所差异；从图9还可看出，在掌子面的前方，随着埋深增加地层沉降量减小，4种埋深下最大斜率分别为0．79、0．93、1．20、1．61 mm／m。图10表明，随着埋深加大沉降槽呈现出窄而高的形状，4种埋深下最大斜率分别为0．71、0．89、0．97、1．25 mm／m。

4 结论

基于西安地铁隧道玉祥门—洒金桥区间段盾构地铁隧道，应用有限差分软件FLAC3D 对盾构施工进行了数值模拟，分析了在不同管材、不同管径、不同埋深时管线及地表的沉降变形，得到了如下结论：

（1）同一场地条件下，地下管线沉降大小的影响因素主要包括管材、管径、埋深等。其中埋深的影响最为显著。

（2）地表沉降大小与管线弹性模量近似成反比关系，说明盾构施工引起管线沉降的同时管线对它上面的土体有一定的支撑作用，这种作用随管线弹性模量增大而增大，但其变化对地面沉降改变并不明显。

（3）在不同因素影响下，管线沉降曲线规律基本一致，曲线形态符合Peck曲线。

［1］刘纪峰，陶龙光，刘波．考虑盾构施工扰动土体固结的地层沉降计算［J］．辽宁工程技术大学学报：自然科学版，2009（5）：731－734．

［2］刘纪峰，刘波，陶龙光．基于弹塑性分析的浅埋盾构隧道地表沉降控制［J］．沈阳建筑大学学报：自然科学版，2009，25（1）：28－33．

［3］刘波，叶圣国，陶龙光．地铁盾构施工引起邻近基础沉降的FLAC元数值模拟［J］．煤炭科学技术，2002，30（10）：9－11．

［4］刘祖典．黄土力学与工程［M］．西安：陕西科学技术出版社，1997．

［5］高国瑞．黄土湿陷结构分类与湿陷性［J］．中国科学，1980（12）：1203－1208．

［6］张鸿儒，侯学渊，夏明耀．深开挖对周围工程设施的影响预测［J］．北方交通大学学报，1996（4）：2－3．

［7］俞建霖，赵荣欣，龚晓南．软土地基基坑开挖地表沉降量的数值研究［J］．浙江大学学报：自然科学版，1998，32（1）：95－101．

［8］王清，郭惟嘉，刘正兴．修正剑桥模型在基坑开挖分析中的应用［J］．上海交通大学学报，2001，35（4）：565－569．

［9］巩玉霞，孙志杰．隧道初期支护变形特性空间效应分析及结构尺寸优化［J］．山西交通科技，2012，3：41－44．

［10］张云．盾构法隧道的位移反分析及其工程应用［J］．南京大学学报：自然科学版，2011，37（3）：334－341．

［11］丁军霞．盾构隧道管片衬砌内力计算［J］．石家庄铁道学院学报，2004，17（2）：66－69．