航空重力测量中牛顿中心差分器对确定载体加速度的影响

周波阳 罗志才 钟 波 郑 凯 魏艳平

1 广东工业大学测绘工程系，广州市大学城外环西路100号，510006

2 武汉大学测绘学院，武汉市珞喻路129号，430079

3 武汉大学地球空间环境与大地测量教育部重点实验室，武汉市珞喻路129号，430079

4 中国石油集团工程设计有限责任公司华北分公司，任丘市建设路，062552

对机载应用来说，确定载体加速度的3种基本方法是位置求导法、相位差分法、多普勒频移法［1－4］，这3种方法都需要通过差分运算才能得出载体的加速度。牛顿中心差分器是运用最为广泛的一类差分器，其关键在于点数的选取。文献［5］分析了利用一阶牛顿中心差分器进行GPS定速的主要误差来源，认为一阶牛顿中心差分器的最佳点数应使截断误差与观测误差之和最小。这一结论是在全频谱范围内进行考虑的，适合于航空摄影测量、GPS／INS组合导航等领域。航空重力测量最终获取的是带限重力信号，需要将载体加速度从比力观测值中分离出来。由于重力信号表现为长波特性，在数据处理中需对原始观测值进行低通滤波处理，因此对航空重力测量而言，传感器原始观测值的高频部分都可认为是噪声，载体加速度只需在低频端保持足够的精度即可。考虑到这一情况，在航空重力测量的数据处理中，在全频谱范围内考虑差分器的精度可能并不合适。本文将从频谱的角度分析牛顿中心差分器的点数对航空重力测量中载体加速度的影响，并采用实测的机载GPS数据进行验证。

1 理想差分器与理想低通差分器

利用载体的位置信息通过差分方式可以计算出载体的速度和加速度。为简化问题，本文仅以垂直方向为例。由微分的定义可知：

对式（2）取极限，得：

因此，理想差分器的频率响应为：

式中，ω＝2πf为圆频率。由式（4）可知，理想差分器的频率特性在0～π内是线性增长的。和信号相比，噪声一般在高频端，而差分过程会放大噪声，特别是高频噪声。这一问题的解决办法是采用低通差分器，理想低通差分滤波器的频率响应为：

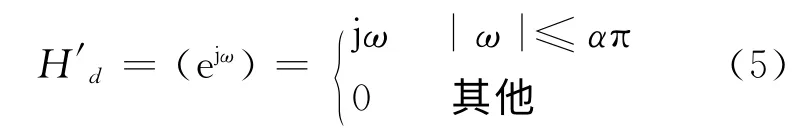
式中，απ为理想低通差分器的截止频率，频率归一化后则称α为截止频率。

2 牛顿中心差分器

理想低通差分器在物理上无法实现，人们通常采用频率响应函数H（ejω）来逼近H′d（ejω）。此时，H（ejω）一般具有以下形式：

相应的转移函数为：

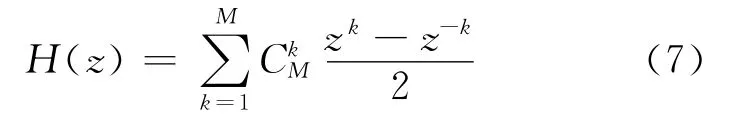
若差分器的输入为x（n），输出为y（n），则有：

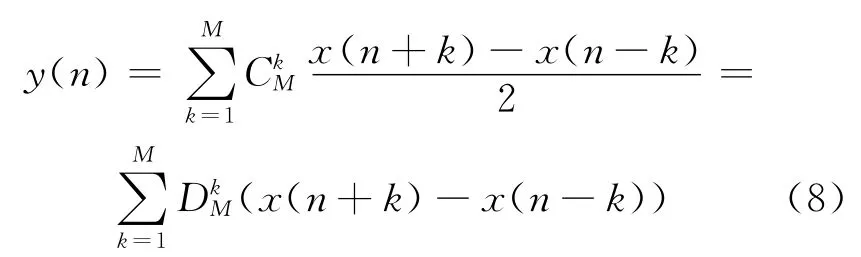
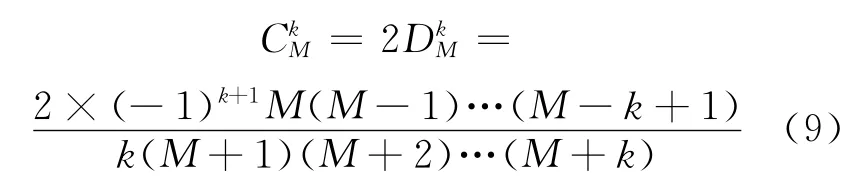
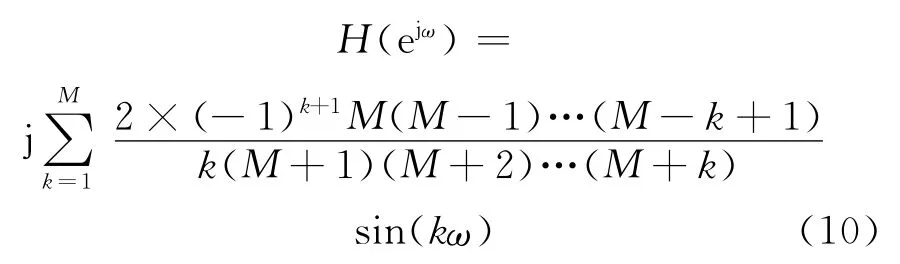
表1 一阶牛顿中心差分器的系数Tab.1 Coefficients of one－order Newton central differentiator

依据式（4）、（10），可给出理想差分器与牛顿中心差分器的幅频响应，如图1所示。从图中可以看出，牛顿中心差分器是对理想差分器的逼近，点数越多，对理想差分器的逼近效果越好，但同时差分器的低通效果在理论上也越差。文献［7］指出，低通差分器对理想差分器的逼近也可采用截止频率α来描述：απ为曲线｜H（ejω）｜与直线的交点的横坐标，如图1所示。表2给出了不同点数牛顿中心差分器的截止频率αi（i＝3，5，7，9，11），可知α3＜α5＜α7＜α9＜α11。当信号的有效频段位于低频段，且信号的截止频率α≪α3时，从理论上可以得出两条结论：1）为避免高频噪声的影响，应对差分结果进行低通滤波；2）由于不同点数的牛顿中心差分器的幅频响应在低频端完全吻合，低通滤波后不同点数的牛顿中心差分器的输出结果之间的差异应比较小。

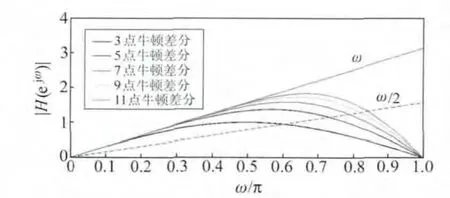
图1 理想差分器及牛顿中心差分器的幅频特性Fig.1 Magnitude－frequency characteristic of ideal differentiator and Newton central differentiators

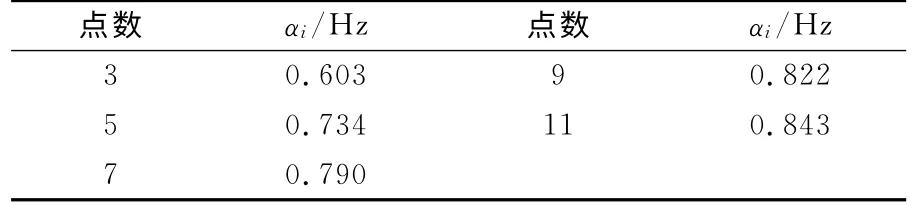
表2 一阶牛顿中心差分器的截止频率Tab.2 Cutoff frequencies of one－order Newton central differentiators

3 数值实验与分析

3.1 静态实验

选取美国某地区2个IGS跟踪站的GPS观测数据，测站编号分别为A和B，基线长度为30 km，数据采样间隔为1s，观测时间为2h。设测站A的坐标固定，将B的坐标观测值与A的固定坐标相减，可得到时间序列→ZAB，对→ZAB作二次牛顿中心差分后可得到测站B相对于测站A的加速度。由于差分过程会放大噪声，必须对差分结果作低通滤波处理。本文选用文献［9］给出的迭代高斯低通滤波器对加速度进行滤波，若载体的飞行速度为155 m／s，所需重力数据的半波长分辨率为10km，则高斯滤波器的长度为65s，对应的截止频率为α＝0.015Hz。在短时间内可认为测站B相对加速度的真值为零，因此低通滤波后所得加速度的标准差即可反映数值处理的绝对精度，表3给出了相关的统计信息。从表中可以看出，3点牛顿中心差分器输出结果的精度最优，但随着差分器点数的增加，输出加速度的精度也随之降低，同时也可认为采用牛顿中心差分器结合低通滤波器的处理方法是比较可靠的，其绝对精度优于1.8mGal。

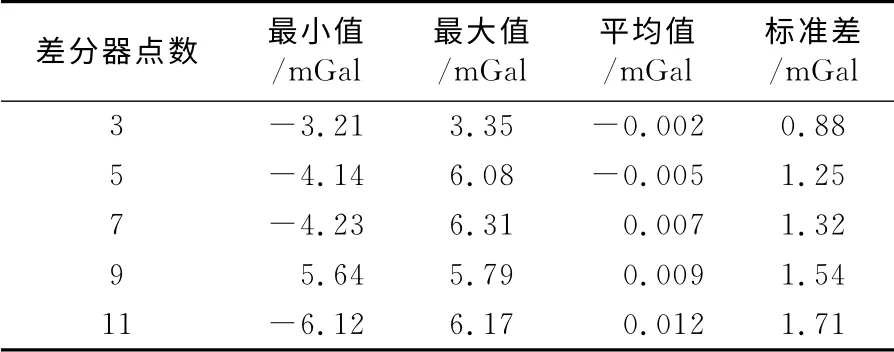
表3 基准站B 的加速度绝对误差统计信息Tab.3 Statistics of absolute acceleration error of station B

3.2 动态实验

数据来源于美国某地区的某次航空重力测量结果。测区位于路易斯安那州，航线高度约为10 668m，飞机的地面速度约为155m／s，数据采样率为1 Hz，观测时间为6.6h。采用武汉大学研制的精密单点定位软件TriP V2.0［10］解算飞机的位置信息，飞行轨迹如图2所示。航空重力测量作业的理想情况是飞机能保持直线平稳水平飞行，因此我们选取图2中的浅色部分作为测试数据，该段数据包括3 200个历元。

图2 航迹图Fig.2 Fight trajectory

对飞机z方向的位置信息作二次牛顿中心差分可得到加速度，直接差分所得加速度的频谱包含所有频段内的信息。由于观测噪声不可避免，而差分过程会对噪声进行放大，如果采用理想差分器进行数据处理，理论上在全频段内噪声的频率越高，对噪声放大得越严重。但牛顿中心差分器只是对理想差分器进行逼近，以3点牛顿中心差分为例，由表2 可知其截止频率为α3＝0.603Hz。由图3可知，在［0，α3］内，噪声频率越高放大效果越明显，甚至远远超过了信号本身的大小；而在［α3，1］范围内差分器对噪声的放大程度有所减缓，说明差分器也具有一部分低通滤波的效果。上述结果也与图1中牛顿中心差分器的幅频特性一致。

已有航空重力测量观测值的频谱分析表明，重力信号表现为长波特性，在高频端的能量几乎可以忽略不计，但图3表明，直接差分后得到的加速度的能量主要集中在高频端，因此需对直接差分得到的加速度作低通滤波处理。低通滤波器为静态实验中提及的迭代高斯低通滤波器，其对应的截止频率为α0＝0.015 Hz，易知α0≪α3。图3给出了对位置信息进行两次3点牛顿中心差分后所得加速度在低通滤波前后的PSD。从图中可以看出，低通滤波后高频噪声已得到有效消除。

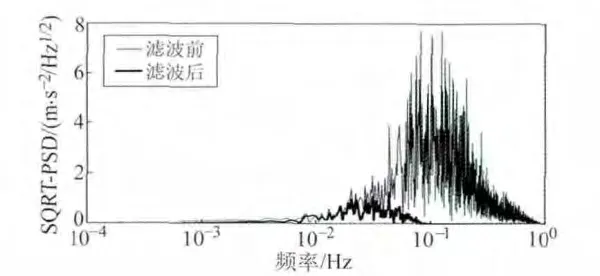
图3 低通滤波前后加速度的PSDFig.3 PSD of acceleration before and after low－pass filtering

由于没有真值作为比较，这里仅分别将5、7、9、11点牛顿中心差分器与3点牛顿中心差分器的输出结果进行比较。表4给出了低通滤波前后不同点数的牛顿中心差分器输出结果的互差统计信息，其中（3，5）表示5点牛顿中心差分器与3点牛顿中心差分器输出结果的较差，依此类推。由表4可知，低通滤波前5、7、9、11点牛顿中心差分器与3点牛顿中心差分器的输出结果较差的标准偏差在102mGal级，而滤波后较差的标准偏差已经降低至2.1mGal以内。一方面，不同点数的牛顿中心差分器输出结果之间差异较小，这是因为高斯滤波器的通带［0，α0］位于所有牛顿中心差分的通带［0，αi］（i＝3，5，7，9，11）内，且图1表明，不同点数的牛顿中心差分器的幅频响应在［0，α0］内完全一致，有差异的部分则位于高斯低通滤波器的阻带范围内；另一方面，因不同点数的牛顿中心差分器的截止频率不一样，在高频段对噪声的放大情况也不一致，同时低通滤波器不能滤除所有的高频噪声，这是不同点数的牛顿中心差分器的输出结果之间存在较差的主要原因。此外，因3点牛顿中心差分器的截止频率最小，对高频噪声的放大效果要弱于其他点数的牛顿中心差分器，同时牛顿3点中心差分器计算方便，使用简单，边界效应小。因此，在实际应用中建议使用牛顿3点中心差分器。

4 结 语

航空重力测量的有效频段位于低频端，采用牛顿中心差分器得到载体的加速度后还需对加速度作低通滤波处理。本文分析了不同点数的牛顿中心差分器的幅频响应，从理论和数值实验两方面验证了当低通滤波器的通带位于所有牛顿中心差分器的通带内时，不同点数的牛顿中心差分器所得结果经低通滤波后差异较小，建议航空重力测量数据处理时采用3点牛顿中心差分器。卫星重力测量中高低卫－卫跟踪数据差分卫星加速度的过程也可采用类似的方法进行分析。

表4 低通滤波前后不同点数的牛顿中心差分器的输出结果比较Tab.4 Result comparison of different point Newton central differentiator before and after low－pass filtering

［1］Ryan S，Lachapelle G，Gannon ME.DGPS Kinematic Carrier Phase Signal Simulation Analysis in the Velocity Domain［C］.ION，Kansas，1997

［2］Bruton A M，Gleeie G L，Schwarz K P.Differentiation for High－Precision GPS Velocity and Acceleration Determination［J］.GPS Solution，1999，2（4）：7－21

［3］肖云.利用GPS确定航空重力测量载体运动状态的理论与方法［D］.武汉：武汉测绘科技大学，2000（Xiao Yun.Research on the Theories and Methods of Determination of Moving－Base Status for Airborne Gravimetry by Using GPS［D］.Wuhan：Wuhan Technical University of Surveying and Mapping，2000）

［4］肖云，夏哲仁.利用相位率和多普勒观测值精确确定载体的加速度［J］.武汉大学学报：信息科学版，2003，28（5）：581－584（Xiao Yun，Xia Zheren.Comparison between Phase－Rate and Doppler to Determine Velocity［J］.Geomatics and Information Science of Wuhan University，2003，28（5）：581－584）

［5］王潜心，徐天河，龚佑兴.利用中心差分法进行GPS定速时最佳点数的选取［J］.武汉大学学报：信息科学版，2012，37（3）：265－268（Wang Qianxin，Xu Tianhe，Gong Youxing.Optimal Points of Using Central Differences Method for GPS Velocity Determination［J］.Geomatics and Information Science of Wuhan University，2012，37（3）：265－268）

［6］欧阳永忠.海空重力测量数据处理关键技术研究［D］.武汉：武汉大学，2013（Ouyang Yongzhong.Study on Key Technologies of Data Processing for Air－Sea Gravity Survey［D］.Wuhan：Wuhan University，2013）

［7］胡广书.数字信号处理理论、算法与实现［M］.北京：清华大学出版社，2012（Hu Guangshu.Theory，Algorithm and Implementation of Digital Signal Processing［M］.Beijing：Tsinghua University Press，2012）

［8］Cynar S J.Using Guassian Elimination for Computation of the Central Difference Coefficients［J］.Acm Signum Newsletter，1987，22（2）：12－19

［9］Hwang C，Hsiao Y S，Shih H C.Data Reduction in Scalar Airborne Gravimetry：Theory，Software and Case Study in Taiwan［J］.Computers ＆Geosciences，2006，32：1 573－1 584

［10］张小红，刘经南，Forsberg R.基于精密单点定位技术的航空测量应用实践［J］.武汉大学学报：信息科学版，2006，31（1）：19－22（Zhang Xiaohong，Liu Jingnan，Rene Forsberg.Application of Precise Point Positioning in Airborne Survey［J］.Geomatics and Information Science of Wuhan University，2006，31（1）：19－22）