一种基于大数据的前兆异常识别方法——以云南鲁甸地震为例
王秀英 张聪聪 杨德贺
1 中国地震局地壳应力研究所,北京市安宁庄路1号,100085
传统的前兆数据分析方法在实际使用中存在局限性,尤其是观测数据精度和采样率大幅提高后,这种局限性愈发突出。这是因为,采样精度和频率的提高导致数据量激增,使数据呈现的形态和变化更趋复杂多样。高频高精度数据中携带了更多低频数据所不具有的信息,同时也带来了更多干扰和影响。观测数据量的变化引发了对数据分析方法改变的需求,大数据分析方法正是基于这样一种需求应运而生。大数据分析方法目前在互联网和信息行业得到快速发展和应用,其价值和应用思想也正在被更多行业接纳和引入,将大数据的研究思路应用于科学研究也是目前的发展趋势,并在多个科学研究领域得到应用[1-2]。
地震前兆观测经过多年发展,目前已形成一个覆盖全国的数字化、网络化、智能化的观测网络体系。观测产出数据量巨大,依靠人工分析很难胜任,迫切需要引入新的研究方法。因此,本文尝试将大数据的研究思想引入前兆数据异常识别分析中。通过对2014-08-03云南鲁甸6.5级及该区域之前几个地震与多测项地震前兆数据联合应用的相关性探索,展示前兆数据大数据应用的一种思路。
1 数据及方法
1.1 研究数据
观测数据取自“十五”前兆数据库,选择鲁甸地震震中周围150km 范围内的前兆数据,共有5个台站24个测项分量数据参与计算。参与计算的测项分量如表1所示。
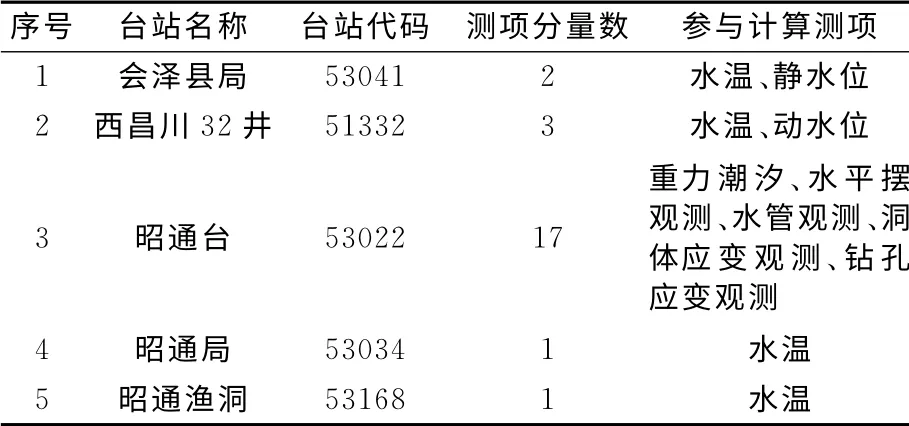
表1 台站测项分量及测项数量Tab.1 Observation item and total items of each station
自2013年以来,除本次鲁甸地震和2014-04-05地震,研究区附近没有其他较大地震。因此,先选取这些测项分量2013-01-01~2014-08-02的时均值数据作为研究对象,进行鲁甸地震的前兆数据异常识别;之后,利用该区域更长时段的数据,进行更多实例的验证。
1.2 研究方法
传统前兆数据分析方法都是针对单一测项的分析模式,异常识别靠人工观察,在识别为异常后需逐一排除干扰和影响,才能进行异常分析。针对较多测项、较长时间的观测数据进行分析时,单测项逐一分析的方式显然不可行。因此,需要利用算法自动检测并识别异常。
本文所用的异常识别算法是结合前兆观测数据特点研制的,主要检测原理是:将前兆观测数据作为一个时间序列,利用搜索算法找到时间序列的关键点,再用关键点将时间序列划分为若干子序列,以子序列的长度、高度、均值、方差作为子序列的模式,利用搜索算法选出其中明显偏离其他模式的子模式,将其作为一个异常情况。由于前兆数据是按日保存的,单纯利用一日的数据可能存在不同日数据衔接部位异常情况的丢失。因此,实际计算时可以将几个月的数据作为一个大的时间序列,然后采用向前滑动的方式,将计算窗口随时间逐步推进,最终得到检测时段的异常检测结果。本文计算中采用6个月时长作为检测窗长,3个月时长作为滑动步长。
本文所用的算法可以检测数据序列中各种异于正常的形态变化,所以各种情况引起的数据异常波动形态都会被检测出,有时可能一个序列会检测出多个异常。有关该异常检测算法的详细说明,请参阅文献[3],这里不再重复。
2 计算结果
利用异常识别算法对24个测项分量自2013年以来的时均值数据作自动扫描检测,得到异常检测结果。计算过程中会遇到个别测项个别观测日连续缺数较多的情况,这时应舍弃该日数据,然后分别对单测项异常检测和多测项联合应用的异常检测结果按自然月进行累计统计。对多个测项逐一累计统计的结果显示了很强的随机性,这里不再讨论这种情况。但当将多个测项的检测结果进行综合累计时,则表现了一些规律性。图1为按照自然月将全部测项的检测结果以异常天数、异常次数累计的统计结果。这里异常天数累积的方法为:如果某日数据中检测出异常情况,则该日累积,没有异常情况则该日不累积;异常次数的累积方法为将异常检测结果中检测的异常数据个数直接累积,如果某日有多个异常数据,则对多个异常数据进行累计。这里统计两个量的目的是便于比较,当两个量同时增加时,表明异常时间和异常数量都在增加,对应事件(如地震)的可能性增加;仅有一个量增加时,有可能是干扰因素造成的,还需更进一步分析。

图1 全部测项按自然月累计统计结果Fig.1 Statistical results of all observation items based on monthly calculation
从图1中可以看到,无论是按异常天数,还是按异常个数的累计统计结果,在2013-01~2014-03之间表现得比较随机,而2014-04 后,统计结果较之前有了明显增加,而且比较集中。2014-08,由于参加统计的只有两天的数据,在图上表现得并不明显。
实际上,由于连续多个数据缺失导致当日数据被舍弃的原因,每个月每个测项参与计算的实际数据天数会有差异。为消除这种差异,将统计结果按参与计算的天数和参与计算的测项数进行平均,所得结果称之为异常比。具体做法为:首先,计算某个测项在统计时段的异常数据点数,将统计结果除以参与统计的天数,如果没有缺数,统计天数即为统计时长,但实际中缺数现象非常普遍,通过参与计算数据天数的平均可消除每个统计时段天数不一致带来的影响。其次,汇总不同测项的累积平均异常数据,将统计结果除以参与统计的测项数。由于断数、停测、增加新测项等原因,会出现不同统计时段中参与统计的测项个数有差异的情况,通过对测项的平均可消除不同统计时段中测项数量不同带来的影响。
采用异常比这种方式主要是考虑前兆数据在实际使用中,缺数、断数、变更观测等情况比较普遍,如果仅采用有连续观测的数据,可能实际能参与计算的数据寥寥无几。大数据应用的基本思路是允许数据的混杂性,基于这种思想,计算中允许数据缺失、不连续,有数据的片段就可以参与运算。
将图1中两种统计结果消除这种影响后的统计结果如图2所示。

图2 全部测项按自然月累计的异常比统计结果Fig.2 Ratio statistical results of all items based monthly calculation
从图2可以看出,按异常比取值后的统计结果中,2014-04后异常突出的情况更加明显,尤其是2014-08,虽然只有两天的数据参与计算,利用比例关系会看到非常明显的异常情况。2014-04鲁甸地震之前本区发生一次5级以上地震,图2中2014-04的统计结果中可能包含了这次地震的影响,也可能隐含了鲁甸6.5级的影响,这里不作过多的纠结。2014-05 虽然异常水平稍有降低,但之后的6、7两月异常水平明显提高。这种情况至少具有一定的提示或警示意义。
单从图2的统计结果,似乎看到了一些规律性的东西,这种现象是巧合,还是真的具有相关性,需要进一步验证。对2013年之前更长时段的数据展开计算分析,将时间追溯至2008-01-01,由于有些台站2008年初尚未处于运行稳定期,数据质量不太好,因此只以表1中比较集中的1、3、4号台站数据作为计算对象。
另外,由于前述统计中,针对鲁甸地震只统计了地震当月2d的数据,有可能会产生局部放大的效应,所以对更长时段的数据计算及统计结果中分别利用自然月和震前1月(30d)的数据再进行计算比较。2008-01-01~2014-08-02在参与计算的几个台站周围有2次4级地震、3次5级以上地震(包含本次鲁甸地震)。表2中给出了以不同时段统计的异常比的结果,及其与地震的对应关系。

表2 地震与异常比对应关系统计Tab.2 Statistical data of earthquakes and their corresponding abnormal ratio
从表2可以看到,随着时间推移,异常比的均值和方差大致保持相似,符合平稳随机序列的特征,所以按一定时段统计得到的异常比序列可以看作一个平稳随机序列,也即长时段的异常比序列大致稳定于一定的水平,可以看作一个背景参考值,当异常比明显超过背景水平时值得关注。
表2中列出了5个地震按自然月和震前1月(30d)得到的异常比统计结果。按震前当月数据的统计结果,2014-08-03 M6.5地震的异常比超过了3倍均方差的检测标准;另2次5级以上地震的异常比也都接近2 倍均方差的检测标准;2次4级以上地震的异常比都小于均值,没有明显变化。为和其他按自然月统计标准一致,按震前1月的数据统计异常比,3次5级以上地震的异常比均超过1倍均方差标准,2次4级以上地震的异常比变化不明显。由此可见,对于研究时段的数据,当按同样统计时段检测时,5级以上地震会有比较明显的异常比变化;震级越大,异常比变化表现得越明显。另外,对于异常比有明显变化而无地震的 情 况 统 计,只 有2010-01 和2010-03 两次。
仅就研究时段得到的结果而言,异常比统计结果与地震之间具有一定的相关性,且震级越大,这种相关性表现越明显。本文仅进行了按月的统计,也可以采用半月、周等其他时段长度进行统计分析,可能会发现更好的规律。因为由经验可知,震级越大,越早出现异常,影响范围越大;震级越小,越晚出现异常,影响范围越小。不同震级的地震,异常出现的时间和影响范围,需要通过不同的条件组合,才能发现对异常反应最为突出的情况。这部分内容还需要展开更多计算和分析工作,会在后续的文章中介绍。
本文发现的这种相关性是否普遍存在,目前无法给出确定结论,只有通过对更多数据和震例数据的计算统计,才能确定这种相关性的大小。如果能确定这种相关性的存在,而且相关性较高,可以利用这种方法对数据进行日常监控,发现有持续的异常情况时发出预警,为分析预报、前兆台网提供辅助信息。有关这方面的研究应用,还需展开更多工作。
3 方法原理分析
对本文呈现的规律性及方法设计依据的初步分析如下。
单个测项由于观测中会受到各种因素影响,有些因素只影响个别测项或小区域范围的测项,有些因素则可能会影响多个测项或大区域范围内的测项。把影响个别测项的因素定义为偶然影响因素,而把同时影响较多测项的因素定义为系统影响因素。偶然影响因素包括诸如电源影响、外界干扰、人为干扰、仪器自身因素等,它们引起的数据异常,从单测项时间轴分布上来看,具有随机性。系统性影响因素包括地震、地球物理场大的变化、其他大的事件等,它们引起的数据异常,从单测项时间轴分布来看,也是随机的。这样,针对单测项数据的分析研究,对数据的精度和连续性具有极高的要求,需要精确定位和分析事件,最终的影响因素可能仍难确定。
有必要将尽可能多的测项数据引入研究中,如本文的计算方法,将尽量多测项的异常进行叠加。这是因为,偶然因素引起的异常,在数量、位置、时间等方面都是随机的,叠加后仍然是偶然的或随机的。前文中多测项累计统计数据符合平稳随机数据序列的特征,这些随机事件累加的结果会形成一定的背景水平。而系统因素引起的异常,由于同时会影响到很多测项,将它们累计时,即使存在随机异常背景,仍可以得到叠加放大,从而被突出反映。
对单个测项进行精细分析时,需要逐个事件落实。由于影响因素较多,很难进行准确原因的追溯。但当模糊化处理具体测项的具体异常事件,同时也模糊化时间尺度时,反而会使某些真正的系统性影响因素得以突出,并且很容易识别。
4 结果讨论
作为前兆数据利用大数据思想进行研究的一次尝试,本文仅使用了一种非常简单的异常检测算法。无论是地震还是其他因素导致的异常在形态上都表现得多种多样,需要不同方法的配合,才能比较全面地检测出各种情况引起的异常。所以,真正的应用,还需结合前兆数据和异常种类的特点研究更多的异常检测方法,通过多种方法的配合,可以互相印证,或者至少可以加强某种认识,对前兆数据的分析应用也是非常有益的。
需要特别指出,本文选取的台站和数据是在地震发生后,由地震的位置选取台站,而真正的数据应用,事先并不知道哪里发生地震,不可能针对具体某几个台站展开运算,而应将全部台站都作为研究对象,通过计算逐步筛选,计算筛选方法还需要大量的研究和实证工作。通过计算逐步筛选,最终确定或锁定某些台站对系统性事件的贡献最大。确定参与计算的台站需要对大量台站的大量数据进行梳理分析,与目前单测项数据分析方法截然不同,更多的工作将转向大数据计算和从海量计算结果中寻求规律的研究。由本文的分析过程可以看到,无论按哪种分类结果进行统计,都需要相当数量的测项参与,才会呈现出一定的规律性;对单个测项的统计结果,规律都不明显。而这正是大数据分析的核心思想,当更多的数据融合使用时,某些规律不是被淹没,而是更加明晰。
对单测项数据的精细分析和对更多测项综合分析的对比,使我们对舍恩伯格在《大数据时代》[2]中的论述理解得更加透彻:小数据使我们的视野局限在可以分析和确定的方面,导致对世界的整体理解可能产生偏差和错误,而大数据则可以使我们从不同角度更细致地观察和研究数据的方方面面。与局限在小数据范围相比,使用所有数据带来了更高的精确性,可以让我们看到一些以前无法发现的细节,更清楚地看到少量样本数据无法揭示的细节信息。
最后还需要指出的是,虽然在本文中,鲁甸地震及另外几个地震震前异常比累计统计结果有较为明显的增加,看似异常与地震有很好的对应关系,但由于震例数据较少,不能确定这种相关性是普适的。这种相关性是否存在,或者相关性的大小是多少,还需要对更多震例和数据展开研究,才能给出确定性结论。本文的研究过程,是将地震监测数据与大数据应用思想结合的一次尝试,具有一定的积极意义,是对传统数据分析方法的补充和完善。
[1]Hey T,Tansley S,Tolle K.The Fourth Paradigm:Data-Intensive Scientific Discovery[J].Communications in Computer &Information Science,2009,317(8):1-1
[2]Mayer-Schonberger V,Cukier K.大数据时代:生活、工作与思维的大变革[M].杭州:浙江人民出版社,2012(Mayer-Schonberger V,Cukier K.Big Data:A Revolution That Will Transform How We Live,Work,and Think[M].Hangzhou:Zhejiang People’s Publishing House,2012)
[3]张聪聪,王秀英.前兆观测异常数据检测方法研究[J].震灾防御技术,2014(9):615-621(Zhang Congcong,Wang Xiuying.Study on the Detecting Method of Abnormal Earthquake Precursor Observation Data[J].Technology for Earthquake Disaster Prevention,2014(9):615-621)

