航空重力数据向下延拓的逆泊松积分算法

2015-02-15 01:06卢雪盈柳林涛梁星辉刘金钊

大地测量与地球动力学 2015年6期

卢雪盈柳林涛梁星辉刘金钊

1 中国科学院测量与地球物理研究所，武汉市徐东大街340号，430077

2 中国科学院大学，北京市玉泉路甲19号，100049

航空重力数据向下延拓基本的解题思路是求解Poisson方程，即逆Poisson积分方法。向下延拓是一个不稳定的过程，高频噪声经向下延拓后被严重放大甚至淹没重力信号本身。为提高向下延拓的精度，许多学者提出了不同的延拓方法。Tikhonov在1977年给出了求解不适定方程的Tikhonov 正则化法，此后该方法得到广泛应用［1－9］。这些方法在一定程度上改善了向下延拓的结果，但是也都存在一些问题。例如，最小二乘配置法需要已知可靠的先验协方差模型，而重力异常的协方差模型在实际中很难精确求得；正则化方法需要选取合适的正则化参数，若参数选择不当，则会引起很大的误差；仅使用多尺度边缘约束法，对向下延拓结果的改善非常有限，它只是对现有方法的补充。

本文基于逆泊松积分进行求解，采用快速傅里叶变换和迭代法来计算重力异常。快速傅里叶变换法在计算重力场卷积积分时表现出很大的优势，并且计算速度快，原理相对较简单，特别适合处理规则格网数据，易于编程。

1 基本原理

1.1 逆泊松积分

假设函数在球外满足拉普拉斯方程ΔV＝0，则调和函数V在球面上和外部空间的关系可表示为：

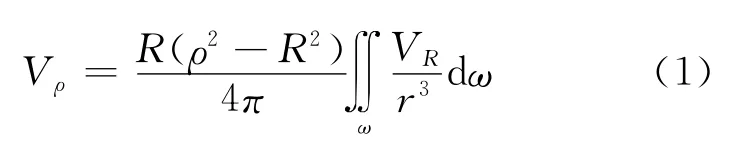
其中，Vρ和VR分别为球外和球面的调和函数，ρ为球外一点到球心的距离，R为球平均半径，r为球外点到积分元dω之间的距离，此即泊松积分。假设T为地球重力场扰动位，那么重力场的延拓在数学上可表示为大地测量第一边值问题。航空重力异常向下延拓即是求解泊松积分方程，称为逆泊松积分。

采用球面的平面近似，式（1）变换为：

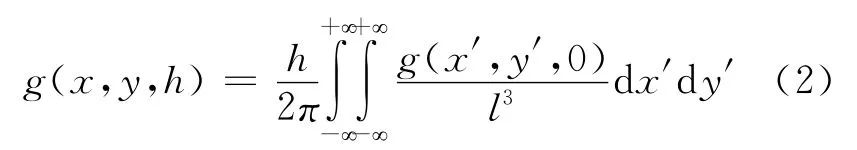
傅里叶变换具有时域卷积性质，即

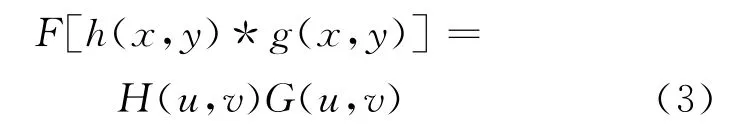
其中，F表示二维傅里叶变换算子。根据时域卷积的定义，式（2）可表达为：

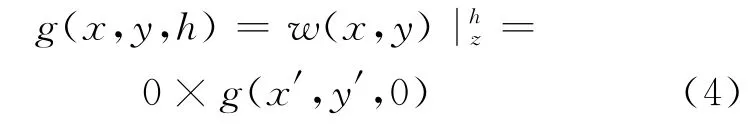
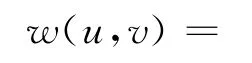
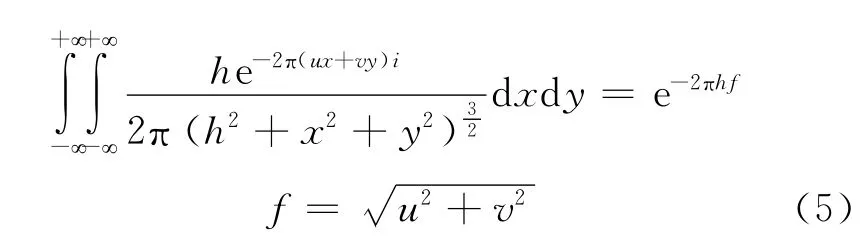
因此，式（2）在频率域表示为：

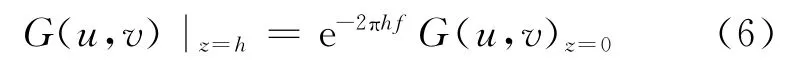
其中，G（u，v）｜z＝h和G（u，v）｜z＝0分别为h处和海平面处重力值的傅里叶变换，此为向上延拓。图1（a）给出了向上延拓的频谱特征，随着频率的增加而快速下降。

向下延拓可表示为：

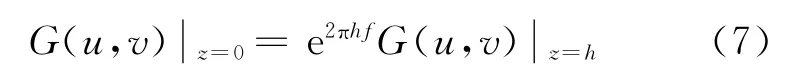
图1（b）为向下延拓的频谱特征，e2πhf这部分会放大高频噪声，很小的误差即会引起很大的反应。所以向下延拓是不稳定的，需要在算法中引入低通滤波。设计的滤波器不仅要具有良好的窄带低通特性，还要有尖锐的高频衰减性能：

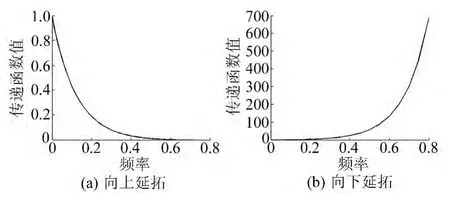
图1 延拓的一维传递函数Fig.1 The 1Dtransfer function of continuation

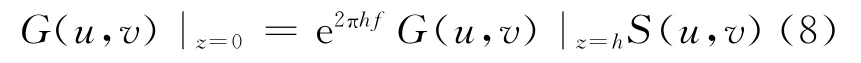
式中，S（u，v）是一个滤波器。本文选取高斯滤波器和维纳滤波器，通过实验选择最优滤波参数，并对比两种结果。

高斯函数具有旋转对称性，即滤波器在各个方向上的平滑程度是相同的，其可分离性使得较大尺寸的高斯滤波器可以有效实现。高斯滤波的传递函数如下：

其中，a为滤波参数，a越大，平滑程度就越好。采用高斯滤波向下延拓表示为：

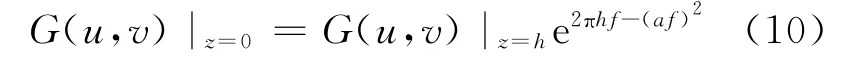
维纳滤波器（Wiener filter）是一种以最小平方为最优准则的线性滤波器。在一定的约束条件下，其输出与期望输出的差的平方达到最小。在频域，维纳滤波器可表达为［11］：

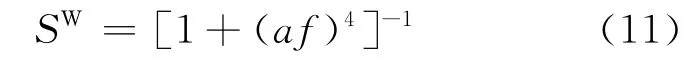
式中，a＞0为滤波参数，同样决定滤波器的平滑程度。利用维纳滤波器平滑重力异常向下延拓表示为：

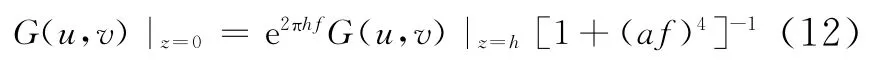
无论选用何种滤波器，a都影响向下延拓的结果。a值的选择必须经过严格的实验选出最优值，通过调节参数a，可在噪声与信号之间取得折衷。如没有外部数据检核，参数的选择可根据目标的分辨率和精度，参照EGM08模型确定。

1.2 迭代法

在实际计算中，迭代法是采用逐步趋近的方法进行计算的。已知航线高度h处的重力异常，且大地水准面外没有质量，迭代法向下延拓的步骤如下［12］：

1）将航线高度h处的重力异常Δg（x）垂直放置在h＝0，即地面的对应点上，作为初值Δg（0）；

2）将Δg（0）利用公式（6）向上延拓到h处，得到G（1）；

3）根据h处实测值和G（1）的差异，对Δg（0）进行校正，作为h＝0面的新重力异常值，然后以校正后的值再次进行向上延拓计算，Δg（n＋1）＝Δg（n）＋g（x）－G（n）；

4）重复步骤2）、3），直到h处的实测值与G（n）的差值小于设定的阈值。

2 数值计算和结果分析

为评定航空重力数据的精度以及逆泊松积分法向下延拓的精度，采用某地区2 000m 高度的航空重力异常和地面实测重力异常，格网间距为100m×100m。航空重力测量的平均飞行速度为248km／h，北－南方向共有111 条每200 m 间隔的方向线（traverse line），东－西方向共10条每2 000m 间隔的控制线（control line）。将空中重力异常向下延拓到地面，与地面已知重力异常作比较，向下延拓采用FFT 方法和迭代法，积分半径为30′。

在计算中应用了100%零填充技术以减弱循环卷积误差和边缘效应。图2表明了100%零填充的原理，除去重力格网外其余全部设置为0。

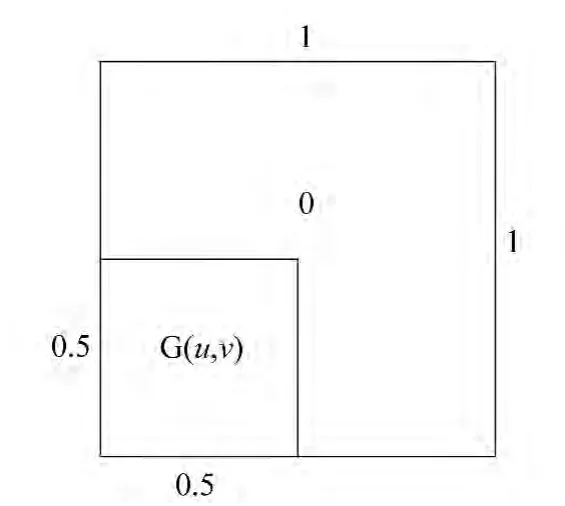
图2 延拓时采用的100%零填充原理Fig.2 The theory of zero－padding（100%）in continuation

评定航空重力数据的精度时，将地面已知重力异常按照泊松积分向上延拓到航线高度处，与空中重力异常进行比较，其差值的标准差为3.58 mGal，具体结果如表1。

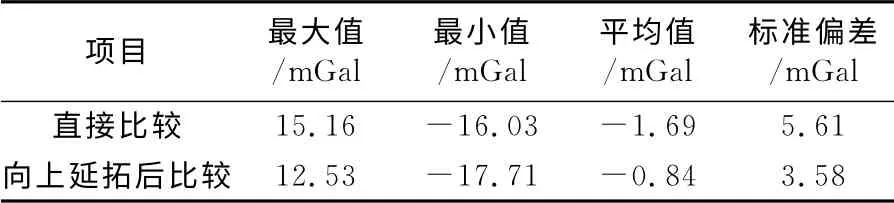
表1 空中重力异常的精度Tab.1 The accuracy of airborne gravity anomaly

选用FFT 算法向下延拓时，首先要选择滤波参数，假设a＝5，10，15，…，根据计算得到的结果选择最优值。表2为滤波参数与标准偏差的关系统计信息。

由表2知，高斯滤波和维纳滤波的参数分别为10和15时，延拓结果较好，于是在这两个参数附近取值进行计算，最后得出高斯滤波和维纳滤波的最优参数分别为10和13（表3）。

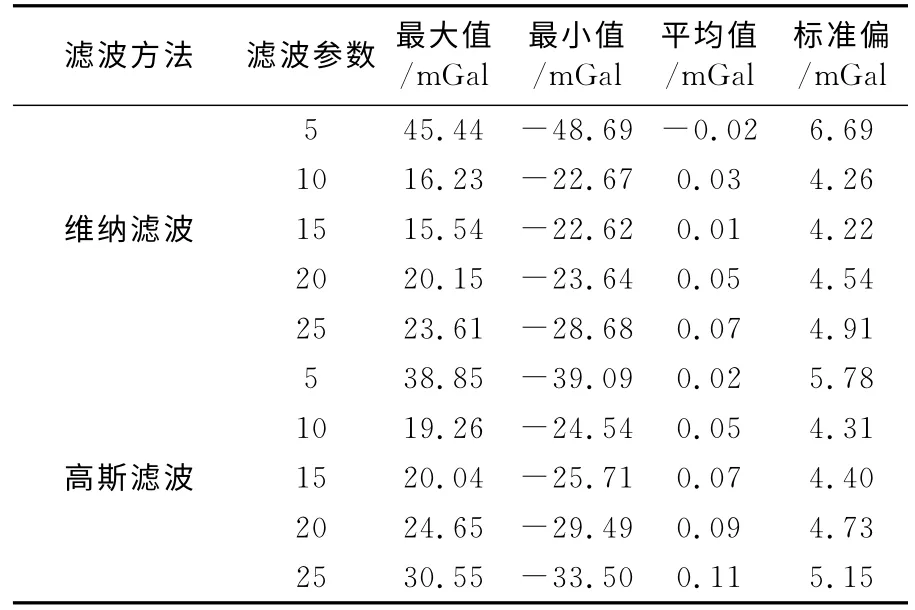
表2 重力异常向下延拓的误差统计Tab.2 Statistics of continued errors of gravity anomaly

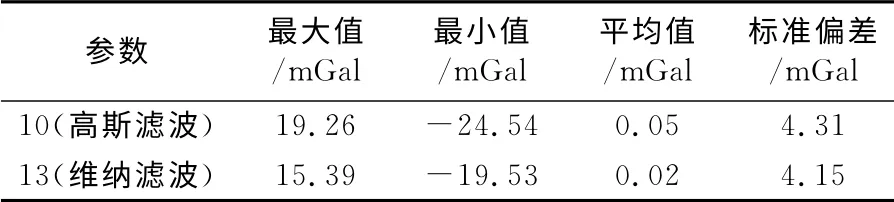
表3 最优滤波参数下重力异常向下延拓误差统计Tab.3 Statistics of continued errors of gravity anomaly in optimal filter parameters

采用迭代法进行向下延拓，当迭代次数等于50时，计算值和实测值的差值小于阈值10－2μGal。表4给出了迭代法向下延拓的结果。

表4 迭代法重力异常向下延拓统计Tab.4 Statistics of continued errors of gravity anomaly in iterative method

比较这两种结果，快速傅里叶变换算法的标准偏差为4.15 mGal，优于迭代法。图3 给出向下延拓结果与地面值差值的空间分布。

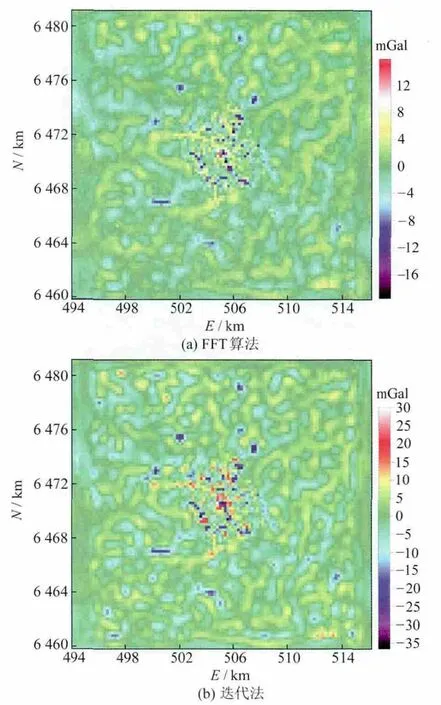
图3 两种方法向下延拓后延拓值和地面值差异的空间分布Fig.3 The spatial distribution of differences between continued value and ground value after continuation with these two methods

3 结语

采用迭代法计算时，相邻的两次迭代值具有密切关系，前一次迭代存在的误差，会影响下一次迭代的结果，反复迭代后相当于误差的累加。由于存在边界效应，每次迭代都损失一部分数据，这使得测区范围不大时，在实际应用中难以达到要求。FFT 算法运算速度快，原理简单，但是由于采用的是平面近似公式，当延拓高度较大时，精度会降低，而且忽略了远区贡献的影响引起的误差；解卷积过程有自身的缺点，e2πhf对数据中的高频噪声起放大作用，很小的一个误差即会对最后结果产生巨大的影响，因此在应用该方法时，应引入低通滤波。

本文利用实测航空重力数据，通过对FFT 算法和迭代法延拓结果进行对比和分析，评价以上两种方法的精度和可靠性。在航空重力异常精度为3.58mGal的情况下，利用FFT 算法引入低通滤波后，计算得到高斯滤波和维纳滤波最优参数分别为10 和13，相应的延拓精度为4.31 mGal和4.15 mGal；利用迭代法计算的延拓精度为4.97mGal。两种延拓结果都表明，向下延拓是一个不稳定的过程。在不考虑地形影响的前提下，FFT 算法结果较好；引入低通滤波后，在都采用最优滤波参数的情况下，维纳滤波器的性能要优于高斯滤波器。

［1］王兴涛，石磐，朱非洲.航空重力测量数据向下延拓的正则化算法及其谱分解［J］.测绘学报，2004，33（1）：33－38（Wang Xingtao，Shi Pan，Zhu Feizhou.Regularization Methods and Spectral Decomposition for the Downward Continuation of Airborne Gravity Data［J］.Acta Geodaetica et Cartographica Sinica，2004，33（1）：33－38）

［2］Tscherning C C，Rubek F，Forsberg R.Combining Airborne and Ground Gravity Using Collocation［A］／／Geodesy on the Move［M］.Springer Berlin Heidelberg，1998

［3］孙中苗.利用空中平均重力异常确定区域大地水准面［J］.郑州测绘学院学报，1999，16（4）：241－243（Sun Zhongmiao.The Determination of Regional Geoid with Aerial Mean－Gravity Anomalies［J］.Journal of the Zhengzhou Institute of Surveying and Mapping，1999，16（4）：241－243）

［4］石磐，王兴涛.利用航空重力测量和DEM 确定地面重力场［J］.测绘学报，1997，26（2）：117－121（Shi Pan，Wang Xingtao.Determination of the Terrain Surface Gravity Field Using Airborne Gravimetry and DEM［J］.Acta Geodaetica et Cartographica Sinica，1997，26（2）：117－121）

［5］宁津生，汪海洪，罗志才.基于多尺度边缘约束的重力场信号的向下延拓［J］.地球物理学报，2005，48（1）：63－68（Ning Jinsheng，Wang Haihong，Luo Zhicai.Downward Continuation of Gravity Signals Based on the Multiscale Edge Constraint［J］.Chinese Journal of Geophysics，2005，48（1）：63－68）

［6］蒋涛，李建成，党亚民，等.基于矩谐分析的区域重力场建模［J］.中国科学：地球科学，2014，44（1）：82－89（Jiang Tao，Li Jiancheng，Dang Yamin，et al.Regional Gravity Field Modeling Based on Rectangular Harmonic Analysis［J］.Science China：Earth Sciences，2014，44（1）：82－89）

［7］孙中苗，夏哲仁，王兴涛.利用航空重力确定局部大地水准面的精度分析［J］.武汉大学学报：信息科学版，2007，32（8）：692－695（Sun Zhongmiao，Xia Zheren，Wang Xingtao.Determining Accuracy of Local Geoid Determined from Airborne Gravity Data［J］.Geomatics and Information Science of Wuhan University，2007，32（8）：692－695）

［8］孙文，吴晓平，王庆宾，等.航空重力数据向下延拓的波数域迭代Tikhonov正则化方法［J］.测绘学报，2014，43（6）：566－574（Sun Wen，Wu Xiaoping，Wang Qingbin，et al.Wave Number Domain Iterative Tikhonov Regularization Method for Downward Continuation of Airborne Gravity Data［J］.Acta Geodaetica et Cartographica Sinica，2014，43（6）：566－574）

［9］Schwarz K P，Sideris M G，Forsberg R.The Use of FFT Techniques in Physical Geodesy［J］.Geophysical Journal International，1990，100（3）：485－514

［10］刘晓刚，李姗姗，吴星.卫星重力梯度数据的向下延拓［J］.大地测量与地球动力学，2011，31（1）：132－137（Liu Xiaogang，Li Shanshan，Wu Xing.Downward Continuation of Satellite Gravity Gradient Data［J］.Journal of Geodesy and Geodynamics，2011，31（1）：132－137）

［11］Forsberg R，Skourup H.Arctic Ocean Gravity，Geoid and Sea－Ice Freeboard Heights from ICESat and GRACE［J］.Geophysical Research Letters，2005，32（21）