由小波与随机采样提升重力场插值精度的策略

刘繁明 姚剑奇 荆 心

1 哈尔滨工程大学自动化学院，哈尔滨市南通大街145号，150001

随着重力测量精度的不断提高，出现了以地球重力场特征随地理位置变化的特点进行定位的重力辅助导航。相对卫星／无线电导航定位方法，重力辅助导航依靠重力测量的无源性，可保证潜器航行的隐蔽性与导航定位的可靠性［1］。重力辅助导航是基于重力基准图的有图匹配定位方法，基准图的精确性将影响匹配定位精度。

由于经济成本及其他客观原因，目前难以获得大范围、高分辨率的实测重力数据。而低分辨率数据又难以满足导航定位的要求，所以常用空间插值的方法加密实测重力数据［2－3］。因此，插值精度对重力基准图的构建较为重要。

本文首先对比研究了几种重力场插值效果较好的插值算法；而后提出以基准图小波细节信息为转移概率，由随机采样方案在基准图高频区域补充测点，从而提高插值算法精度的策略；最后进行了实验验证。

1 重力基准图插值算法

经过大量的对比实验得知，重力场插值效果较为优秀的空间插值算法有Kriging算法、改进的Shepard算法、径向基函数算法、格林函数样条算法。

1.1 Kriging算法

Kriging算法［2］是以空间区域变量理论为基础的无偏最优估计算法。该算法将观测量视为依赖空间具体位置的随机场，其中随位置变化的变量为区域化变量。并结合变异函数理论，由一定范围内空间变量的相关性对未知位置变量进行估计。

1.2 改进的Shepard算法

改进的Shepard算法［3］通过局部区域最佳二次曲面拟合数据代替已知数据，由未知点一定邻域内的拟合数据，按其与未知点的距离加权进行插值计算。具体的计算形式为：

式中，p0为未知点，pi为p0邻域内的已知测点，di为pi与p0的 距 离，Qi为 拟 合 数 据，Rw为p0的邻域半径，其选取方法可参见文献［4］。

1.3 径向基函数算法

径向基函数插值［5］为利用已知基准数据集｛pi，zi，i＝1，…，L｝，选取径向基函数φ并通过平移构造基函数系｛φ（‖p－pi‖）｝进行插值的算法。具体计算形式为：

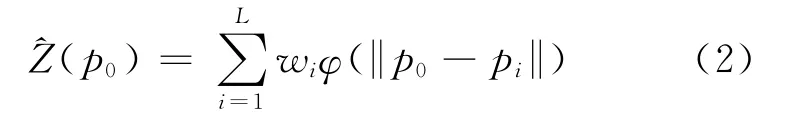
其中wi为系数，‖·‖为欧氏距离的模值。常用的基函数φ的类型有逆多重二次曲面函数、多重二次曲面函数、高斯函数及薄板样条函数，基函数中含有平滑因子c。以多重二次曲面为例，其形式为：

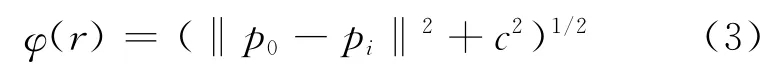
基函数及平滑因子的选取对插值精度影响较大，该影响与目标数据类型、已知基准数据分布、计算精度密切相关。经实验得知，高斯基函数的重力场插值精度较低，而文献［6］提出的优化方法可确定较优的平滑因子取值。

1.4 格林函数样条插值算法

格林函数样条插值［7］由以已知基准点为中心位置的格林函数线性叠加，形成插值曲面。基准数据或梯度信息控制各基准点处的格林函数系数。此外，引入张力以限制样条函数在基准数据间的过度摆动。具体计算形式为：

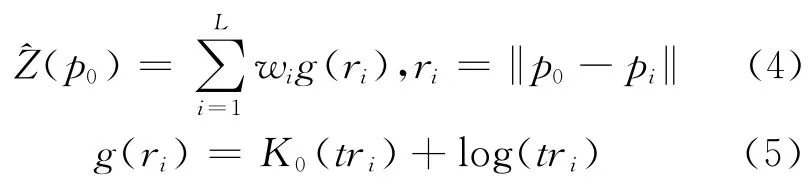
式中，wi为系数，K0为0阶的第二类修正Bessel函数，t为样条中的张力。

1.5 重力基准图插值实验

以Topex卫星重力数据（范围2°×2°，分辨率1′×1′）作为原始基准图进行插值实验，如图1所示。图1（a）、（b）的重力变化范围分别为－294～260mGal及－142～139mGal。

降采样基准图至3′×3′，由插值算法恢复至原分辨率并验证插值精度。各算法误差如表1所示（“AShepard”为改进Shepard算法，“RBF”为径向基函数算法）。Kriging采用球状变异函数模型，径向基函数算法采用多重二次曲面基函数，平滑因子为1.8。

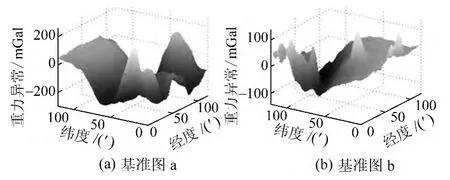
图1 重力基准图Fig.1 Gravity reference map

误差分布如图2所示（只显示误差的绝对值，以改善视觉效果）。可见不同插值算法具有相似的误差分布情况。经观察发现，插值误差较大的区域往往存在幅度较大的重力场高频信息。

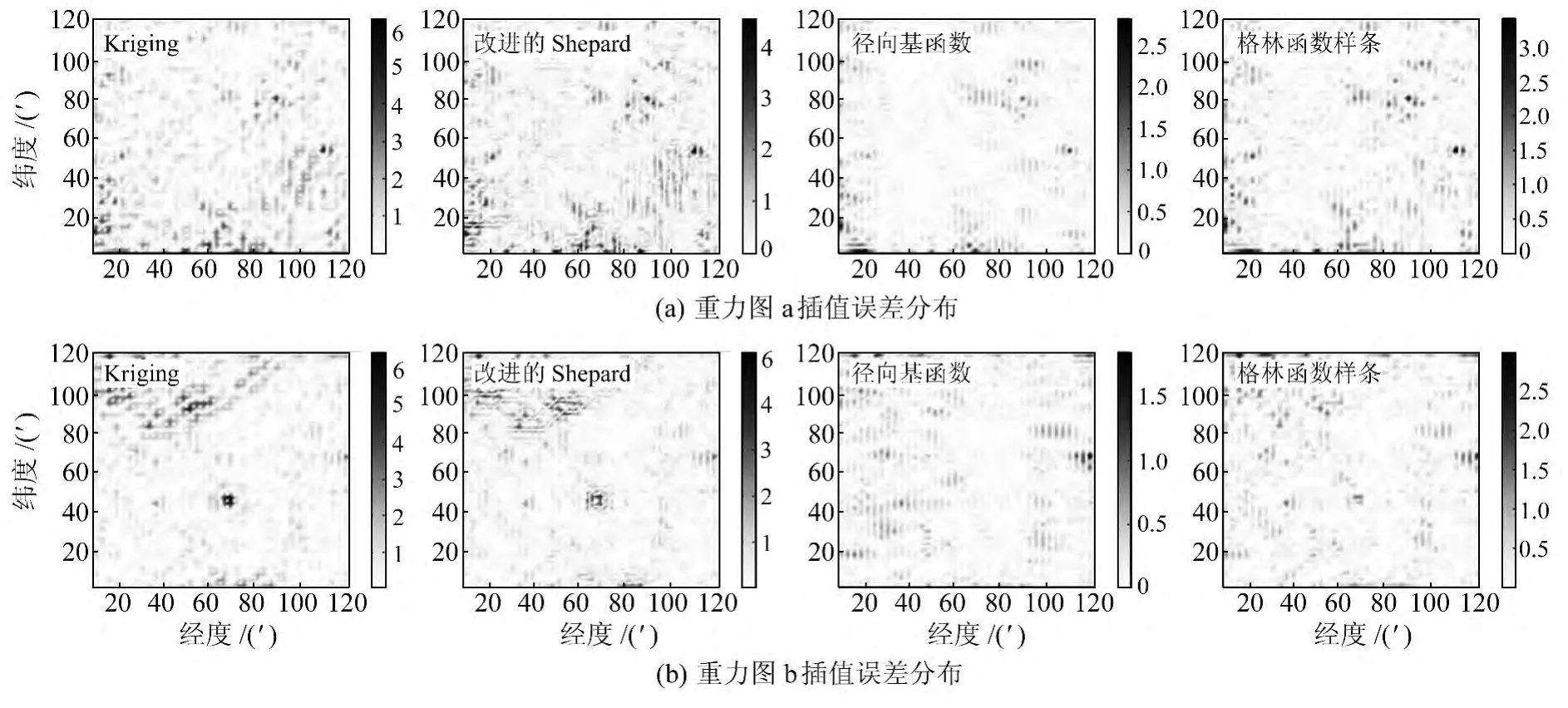
图2 插值算法误差分布Fig.2 The error distribution of interpolation algorithm

2 插值精度提升策略

2.1 插值误差分析

插值算法实质是利用已知数据估计未知位置信息的过程，所以除算法本身的特点外，已知数据的分布特征必然影响插值精度。根据Nyquist采样定理，已知数据的采样频率限制了其能反映的空间频率上限，而因实测基准图的空间分辨率有限，无法充分反映重力场细节变化，所以在高频区域产生相对较大的插值误差是难免的。

含大幅度重力场高频信息的局部区域具有弱相关性，是重力辅助导航的重点区域。由以上分析知，高频区域插值误差较大的原因为区域内的已知数据不足以刻画高频细节信息。若可在该类区域补充基准数据量（即补充测点），则可以较小的测量代价，达到有效提高插值精度的目的。

2.2 基于小波的基准图分析

小波分析具有时／频域局部分析能力，是重／磁位场数据分析的有力工具。根据相关文献［8］的研究可知，重力场的多分辨率小波细节信息可感知不同深度地质异常对应的重力异常的空间频率信息。而通过观察重力场空间频率分布发现，浅层异常产生的高频重力信息通常对应一定频段内的连续分量，若已知基准重力数据的小波细节可感知浅层异常对应频段的部分频率信息，则可确定可能含有高频重力信息的区域。

考察不同分辨率基准图小波细节信息分布，将原基准图分别降采样为2′×2′、3′×3′及4′×4′，采用重力场分析效果较好的bior3.5小波母函数［9］。因目标为确定高频区域，所以仅进行1阶小波分解。图3所示流程可将不同分辨率基准图小波细节转化为相同大小，以便比较小波细节分布情况。图3中的DHL、DLH、DHH分别为水平方向、垂直方向及对角线方向的小波细节信息。

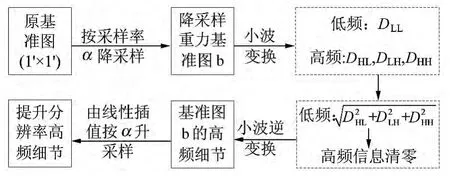
图3 小波细节转换流程Fig.3 The flow chart of wavelet detail conversion

3种分辨率小波细节如图4。2′×2′基准图小波细节清晰，与插值误差分布最相符；3′×3′的小波细节较模糊，但与误差分布基本相符；4′×4′的细节非常模糊，与误差分布相符度最差。因此，原基准数据须具有一定的密度才能探测高频区域。

2.3 基于随机采样方案的测点分布

由以上分析知，小波细节可反映基准图局部区域具有大插值误差的可能程度，则可由随机采样策略设计新增测点的分布。Metropolis采样可生成以任意分布为不变分布的马尔科夫链，则可设计如下新增测点的随机采样方案：

1）以小波细节均值为阈值，在细节图中筛选新增测点的候选位置。

2）以候选位置的小波细节为转移概率，由Metropolis采样产生测点位置。设新增测点数量为已知测点数量的20%。

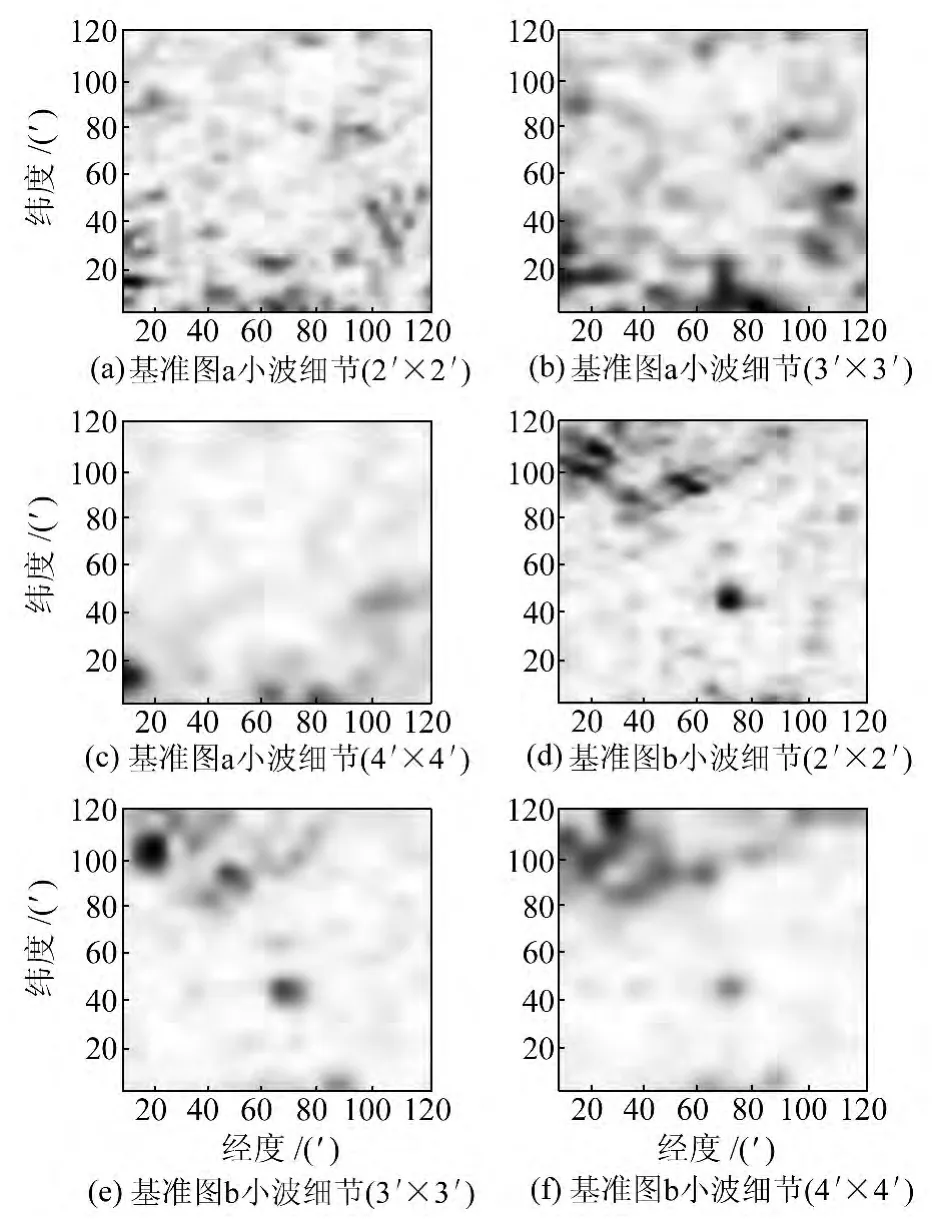
图4 基准图小波细节分布Fig.4 The wavelet detail distribution of reference map

3）为防止测点过于集中，若新测点与已知测点重合或其8邻域内已存在测点，放弃该点并继续抽样。

4）因孤立测点会降低测量工作的效率，在抽样完毕后，删除一定邻域内无其余测点的孤立点并继续抽样，直至所有测点满足以上条件。邻域半径设为15′。

基于以上策略，以3′×3′基准图的小波细节生成的测点分布如图5所示。

增加测点后的插值算法误差分布如图6，误差统计如表2。因增加测点后，各插值算法仍为无偏估计，即误差均接近0，表2中省去均值而只给出标准差。此外，设各算法原插值误差标准差为a，新增测点后的误差标准差为b，则表2中“精度提升”为（a－b）／a×100%。

图5 新增测点分布Fig.5 The distribution of incremental measurement points

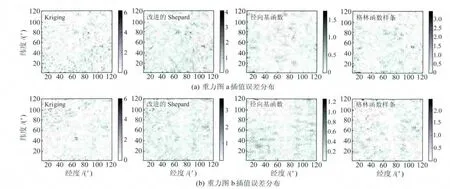
图6 增加测点的插值误差分布Fig.6 The error distribution of interpolation algorithm for measurement points increased

表2 增加测点后的插值误差统计Tab.2 Statistical data of interpolation error for measurement points increased

可见，各算法在高频区域的误差有所减弱。由统计数据知，误差的范围、标准差均有一定程度的改善，而径向基函数算法的改善程度最为显著。

2.4 对比方案

在整个基准图范围内，按均匀分布生成测点（新测点不与已知测点重叠）。设新增测点数为1 000（相当于已知测点数量的61%），该方案的插值误差统计数据如表3所示。

通过对比两种方案可知，在插值精度提升程度基本相同的情况下，在高频区域增加测点的方案所需的测点数量较少，而且误差的极值较小。

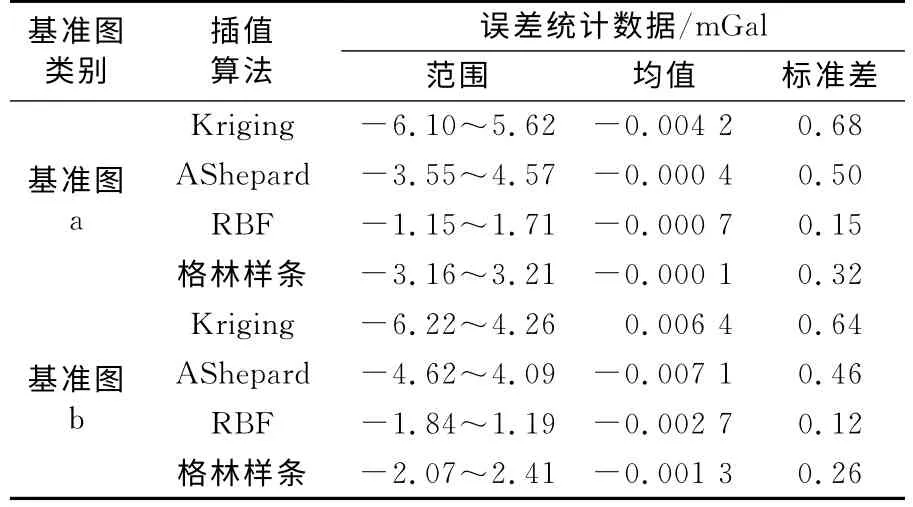
表3 新测点均匀分布的插值算法误差统计Tab.3 Statistical data of interpolation error for measurement points distributing uniformity

3 结 语

本文通过插值实验指出，插值算法在重力场高频区域往往含有较大的误差。而后利用小波分析可感知浅层地质异常产生的重力异常空间频率信息的特点，提出以基准图小波分解的细节信息为转移概率，由随机采样方法在重力场高频区域增加测点，提高对高频信息的刻画能力，从而提高插值精度的策略。插值实验表明，相对均匀分布新增测点的方案，在插值精度提升程度相同的情况下，本文策略所需的测点数较少，误差的极值较小，以较小的代价获得了较优的插值效果。

［1］Lowreys J A.Passive Navigation Using Inertial Navigation Sensors and Maps［J］.Naval Engineers Journal，1997（5）：245－251

［2］成怡，刘繁明，郝燕玲.海洋重力图加密仿真实验研究［J］.中国惯性技术学报，2007，15（2）：206－208（Cheng Yi，Liu Fanming，Hao Yanling.Simulation Experiment Research on Marine Gravity Map Interpolation［J］.Journal of Chinese Inertial Technology，2007，15（2）：206－208）

［3］吴太旗，黄谟涛，陆秀平，等.重力场匹配导航的重力图生成技术［J］.中国惯性技术学报，2007，15（4）：438－441（Wu Taiqi，Huang Motao，Lu Xiuping，et al.Gravity Map Creating Technology in Gravity Matching Navigation［J］.Journal of Chinese Inertial Technology，2007，15（4）：438－441）

［4］Renka R J.Multivariate Interpolation of Large Sets of Scattered Data［J］.ACM Transaction on Mathematical Software，1988，14（2）：139－148

［5］Wright G B.Radial Basis Function Interpolation：Numerical and Analytical Developments［D］.University of Colorado，2003

［6］Rippa S.An Algorithm for Selecting a Good Value for the Parametercin Radial Basis Function Interpolation［J］.Advances in Computational Mathematics，1999，11：193－210

［7］Wessel P.A General－Purpose Green’s Function－Based Interpolator［J］.Computer ＆ Geosciences，2009，35（6）：1 247－1 254.

［8］杨文采，施志群，侯遵泽，等.离散小波变换与重力异常多重分解［J］.地球物理学报，2001，44（4）：534－541（Yang Wencai，Shi Zhiqun，Hou Zunze，et al.Discrete Wavelet Transform for Multiple Decomposition of Gravity Anomalies［J］.Chinese Journal of Geophysics，2001，44（4）：534－541）

［9］李健，周云轩，许惠平.重力场数据处理中小波母函数的选择［J］.物探与化探，2001，25（6）：410－417（Li Jian，Zhou Yunxuan，Xu Huiping.The Selection of Wavelet Generating Functions in Data－Processing of Gravity Field［J］.Geophysical ＆Geochemical Exploration，2001，25（6）：410－416）