一种模糊趋近律转台伺服系统滑模控制器设计
唐立力,吕福起
(重庆工商大学融智学院基础课教学部,重庆 南岸 400033)
摩擦存在于所有的运动中,特别是对高性能伺服系统的影响尤为突出.对于转台伺服系统来说,摩擦是影响系统低速性能的重要因素,会造成位置跟踪出现“平顶”和速度跟踪出现“死区”现象,造成较大的稳态误差,使系统产生爬行、震荡,降低位置跟踪精度,很难用传统的控制方法达到高精度控制[1-2].目前,很多控制技术都用来对摩擦环节进行补偿.例如自适应控制、观测器技术、神经网络等[3].将滑模变结构控制技术应用到摩擦补偿的研究也很多[4-6,10,11].
本文针对具有较大非线性摩擦影响的三轴转台伺服系统,以某型转台的一轴为研究对象,提出一种补偿摩擦力矩的新方法.在常规的趋近律滑模控制中引入模糊控制,利用模糊控制器来动态调整滑模控制的趋近律参数,设计了一种补偿摩擦的模糊趋近律滑模控制器.仿真结果表明,该控制器优于常规指数趋近律滑模控制器,有效地抑制了摩擦力矩的影响,保证了系统的快速性和鲁棒性,同时还削弱了常规滑模控制产生的抖振,实现了高精度的位置跟踪.
1 带模糊趋近律滑模控制的转台伺服系统模型与摩擦模型
1.1 系统模型
考虑一个三轴转台伺服系统,转台控制系统是由3 个独立的通道组成,控制结构基本相同,任意框的模型在正常情况下可简化为线性二阶环节的系统,在低速情况下具有较强的摩擦现象,此时控制对象变为非线性.该系统采用直流电机驱动,忽略电枢电感,电流环和速度环为开环,系统结构如图1所示.

图1 模糊趋近律滑模控制的转台伺服系统结构图
对图1所示的系统,有如下的状态方程[9]:

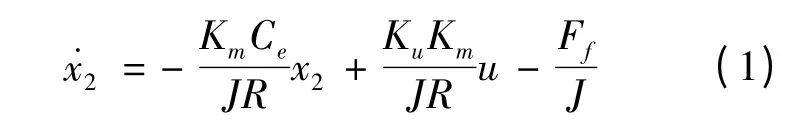
上式中,x1= θ 为转角,x2=为转速,Ku为PWM 功率放大器放大系数,Km为电机力矩系数,R 为电枢电阻,Ce为电压反馈系数,J 为负载的转动惯量,u 为控制输入.
1.2 摩擦模型[7]
针对伺服系统,目前已经提出了许多摩擦模型.本文仿真中采用较为常用的Stribeck 摩擦模型,摩擦—速度稳态关系曲线如图2所示.

图2 摩擦-速度稳态关系曲线(Stribeck 曲线)


上式中,F(t)为驱动力矩,Fm为最大静摩擦力矩,Fc为库仑摩擦力矩,kv为粘性摩擦力矩比例系数,(t)为转动角速度,α 和α1为非常小的、正的常数.
2 模糊趋近律滑模控制器的设计
2.1 滑模控制器设计
设r 为系统期望的位置跟踪轨迹,x1为系统实际输出轨迹.令e = r-x1为系统位置跟踪误差,对于二阶系统,滑模线方程s(e,t)= 0 定义为:

上式中,c 为正常数.
采用指数趋近律:

上式中:ε >0,k >0 为趋近律的参数,εsgn(s)为滑模控制项.当s →0 时,ks →0 ,但εsgn(s)却不趋于零,所以也不趋于零,系统状态将会来回地穿越滑模面而造成抖振,而且抖振的强度由ε 的大小来决定.
考虑系统摩擦力Ff的影响,由(1)式得

通过指数趋近律(6)式我们可以得到控制律为:

2.2 模糊控制器设计
由系统状态方程(1)式,当摩擦存在时,必然会引起系统状态变量的值发生变化.由于滑模面s 是关于状态变量的函数,那么摩擦的大小必然会影响到s 的值,可以通过s 的值来间接估计.这样就形成了一种新的补偿摩擦的方法.可以设计一维模糊控制器,它根据s 的绝对值大小来实时调整趋近律的参数ε,原理如图3所示.

图3 模糊控制器原理图
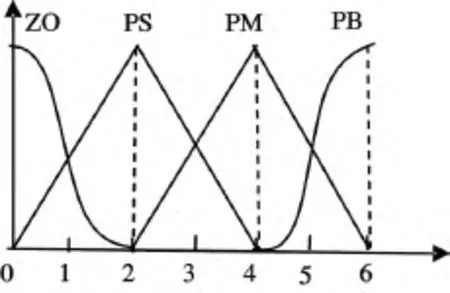
图4 输入输出模糊语言变量的隶属度函数

表1 模糊控制规则
反模糊化方法采用重心法[8].去模糊化公式如下:
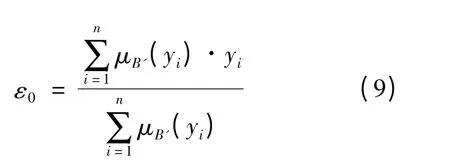
这样就可以求出最终的控制律u.
3 仿真与分析
本文以某三轴转台伺服系统作为实例[9],在Matlab7.1下进行仿真,系统模型和摩擦模型参数如下:
R =7.77 Ω,Km=6 Nm/A,Ce=1.2 V/(rad/s),J = 0.6 kgm2,Ku= 11,Fc= 15 N·m,Fm= 20 N·m,kv= 2.0 Nms/rad,α1= 1,α = 0.01.
取采样时间为1 ms,经仿真调试确定c =9.5,常规指数趋近率参数为k = 10,ε = 5,模糊指数趋近率参数为k = 10.模糊控制器参数取为:ks= 1,kε= 1.
位置指令为:r = 0.1sin(2πt)
系统初始状态:x1(0)= -0.4,x2(0)= 0 .
系统的跟踪曲线、控制量曲线和切换线s 变化曲线的对比仿真结果见图5~图10.

图5 模糊指数趋近率滑模控制位置跟踪曲线
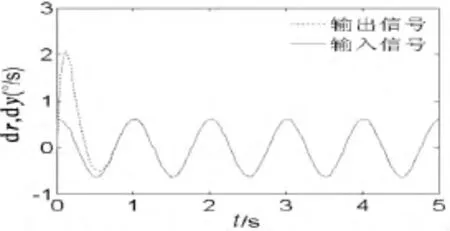
图6 模糊指数趋近率滑模控制速度跟踪曲线
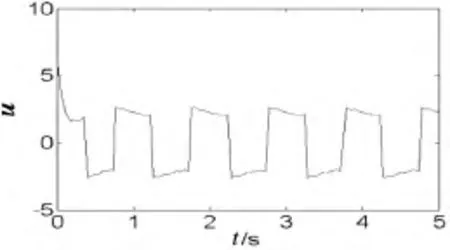
图7 模糊指数趋近率滑模控制量曲线

图8 指数趋近率滑模控制量曲线

图9 模糊指数趋近率滑模控制切换线s 变化曲线放大图
仿真结果分析:
1)从图5和图6中可以看出,模糊趋近率滑模控制的系统输出能够快速地跟踪期望值,实现了高精度的位置和速度跟踪.
2)对比图7和图8,可以看出模糊指数趋近律滑模控制量相对常规指数趋近率滑模控制量来说切换幅度明显减小,抖振明显减弱.再比较图9与图10,可以看出模糊趋近律滑模控制的滑模切换线s 上的抖振比常规指数趋近率滑模控制明显减弱.
4 结语
本文将模糊控制和滑模控制有机地结合起来,针对具有较大非线性摩擦影响的三轴转台伺服系统,提出了一种带模糊趋近律的滑模控制器设计方法.从仿真结果可以看出,该控制器优于常规指数趋近律滑模控制器,有效地抑制了摩擦,削弱了抖振,实现了高精度的位置跟踪,跟踪的快速性较好,同时保证控制系统的鲁棒性.算法简单,易于实现.
[1]刘金琨.先进PID 控制Matlab 仿真[M].北京:电子工业出版社,2004.
[2]高为炳.变结构控制的理论及设计方法[M].北京:科学出版社,1996.
[3]刘强,尔联洁,刘金琨.摩擦非线性环节的特性、建模与控制补偿综述[J].系统工程与电子技术,2002,24(11):45 -52.
[4]Sivakumar S,Farshad K.Friction Compensation via variable structure control:regulation and low2 velocity[C].In Proceedings of the 1997 IEEE International Conference on Control Applications,1997:67 -69.
[5]Liu Jinkun.Sliding mode controller design for position and speed control of flight simulator servo system with large friction[J].Systems Engineering and Electronics(China),2003,14(3):59 -62.
[6]肖颖杰.飞行仿真转台伺服系统滑模控制器设计[J].微计算机信息,2005,21(5):12 -14.
[7]Karnopp D.Computer simulation of stick -slip friction in mechanical dynamic systems[J].Journal of Dynamic Systems,Measurement and Control,1985,107:100 -103.
[8]李士勇.模糊控制、神经控制和智能控制论[M].哈尔滨:哈尔滨工业大学出版社,1998.
[9]刘金琨.滑模变结构控制Matlab 仿真[M].北京:清华大学出版社,2005.
[10]李跃磊,王武,葛瑜.飞行模拟转台伺服系统滑模控制仿真[J].机械设计与制造,2011(3):206 -208.
[11]刘晓东,吴云洁,田大鹏,等.基于干扰观测器的飞行仿真转台滑模控制器[J].上海交通大学学报,2011,45(3):393 -402.

