等价权函数为连续可变函数的抗差Kalman滤波

蔡 奇 刘 宁 戴吾蛟 杨德地

1 中南大学地球科学与信息物理学院，长沙市麓山南路932号，410083

可靠的Kalman滤波算法是基于可靠的函数模型和随机模型［1］，当系统状态模型不准确或观测误差中含有粗差时，Kalman 滤波算法性能将大为降低甚至导致滤波发散。这种情况下，一般将抗差估计与Kalman 滤波相结合，建立抗差Kalman滤波算法进行滤波估计［2］。

抗差估计的设计一般通过建立等价权函数来实现［3］。现有的等价权主要有Turkey、Huber、Hampel、IGGⅠ、IGGⅢ等［4－5］，其共同特点为分段函数，涉及分段降权临界值的选取问题，而临界值的选取一般根据误差检验的置信水平和经验来确定［6］。为克服凭经验确定统计量临界值所带来的抗差效果风险，欧吉坤［6］提出一种将抗差初值、综合抗差以及优化抗差效率结合起来的三步抗差方案，杨元喜等［7］则利用学生化残差统计量构建一种临界值可变的抗差估计等价权函数。而对于不同的抗差环境，除临界值可变外，等价权的函数形态也应不同。为此，本文从粗差检验统计量的分布规律出发，提出一种等价权函数为连续函数且函数形态可变（continuous variable，简称CV）的抗差估计方法，其抗差性能优于传统模型。

1 连续可变等价权函数设计与分析

1.1 连续可变等价权函数的设计

抗差Kalman滤波算法的关键是抗差等价权函数的设计以及定位参数、尺度参数的确定［8］。

等价权函数的函数形态应含有3个阶段——高端平缓区、低端平缓区以及介于两者之间的下降收敛区，即“反S型”曲线。据此，设计连续可变等价权函数模型：

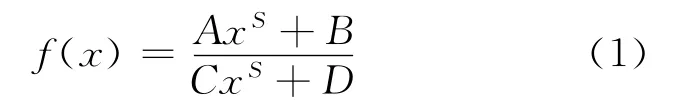
其函数形态为“反S型”，A、B、C、D为待定参数，S为形态参数。

假定该函数有3 个特征点，当x＝k0时，f（x）＝1，使函数从1 开始下降；当x＝a时，f（x）＝1／2，用来控制其收敛速度；当x＝k1时，f（x）＝0，使函数收敛为0。并且设a∝S，由此可以联立以下3个方程：

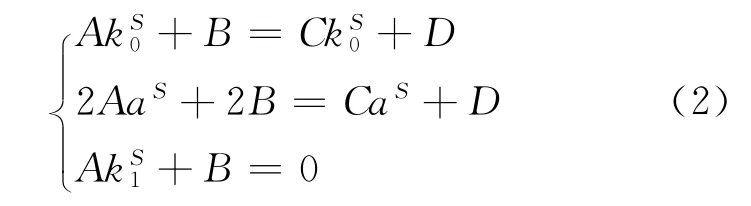
解得：

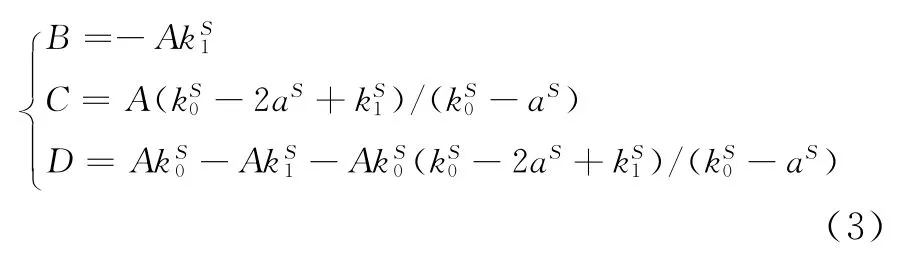
由标准正态分布的性质可知，k0＝0，k1＝∞。将k0＝0与式（3）代入式（1），得：

又当k1＝∞时，

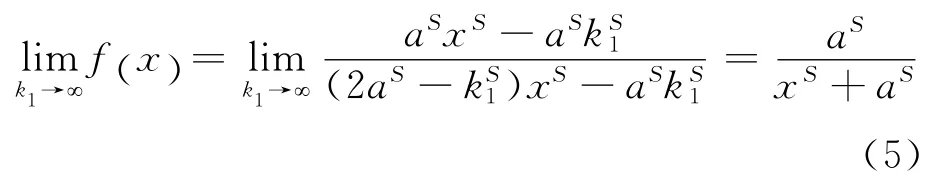
在条件一定的情况下，S视为常数，那么当x增大到一定程度时，a近似于x的线性函数，使得函数形态向右移，但同时可能会出现x增大时，f（x）函数尾部向0收敛过慢。

为解决函数尾部收敛过慢问题，现对函数进行一定的修改。假设系统的模型误差为υm，当a＞υm时，因为已经超出模型误差改正的范围，权函数应立即收敛为0，而由于上述情况的发生，有可能导致权函数并未收敛。所以，现构造f（x）k函数，通过k值来控制收敛。

由于0＜f（x）＜1，当x＞υm时，应使k＞1来控制f（x）k值收敛下降；当x＜υm时，应使0＜k＜1来控制f（x）k值不收敛。滤波过程中υm未知，在实际数据中随着υm模型误差增大，导致粗差检验统计量右移，因此抗差过程中，需要将抗差降权区域右移。由于f（x）中S形态参数越大，对应的函数形态最初高端平缓区越长，即抗差区域右移，因此υm与S应具有正比关系。不妨设υm∝S2，取：

综上所述，最终所得的函数为：

其中，a＝（x2＋S2）／（xS）。

将该函数模型应用到等价权函数中，得CV抗差方案模型：

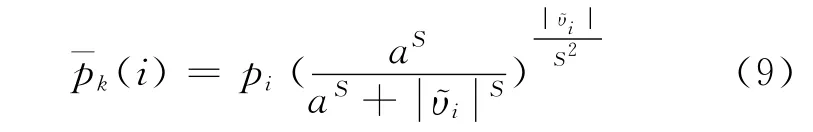
1.2 等价权函数模型分析

1）该抗差模型是根据实际情况下的标准化残差的分布以及形态系数来确定函数模型的形态，以此设定一个较好的函数形态来处理数据。通过调整函数形态系数S，可以灵活地处理不同情况下的数据。

2）从图1可知，当S＝0.8时CV 函数模型与Turkey函数模型形态近似一致。从图2可知，当S＝2时CV 函数模型与Huber函数模型形态近似一致。当0＜S＜1 时，适用于线性模型；当S＞1时，适用于具有系统误差的非线性模型。随着S的增大，CV函数模型可以由Turkey 到Huber转换。假设S是时间t的函数，可以根据不同时刻的具体环境动态改变CV 函数形态，从而达到更好的抗差效果。

图1 抗差方案权因子函数模型（CV形态参数S＝0.8）Fig.1 The model plot of robust weight function（S＝0.8）

图2 抗差方案权因子函数模型（CV形态参数S＝2）Fig.2 The model plot of robust weight function（S＝2）

2 实验分析

2.1 模拟实验数据

为比较分析基于连续可变等价权函数的抗差Kalman滤波算法的滤波处理效果，先利用两组模拟数据，采用以下5种方案进行对比分析：IGGⅢ法、IGGⅠ法、Turkey法、Huber法、连续可变等价权函数法。

1）第一组模拟数据。首先利用式（10）非线性运动模型计算得到5 000个观测真值序列，然后在所有观测值上加入中误差为5的随机误差，并随机选择50个观测值加入大粗差，作为观测值：

2）第二组模拟数据。利用式（11）模型计算得到5 000个观测真值序列，然后在所有观测值上加入中误差为0.5的随机误差，并随机选择50个观测值加入大粗差，作为观测值：

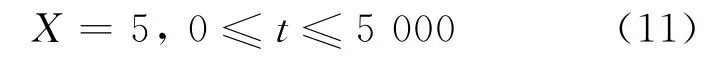
2.2 真实实验数据

这里引入五强溪大坝引张线变形观测数据——22个控制点的2 978个时刻的时序数据。考虑到数据处理的时间效率，选择1～5号控制点200个时刻的数据进行分析。在实际处理中，选择一段数据比较平稳的时段，人为在50、100、150时刻加入粗差污染。

2.3 实验成果与分析

标准Kalman与CV 滤波残差比较见图3，非线性模拟数据处理（CV 形态参数为5）见图4，线性模拟数据处理（CV 形态参数为0.5）见图5。

1）由图3可知，标准Kalman滤波抗差效果较差，当观测信息存在较大粗差时，标准Kalman滤波值不可靠。

2）从表1可知，对于非线性数据，滤波时存在系统误差，由图4以及不同抗差方法RMS比较可以看出，在较小系统误差情况下，不宜将观测值的权迅速降低。IGGⅠ、Huber和CV（S＝5）在处理非线性数据上具有较好的效果，而Turkey 的处理效果不佳。从图4（c）和表2可知，由于Turkey 整体降权导致过抗差现象，因此抗差滤波发散。

3）对于线性数据，根据图5可知，Turkey和CV（S＝0.5）数据处理效果更好。由于模型建立准确，因此整体降权下的滤波效果更好。

4）本文提出的抗差方法可以根据实际，灵活地对函数形态进行调整，从而更好地适用于Turkey和Huber的滤波环境。而且不用过多地尝试阈值的设置，在抗差滤波使用上较为方便，抗差滤波的结果稳健性较好。

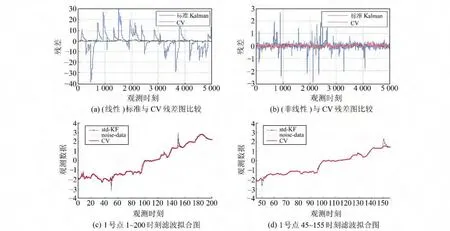
图3 标准Kalman与CV 滤波残差比较Fig.3 The residual plot of Kalman filtering ＆CV filtering

图4 非线性模拟数据处理（CV 形态参数为5）Fig.4 Non－linear analog data calculation（S＝5）

图5 线性模拟数据处理（CV 形态参数为0.5）Fig.5 Linera analog data calculation（S＝0.5）

表1 非线性数据与线性数据时各类模型之间的RMS值Tab.1 The RMS of linear and non－linear data for different models

表2 真实数据时各个滤波方案RMS值比较Tab.2 The comparison for RMS of different schemes under true data

3 结 语

针对目前抗差估计在Kalman滤波中的不同算法，总结了各个抗差方案的适用范围，并通过分析抗差处理中存在的问题，提出一种基于连续可变等价权函数的抗差方案——CV 法。通过两组模拟实验和真实数据处理表明：

1）Turkey适用于线性数据，Huber适用于非线性数 据，而IGG Ⅰ、IGG Ⅲ和CV 法 抗 差 适 用范围更广；

2）从灵活度上来看，CV 法可以根据系统实际情况及时调整函数形态，从而进行较为可靠的抗差滤波。

［1］付梦印，邓志红，张继伟.动态Kalman滤波理论及其在导航系统中的应用［M］.北京：科学出版社，2003（Fu Mengyin，Deng Zhihong，Zhang Jiwei.Thesis on Dynamic Kalman Filtering and Its Application in Navigation System［M］.Beijing：Science Press，2003）

［2］宋迎春.动态定位中的卡尔曼滤波研究［D］.长沙：中南大学，2006（Song Yingchun.Research on Kalman Filtering in Dynamic Positioning［D］.Changsha：Central South University，2006）

［3］李德仁，袁修孝.误差处理与可靠性理论［M］.武汉：武汉大学出版社，2002（Li Deren，Yuan Xiuxiao.Error Processing and Reliability Theory［M］.Wuhan：Wuhan University Press，2002）

［4］杨元喜.抗差估计理论及其应用［M］.北京：测绘出版社，1993（Yang Yuanxi.Robust Estimation Principle and Its Application［M］.Beijing：Surveying and Mapping Press，1993）

［5］周江文.经典误差理论与抗差估计［J］.测绘学报，1989，18（2）：116－118（Zhou Jiangwen.Classical Error Theory and Robust Estimation［J］.Acta Geodaetica et Cartographica Sinica，1989，18（2）：116－118）

［6］欧吉坤.一种三步抗差方案的设计［J］.测绘学报，1996，25（3）：173－179（Ou Jikun.A Design on Three－Step Robust Estimation Project［J］.Acta Geodaetica et Cartographica Sinica，1996，25（3）：173－179）

［7］杨元喜，吴富梅.临界值可变的抗差估计等价权函数［J］.测绘科学技术 学报，2006，23（5）：317－320（Yang Yuanxi，Wu Fumei.Robust Estimation Equivalent Weight Function of Variable Critical Value［J］.Journal of Geomatics Science and Technology，2006，23（5）：317－320）

［8］杨玲，沈云中，楼立志.基于中位参数初值的等价权抗差估计方法［J］.测绘学报，2011，40（1）：28－32（Yang Ling，Shen Yunzhong，Lou Lizhi.Method of Equivalent Weight Robust Estimation Based on the Initial Value of Neutral Position Parameters［J］.Acta Geodaetica et Cartographica Sinica，2011，40（1）：28－32）