高阶电离层改正对PPP对流层估计的影响

徐韶光 熊永良 王德军 陈伟伟

1 西南交通大学地球科学与环境工程学院，成都市高新区西部园区，611756

电离层延迟是电磁波信号在通过电离层时引起的偏差。在精密单点定位（PPP）中，通常通过消电离层组合来消除一阶电离层以提高参数的解算精度。由于一阶电离层延迟在总电离层延迟中占99%以上，而相位消电离层观测量中的二阶电离层一般不超过2cm，目前大多数用户在数据处理时未加入该项改正［1－3］。但在mm级定位中，若处于低纬度区域或电离层异常时，则必须考虑二阶项甚至三阶项。不少学者研究了二阶电离层对定位精度的影响，但高阶电离层改正对对流层估计的影响却未见报道［4－7］。本文在探讨二阶、三阶电离层计算方法的基础上，重点研究高阶电离层对PPP对流层估计的影响。

1 顾及高阶电离层影响的对流层估计模型

顾及高阶电离层影响的PPP模型如下：

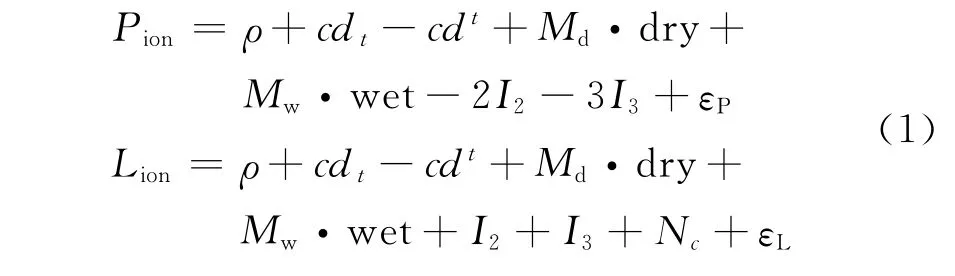
其中，Pion、Lion分别为伪距和相位消一阶电离层观测量，包括各项误差改正［8］；ρ为卫星至测站的空间几何距离；dt为接收机钟差；dt为卫星钟差；c为光速；Md、Mw分别为干延迟和湿延迟投影函数，dry、wet分别为对流层天顶干延迟和湿延迟；I2为二阶电离层延迟；I3为三阶电离层延迟；Nc为组合模糊度；εP、εL为未模型化的伪距和相位噪声。干延迟的近似值可以通过GPT 模型求取［9］，则待估参数为：

其中，Nm为第m颗卫星对应的组合模糊度。

将式（1）线性化，得：

其中，

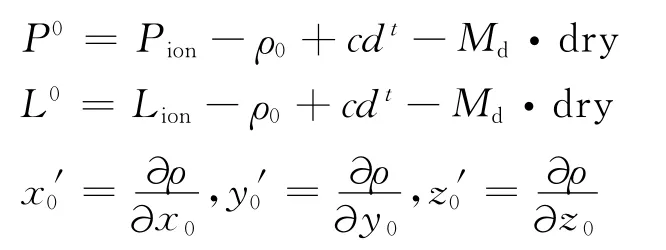
若投影函数用三角函数近似表示，则：

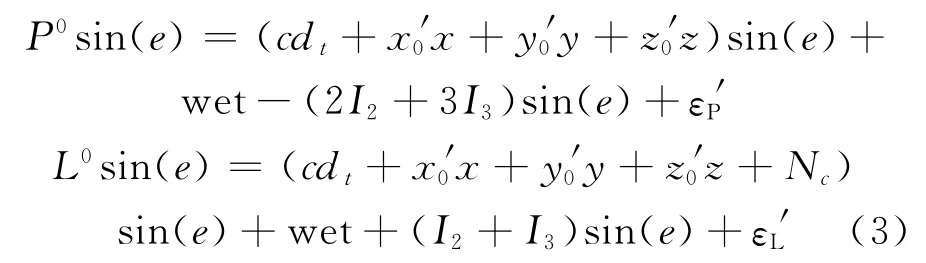
由式（3）可知，二阶、三阶电离层对伪距和相位方程中湿延迟的影响与卫星高度角的正弦函数密切相关，其影响因子如图1所示。

由图1可知，高阶电离层对伪距的影响远大于对相位的影响，但通常在精密单点定位过程中伪距观测量赋予的权比相位观测量赋予的权小100倍，导致对最终结果起主导作用的仍为相位观测量。如在天顶方向，高阶电离层延迟值达1cm，则将有可能给该方向的对流层引入1cm 的误差。改正该项误差，可以提高对流层延迟的解算精度。

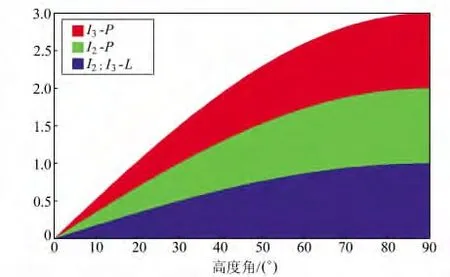
图1 高阶电离层对天顶对流层延迟的影响Fig.1 High－order ionospheres’effect on zenith tropospheric delay

2 高阶电离层延迟的计算

二阶电离层计算公式如下［1，3－4］：

式中，f1、f2分别为载波信号L1与L2对应的频率，s可以采用下式计算：

其中，B为电离层穿刺点处的地磁场强度，单位为T；θ0为地磁场向量与卫星信号发射方向的夹角；STEC为信号传播路径上的电子总量。

穿刺点的位置计算一般采用单层模型，如图2所示。式（5）中B可采用国际地磁参考场模型来计算，其分量计算式如下［10］：

其中，r、θ、λ分别为地心距离、地心余纬度、大地经度，a＝6 712.2km；gmn、hmn分别为高斯系数；Pmn（cosθ）是与地心余纬度有关的标准正交缔合勒让德多项式。只需提供r、θ、λ三个参数，便可通过IGRF模型获取任意一点的地磁场分量。式（6）得到的是北、东、径向的地磁场矢量，通过旋转矩阵R0可以得到空间直角坐标系里面的分量，以便于求取θ0：

式中，a为磁场在笛卡尔坐标系中的矢量，b为信号发射方向的矢量。

STEC采用Hernandez－Pajares方法计算［3］：

其中，DCBrP1－P2为接收机硬件延迟；DCBSP1－P2为卫星硬件延迟，可以从IGS分析中心获取，也可以自行编写软件计算。

由式（5）知，二阶电离层的大小主要取决于穿刺点的磁场强度，以及磁场方向与信号发射方向的夹角和传播路径方向的总电子含量。其精度与地磁场模型有关，Dipole 模型的准确度约为75%，而IGRF模型则精度更高［3，11］。

图2 电离层穿刺点示意图Fig.2 Schematic diagram of ionospheric pierce point

三阶电离层的计算可采用下式［11］：

将上式进行简化，得：

由式（11）知，三阶电离层完全取决于传播路径上的电子总量。由于该项误差的值恒为正，如果卫星分布测站四周，水平方向误差将抵消一部分，它将会更多地影响PPP 垂向参数的估计精度。

3 数据处理及分析

3.1 顾及高阶电离层影响的精密轨道产品计算

为分析高阶电离层对对流层延迟估计的影响，首先对2013－05－01的80 个测站观测量进行二阶电离层改正，或同时进行二阶和三阶电离层改正，然后利用改正后的观测量进行定轨，同时求取相应的卫星钟差［12］。该工作可由GAMIT 软件完成。由于电离层延迟途径为卫星信号传送至接收机的方向，该方向与卫星至地心方向的夹角最大约14°，而cos（14°）约为0.96，故高阶电离层改正对轨道的径向精度影响最大。此外，卫星钟差直接反映视线方向的距离误差，因此高阶电离层改正也有益于提高该项参数估计的精度。经解算，加入与未加入二阶电离层改正的轨道径向相差最大约2cm，沿轨方向和垂直轨道面方向最大相差约1cm，卫星钟差相差不到1.5cm。这与Elsobeiey的结果相比偏小［6］，可能与软件的系统偏差有关，另外时间也有影响。而三阶电离层对轨道任何方向的影响均不超过1cm，对卫星钟差的影响也不超过1cm。

3.2 顾及二阶电离层影响的对流层估计

利用经过二阶电离层改正后的轨道和钟差产品作为起算数据，根据式（1）估算地面测站的对流层。该步骤由自行编写的精密单点定位程序完成。选取的测试测站不在估算轨道产品的测站之内。其中，TWTF 站的30颗卫星对应的二阶电离层如图3所示，加入与未加入二阶电离层改正估计得到的对流层差值如图4所示。

图3 TWTF站的二阶电离层延迟Fig.3 Second order ionospheric delay of TWTF site

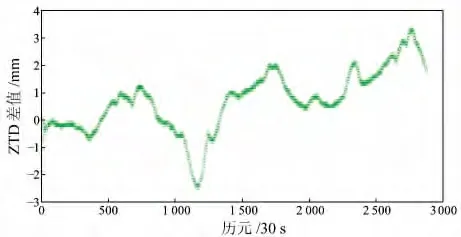
图4 加入二阶电离层改正后的对流层与初始对流层的差值Fig.4 Tropospheric delay difference between after correcting I2and original

由图3可知，对于TWTF 站，二阶电离层引起的消一阶电离层相位观测量误差达1.5cm，如采用单频观测量则其影响扩大1.4倍或2.9倍。TWTF测站的纬度为24.95°，经度为121.165°，属于偏低纬度地区。该测站的二阶电离层相对较大，通常情况下二阶电离层在中纬度地区达到5～10mm 较常见。由图4可见，二阶电离层对对流层的影响达几mm，TWTF 站中最大影响超过3mm，转换成可降水量约为0.5mm。由式（5）可知，二阶电离层的影响与磁场强度有很大关系，而地磁强度在低纬度地区相对较大，导致二阶电离层延迟较大。如要获取精密的对流层延迟，则必须进行该项改正。

3.3 顾及三阶电离层影响的对流层延迟估计

以MKEA 测站为例，该站的最大二阶电离层延迟不超过13 mm，该站当天观测到的32 颗卫星的三阶电离层延迟如图5所示。图6则是该站分别加入二阶与三阶电离层以及仅加入二阶电离层与未加任何高阶电离层所估计的对流层的差值序列。

图5 MKEA 测站的三阶电离延迟Fig.5 Third order ionospheric delay of MKEA site

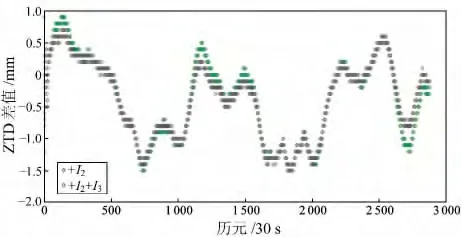
图6 加入高阶电离层改正后的对流层与初始对流层的差值Fig.6 Tropospheric delay difference between after correcting high－order ionosphere and the original

由图5知，MKEA 测站三阶电离层的值达到5mm，但从图6看，三阶电离层对对流层的影响甚小，不超过0.3mm。MKEA 测站的纬度约为19.8°，经度为－155.456°。通过与其他测站的计算数据比较，该站的三阶电离层值相对较大。

需要注意的是，高阶电离层的大小与时间有关。根据目前的电离层活跃周期，可大致判断2013年电离层属于中度偏高活跃期［13］。在电离层峰值期，要想获取1mm 精度的对流层延迟，则需要同时进行二阶与三阶电离层改正。

4 结 语

1）二阶电离层在低纬度地区对观测量的影响可超过1cm，对对流层的影响可达3～4mm。若需获取1mm 精度的对流层延迟，则中、低纬度地区的测站应加入二阶电离层改正。

2）三阶电离层的量级相对较小，一般不会超过5 mm，对对流层的影响一般不会超过0.5 mm，可忽略不计。

致谢：感谢IGS提供跟踪站数据，感谢MIT授权使用GAMIT 以及Bob King耐心指导。

［1］Bassiri S，Hajj G.High－order Ionosphere Effects on the Global Positioning System Observables and Means of Modeling Term［J］.Manuscr Geod，1993，18：280－289

［2］郭均祥，雷源汉.高阶电离层效应对GPS 观测量的影响［C］.中国地球物理学会第11届学术会议，1995（Guo Junxiang，Lei Yuanhan.Higher Order Ionosphere Effect on GPS Observations［C］.The 11th Annual Meeting of the Chinese Geophysical Society，1995）

［3］Hernandez－Pajares M，Juan J M，Sanz J，et al.Second－order Ionosphere Term in GPS：Implementation and Impact on Geodetic Estimates［J］.J Geophys Res，2007，112（B08417）：1－16

［4］Kedar S，Hajj A，Wilson B D，et al.The Effect of the Second Order GPS Ionospheric Correction on Receiver Positions［J］.Geophys Res Lett，2003，30（16）：1 829

［5］Fritsche M，Dietrich R，Knofel C，et al.Impact of Higherorder Ionospheric Terms on GPS Estimates［J］.Geophys Res Lett，2005，32（L23311）：1－5

［6］章红平，吕海霞，李敏，等.电离层延迟二阶项改正模型化及其对精密定位影响［C］.第二届中国卫星导航学术年会，2011（Zhang Hongping，Lv Haixia，Li Min，et al.Modeling Second－order Ionospheric Effects and Corrections on GNSS Precise Positioning［C］.The 2th Annual Meeting of China Satellite Navigation Conference，2011）

［7］Elsobeiey M，El－Rabbany A.On Modelling of Second－Order Ionospheric Delay for GPS Precise Point Positioning［J］.The Journal of Navigation，2012，65：59－72

［8］Jan K.A Guide to Using International GNSS Service Products［Z］.IGS，2009

［9］Bohm J，Heinkelmann R，Schuh H.Short：A Global Model of Pressure and Temperature for Geodetic Applications［J］.Journal of Geodesy，2007，81：679－683

［10］Finlay C C.International Geomagnetic Reference Field：the Eleventh Generation Geophysical Journal International［J］.Geophysical Journal International，2010，183：1 216－1 230

［11］Marques H A，Monico J F G，Aquino M.RINEX＿HO：Second－and Third－order Ionospheric Corrections for RINEX Observation Files［J］.GPS Solutions，2011，15（3）：305－314

［12］Herring T A，King R W，McClusky S C.GAMIT Reference［Z］.MIT，2009

［13］Petrovay K.Solar Cycle Prediction［J］.Living Rev，Solar phys，2010，7（6）