基于SSA的GPS坐标序列去噪及季节信号提取

罗 勇 匡翠林 卢辰龙 曾凡河

1 中南大学地球科学与信息物理学院，长沙市麓山南路932号，410083

2 郑州市市政工程勘测设计研究院，郑州市民生路1号，450052

SSA是在Karhumen－Loeve分解理论基础上逐渐发展起来的，是对一维时间序列进行周期震荡的主成分分析方法，它从时间序列的动力重构出发，并与经验正交函数相关，不受正弦波假定的约束，从含噪的数据中尽可能多地提取可靠信息，将具有显著震荡的分量提取出来，并且选择其中若干有意义的分量进行重建，从而降低噪声［1－2］。本文基于模拟数据和IGS跟踪站BJFS站的实测数据，采用SSA、db10小波和EMD 方法进行对比分析，并通过精度统计指标比较3种方法在GPS坐标序列去噪和周期信号提取方面的优劣势。

1 SSA基本原理

SSA 的分析对象是经过中心化后的一维时间序列x1，x2，x3.....xN，对其进行滞后排列，选择合适的窗口大小M（M＜N／2），建立一个滞后矩阵［3］：

求出滞后矩阵Y的协方差矩阵C（它是一个类似于Toeplizt的矩阵，其对角线上的元素都相同）：

再求出C的特征值λ1≥λ2≥…≥λM≥0和特征向量。式就是时间序列的奇异谱，对其奇异值进行的运算称为奇异谱分析。λk对应的特征向量Ek称为时间经验正交函数T－EOF（temporal empirical orthogonal function）［4］。之后计算滞后序列Y在Ek上的投影：

式中，0≤i≤N－M，1≤j≤M，aik为Ekj所反映的时间演变权重，称为时间主成分，记为TPC。

SSA 最重要的功能是重建（reconstruction component，RC）［5］。由第k个时间主成分（TEOF）和时间主分量（TPC）重建的成分记为：

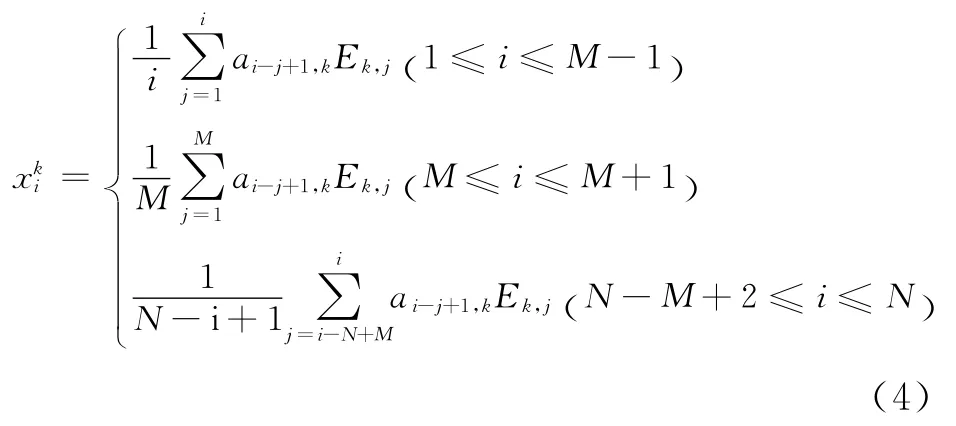
根据SSA 原理，当原序列中存在一个周期振荡成分时，SSA 得到一对接近相等的特征值，对应的一对TEOF 正交，一对TPC 正交。为不失一般性，设这对特征成分序号为k和k＋1。满足上述条件的第k和k＋1的RC 之和是一个周期振荡成分。然而，用离散的有限长度序列作SSA时，即使是周期信号，也得不到λk＝λk＋1，而TEOF及TPC之间总是正交的。所以，实际应用中依据这些条件识别周期振荡成分较困难。因此，Vautard［3］和Ghil［6］根据谱性质提出了相应的补充判据。由于SSA 具有稳定识别周期信号的优点，SSA 及MSSA 在趋势提取与周期信号提取中有着广泛的应用［6－7］，在大地测量领域也有初步的应用［8－9］。

2 比较分析方法与精度评定指标

2.1 小波和EMD 基本原理

对于任何的信号或者可积函数f（t），它的连续小波变换为［10］：

Wf（x，y）是基本小波函数，x和y分别是伸缩和平移因子，ψ＊（t）是ψ（t）的共轭函数。y确定小波的中心位置，x确定小波的时域广度。因此，在分析时间序列时，只要恰当地选取小波函数，便能得到较好的频域和时域局部性［11］。

经验模式分解（EMD）是对一组时间序列进行平稳化处理，将原始信号分解成一组从高频到低频的基本信号，每个信号都代表了一个本征式的分量，即固有模态函数（intrinsic mode function，IMF），IMF要满足两个条件［12］：1）待分析信号的极值数与过零值数相等或最多相差1；2）在任意点上，由局部极值确定的上下包络线均值为零。其中最低频的IMF普遍为原信号的均值或者趋势项，高频的IMF分量一般为噪声。计算式为：

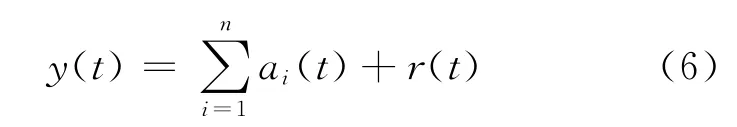
式中，y（t）为原始序列，ai（t）表示获得的IMF本征分量，n为分量总数，r（t）为趋势分量。

2.2 统计评定指标

1）均方根误差（RMSE）为：

其中，N为信号的长度；yt是去噪后的信号；y是原始不含噪声的信号；ut为原始含噪信号；SRMSE为滤波后信号的RMS值，SRMSE越小说明yt和y越相似；NRMSE 为滤波后噪声部分的RMS 值，NRMSE越接近噪声水平，去噪效果越好。

2）互相关系数（R）为：

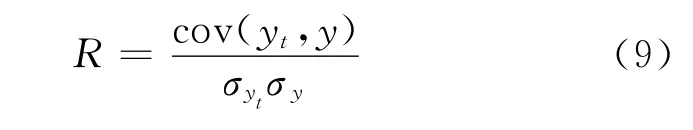
式中，cov（yt，y）是yt和y的协方差，σyt和σy分别是yt和y的标准差。R越大，表示去噪后的信号和原始未含噪的参考信号越相似。

3）信噪比（SNR）为：

3 模拟数据分析

构造模拟数据模型：

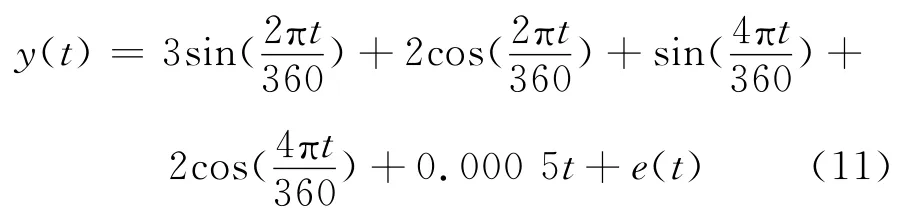
模拟数据的采样频率为1s，样本大小为3 000，主要由两个周期信号叠加而成，e（t）为服从正态分布N（0，1.52）的高斯白噪声，并且加入一个低频的趋势项。3种方法去噪结果如图1所示，从上至下分别是：模拟的原始时间序列；未加噪声的模拟时间序列；去噪后的序列；去噪后的序列与未含噪声序列的残差序列；原始时间序列与去噪后序列的残差序列。

从图1对比可看出，SSA 去噪后的序列与原始未含噪序列的残差序列比较平稳且趋近于零，而小波和EMD 去噪后的残差序列不平稳，且EMD 在端部的残差比较大。为了进一步证明SSA 方法去噪的有效性，采用3种评价指标进行定量比较分析。从表1中可看出，3 种方法去噪后的信号与真实信号的相关系数都达到了0.99以上，说明3种方法均是有效滤波法。从滤波后信号的SRMSE值可以看出，SSA 方法最小，且其滤波后噪声的NRMSE 更加接近噪声水平，SSA方法去噪后序列的信噪比也略高于小波和EMD，以上都说明SSA 方法去噪性能的优越性。

表1 3种方法模拟去噪效果的定量分析Tab.1 Quantitative analysis of the simulation denoise results of three kinds of method

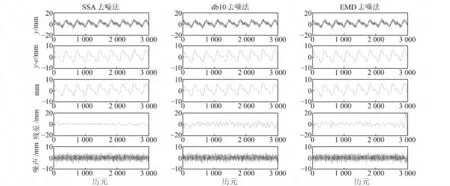
图1 SSA、db10小波和EMD 模拟去噪结果对比Fig.1 Comparison between the simulation denoise results of SSA，db10wavelet and EMD

模拟数据有两个周期函数，分别是：

图2是3种方法分解出来的周期信号分别与原始真实信号s1和s2进行的对比。总体上，3种方法均能有效地从原始含噪信号中分离出s1和s2信号。但SSA 分解出来的s1和s2信号与原始真实信号的残差都比较平稳且趋于零；而通过小波和EMD 方法得到的残差序列不平稳且存在端部效应，说明SSA 方法提取周期项的性能要优于小波分析与EMD 方法。从表2 也可看出，用SSA 方法提取的信号s1和s2与对应参考信号的RMSE要远低于db10小波和EMD，而互相关系数R大于db10小波和EMD，以上都表明SSA 方法对周期性信号提取的优越性。

表2 3种方法分解的信号与对应参考信号的RMSE（mm）和互相关系数RTab.2 RMSE（mm）and correlation coefficients of decomposed signal and the reference signal

图2 SSA、db10小波和EMD 分解的s1信号和s2信号Fig.2 Signal s1and s2derived from decomposition of SSA，db10wavelet and EMD

4 实例分析

图3是采用SSA、db10小波和EMD 三种方法分别对我国IGS站BJFS站的高程序列进行滤波去噪的结果。3种方法去噪后的序列都比较平滑，均能有效剔除序列中每个时间点的高频噪声，但SSA 去噪的序列和db10小波去噪后的序列相关性更高，而EMD 方法由于分解不稳定，存在过度去噪的现象，如图3中红色椭圆标记处。表3是3种方法去噪后的信号互相关系数比较，SSA与小波去噪后的相关系数达到0.995，高于SSA与EMD、db10 小波与EMD 的相关系数，说明SSA 与db10小波去噪后的序列更吻合。SSA 与原始时间序列、db10小波与原始时间序列的互相关系数均为0.868，稍高于EMD 的0.857，说明SSA、db10小波去噪后的信号与原始信号更接近。SSA、db10小波和EMD 去噪后的信号与噪声的信噪比分别为11.118、11.133 和9.863，EMD 的信噪比最低。从以上分析可看出，前两种方法的去噪效果相当，且略优于EMD。

图4是3种方法进行多尺度分解后的结果，由于篇幅限制，只给出db10 小波分解得到的d7～d 1 0分量和EMD的IMF 7～IMF 1 0分量。SSA 方法分解的信号从上往下分别为0.25a、0.5a、1a和似2a周期信号，结果与文献［1］一致；db10 小波分解的信号从上往下分别为：0.5 a、1a、似2a周期信号和周期更长的信号；EMD分解的的信号从上往下分别为：0.5a、1a、似2a周期信号和周期更长的信号。从图可见，SSA 方法分解得到的0.25a、0.5a和1a周期信号在其对应的频率存在明显且单一的峰值，而另两种方法仅1a周期信号比较明显，其余信号则存在周期混叠现象。总之，3种方法均能分解出季节性信号，从贡献率大小看，1a周期信号所占比重最大，0.5a周期信号次之；从分解效果看，SSA 方法提取的季节信号更加稳定平滑，且信号混叠现象不明显。

表4是3种方法对分解的年周期信号进行的相关性分析，SSA 提取的年周期信号与db10 小波提取的年周期信号之间的互相关系数达到了0.96，而SSA 和db10 小波与EMD 之间的互相关系数分别为0.89和0.86，说明SSA 提取的年周期信号和db10小波提取的年周期项信号更接近，且SSA 提取的年周期信号与原始时间序列的相关性要高于db10小波与EMD 的相关性，这表明SSA 提取的年周期项信号更接近于原始时间序列，也间接说明了SSA 方法提取年周期项的优越性。

图3 3种方法的BJFS站高程序列去噪结果Fig.3 The denoise results of BJFS station of three kinds of method

图4 3种方法的多尺度分解结果Fig.4 Multi－scale decomposition results of three kinds of method

表3 SSA、db10小波和EMD去噪后信号的互相关系数RTab.3 Correlation coefficients of three kinds of method denoising for BJFS station

表4 SSA、db10小波和EMD分解的1a周期信号的互相关系数RTab.4 Correlation coefficients of three kinds of method decomposing annual cycle

5 结 语

奇异谱分析是主成分分析方法的一种，主要对一维时间序列进行分析，适用于从短时间序列中提取信息。基于此方法，本文对模拟数据和GPS实测数据进行去噪和周期项提取的研究，并与小波和EMD 方法对比分析。结果表明，3种方法都是有效的去噪方法，且均能较好地分解出季节性信号，但SSA 方法去噪效果更好，分解得到的周期信号更加稳定和平滑，且不存在信号混叠现象。

［1］王解先，连丽珍，沈云中.奇异谱分析在GPS站坐标监测序列分析中的应用［J］.同济大学学报：自然科学版，2013（2）：282－288（Wang Jiexian，Lian Lizhen，Shen Yunzhong.Application of Singular Spectral Analysis to GPS Station Coordinate Monitoring Series［J］.Journal of Tongji University（Natural Science），2013（2）：282－288）

［2］徐克红，程鹏飞，文汉江.太阳黑子数时间序列的奇异谱分析和小波分析［J］.测绘科学，2007，32（6）：35－38（Xu Kehong，Cheng Pengfei，Wen Hanjiang.Singular Spectrum Analysis and Wavelet Analysis on Time Series of Sunspot［J］.Science of Surveying and Mapping，2007，32（6）：35－38）

［3］Vautard R，Yiou P，Ghil M.Singular－Spectrum Analysis：A Toolkit for Short，Noisy Chaotic Signals［J］.Physica D：Nonlinear Phenomena，1992，58（1）：95－126

［4］江志红，丁裕国.奇异谱分析的广义性及其应用特色［J］.气象学报，1998，56（6）：736－745（Jiang Zhihong，Ding Yuguo.Generality and Applied Features for Singular Spectrum Analysis［J］.Acta Meteorologica Sinica，1998，56（6）：736－745）

［5］吴洪宝.奇异谱分析——最大熵预报方法［J］.甘肃气象，2000，18（1）：1－5（Wu Hongbao.Singular Spectral Analysis－Maximum Entropy Forecast Method［J］.Gansu Meteorology，2000，18（1）：1－5）

［6］Ghil M，Vautard R.Interdecadal Oscillations and the Warming Trend in Global Temperature Time Series［J］.Nature，1991，350（6316）：324－327

［7］Jevrejeva S，Moore J C.Singular Spectrum Analysis of Baltic Sea ice Conditions and Large‐Scale Atmospheric Patterns Since 1708［J］.Geophysical Research Letters，2001，28（23）：4 503－4 506

［8］Yoo J C，Dorico P.Trends and Fluctuations in the Dates of Ice Break－up of Lakes and Rivers in Northern Europe：the Effect of the North Atlantic Oscillation［J］.Journal of Hydrology，2002，268（1）：100－112

［9］Rangelova E，Wal W，Sideris M G，et al.Spatiotemporal Analysis of the GRACE－derived Mass Variations in North America by Means of Multi－Channel Singular Spectrum Analysis［M］.Springer Berlin Heidelberg，2010

［10］党星海，赵丽洁，孔令杰，等.小波分析在GPS 振动监测数据中的应用［J］.大地测量与地球动力学，2013，33（2）：147－150（Dang Xinghai，Zhao Lijie，Kong Lingjie，et al.Application of Wavelet Analysis in GPS Dynamic Deformation Data Processing［J］.Journal of Geodesy and Geodynamics，2013，33（2）：147－150）

［11］罗飞雪，戴吾蛟.小波分解与EMD 在变形监测应用中的比较［J］.大地测量与地球动力学，2010，30（3）：137－141（Luo Feixue，Dai Wujiao.Comparison of EMD with Wavelet Decomposition for Dynamic Deformation Monitoring［J］.Journal of Geodesy and Geodynamics，2010，30（3）：137－141）

［12］戴吾蛟，丁晓利，朱建军，等.基于经验模式分解的滤波去噪法及其在GPS 多路径效应中的应用［J］.测绘学报，2007，35（4）：321－327（Dai Wujiao，Ding Xiaoli，Zhu Jianjun，et al.EMD Filter Method and Its Application in GPS Multipath［J］.Acta Geodaetica et Cartographica Sinica，2007，35（4）：321－327）