GNSS多频观测值线性组合研究

郭忠臣 高井祥 王 坚 曹新运

1 中国矿业大学国土环境与灾害监测国家测绘地理信息局重点实验室，徐州市大学路1号，221008

随着GPS、GLONASS 系统现代化以及BDS、Galileo不断完善，多系统多频观测值的出现，使得波长长、电离层误差小以及观测噪声小的组合方式更加灵活［1－5］。为表达方便，各个系统的频率由大到小依次表示为f1、f2、f3、f4（表1），各个频率之间的比例关系见表2。

不同的系数组合产生不同特性的组合观测值，如波长较长、弱电离层、低噪声等［6］，利用这些特性可以有效地提高载波相位整周模糊度解算效率和可靠性［7］。考虑不同系统频率间的组合原理类似，文中以Galileo四频观测值组合为例，分别给出以周为单位和以m 为单位的相位组合观测模型的通用形式，并对各类观测值误差进行详细分析，最后为每个系统给出几组较好的观测组合系数。

表1 当前导航系统频率（k ＝－7，…，＋12）／MHzTab.1 Current navigation system frequency（k ＝－7，…，＋12）／MHz

表2 各频率之间关系Tab.2 Relationship between the frequencies

1 载波相位组合观测值定义

以Galileo系统为例，不考虑多路径效应等误差，单一载波相位观测值方程可表示为［8］：

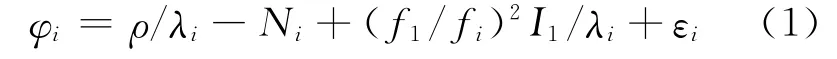
式中，i＝1，2，3，4（下文中i均表示1，2，3，4）；ρ表示站星间几何距离和非弥散项误差；λi、Ni、Ii、εi分别表示相应频率波长、整周模糊度、电离层延迟误差以及观测噪声。四频相位组合观测量的一般形式如下。

1）以周为单位：

式中，φc为组合相位观测值；ai为组合系数，为保持整周模糊度的整数特性，需使ai为整数。由式（2）可求得组合后观测值对应的频率fc、波长λc以及模糊度Nc：

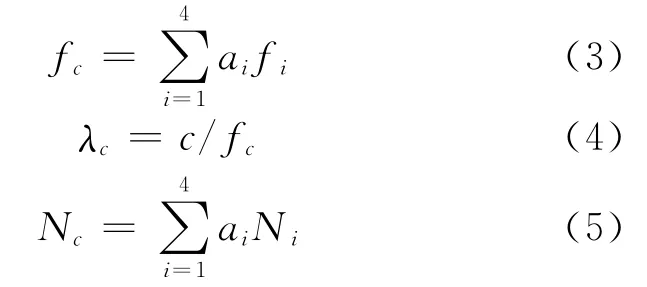
令M1＝λc／λmax，此时f4的波长最长。

2）以m 为单位：

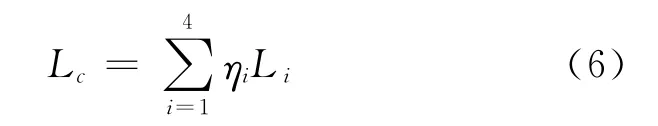
式中，Lc为距离组合观测值；ηi为组合系数，要使组合后站星间的几何距离不变，则需。

由式（2）和（6）比较得：ηi＝aiλc／λi。

2 误差分析

2.1 非弥散项误差

非弥散项误差包括对流层延迟误差、轨道误差等与频率无关的误差项。令单一载波观测量的该项误差为ξi，由式（6）得：

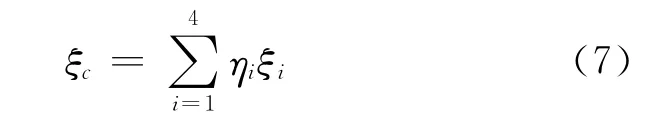
由于该项误差不受频率的影响，故假设该项误差对各频率的影响为ξ0，则有ξc＝ξ0，即组合后观测值所受到的非弥散项误差大小与单一载波相同。

2.2 电离层延迟误差

利用式（2）、（6）可推知，组合后的电流层延迟误差为：

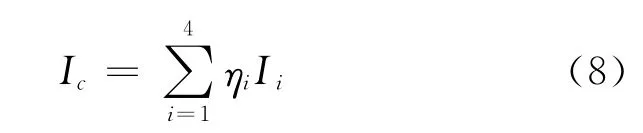
1）以m 为单位：

2）以周为单位：

式（9）和（10）说明，组合载波电离层延迟大小与组合系数有关。

2.3 观测噪声

观测噪声为随机误差，满足误差传播定律。由误差传播定律可知，观测噪声为：

1）以m 为单位：

又因为观测噪声对各个频率的影响互不相关，也可假设其对各频段的影响相同。令L1载波观测噪声为σφ1周，组合观测值观测噪声与单个载波观测噪声之比为M3，此时有

2）以周为单位：

令单个载波观测噪声为σφ周，则有

式（11）、（12）表明，以m 为单位时，组合观测值的观测噪声有可能会比单个载波观测噪声小；以周为单位时，组合观测值的观测噪声总会比单个载波观测噪声大。

3 组合系数的选取

对不同频率观测值进行线性组合，可产生具有不同特性的组合观测值。选取的组合系数应能使组合后观测值满足以下几点［9］：

1）组合后的观测值应保持模糊度的整周特性，以便正确确定整周模糊度；

2）组合后的观测值应该具有适当的频率和波长；

3）组合后的观测值应含有较小的电离层延迟误差和观测噪声。

通过计算机编程计算分别得到各系统具有较好特性的组合，如表所示。

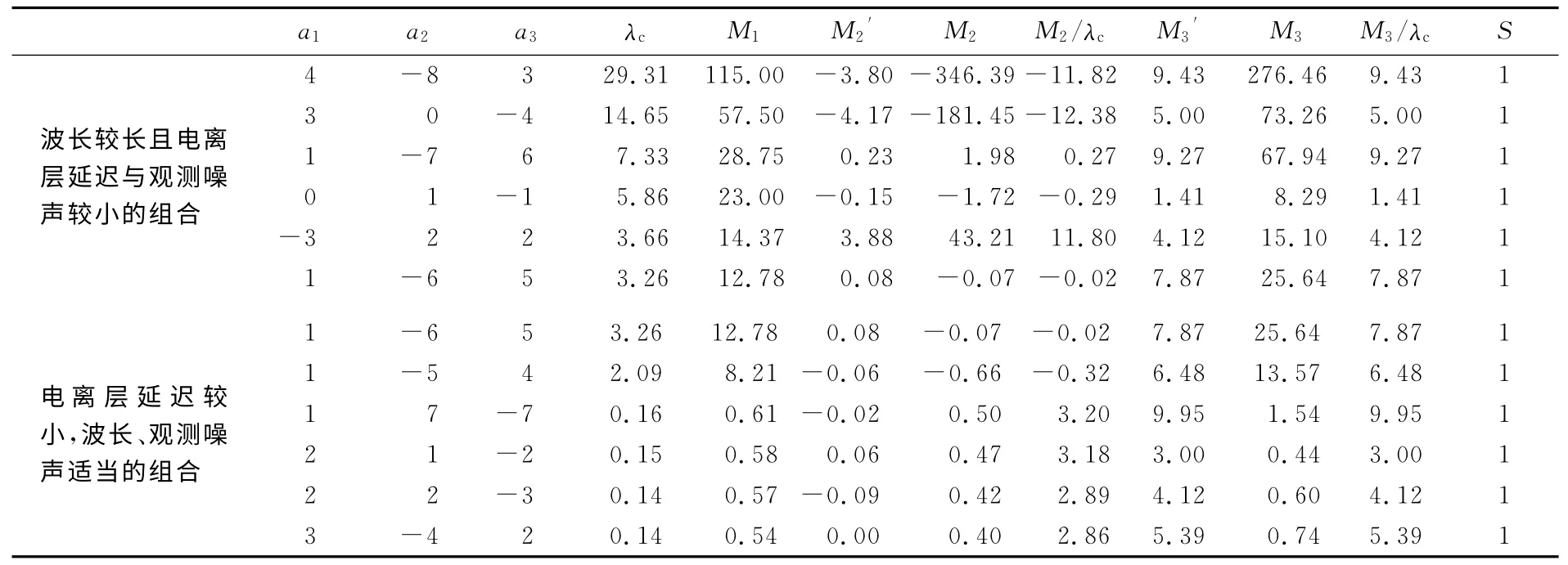
表3 GPS三频观测值线性组合系数Tab.3 GPS triple－frequency observation combination coefficient

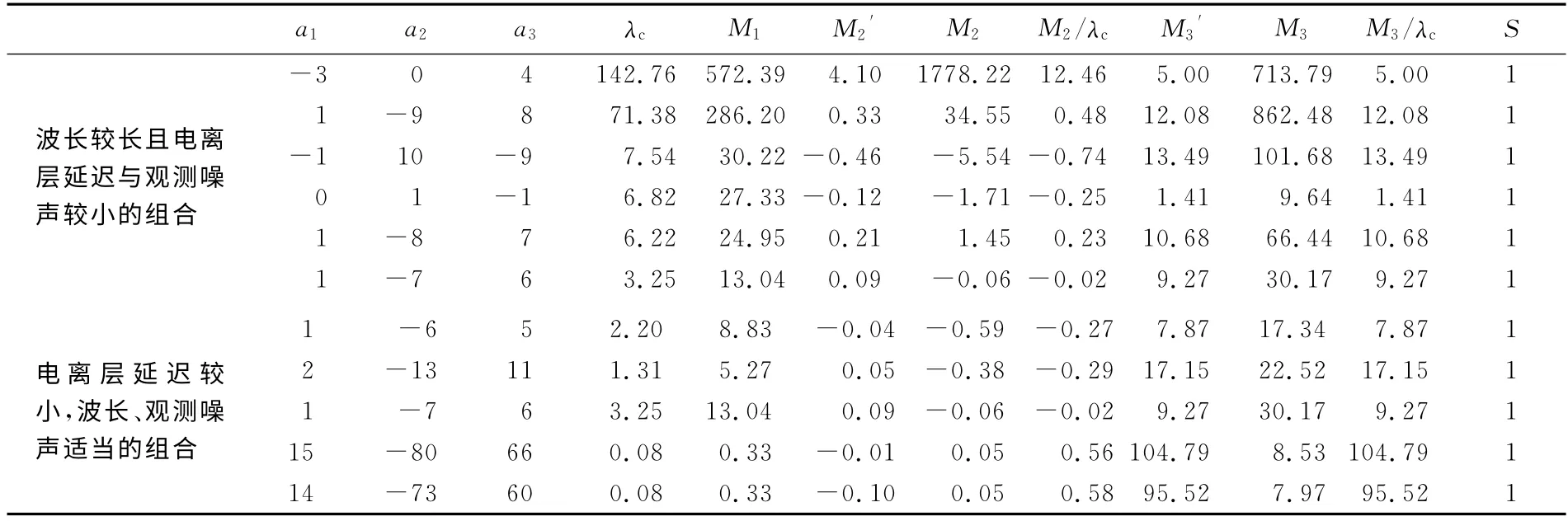
表4 GLONASS三频观测值线性组合系数Tab.4 GLONASS triple－frequency observation combination coefficient

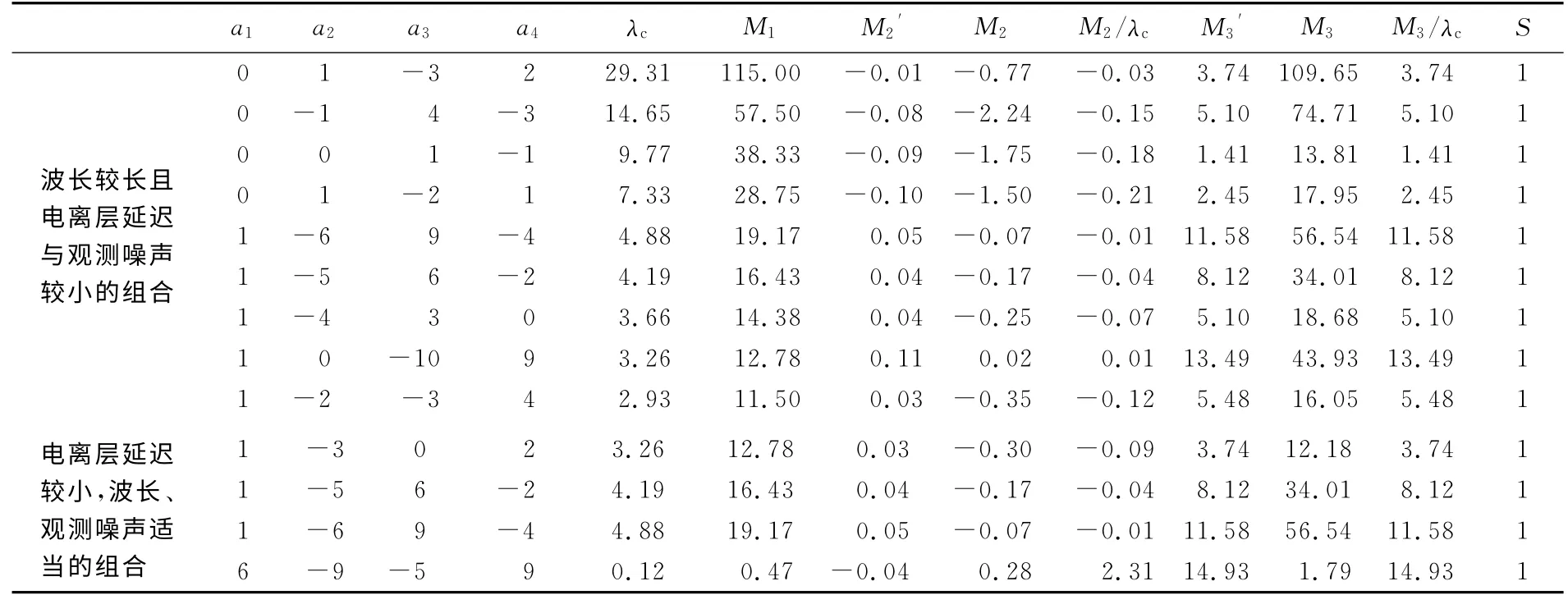
表5 Galileo四频观测值线性组合系数Tab.5 Galileo quad－frequency observation combination coefficient

表6 BDS三频观测值线性组合系数Tab.6 BDS triple－frequency observation combination coefficient

双差解算短基线时，两站的大气延迟相关性强，可通过求差来削弱其影响，这时需要波长较长且精度高的组合观测值；长距离相对定位时，则需要波长较长且电离层延迟误差较小的组合进行解算［3］。表中，部分组合能产生较大的波长，但此时电离层延迟误差和观测噪声也会比较大，这类组合在短基线的双差解算中，可以通过双差削弱其影响，而且由于其波长比较长，可以快速确定其整周模糊度，如表7中的Coe＿comb1列；一些系数组合后的观测值虽然波长不长，但是其电离层延迟和观测噪声的影响比较小，如Coe＿comb2列；还有一类组合是有较长的波长，电离层延迟与观测噪声都相对较小，这类组合在长、中、短基线下都能比较容易地固定其整周模糊度，并满足快速定位对定位速度和定位精度的要求，如Coe＿comb3列。

表7 几种典型的组合系数Tab.7 Several typical combination coefficient

4 结 语

本文对4个卫星导航系统的不同频率进行线性组合，并编程计算了能满足一定标准的组合系数。不同的系数组合具有不同的特性，可在不同的条件下使用，以提高导航定位的效率。本文给出了几组典型的系数组合，该组合在基线解算过程中能快速确定整周模糊度。在未来10a内，随着全球卫星导航系统的发展，全球将会出现4大卫星导航系统共存互补的局面［10］，卫星发射的频率将会越来越多，也将会获得更多的载波相位观测数据，以形成更多更灵活的组合方式。

［1］陈俊勇.美国GPS现代化概述［J］.测绘通报，2000（8）：44－45（Chen Junyong.Brief Introduction of GPS Modernization in USA［J］.Bulletin of Surveying and Mapping，2000（8）：44－45）

［2］徐军，陶庭叶，高飞.GLONASS 三种载波频率组合值研究［J］.大地测量与地球动力学，2013，33（1）：86－89（Xu Jun，Tao Tingye，Gao Fei.Research on Three Kinds of Carrier Frequency of GLONASS［J］.Journal of Geodesy and Geodynamics，2013，33（1）：86－89）

［3］王泽民，柳景斌.Galileo卫星定位系统相位组合观测值的模型研究［J］.武汉大学学报：信息科学版，2003，28（6）：723－727（Wang Zemin，Liu Jingbin.Gailieo Satellite Positioning System Phase Combination Observation Model Research［J］.Geomatics and Information Science of Wuhan University，2003，28（6）：723－727）

［4］杨元喜.北斗卫星导航系统的进展，贡献与挑战［J］.测绘学报，2010，39（1）：1－6（Yang Yuanxi.Progress，Contribution and Challenges of Compass／Beidou Satellite Navigation System［J］.Acta Geodaetica et Cartographica Sinica，2010，39（1）：1－6）

［5］曹新运，王坚.GPS三频非差观测值探测与修复周跳［J］.武汉 大 学 学 报：信 息 科 学 版，2014，39（4）：450－455（Cao Xinyun，Wang Jian.Cycle－Slip Detection and Repair Using GPS Triple－Frequency Un－differenced Observations［J］.Geomatics and Information Science of Wuhan University，2014，39（4）：450－455）

［6］伍岳，郭金来，孟央，等.GPS 多频相位组合观测值的定位精度分析［J］.武汉大学学报：信息科学版，2006，31（12）：1 082－1 805（Wu Yue，Guo Jinlai，Meng Yang，et al.Analysis of GPS Multi－Frequency Carrier Phase Combinations［J］.Geomatics and Information Science of Wuhan University，2006，31（12）：1 082－1 805）

［7］陈宇，白征东，原波.整数规划在三频组合观测值确定中的应用［J］.大地测量与地球动力学，2010，30（6）：116－119（Chen Yu，Bai Zhengdong，Yuan Bo.Application of Integer Programming for Determining Triple－Frequency Observations［J］.Journal of Geodesy and Geodynamics，2010，30（6）：116－119）

［8］李征航，黄劲松.GPS测量与数据处理［M］.武汉：武汉大学出版社，2007（Li Zhenghang，Huang Jinsong.GPS Surveying and Data Processing［M］.Wuhan：Wuhan University Press，2007）

［9］唐保华，刘庆元，王虎.GPS三频组合观测值的研究［J］.矿山测量，2007（3）：17－18（Tang Baohua，Liu Qingyuan，Wang Hu.Research on GPS Triple－Frequency Phase Combination Observations［J］.Mine Surveying，2007（3）：17－18）

［10］孙家栋.北斗卫星导航系统发展之路［J］.太空探索，2010（7）：31（Sun Jiadong.Development Approach of Beidou Satellite Navigation System［J］.Space Exploration，2010（7）：31）