利用学生错误资源提高数学教学效益

◎福建省上杭县明强中学 范景山

利用学生错误资源提高数学教学效益

◎福建省上杭县明强中学 范景山

学生在掌握前人经验、探求新知的过程中，难免会出现这样或那样的错误．而他们也正是在教师的精心指导下，在不断的纠错过程中渐渐成长、成熟，最终走向成功的．因此，作为数学教师，在自己平时的教学过程中要善于捕捉学生的错误信息，并把该信息当作一种教学资源，追根溯源，找出错误原因，及时地帮助学生从错误的漩涡中跳出来，开展有效的数学课堂教学．

学生错误资源；有效；数学课堂教学

众所周知，人对事物的认识是一个循序渐进的过程，是一个从无知到有知，从知之不多到知之较多，从肤浅到深刻的不断提升的过程.学生对知识的掌握也是同样的道理.数学是研究现实世界的空间形式和数量关系的科学，抽象性、科学性和应用的广泛性是数学的主要特点.学生的知识学习，就是掌握前人的经验，把人类共同的精神财富变为自己的精神财富.数学学习的建构学说认为：“数学知识不能从一个人迁移到另一个人，一个人的数学知识必须基于个人对经验的操作、交流，通过反省来主动建构.”然而，学生在掌握前人经验、探求新知的过程中，难免会出现这样或那样的错误.而他们也正是在教师的精心指导下，在不断的纠错过程中渐渐成长、成熟，最终走向成功的.因此，作为教师，在自己平时的教学过程中如何捕捉学生的错误信息？如何把该信息当作一种教学资源，及时地帮助学生从错误的漩涡中跳出来，开展有效的课堂教学？都是非常值得我们关注与思考的问题.

一、实验举证，捕捉错误信息

学生对数学知识的错误认识和应用往往来自于对该知识的不求甚解，其结果必然与真理存在偏差.因此，要帮助学生找出这些偏差，关键要帮助他们理解概念、定义、定理及公式等的来龙去脉.

【案例1】高中数学必修4第113页A组第4题：平面上三个力F1、F2、F3作用于一点且处于平衡状态，F1=N，F1和F2的夹角为45°，求：（1）F3的大小；（2）F3与F1夹角的大小.

当学生出现这种错误时，教师要有耐心.首先，你可提问学生：“这种做法对吗？如果对，请说出其依据是什么；如果错，请说出其错误的原因.”这种提问的方式，可以充分调动学生的思维积极性，大大激发学生的学习热情，学生就会主动地去的思考和观察.

我们可以给学生做这样一个实验：将一个10克的砝码挂在两个相同的弹簧秤的秤钩上，使两弹簧秤之间的夹角为120°（它们与铅直线的夹角均为60°），当砝码处于平衡状态时，让学生们观察，弹簧秤的指数是否均为5克？通过观察，学生们发现弹簧秤的指数均为10克.

可见，实验与观察并举是发现错误的一个直观而有效的检验手段.

【案例2】学生在开始学习两角差的余弦公式时，往往会记成cos（α-β）=cosα-cosβ.为了帮助学生发现此类错误，教师可通过设问的方式引导他们采用赋值检验法.如α=90°，β=45°时，等号左边的值为，而右边的值为.显然，这时cos（α-β）=cosα-cosβ是不成立的.进而发现，自己已将公式记错了.

【案例3】学生在开始学习等差数列｛an｝的性质时，往往会记成am+an=am+n（m，n∈N*）.为了帮助学生发现此类错误，教师可通过设问的方式引导他们也采用赋值法，即特值检验法.如对任意一个非零的常数列，将其代入检验后，上式均不成立.进而让学生发现，自己已将公式记错了.

二、追根溯源，找出错误原因

当学生发现错误后，作为教师，首先应该鼓励他们：“你们已经进步了，因为正确的认识往往是从发现错误开始的.”

其次，教师再激励学生：“当一个人认识错误后，更需要很好地改正错误，而要彻底地改正，又更需要找到犯错的根本原因.你们说，是吗？”学生们异口同声：“是！”

师：“那么，案例1的第（1）小题中的错误解答F3=，到底错在哪里？为什么不能像‘数的加法’一样去做加法运算呢？”学生无言以对.

师：向量的定义是什么？

生：向量是既有大小又有方向的量.

师：数与向量有何区别？

生：数是只有大小的量.

师：因此，向量的加法能等同于数的加法吗？

教师通过这样的循循善诱，终于让学生明白了刚才的错误所在.

分析发现，刚才的错误正是暴露了学生对“向量加法”的错误理解，其错误在于将“向量加法”与“数的加法”混为一谈，其根源在于对“向量”的理解等同于对“数”的理解.

再看案例2中的错误cos（α-β）=cosα-cosβ和案例3中的错误am+an=am+n（m，n∈N*），通过分析也发现，学生没有掌握公式的来龙去脉，进而无法对公式进行实质性的理解，导致对公式的记忆显得肤浅毛糙、不求甚解，学习跟着感觉走.

三、探寻秘方，对症下药

当学生找到了错误根源后，教师应该趁热打铁，提出一些启发性的问题，想办法打开学生的思维大门，让学生主动地去寻求解决问题的有效途径.

再回过头来看，案例1中F3=F1+F2=F1+F2的错误应改为

师：F1+F2=？

学生顿时恍然大悟，并争相着回答：F1+F2=

可见，教师适时适度的启发诱导是打开学生思维大门的催化剂.

接着，我继续开展与学生互动的教学.

师：如果按原来的错误解法去做，那么题中的条件“向量F1和F2的夹角为45°”又有何意义呢？

听了这一提问后，学生们对式子F1+F2=F1+ F2的错误有了更为深刻的认识.

师：向量的模的公式a=？，进而提出F3与F1、F2关系如何？

生：a=a2，且F1+F2=-F3.

师：如何利用这两个等式去求F3呢？

听了这样的启发之后，学生们顿时豁然开朗.

再看案例1中的第（2）小题？

师：如图所示，设力F1和F3的夹角为θ，则.显然，分母的值容易算，但分子的值又该如何去算呢？顺着学生的这种错误思路，指出此法行不通.

生：那该怎么办？

师：F1和F2的合力是F3′，它与力F3构成怎样的关系？

生：互为相反向量.

师：换过一种思路，我们能否利用F3′与F1的夹角π-θ来考虑？cos（π-θ）=?

师：这样看来，应该另寻一条出路.由于F1+F2=F3′，因此我们可以得到F2=F3′-F1，于是有F22=（F3′-F1）2，即

师再问：F3·′F1=？

生：F3′·F1=F3′·F1·co（sπ-θ）.

师：至此，同学们能求出θ了吗？

生（异口同声）：能！

作为教师，我们这时就应及时地对他们的回答给予积极鼓励，让他们真正体验到“在快乐中学习，在学习中快乐”.

四、变式训练，夯实知识根基

所谓数学变式训练，即是指在数学教学过程中对概念、性质、定理、公式以及问题进行不同程度、不同层次、不同情形、不同背景的变式，以暴露问题的本质特征，揭示不同知识点间的内在联系的一种教学设计方法.它是优化课堂教学的重要手段，在训练中能有效改善学生的解题现状，利用转化发散学生思维，增强学生分析、解题能力.

比如，在掌握了案例1后，我们可进行下面的变式训练：

变式1.已知F1=1，F2=2，F1和F2的夹角为60°，以F1和F2为邻边作平行四边形，求此平行四边形的两条对角线中较短的一条的长度.

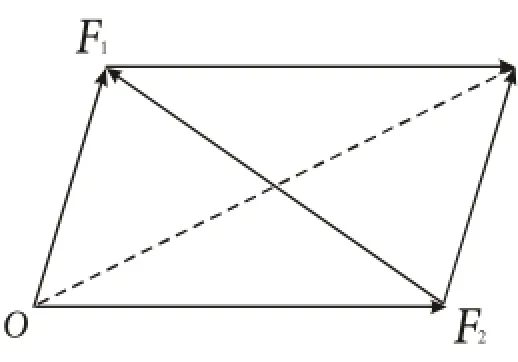
师：接下来又怎样计算F2F1呢？

师：接下来，如何利用已知条件F1和F2的大小（即的大小）及其夹角60°计算呢？

观察学生的神情，看似有点遗忘，教师因势利导，再加以启发.

通过这样的一番启发之后，学生们顿时豁然开朗，争相着回答.这时，教师可以叫学生到黑板上板演.很快，学生就做出来了：

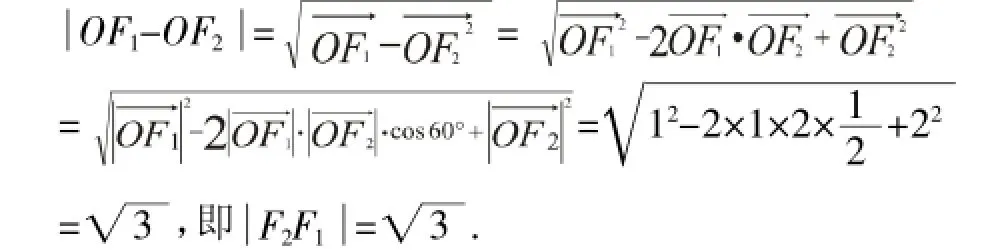
至此，问题得到了圆满的解答.

下面就可以让学生练习变式2与变式3.

经过以上变式训练之后，教师可以帮助学生总结一下：“这些题目的解法有什么共同之处？均采用了什么公式？对我们今后的解题能带来什么启发与思考？”

五、反思错误，培养优良学习品质

古人云：“学而不思则罔.”这也就是人们常说的“铁不用就会生锈，水不流就会发臭，人的智慧不用就会枯竭”.思考可以使人对知识理解得更深刻，思考可以使学的东西更扎实，未来社会最需要的就是善于思考、敢于创新的人.

而反思就是对自己经历过的思想、心理感受及行为的体验和思考，它是一种更能促进自身发展的思考.爱迪生说过，如果一个人在学习中有了反思的习惯，那么他必将是成功的学习者.

比如，在帮助学生解答完案例1时，教师可以采用反问的方式，总结一下学生所犯过的错误.

师：在案例1中，你们为什么会出现F1+F2=F1+ F2的错误呢？

师：那应该怎么用呢？

……

其实，教师巧妙的设问教学（尤其是反问）可以很好地培养学生“学会反思”这种优良的学习品质.

用心对待教育和教学，用心对待学生，我们就会把学生的错误当作一种可开发和利用的宝贵的教学资源.只有这样，我们的教育和教学才会有效而生动，才会富有强大的感召力和永恒的生命力！

（责任编辑：王钦敏）