“函数的单调性”教学简录*

●史 嘉 (亳州市第一中学 安徽亳州 236800)

“函数的单调性”教学简录*

●史 嘉 (亳州市第一中学 安徽亳州 236800)

1 教学背景介绍

第7届全国高中青年数学教师优秀课展示与培训活动于2014年12月6日～9日在重庆举行．活动贯彻“深化课程改革、落实立德树人根本任务”的新精神，推动我国高中数学教学研究与改革，促进高中青年数学教师树立德育为先、能力为重、全面发展的教育理念．笔者有幸代表安徽省参赛，并获得一等奖(被评为最优秀选手之一)，参赛课题是中国教育学会中学数学教学专业委员会指定的8个课题之一“函数的单调性”．

2 先行组织者

以增函数为例，初中阶段用“图像上升”和“y随x的增大而增大”来描述，前者直观形象，后者通俗易懂，但都不准确严谨，无法进行严格的数学推理论证．事实上，单调性是函数在区间上变化时一种保持不变的特征，如何用静态的数学符号刻画动态的函数变化趋势呢?

3 教学目标及重点、难点

3．1 课堂教学目标

1)理解函数单调性的相关概念，并能准确、规范地表述;

2)理解函数单调性的形式化定义，初步掌握判断和证明简单函数单调性的方法;

3)经历对单调性完整的认知过程，锻炼观察归纳、抽象概括和推理论证能力，从而体会数形结合等思想，体验数学的理性精神和内在力量．

3．2 教学重点

理解函数单调性的形式化定义．

3．3 教学难点

函数单调性形式化定义的生成性突破．

4 教学过程简录

学习单1创设情境，明确概念

问题1科考队对沙漠气候进行科学考察，图1是某天气温随时间的变化曲线．请你根据曲线图说说气温的变化情况．

师:谁来说说气温有什么变化?想好的请举手示意．

生1:温度有时候升高，有时候降低．还有，温度有最低值约－4℃，最高值约24℃．

师:很好．他关注到2个点:一是随着时间的变化温度有时是下降的，有时是上升的;二是温度的最低值和最高值．那气温什么时候下降，什么时候上升?

图1

生1:从0～6点是下降的，从6～17点是上升的，从17～24点又是下降的．

师:哦，这样就更加明确了气温何时有怎样的变化．(示意坐下)谁还有不同的观点?

生2:从曲线图上可以看出这一天的气温变化幅度比较大．

师:哦!生2关注的是气温变化幅度，也就是温差比较大．这反映的正是沙漠独特的气候——早穿棉袄……

众生:午穿纱，围着火炉吃西瓜．

师:同样一幅图，同学们的关注点是不同的．我们这节课要关注的是函数图像上升和下降的变化情况．

问题2函数是描述事物变化规律的数学模型．如果清楚了函数的变化规律，那么就基本把握了相应事物的变化规律．在事物变化过程中，保持不变的特征就是这个事物的性质．因此，研究函数的变化规律是非常有意义的．

观察下列函数图像，请你说说这些函数有什么变化趋势?

生3:图2是上升的，y随……

师(打断生3):我从这边看(从右往左)怎么是下降的呢?

生3:从左向右看是上升的，y随着x的增大而增大;图3是先下降后上升……

图2

图3

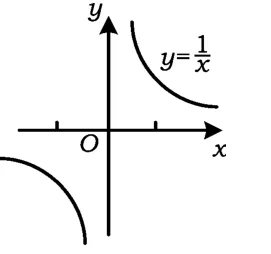
图4

师(再次打断生3):什么时候下降，什么时候上升?

生3:当x＜0时，图像下降;当x＞0时，图像上升．图4当x＜0时图像下降，当x＞0时图像也是下降．

师(示意生3坐下):好!生3不仅回答了函数图像的变化趋势，还说到了y随x的变化情况．我们表述时，一定要说清楚函数在哪个区间上具有怎样的单调性．

通过观察3个函数的图像，回顾初中描述函数单调性的图形语言和自然语言．进一步明确单调性的相关概念后，再次借助图1准确表述函数的单调性(略)．

学习单2设置问题，形成冲突

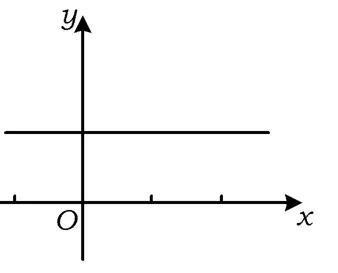
图5

问题31)给出函数y=f(x)的 图 像 (以 f(x)=0．001x+1 为例)，它在定义域R上是单调递增的吗?

师:看来，函数是单调递增的还是单调递减的，看图像非常直观，一目了然．请注意了，这个函数(如图5所示)是增的吗?

众生:不是．

师:那是怎样的呢?

生(众):平的．

师:呵呵，平的，不变的．请看它的解析式(推出f(x)=0．001x+1)，增的还是减的?

生(众):增的．

师:看图是不是不直观了呀，我们需要结合解析式．再来看一个函数(推出图3)，这个函数在(0，+∞)上是增的还是减的?

个别学生回答“可能是增的”，追问“你怎么判断是增的”，以此形成认知冲突．

师:函数图像不可靠，解析式也不明朗．那该怎么办呢?看来，我们必须要重新研究单调性了．

学习单3引导探索，生成新知

问题41)如何理解“y随x的增大而增大”，或者说怎样用数学符号描述函数图像的“上升”特征?

以二次函数f(x)=x2在区间［0，+∞］上的单调性为例，用几何画板动画演示“y随着x的增大而增大”，生成表格(每秒钟生成一对数据，共15对)．

师(交代点M的坐标及运动方式，点击“动画点M”表格递次增加):我让点M动起来，(稍停)怎么样——有什么感受?

众生:y随x的增大而增大．

师:随着点M的运动，自变量x逐渐增大，因变量y也跟着增大．几何画板非常动感地给我们演示了“y随x的增大而增大”．那么，我们该如何用数学符号表示这一变化趋势呢?有想法的同学，举手告诉老师．

生4:假如 x1和 x2都在区间［0，+∞)上，且x1＜x2，如果对应的y1也小于y2，则说明“y随x的增大而增大”．

师(倾听学生的回答，并转述在黑板上):x1，x2∈［0，+∞)，x1＜x2，若 y1＜y2，则说明“y随 x的增大而增大”．同学们赞同他的说法吗?

师:赞同，好．同学们有这种想法非常好．看看能否解决这个问题．

(教师展示下列问题2)和直线单调递增的函数图像．)

2)已知a＜x1＜x2＜b，若f(a)＜f(x1)＜f(x2) ＜f(b)，能保证函数 y=f(x)在区间［a，b］上单调递增吗?

师:在区间［a，b］上，我就按照生4所说的取这样2个点，能保证函数在区间［a，b］上是单调递增的吗?

学生讨论，教师巡视，稍后学生举手发言．

生5:我认为不能保证单调递增．因为取2个点并不能保证x1和x2之间单调递增．

师:咦，你看这图像，这不是单调递增的吗?

生5:可以是单调递增的，但是……

师(等待):呵呵，生5犹豫了．谁来补充一下?

生6:并不能保证一定是单调递增的，可以不是直线．

师:可以是什么线?

生6:可以是曲线，(手势)可以先减后增，也可以先增后减．

师:噢，中间可以有变化，对吧．我们来演示一下生6的想法．(拖动“点M”改变函数y=f(x)在区间［x1，x2］上的图像)x1和x2对应的2个点有没有动?

生(众):没有．

师:哦，但函数图像可以有很多变化．看来，取2个点满足生6所说的要求，并不能保证函数是单调递增的．

师:那我取3个点，满足生6所说的要求，能不能保证函数单调递增呢?

(教师展示下列问题3)和直线单调递增的函数图像．)

3)已知a＜x1＜x2＜x3＜b，若有f(a)＜f(x1)＜f(x2)＜f(x3)＜f(b)，能保证函数y=f(x)在区间［a，b］上单调递增吗?

生(众):不能．

师:谁来说说你的理由?

生7:和刚才的一样，只能保证这3个点单调递增，但是在x1和x2之间的变化趋势不知道，在x2和x3之间的也不知道．

师:非常好!也就是说，我们不知道x1和x2之间的变化情况，同样，也不知道x2和x3之间的变化．我们来演示一下生7的想法．

拖动“点M”，让学生观察函数y=f(x)在区间［x1，x2］和［x2，x3］上的变化．

师:取2个点满足生6所说的条件，不能保证函数单调递增;取3个点，也不能保证单调递增;那取4个点，取8个、10个点，取很多点，取无数多个点满足生6所说的条件，能不能保证函数单调递增呢?同学们请看下列问题4):

4)已知a＜x1＜x2＜x3＜x4＜…＜b，若有f(a)＜f(x1)＜f(x2)＜f(x3)＜f(x4)＜…＜f(b)，能保证函数y=f(x)在区间［a，b］上单调递增吗?

(学生讨论，教师下去摸清认为“可以”的有哪些学生．)

师:有结果了吗?认为“可以”的同学请举手，说说你的理由．

生8:如果在区间［a，b］上取无穷多个点的话，(对应的)这些点就可以组成函数的图像．而这些点都满足条件，因此可以保证函数单调递增．

师:哦，无穷多个点就可以组成函数图像，你认为是“可以”的．有没有不同的意见?

(教师不急着让生8坐下．)

生4:我认为不能说明函数在区间［a，b］上单调递增．

师:你的理由是……

生4:因为虽然取了无数多个点，但是在x1和x2，x2和x3之间总会有些间隔，而在这些间隔里的变化是不清楚的．

师:你去画个图吧，有图有真相，构造图像，一目了然．

生4(到讲台上边画图边讲解):x1和x2之间肯定有间隔，因为毕竟它们是2个点．我们可以放大了看:取出x1和x2，虽然f(x1)＜f(x2)，但是在x1和x2之间还是可以有变化(顺势画出类似正弦函数的曲线)，因此我认为并不能保证函数单调递增．

生8(还没等生4回到座位):我不同意生4的看法．因为函数图像是一条线，线是由点组成的，无数个点就组成一条线．这些点都满足条件，不就说明函数是单调递增的吗?

生4:无数个点，但归根结底还是点，在2个点之间还是有很小的空隙，在很小的空隙里还是可以上下波动的．

生8:无数多个点，2个点之间的空隙会无穷小．

生4:再无穷小，还是有空隙．

师:呵呵，看来2位同学开始“循环”了．旁观者更清楚，谁来帮他们辨一辨?首先表明你的观点，你赞同谁?

生9(主动要求上黑板画图讲解):我赞同生4的观点．除了 x1，我在区间［x2，b］上取无数个点，满足题目要求吧?但在x1和x2之间可以这样(画出单峰函数)，你能说函数是单调递增的吗?

师(转向生8):你现在认为怎么样?

生8(不好意思地说):他们对了，我错了．

(众生笑．)

师:都请坐下!其实他俩争论的焦点在于“无数个点”与“所有的点”的问题．“无数个点”是不是等于“所有的点”?

生(众):不是．

师:其实我们也可以这样构造反例(画出逐渐上升的波浪形曲线，拿尺子画一条与其有很多交点的直线)，在区间［a，b］上可以一直画下去，这无数个交点是不是都满足题意?你说能保证函数是单调递增的吗?

生(众):不能．

师:这下麻烦了——2个点不行，3个点不行，无数多个点还不能保证是单调递增的，那该怎么办呢?

生(众):取任意2个，取所有的，全部取完……

师:对，如果每一个点、所有的点都满足要求，是不是就保证单调递增了?

生(众):是的．

师:这所有的点，你怎么能取完呀?你能一个一个去验证吗?

生(众):不能．

师:那该怎么办呢?

生(众):取任意2个……

师:取所有的点不仅办不到，更不可能去一一验证．其实我们在学习集合的时候遇到过类似的问题，请看子集的概念……

PPT展示教材上子集的定义，提炼出“任意……都……”的关键字词和句式，再次体验对“任意一个”进行操作，突破“无限”的数学思想．学生归纳出增函数定义，并类比得出减函数定义．

学习单4学以致用，理解感悟

判断题你认为下列说法是否正确，请说明理由(举例或画图)．

1)设函数y=f(x)的定义域为［a，+∞)，若对任意x＞a，都有 f(x)＞f(a)，则 y=f(x)在区间［a，+∞)上单调递增;

2)设函数y=f(x)的定义域为R，若对任意x1，x2∈(a，+∞)，且 x1＞ x2，都有 f(x1) ＞ f(x2)，则y=f(x)单调递增;

1)在(0，1)上单调递减;

2)在(1，+∞)上单调递增．

学习单5回顾总结，深化认识

课堂小结1)如何定义函数单调性?为什么要“任意”?

2)研究函数单调性的基本思想和方法是什么?

3)请你谈谈对这节课的感受．

学习单6布置作业，拓展延伸

课堂作业1)第38页习题2-3A组的第3题和第5题;

探究题向一杯水中加一定量的糖，糖加得越多糖水越甜．请你运用所学数学知识解释这一现象．

安徽省教育规划课题《“文化数学”理念下高中数学学习单的实践研究》(项目编号:JG13105)的概念部分阶段研究成果．