一道有关正方体轨迹问题的探讨

●陈华云 (温州市第二外国语学校 浙江温州 325015)

一道有关正方体轨迹问题的探讨

●陈华云 (温州市第二外国语学校 浙江温州 325015)

2015年5月浙江省温州市高中数学学业水平考试适应性测试的选择压轴题如下:

例1 如图1，在正方体ABCD-A1B1C1D1中，动点P在底面ABCD上，并且满足∠BD1P=45°，则动点P的轨迹为( )

A．圆弧 B．椭圆的一部分

C．双曲线的一部分 D．抛物线的一部分

(正确答案:C)

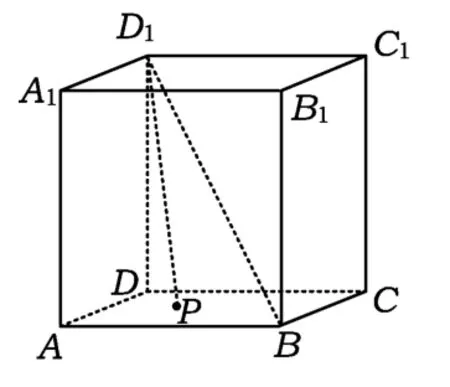
图1

图2

表1 二元二次方程与相关图形

(教师追问:能否通过改变建系的方法，化简上述方程的形式?)

图3

比较以上2种解法，由于不同的建系方法，导致结果形式不同，解法2更易判定为双曲线方程，实际上解法1也可通过坐标系旋转变换公式

(教师:此时问题已经得到解决，但过程有些曲折，能否进一步利用圆锥曲线模型进行分析?)

结论用一个不过圆锥面顶点的平面去截一个圆锥面，当平面与圆锥面的所成角θ与轴截面顶角的半角α大小关系不同时，交线的不同情况如图4所示:1)当α＜θ＜时，交线为椭圆;2)当0≤θ≤α时，交线为双曲线;3)当θ=α时，交线为抛物线．特别地当θ=时，交线为圆．

图4

解法3易知 α=45°，θ=∠D1BD，而tanθ=＜1=tanα，从而0≤θ＜α，故轨迹为双曲线的一部分．

利用解法3的思路，容易解答以下的高考试题:

例2如图5，斜线段AB与平面α所成的角为60°，B为斜足，平面α上的动点P满足∠PAB=30°，则点P的轨迹是 ( )

A．直线 B．抛物线 C．椭圆 D．双曲线的一支

(2015年浙江省数学高考文科试题第7题)

变式1将“动点P在底面ABCD上”改为“动点P在底面ADD1A1上”．

根据对称性特点，同原题得到点P的轨迹为双曲线的一部分，故选C．

图5

图8

解法2本题可参照2008年浙江省数学高考理科试题第10题，其实是一个平面斜截圆柱表面的问题．点P在以D1B为轴线的圆柱面上，又在平面ABCD内运动，则点P在圆柱面与平面的交线上，且满足平面与圆柱的轴线斜交，从而可得点P的轨迹为椭圆，故选B．

注:根据平面与圆柱的轴线的不同位置得到不同截面形状(如图8所示)．

解析几何中的圆锥曲线是平面截圆锥面所产生的截线，从轨迹观点来看，又是空间中动点运动的轨迹．通过一道学考试卷中有关正方体轨迹问题的探讨，让我们更清晰地知道怎样抓住数(定量分析:通过建系、列式求方程，再判断形状)与形(定性分析:需要深入了解曲线的定义与由来，再进行判定)2个角度解决此类问题．