重视借题“发挥” 提高学生学习效能*

●郭建华 孙西洋 (南京市第二十九中学 江苏南京 210036)

重视借题“发挥” 提高学生学习效能*

●郭建华 孙西洋 (南京市第二十九中学 江苏南京 210036)

高三数学复习时间紧、任务重，特别是二轮复习．如何合理精选习题、科学设计教学、通过习题教学提升高三复习效益，是每一位高三一线教师认真思考的一个课题．

《高中数学新课程标准》强调:教师要让学生体验数学知识的发生、发展过程，使学生能够从中发现问题、提出问题，了解知识的来龙去脉，使数学学习成为再发现和再创造的过程．而数学课堂设计借试题“发挥”，恰当地设置前置问题，目的是让难以解决的问题扩大其“最近发展区”，为顺利解题作好铺垫，为学生搭建思维的脚手架，让学生尝试成功的喜悦，同时调动学生探究的积极性，拓展学生的思维，以此提升高三数学复习效益．

1 题目展示

图1

笔者所教的班级是一个基础较好的理科班．笔者先让学生独立思考，然后交流成果．

1．1 借答案不同，正本清源

师:好的，请你说说是怎么得到m+n=2的?

生2:当动圆Q的圆心为点C时，与边BC交于点T，T恰好为BC的中点，联结AT，此时m+n=2．

师:真不错，生2肯动脑筋．问题是你怎么知道m+n=2就是最小的呢?还有没有比2更小的值呢?

(生2思考了一会，不知道怎么说明2就是最小值．)

师:大家知道系数λ1，λ2具有什么性质吗?生3:当 λ1+λ2=1时，点 A，P，B 共线．

师:当λ1+λ2≠1时，点P与直线AB又有什么样的位置关系呢?

生3:当λ1+λ2越大时，点P距直线AB的距离越大．

师:你是怎么知道的?

生3:画草图，观察出来的．

(教师让其他同学都动手画草图，验证该结论是否正确．)

师:大家能否尝试证明这个结论呢?

(教师巡视，让学生自主探究证明其结论．)

图2

即x+y＞1．又过点P有且只有1条直线l与直线AB平行，再利用三角形相似性，易知直线l上每一个点对应的x+y值均为λ．因此点P距直线AB的距离越大，对应的x+y的值就越大．反之，也成立．

师:很漂亮，请同学们利用这个结论证明哪个答案是正确的．

于是生4给出其证明过程:

联结BF，则BC⊥BF，作BF的平行线与以C为圆心的圆相切与于点T(即线段BC的中点)，即点P在点T处时，m+n取得最小值．同理，可求得m+n的最大值为5．

(学生的疑惑终于解决了，教室里响起了一片掌声……)

师:下面，请同学们通过一组变式练习，来巩固刚才大家学习的成果．

图3

图4

点评以上2道变式训练题均以平面几何为背景，是融向量与最值为一体的综合问题，难度较大．考虑到几何图形的特殊性，恰当地建立平面直角坐标系，以坐标系为桥梁，用坐标和方程表示其中的几何元素，再结合线性规划思想，将问题中的几何关系转化为代数运算求解．

1．2 借一题多解，发散思维

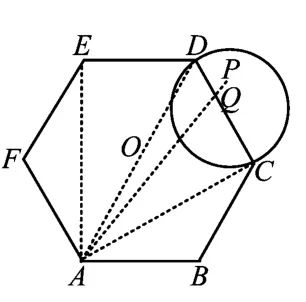
图5

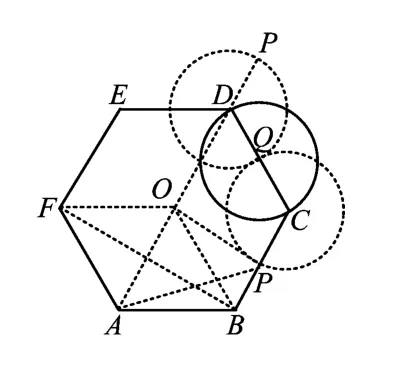
图6

解法2(共线向量定理)如图6所示，设O为正六边形的中心，则

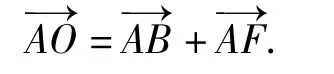
1)当动圆Q的圆心经过点C时，与边BC交于点P，点P为边BC的中点，联结OP，则

解法3(线性规划)以正六边形的顶点A为坐标原点、AB为x轴、AE为y轴建立直角坐标系．设 P(x，y)，易得

令m+n=z，画出点P满足的平面区域，易得m+n的取值范围是［2，5］．

解法4(参数方程)建立同解法3的平面直角坐标系，易得

点评此题解法颇多，是一道提高学生解题能力、拓展学生思维能力以及值得开发利用的好题．依据学生已有的实际认知水平，教师要引导学生进行反思探究，启迪学生思维，引发解题创新．在多种解法的探究中，不仅能让学生体验探索的快乐，而且能使学生加深对问题的认识．

2 几点思考

2．1 在交流探究中暴露学生的思维过程

叶澜教授曾说:“课堂是向未知方向挺进的旅程，随时都有可能发现意外的通道和美丽的因素，而不是一切都必须遵循固定路线而没有激情的行程．”课堂教学过程是复杂的、丰富多变的，难免会遇到超出预设方案之外的新问题、新想法，教师应善待学生提出的“意外”问题，尊重学生的“话语权”，为学生营造一个敢于发表自己见解、勇于说出自己想法的平台，适时调整教学设计方案，为学生的“动态生成”腾出一片广阔的空间，并因势利导，借题“发挥”，提升复习效益．

2．2 在比较中优化学生的思维能力

只有比较才能辨别优劣，只有比较才能使学生掌握更适合自己的解法．一题多解就是在比较中进行的，其目的要明确:不是解法越多越好，而应该选择有助于提升学生思维能力、培养学生解题能力的解法．通过一题多解训练，可以优化学生的解题思路，从而达到快速找准解决问题的方法．因此，解法比较可以不断拓展学生的思维能力．

本文是江苏省“十二五”重点资助课题《提高高中生学习效能的策略研究》(项目号:2013JK10－Z067)的研究成果之一．