一种改进的全比特算法

刘诗涵,王可东

(北京航空航天大学宇航学院,北京 100191)



一种改进的全比特算法

刘诗涵,王可东

(北京航空航天大学宇航学院,北京 100191)

摘要：提出一种改进的全比特算法。新算法将去载波后的信号进行块累加,将20 ms的相干积分缩短至1 ms,并采用FFT并行捕获,在不影响捕获灵敏度的前提下,大大降低了算法的运算量。利用归一化后最大相关值和次大相关值之差对捕获结果进行判决,提高了判决方法的适用性。最后,利用Matlab仿真的信号对算法进行验证,结果表明：利用20 ms的相干积分和5次非相干累加,能够捕获信噪比为-38 dB的微弱信号,执行时间缩短了近2/3.

关键词：全球定位系统;捕获;全比特;块累加

0引言

随着信息技术的飞速发展,人们对导航接收机的精度要求越来越高。现有的导航设备在正常环境下的定位精度已经基本满足要求,然而,室内、密集地区等复杂环境下的导航设备定位难以满足要求,究其原因,在于如此环境下GPS信号功率会大幅衰减,接收信号的载噪比严重恶化[1-2]。无辅助的GPS弱信号捕获需要更长的相干积分时间和更多的非相干积分次数来提高信号的载噪比,然而,导航数据比特只有20 ms,这将大大限制相干积分的长度。

传统的串行搜索算法首先对可见卫星进行搜索,然后在每颗可见卫星上的每一个可能的码相位和多普勒频移单元进行搜索,硬件上简单易实现,但捕获时间较长[3-4]。循环相关算法利用快速傅里叶变换(FFT)来加快信号处理速度,在弱信号捕获中主要靠延长累积时间来提高检测增益,但受导航比特跳转的限制[5-8]。半比特法和全比特法[9-10],有效的规避了数据比特跳变的影响,突破了相干积分时间20 ms的限制,但捕获速度较慢。文献[11]提出一种块累加方法,指出将多个1 ms数据在同一个采样点进行采样,采样得到的C/A码值不会改变,1 ms的采样数据就能覆盖整个码相位周期。文献[12]对块累加方法带来的信噪比提升进行了详细的分析,指出其在实际应用中仍会受到导航电文比特跳变的限制。

本文提出一种改进的全比特弱信号捕获算法。该算法通过块累加的方式,将全比特算法的20 ms相干积分缩短至1 ms,并采用FFT并行捕获,大大减少了运算量。仿真实验和分析表明,本文提出的算法有效可行,适用于GPS软件接收机,并且具有较高的运算效率。

1块累加法分析

对L ms的数据进行采样,将其分成L个数据块,每个数据块长度1 ms.假设1 ms的采样点数为N,则一共有NL个采样点,这里L≥1,且为整数。如图1所示。

图1L块采样数据

PRN为

k

的卫星的采样数据离散化后可以得到输入信号的复数表达形式:

sk(n)=Dk(nts)Ck(nts)ej2πfknts+vk(nts),

(1)

式中: ts=1/fs为采样周期; N ts=1ms; n∈[0,LN-1],Dk为导航数据位; Ck为C/A码; fk为带多普勒频移的载波频率; vk为高斯白噪声。

GPS每个导航数据位的长度是20ms,因此，

联系人： 刘诗涵E-mail:shihan_liu0815@126.com选取L≤20,并且认为在这L个数据块之内Dk(t)不变。

利用Ck(t)周期1ms的性质,可以得到

Ck(nts)=Ck[(n+N)ts],

(2)

式中: n=0,1,…,(L-1)N-1.

因此,对C/A码采样,不同数据块的相同位置采样数值一样。

本地载波NCO产生频率为Δfk的信号,记为lk(n)

lk(n)=ej2πΔfknts,

(3)

式中: n=0,1,…,(L-1)N-1.

将本地载波信号与输入信号相乘得到载波调整后的信号yk(n)

yk(n)=lk(n)·sk(n)

=Dk(nts)Ck(nts)

ej2π(fk+Δfk)nts+vk(nts)ej2πΔfknts.

(4)

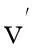
对yk(n)进行块累加,得到

=S{yk(n)}G(L,

(5)

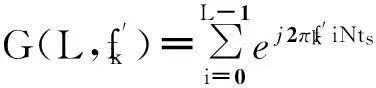
(6)

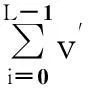
对长度为Lms的信号进行FFT并行捕获时,如果不对信号进行块累加,FFT的点数为NL个,对信号进行块累加后,FFT处理的点数降至L个,因此对信号进行块累加后,可以大幅降低后续捕获算法的计算量,提高算法的执行速度。

2改进的全比特弱信号捕获算法

为了克服导航数据比特20 ms的限制,Psiaki提出了全比特算法。全比特算法能够规避比特跳变的影响,将相干积分时间扩展至20 ms,有效提高信号载噪比,但是其需要对所有可能的跳变进行估计,亦即需要进行20组20 ms的相干积分,运算量很大。

按照前文的分析,本文利用块累加法对全比特算法进行改进。首先对输入的中频信号分成20组,然后将每组去载波后的20 ms数据进行块累加,成为1 ms的数据,接着采用基于FFT的循环相关方法,将码相位搜索并行化,最后将这20组数据分别进行非相干累加,查找最大相关峰值,进行捕获判决并输出结果。

本文提出的改进的全比特算法,将运算量很大的20 ms相干积分降低至1 ms相干积分,能够大幅降低算法的计算量,加快算法的捕获速度。算法的信号分组及算法框图如图2和图3所示。

图2　全比特算法信号分组图

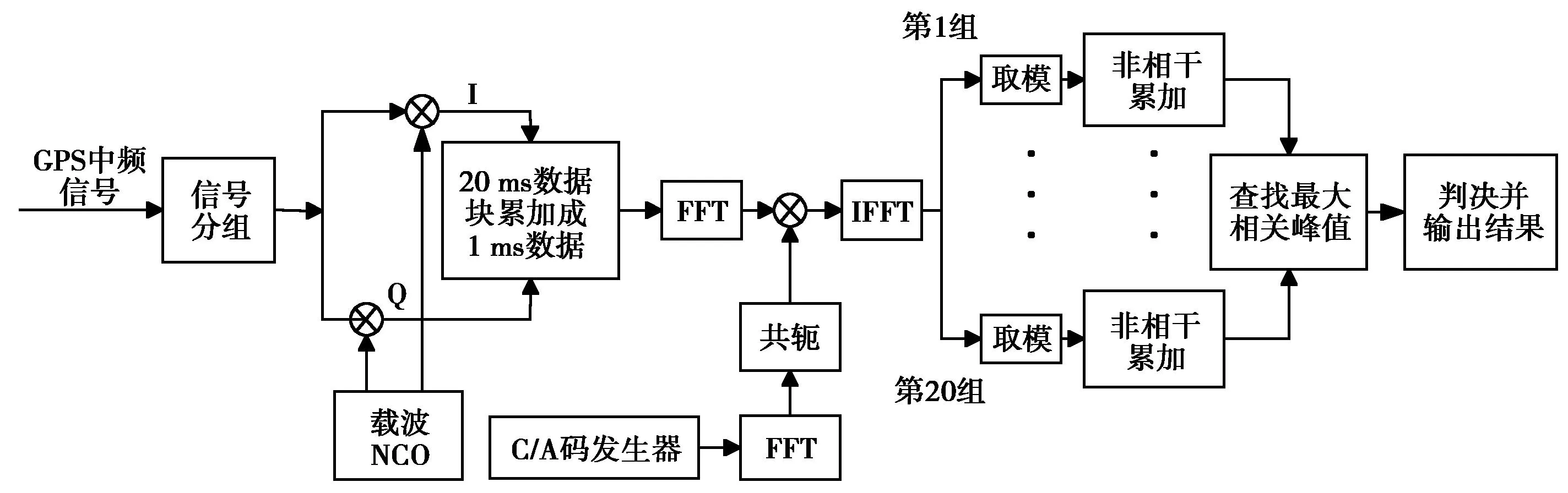
图3　改进的全比特算法框图

算法的具体实现过程如下:

1) 将输入信号按照图1进行分组,得到由M个20 ms数据块组成的20组数据。

2) 将分组后的信号分别与载波NCO输出的特定载波频偏的信号相乘,去除信号的载波分量。

3) 将载波分离后的20组数据中的每个20 ms的数据块分别进行累加运算,得到20×M个长度为1 ms的数据。

4) 分别对每组1 ms的数据进行FFT,并将FFT结果分别与本地C/A码的共轭FFT相乘,对相乘结果进行快速傅里叶反变换。

5) 将每组数据的结果进行取模运算,然后进行M次非相干累加,得到20个相关峰值。

6) 保留20个峰值中最大的一个,并进行捕获判决,输出结果。

3捕获判决方法

常用的捕获判决方法基于恒虚警概率准则,利用噪声的统计特性,在某一检测概率下设定捕获阈值,如果捕获的相关峰值超过阈值,则判定捕获成功,否则认为捕获失败[15]。这种判决方法对于不同的环境并不通用,因为捕获前无法预知信号的载噪比。

文献[14]利用统计学相关理论推导了一种利用最大相关值与次大相关值之差确定捕获阈值的判决方法,本文参考这种判决方法,具体为

1) 找到相关值中最大相关值,次大相关值。

2) 将相关值归一化,即将所有相关值除以最大相关值,这样最大相关值归一化后的值为1,次大相关值归一化后的值为小于1的正数。

3) 如果归一化后,最大相关值-次大相关值>0.15,则认为捕获成功,否则认为捕获失败。

4算法增益分析

改进的全比特算法利用相干积分和非相干积分来提高信号的处理增益,增益的具体计算方法如下:

相干积分所获得的增益Gc为[15]

Gc=10×lgTcoh,

(7)

式中:Tcoh为相对于1ms的数据长度。

非相干积分所获得的增益Gnc为[15]

Gnc=10×lgNnc-L(n),

(8)

式中: Nnc为非相干积分的数目; L(n)为非相干积分损耗。

非相干积分的损耗为[15]

(9)

式中: n为非相干积分数目,Dc(1)为在特定虚警概率和检测概率下的理想检测因子。这里取虚警概率为10e-7,检测概率为0.9,此时Dc(1)≈21[13]。

5实验验证

仿真试验要达到以下两个目的:

1) 验证本文提出的改进的全比特算法不会造成捕获灵敏度的降低。

2) 验证本文提出的算法较传统的全比特算法复杂度得到了降低,运行效率得到了提升。

本文的仿真数据用Matlab生成,中频频率为4.123 968 MHz,采样频率为16.367 667 MHz.

本文选取5段连续的20 ms数据进行验证,利用式7、8、9可以计算本文提出的改进的全比特算法所能获得的捕获增益为

G=Gc+Gnc=10×lgTcoh+10×lgNnc-

=19 dB,

式中:Tcoh=20;Nnc=n=5,Dc(1)≈21.

GPS信号的标称信噪比为-19 dB,按照上述增益计算,基于本文提出的算法对100 ms长度的数据进行处理,理论上能够捕获信噪比为-38 dB的信号,下面对本文提出的算法进行验证。

仿真生成12号卫星的信噪比为-38 dB的信号,图4示出了基于本文提出的算法的捕获结果。图4显示有明显的相关峰存在,图5显示归一化的最大值与次大值之差为0.43,超过捕获阈值0.15,因此捕获成功,本文提出的算法有效可行。

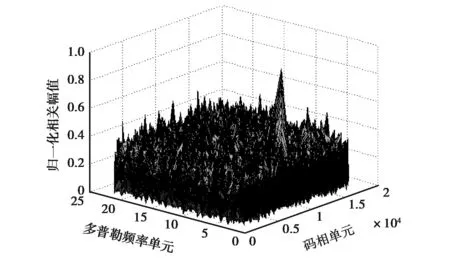
图4　12号卫星捕获结果

图5　12号卫星码相位捕获细化图

对未改进的全比特算法和改进后的全比特算法分别进行上机测试,对比二者的运行时间,所用PC机的配置为Inter Core i5-3470@3.20 GHz处理器,内存4 GB,改进前后的处理时间对比如表1所示。由表1可见,改进后的全比特算法,在不影响捕获灵敏度的前提下,运行时间缩短近2/3,运算复杂度大大降低。

表1　改进前后算法执行时间对比

6结束语

本文提出了一种改进的全比特算法,利用块累加和FFT技术将传统的全比特算法的20录ms相干积分缩短至1 ms,并采用循环相关的方法进行并行捕获。实验结果表明,通过20 ms的相干积分并进行5 次非相干累加,改进后的算法能够捕获到信噪比为-38 dB的GPS 信号,灵敏度并未受到影响,而且改进后的算法,其运行时间较传统的全比特算法缩短了近2/3。因此,本文提出的改进算法能够大大减少计算量,为弱信号捕获算法用于工程实际提供参考。

参考文献

[1] RODRIGUEZ J A A, EISSFELLER B. Theory on acquisition algorithms for indoor positioning[C]//12th Saint Petersburg International Conference on integrated navigation systems. 2005.

[2] ZHU C, FAN X. GNSS Signal acquisition in weak signal condition[C]//Communication Systems, Networks & Digital Signal Processing (CSNDSP), 2014 9th International Symposium on. IEEE, 2014: 1128-1132.

[3] PARKINSON B W. Progress in astronautics and aeronautics: global positioning system: Theory and Applications[M]. AIAA, 1996.

[4] MISRA P, ENGE P. Global positioning system: signals, measurements and performance Second edition[M]. Lincoln, MA: Ganga-Jamuna Press, 2006.

[5] 徐晓苏, 范金洋. GPS 软件接收机捕获算法[J]. 中国惯性技术学报, 2009, 17(2): 165-169.

[6] TSUI J B Y. Fundamentals of global positioning system receivers[M]. Wiley-Interscience, 2000.

[7] VAN NEE D J R, Coenen A. new fast GPS code-acquisition technique using FFT[J]. Electronics Letters, 1991, 27(2): 158-160.

[8] STARZYK J A, ZHU Z. Averaging correlation for C/A code acquisition and tracking in frequency domain[C]//Proc. IEEE Midwest Sym. on Circuits and Systems (MWSCAS), 2001(2): 905-908.

[9] PSIAKI M L. Block acquisition of weak GPS signals in a software receiver[C]//ION GPS. Salt Lake City, 2001：2838-2840.

[10]LIN D M, TSUI J B Y. Comparison of acquisition methods for software GPS receiver[C]//Proceedings of the 13th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GPS 2000), 2000: 2385-2390.

[11]HECKLER G W, GARRISON J L. Experimental tests of unaided weak signal acquisition methods using a software receiver[C]//Proceedings of the 19th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2006). 2001: 1309-1320.

[12]鲁郁.GPS全球定位接收机-原理与软件实现[M].北京:电子工业出版社,2009.

[13]LACHAPELLE G. Software receiver strategies for the acquisition and re-acquisition of weak GPS signals[C]//ION NTM, 2008.

[14]MAO W L, CHEN A B. New code delay compensation algorithm for weak GPS signal acquisition [J]. AEU-International Journal of Electronics and Communications, 2009, 63(8): 665-677.

[15]李寅寅, 徐晓苏, 刘锡祥. 基于半比特交替和 FFT 组合的 GPS 软件接收机弱信号捕获算法[J]. 中国惯性技术学报, 2012, 20(1): 46-50.

刘诗涵(1989-),男,河南商丘人,硕士生,主要从事卫星导航和组合导航相关研究。

王可东(1975-),男,安徽庐江人,博士,副教授,主要从事飞行器导航、制导与控制、惯性导航仪器、匹配算法、卫星导航等方向的研究。

An Improved Full-Bit Algorithm

LIU Shihan,WANG Kedong

(SchoolofAstronautics,BeihangUniversity,Beijing100191,China)

Abstract:An improved full-bit algorithm is proposed. The new algorithm uses block addition upon the carrier-removed signal and shortens the 20ms coherent integration to 1ms.After that, the signal is captured in a parallel way-FFT. The improved algorithm reduces the computing amount greatly with acquisition sensitivity unreduced. Acquisition results are judged by the difference between the normalized maximum value and second maximum value of autocorrelation. This method improves the applicability of acquisition judgment. At last, the improved algorithm is verified with simulated GPS signal in Matlab. Simulation results indicate that weak GPS signals with SNR of-38 dB can be captured through 20 ms coherent integration and 5 times of non-coherent integration, and the executing time is reduced by about 2/3 compared with the former algorithm.

Key words:GPS; acquisition; full-bit; block addition

作者简介

收稿日期：2015-06-10

中图分类号：V19;TP391

文献标志码：A

文章编号：1008-9268(2015)06-0011-05

doi:10.13442/j.gnss.1008-9268.2015.06.003