基于BP神经网络的伪距观测值电离层误差分离

李阳林,黄文德,盛利元

(1.中南大学物理与电子学院,长沙 410083;

2.国防科技大学机电工程与自动化学院,长沙 410073)



基于BP神经网络的伪距观测值电离层误差分离

李阳林1,2,黄文德2,盛利元1

(1.中南大学物理与电子学院,长沙 410083;

2.国防科技大学机电工程与自动化学院,长沙 410073)

摘要：针对单频接收机用户伪距观测值中电离层延迟误差分离难的问题,提出了基于BP神经网络的误差分离方法，以接收机连续一周的观测数据作为训练样本,将样本中时间、卫星高度角、方位角及伪距观测值作为BP神经网络的输入单元,利用CODE提供的高精度GIM计算出对应的电离层延迟误差,并将其作为输出单元对BP神经网络进行训练。最后,利用训练好的模型对接下来一周各可见星伪距观测值的电离层延迟误差进行分离。实例表明:利用BP神经网络模型对伪距观测值的电离层延迟误差进行分离,分离精度均在80%以上,最佳可达90%.该方法是从大数据的角度解决导航问题的一次有益尝试。

关键词：BP神经网络;单频接收机;伪距;电离层延迟误差

0引言

电离层延迟误差是卫星导航定位系统中的主要误差源之一[1-2]，目前,解决电离层延迟误差的方法主要有:双频改正法和电离层模型法。双频改正法主要根据电离层时延效应与信号频率平方呈反比的关系,直接利用双频组合的方式计算得到电离层时延,适用于双频接收机用户。而双频接收机价格较为昂贵,市面上使用较多的是单频接收机。单频接收机用户只能接收到单频伪距观测值,通常需采用有效的电离层延迟模型来削弱电离层时延的影响。目前,全球定位系统(GPS)导航电文中采用的电离层模型为Klobuchar模型，Klobuchar模型结构简单,计算方便,但总体精度不高,其全球改正精度约为50%～60%[3]。

伪距观测值中电离层延迟误差的影响因素较多,是个复杂的非线性系统。人工神经网络(ANN)可以模拟人的大脑神经处理信息方式,能够比较轻松地实现非线性映射过程,且具有大规模的计算能力,解决了很多利用传统方法难以解决的问题[4]。近年来,神经网络已经广泛应用于电离层短期预报研究及测站天顶方向总电子含量(VTEC)的预报等[5-8]研究,但将神经网络用于单频接收机伪距观测值中电离层延迟误差分离的研究较少。

反向传播神经网络(BPNN)是一种经典的ANN算法,具有很强的非线性动态处理能力,能够较好地表达各输入与输出的隐式非线性对应关系[9-10]。本文根据国际地球动力服务组织(IGS)的欧洲定轨中心(CODE)提供的高精度全球电离层图(GIM)计算出伪距观测值中的电离层延迟误差,提出利用BP神经网络对单频接收机伪距观测值的电离层延迟误差进行分离的方法，并结合实例,将分离所得电离层延迟误差与利用GIM计算得到的高精度电离层延迟误差进行比对,验证了该方法的可行性和有效性。

1伪距中的电离层延迟误差

电离层分布于地球表面以上60～1 000 km的空间,是一种弥散性介质。电离层中的大气分子在太阳光的照射下会分解成大气离子和电子,卫星导航信号穿过充满电子的电离层时,会发生反射、折射、散射及吸收,使得信号路径产生弯曲且传播速度会发生变化。接收机伪距观测值中的电离层时延与电子总量成正比,与信号频率的平方成反比,以米为单位的电离层时延Iρ为

资助项目： 第二代卫星导航重大专项(编号:GFZX0301010105)

联系人： 李阳林 E-mail: li1008686@qq.com

(1)

式中: f为信号频率; Ne为单位面积的横截面在信号传播途径上所拦截的电子总量。

CODE每天根据IGS分布在全球约200个GPS/GLONASS测站和其它机构的数据,解算发布两种GIM。GIM产品给出时间间隔为2 h,地理纬度范围为87.5°S~87.5°N,分辨率为2.5°;地理经度范围为180°W～180°E,分辨率为5°的电离层VTEC分布[11]。其中一种是每天的快速解,推迟一天发布,命名为CORG文件;一种是综合了若干个VTEC归算中心的结果得到的综合解,一般推迟五天发布,命名为CODG文件。IGS发布的CODG文件时间精度合适,数据可靠性高,可将其视为实测VTEC值,且利用格网电离层模型内插可计算出任意穿刺点的VTEC值。此外,根据VTEC可计算得到Ne,即利用IGS提供的VTEC值对电离层延迟误差分离效果进行评定具有很好的客观性。Ne与VTEC的关系为

(2)

式中:VTEC为电离层穿刺点处的垂直电子总含量;θ为穿刺点处的天顶角。

2基于BP神经网络的电离层误差分离模型

2.1BP神经网络基本原理

BP神经网络是人工神经网络中最重要的网络之一,体现了人工神经网络的精华,其本质是以网络误差的平方和为目标函数,按梯度下降算法求其目标函数达到最小值的算法。根据Kolmogorov定理,对于任何一个闭区间内的连续函数都可以用单隐层的BP网络逼近,即一个三层BP神经网络就可以完成任意的N维到M维的映射,其拓扑结构如图1所示。

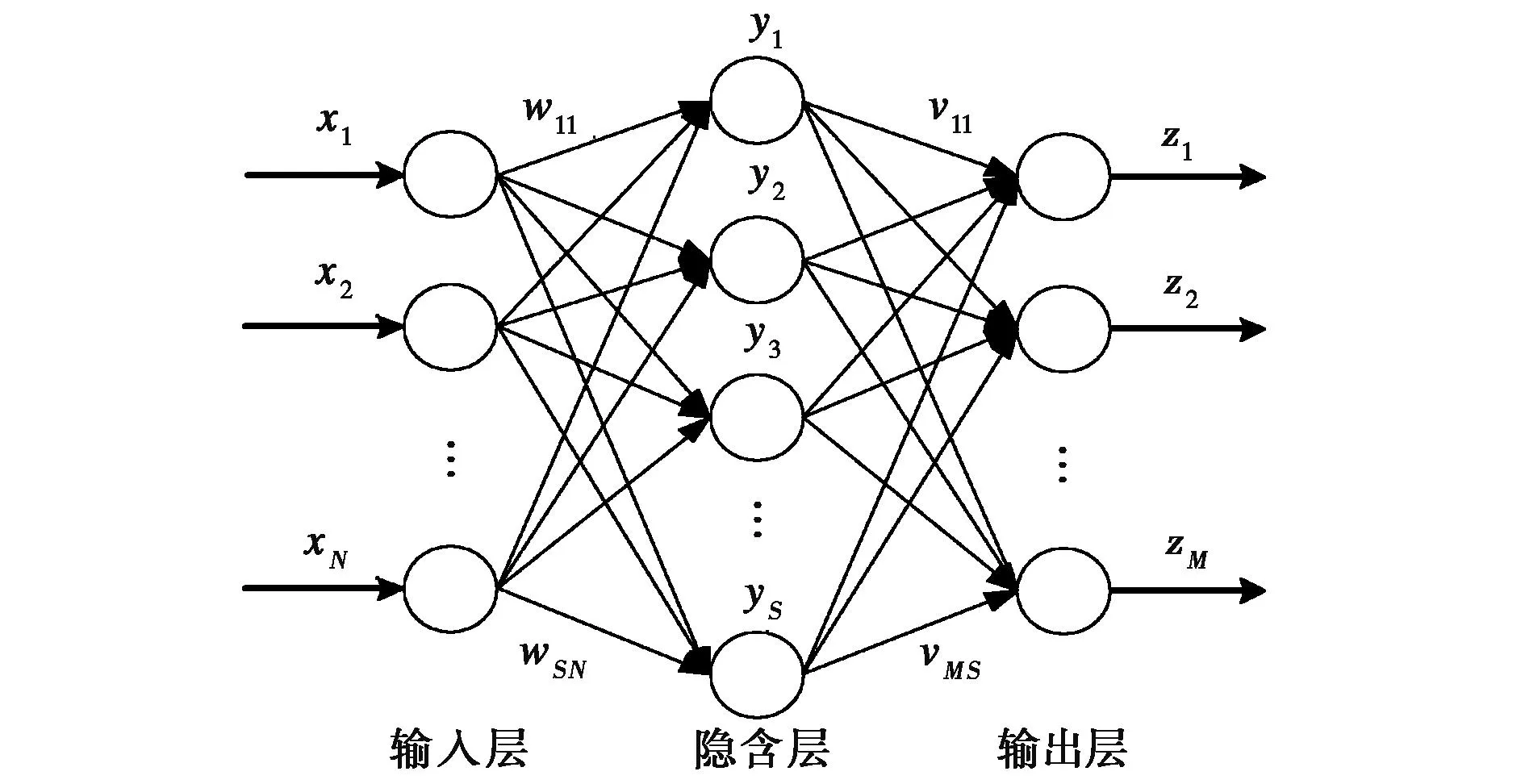
图1　3层BP神经网络拓扑结构图

设BP神经网络的输入向量X=(x1,x2,…,xN),N为输入分量的个数;隐含层神经元个数为S,其输出向量为Y=(y1,y2,…,yS);输出层输出向量为Z=(z1,z2,…,zM),M为输出分量的个数。输入层到隐含层的权值为{wji}(j=1,2,…,S;i=1,2,…,N),阈值为θj;隐含层到输出层的权值为{vkj}(k=1,2,…,M;j=1,2,…,S),阈值为γk,各输出节点的期望值为gk.该学习过程由信号的正向传播和误差的反向传播组成,主要计算步骤为

3) 根据误差E,修正权值wji和vkj、阈值θj和γk.

4) 判断误差E是否满足设定值,满足则结束训练,不满足则重复以上步骤。

2.2电离层误差分离模型输入因子确定

由式(1)和式(2)可知,单频接收机伪距观测值中电离层延迟误差主要由穿刺点处的天顶角和VTEC所决定，其中,天顶角可根据卫星高度角及方位角计算得出。影响电离层VTEC的因素很多,从短期来看,对于固定的时间点,电离层VTEC随穿刺点空间位置分布的不同而不同;对于固定的穿刺点,电离层VTEC随地方时具有明显的周日变化规律,约呈余弦曲线变化。为了增加电离层延迟误差分离的准确性,不同时段的BP神经网络模型应以不同时段的数据样本为训练样本,而在一个较短的时段内(如2h)电离层VTEC数据相对较为稳定,因此，用本文提出的方法进行伪距观测值电离层延迟误差的分离时,以2h为一个时段将一天24h分为12个时段。综上所述,本文利用3层BP神经网络来建立伪距观测值的电离层误差分离模型,选取时间、伪距、可见星高度角及方位角这4个和伪距观测值电离层误差分离相关性很大的因素作为神经网络的输入因子。

3算例分析

太少的隐含层神经元会导致网络“欠适配”,太多的隐含层神经元又会导致“过适配”,根据经验,本文选取隐含层节点数为10。基于以上分析,首先整理中国长春站(CHAN)2014年1月2号-2014年1月8号2～4h时段的观测数据,然后以30s为周期,根据各可见星播发的广播星历计算出相应的卫星位置,最后在此基础上计算整理出各颗卫星的可见时间(天内秒)、高度角、方位角及单频伪距值并将其作为学习输入;利用IGS提供的GIM进行插值计算得出以m为单位的单频伪距值的电离层时延I作为输入目标对BP神经网络进行训练。其中,隐含层和输出层均采用tansig型激活函数;BP网络的学习算法采用Levenberg-Marquardt算法;权值和阈值的BP学习算法为learngdm;网络的性能函数采用mse;设置最小均方误差为0.001;学习速率为0.05;且所有数据均利用premnmx函数将其归一化到-1～1。

对BP神经网络进行训练收敛之后,对CHAN2014年1月9日至1月15号2～4h时段的伪距进行电离层延迟误差分离。以根据IGS提供的VTEC综合解计算得出的电离层时延I为真实值,真实值与基于BP神经网络所得分离值之差为分离残差。本文利用分离残差的平均值、均方差和误差改正精度来对分离效果进行评价，其中误差改正精度v的计算公式为

(3)

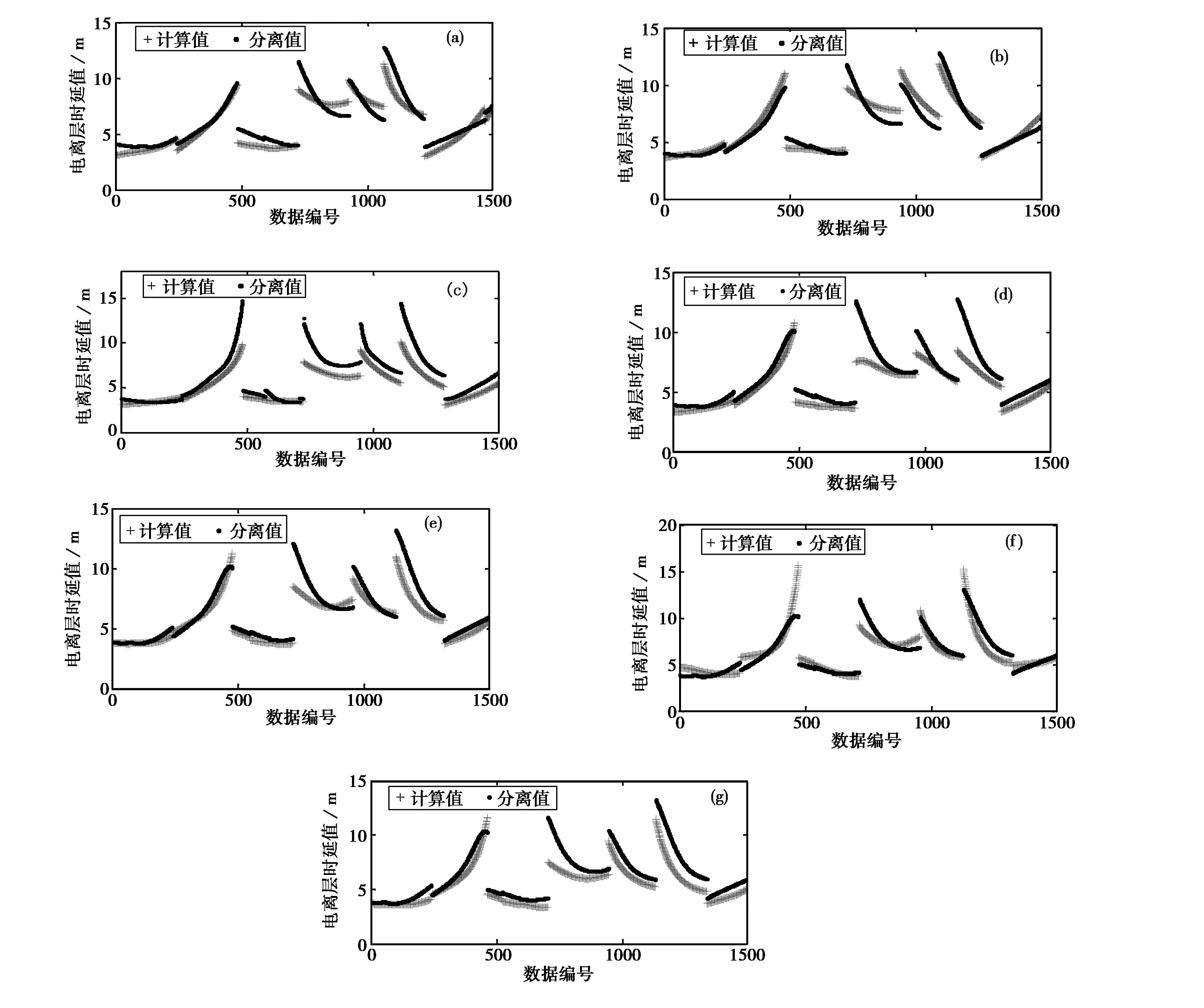
图2　基于BP神经网络的电离层误差分离值2014年(a)1月9日; (b)1月10日; (c)1月11日;(d)1月12日; (e)1月13日; (f)1月14日; (g)1月15日

式中:I分离值为利用本文所提方法得出的电离层时延;I真实值为利用实测VTEC计算得到的电离层时延。考虑到篇幅所限,本文只给出接收机前1 500个伪距数据的分离结果,如图2和表1所示。

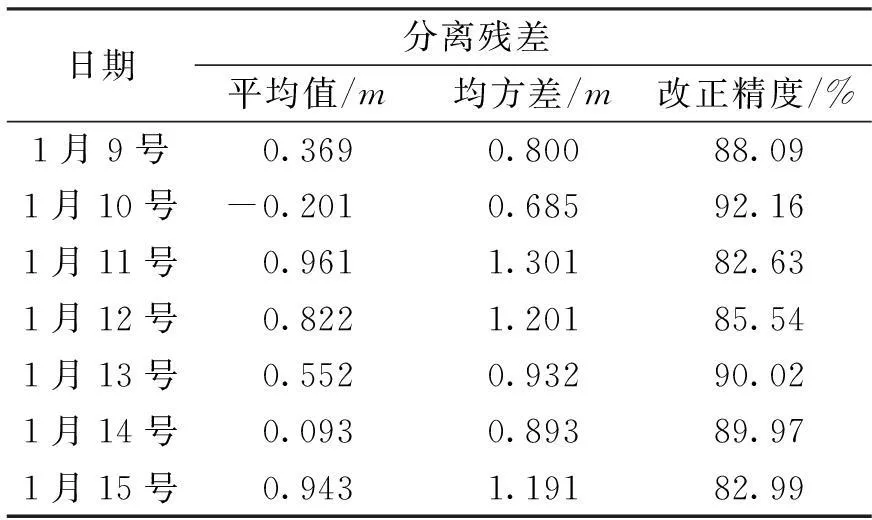
表1　1月9号-1月15号的分离误差统计

分析图2和表1可知,利用一周的实际数据对BP神经网络模型进行训练,应用训练后的模型对接下来一周时间内的伪距观测值进行电离层延迟误差分离,能够很好的反应各卫星伪距观测值中电离层延迟误差的变化趋势,总体来说效果较佳。且一周之内,最差的改正精度为82.63%,最优的改正精度可达92.16%。该方法的关键在于获取历史的实测电离层延迟误差值,而IGS给出的全球电离层图精度高,可以通过插值算出全球任意点的VTEC值。本文提出的电离层延迟误差分离方法很好的利用了大量较为精确的历史实测数据。实例分析表明,利用该方法可以同时对大批量数据进行处理,且分离效果好,改正精度高。

4结束语

针对单频接收机电离层延迟误差分离难的问题,本文将BP神经网络应用于单频接收机伪距观测值电离层延迟误差的分离中。以时间、卫星高度角、方位角、伪距作为电离层延迟误差的相关因素,提出了基于BP神经网络的电离层延迟误差分离模型。实例分析表明,一周以内伪距观测值电离层误差的改正精度最差为82.63%,最优为92.16%。因此,该方法充分利用了BP神经网络的泛化能力,在不需要硬件支持的基础上实现了电离层延迟误差的分离,且所得模型比常规经验模型效果更好,初步验证了利用BP神经网络进行电离层延迟误差分离的可行性和有效性。本文所作的研究,尚未考虑发生强烈电离层变化如电离层暴等时的情况,仅是对正常情况下伪距观测值电离层延迟误差分离的初步探讨,所用方法尚待改进与完善。

致谢：感谢IGS提供的GPS数据。

参考文献

[1] 李耿浩, 赵梦琪. 北斗系统电离层模型参数改正精度分析[J].全球定位系统,2014,39(5):79-81.

[2] 谢钢.GPS原理与接收机设计[M].北京:电子工业出版社, 2009.

[3] 王斐, 吴晓莉, 周田, 等.不同Klobuchar模型参数的性能比较[J].测绘学报,2014,43(11):1151-1157.

[4] 葛哲学, 孙志强. 神经网络理论与MATLABR2007实现[M].北京:电子工业出版社, 2007.

[5] 陈丹俊, 吴健, 王先义. 电离层暴时的foF2预报技术研究[J].地球物理学报, 2007,50(1):18-23.

[6]HABARULEMAJB,MCKINNELLLA,CILLIERSPJ.Predictionofglobalpositioningsystemtotalelectroncontentusingneuralnetworksoversouthafrica[J].JournalofAtmosphericandSolar-TerrestrialPhysics.2007(69): 1842-1850.

[7]MCKINNELLLA,FRIEDRICHM.Aneuralnetwork-basedionosphericmodelfortheauroralzone[J].JournalofAtmosphericandSolar-TerrestrialPhysics. 2007(69):1203-1210.

[8]FRIEDRICHM,EGGERG,MCKINNELLLA, et al.PerturbationsinEISCATelectrondensitiesvisualisedbynormalisation[J].AdvancesinSpaceResearch. 2006(38):2413-2417.

[9] 范国清, 王威, 郗晓宁. 基于广义回归神经网络的电离层VTEC建模[J]. 测绘学报, 2010, 39(1):16-21.

[10]陈帅, 朱小玉, 王鹏,等. 回归分析和BP神经网络在地表沉降监测中的应用[J]. 全球定位系统, 2012, 37(1):92-94.

[11]尹光志, 李铭辉, 李文璞,等. 基于改进BP神经网络的煤体瓦斯渗透率预测模型[J]. 煤炭学报, 2013, 38(7):1179-1184.

[12]HERNANDEZ-PAJARESM,JUANJM,SANZJ, et al.TheIGSVTECmaps:Areliablesourceofionosphericinformationsince1998[J].JournalofGeodesy. 2009, 83(11):263-275.

李阳林(1991-),女,硕士生,主要从事卫星导航仿真系统及观测数据处理研究。

黄文德(1981-),男,博士,讲师,主要从事航天器轨道动力学及卫星导航系统技术研究。

盛利元(1956-),男,教授,硕士生导师,主要研究领域为非线性系统与混沌加密理论。

Pseudo-range Observations Ionospheric Error

Separation Based on BP Neural Network

LI Yanglin1,2,HUANG Wende2,SHENG Liyuan1

(1.CollegeofPhysicandElectronic,CentralSouthUniversity,Changsha410083,China;

2.CollegeofMechatronicsEngineeringandAutomation,NationalUniversityof

DefenseTechnology,Changsha410073,China)

Abstract:Aiming at the problem of ionospheric delay error, proposed a new error separation method based on BP neural network. The training sample is based on a week of observation data and set the pseudo-distance ionospheric delay error separation-related factors-time, satellite elevation angle, azimuth and pseudo-range observations as BP neural network input unit, use CODE published high-precision GIM calculated corresponding ionospheric delay error as an output unit for BP neural network training. Finally, use the trained model for each satellite to separate next week ionospheric delay error of pseudorange observations. The results show that: the use of BP neural network model to separate ionospheric delay error of pseudo-range observations, both of the separation accurate is above 80%, and the best is up to 90%. The method used a large number of actual historical data, it is a good attempt to solve navigation problems from the perspective of big data.

Key words:BP neural network; single-frequency receivers; pseudorange; ionospheric delay error

作者简介

收稿日期：2015-09-06

中图分类号：P228.4

文献标志码：A

文章编号：1008-9268(2015)06-0001-05

doi:10.13442/j.gnss.1008-9268.2015.06.001